Detecting Math-and-ICT Competence

Maria Shabanova

and Borislav Lazarov

Institute of Mathematics, Information and Space Technologies, M. Lomonosov Northern (Arctic) Federal University,

Arkhangelsk, Russia

Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Soﬁa, Bulgaria

Keywords:

Socratic Style, Dynamic Geometry Software, Van Hiele’s Level, Synthetic Competence.

Abstract:

Theoretically DGS (dynamic geometry software) environment allows developing students’ critical thinking

via discovering some properties of the ﬁgures by exploring DGS applets. Our goal is to examine how this

theory works in teaching a new non-trivial geometry concept. We study which van Hiele’s level of geometrical

reasoning is covered by the students in two cases. The ﬁrst testing group worked in Socratic style of teaching

without any time limit. The second one was restricted to the regular classroom parameters and the teacher

applied instructional mode of teaching. The topic is the introduction of a new locus not included in the

standard curriculum but in the students’ zone of proximal development. We are interested in the transition

of knowledge and skills developed in paper-and-pencil context to the DGS environment. The transition we

consider as an indicator of competence of synthetic type. As the outcomes of the study, some important details

of incorporating DGS in teaching-learning process in secondary school were clariﬁed.

1 INTRODUCTION

The last pan European initiatives to modernize the

secondary school math education refer to so called in-

quiry based education (Rocard et al., 2007). Key role

in the change of the paradigm play the outcomes of

the SINUS and SINUS-Transfer projects held in Ger-

many (Baptist et al., 2011) where the Dynamic Work-

sheets done in dynamic geometry software (DGS) en-

vironment occupied the central location in teaching-

learning process.

Meanwhile several initiatives to organize more at-

tractive and effective math education based on DGS

educational environment are taking place in the Rus-

sian Federation (Shabanovaet al., 2013). One of them

is with cooperation of Bulgarian Institute of Mathe-

matics and Informatics in the frame of the MITE (Me-

thodic and Information Technologies in Education)

project and it aims to design educational resources

and to prepare staff for implementation of these re-

sources in regular practice (see Note 1).

In general the goal of these movements is the re-

quirements of the key-competences deﬁned in (Eu-

ropean Commission, 2004) to be covered after the

compulsory education (whatever it means). We adopt

the main idea of the key-competence-deﬁnition that

a key-competence should be a transferable, multi-

functional package of knowledge, skills and attitudes

(ibid.) Building such kind of packages separately for

any particular school subject reduces both its trans-

ferability and multifunctionality,this is why we advo-

cate considering the competence as a synthetic con-

cept (Lazarov, 2013). The study we present in this pa-

per is an attempt to clarify some parameters of incor-

porating DGS in the regular teaching-learning prac-

tice aimed to make possible the transfer of knowledge

and skills in a new context (decontextualization) (see

Note 2). More speciﬁcally - we are interested in the

level of transferability and multifunctionality of some

knowledge and skills elaborated in paper-and-pencil

technique into DGS environment and the potential ad-

vantages that this provides for heuristics and thus for

inquiry based approach of teaching-learning.

2 METHOD AND OBJECTIVES

We consider the theory of Van Hieles level of geomet-

rical reasoning (VanHiele, 1984) as the most relevant

for describing the student’s progress in building a new

geometrical concept (a short description of the lev-

els is given in the Appendix). It is important for our

purpose the minimal initial van Hiele’s level of rea-

soning to be determined as either 3 or 4. The level 3

153

Shabanova M. and Lazarov B..

Detecting Math-and-ICT Competence.

DOI: 10.5220/0004840401530158

In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 153-158

ISBN: 978-989-758-021-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

guaranties that the student can use DGS as an educa-

tional tool but not (only) for fun. Level 4 we accept as

the desired educational goal in the secondary school.

Our standing point is that a student has built the math-

and-ICTcomponent on a competence of synthetic type

when (s)he is able to apply DGS for solving new non-

trivial problems. This is of course in the context of

the high secondary school mathematics curriculum

(grade 8 and up). Since the education in geometry

is based on the traditional paper-and-pencil method-

ology the ability to present knowledge and skills in

DGS format properly ensures their transferability and

multifunctionality, i.e. the presence of a competence.

The objectives we stated were to examine the ex-

istence or lack of transfer of KSA (which indicates a

kind of competence) and to clarify the time needed

for elaborating a new concept applying inquiry-based

style of teaching-learning. We investigate the reason-

ing of a new which locus, is close to the basic core

of the curriculum but also requires the transfer of the

KSA in a non-trivial way. We adopt the following in-

dicators of detecting such kind of competence:

I1. Proper idea about the locus and design of a

proper DGS instrument.

I2. The construction is explored and the conjec-

ture is supported by examples; the statement is stated

and proved.

I3. Ability for independent work and the level of

the teacher’s intervention.

We integrate the DGS interface with the common geo-

metrical language of the van Hiele’s level 3, forming a

kind of metalanguage. It allows more effective com-

munication during the lesson but also more reliable

observation on the indicators. For instance measuring

the transfer of KSA includes the stability of a partic-

ular DGS construction. Meanwhile we keep an eye

on the student’s zones of actual and proximal devel-

opment (Vygotsky, 1935) when we evaluate his/her

progress.

Data collection was done during and after the les-

son: we gathered the sheets and the ﬁles of the stu-

dents; a video record of the lessons was made. How-

ever we also used the teacher’s observation on each

student in a longer period to clarify the van Hiele’s

level reached in similar matter.

3 TECHNICAL PARAMETERS

3.1 Population

Our target group was 9th grade students of an ordi-

nary school. We organized the experiment in two

groups: the ﬁrst one of 14 students and the second

of nine. All of them were familiar with GeoGebra

(they had more than 3 years experience in applying

it). The ﬁrst group is a regular class; the second group

is formed by students attending a math circle.

3.2 Teachers

The teachers involved in the study were among the

best math teachers, experts in inquiry-based educa-

tion, authors of the textbooks and having both deep

math knowledge and excellent skills in GeoGebra.

3.3 Problems

We designed two problems for the study. Problem

1. Find the locus of points inside a quadrilateral with

minimal sum of the distances to the lines containing

its sides. Investigate the case:

a) square;

b) rhombus;

c) parallelogram.

Problem 2. Find the locus of points inside a quadri-

lateral with minimal sum of the distances to its sides.

Investigate the case:

d) square;

e) rhombus;

f) parallelogram.

Students were expected to pass through the fol-

lowing steps:

step 1: the locus is drawn correctly,

step 2: the conjecture is relevant,

step 3: the conjecture is conﬁrmed by examples,

step 4: a proof is made,

step 5 (in Problem 1): a general proof for the

square, the rhombu and the parallelogram is made,

step 5 (in Problem 2): some particular shapes of

the locus are examined,

step 6 (in Problem 2): a new problem is stated and

solved.

3.4 Lesson Plan

Our experiment was held in a regular lesson (2 h 45

minutes) with the second group and an extended les-

son without time limit with the ﬁrst group (2 h 24

min). Both lessons followed the next plan

(1) Declaring the objectives of the lesson

(2) Reminding some basic facts

(3) Stating Problem 1 and the type of the activities

(4) Individual work on Problem 1

(5) Solving Problem 1 with tutoring

(6) Plenary discussion on Problem 1

(7) Elaborating basic knowledge and skills for

Problem 2

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

154

(8) Stating Problem 2

(9) Individual work on Problem 2

(10) Solving Problem 2 with tutoring

(11) Plenary discussion on Problem 2

(12) Drawing conclusions

Let us note that the concept of distance between point

and segment is not introduced in the curriculum. This

is why the students were given in advance a home-

work to elaborate the locus of points at given distance

from a segment. The homework includes also prob-

lems about the sum of the distances to two parallel

segments. The solutions were expected to be written

in traditional paper-and-pencil style.

3.5 Benchmarks

The coverage of the indicators was registered as fol-

lows.

I1. The ability to construct a dynamically stable

quadrilateral; the examined segments are dynamically

stable; the sum of the segments is explicitly noted.

I2. Progress in the solution of the problems about

the square, rhombus and parallelogram: the student

gives argumentsthat support the conclusions up to the

rigor proof.

I3. The student works independently or (s)he

manage to obtain the required results after teacher’s

reinforcement.

4 LESSON FLOW

The lessons started with a brief review of the home-

work. For us it was a check of the initial level of rea-

soning of the new concept: distance between point

and segment. Students performed some experimental

work with the ready applets. This introductory part

showed that in the both groups the DGS language was

properly learned.

There were advanced students from Group 1 who

managed to perform the standard questions quickly.

After doing this, they went further and deeper in the

solution of the problems. The unlimited time for indi-

vidual work did not give any advantages to the others.

As a rule, the teacher was more interested in the per-

formance of the advanced students. She performed

an individual Socratic inquiry with some of them if

needed. After some time the rest of the class was

given ready applets (Figure 1) provided with some

short instructions.

Students of the second group were given ready ap-

plets and clear instructions what to do. This approach

allowed more uniform movement along the lesson.

Moreover, the teacher had direct view on the transfer

Figure 1: The main experimental applet prepared by the

teacher in advance.

of the student’s knowledge build in paper-and-pencil

mode to the DGS environment. As soon as students

performed the experimental work, she went to the

proof of the results.

Very important parts of the lesson in both groups

were the plenary discussions when the students pre-

sented their ideas to the class. We detected the com-

petence level (or lack of competence) of any partic-

ular student more clearly during these discussions.

The use of the metalanguage (natural language +

math expressions and drawings completed with DGS-

interface notation – see Note 3) allowed students to

support their arguments better. We consider the abil-

ity to use properly such style of communication as

existence of some synthetic competence.

5 EXAMPLES

In this section, we present our observations on 3 stu-

dents. The ﬁrst two are the marginal cases in Group

1: the most advanced student and the one with modest

abilities. The third student is from the more homoge-

neous Group 2.

Figure 2: The only DGS construction designed by StudentI

during the lesson.

StudentI (Group 1). StudentI’s geometrical rea-

soning was classiﬁed by his teacher as van Hiele’s

level 4 for the most topics. StudentI often has

nonstandard ideas and gives original solutions. He

skipped the ﬁrst problem as not interesting - he im-

mediately guessed that the sum of the distances to two

parallel lines remains the same for any point between

them which answers the question in Problem 1.

DetectingMath-and-ICTCompetence

155

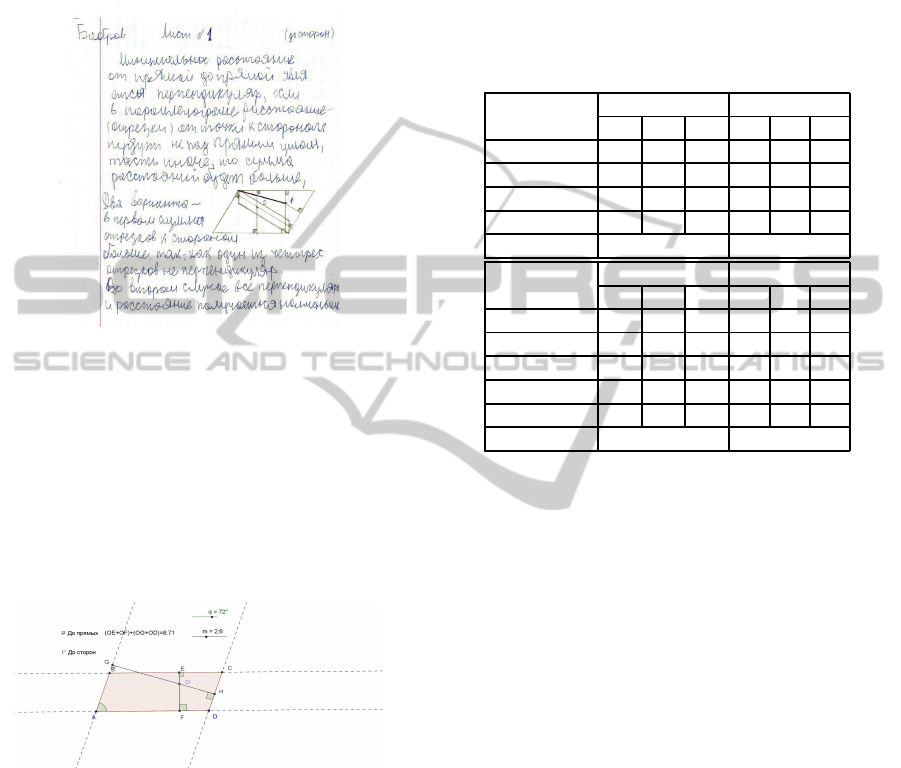
StudentI designed a single DGS construction (Fig-

ure 2) but it was enough to explore the locus in the

most general case. He passed the steps 1-3 in a very

short time and decided he is ready. After the teacher

urged him, StudentI passed step 4 - he proved the as-

sertion without any enthusiasm (Figure 3).

Figure 3: StudentI’s P& P ”proof”.

StudentG (Group 1). The teacher determines Stu-

dentG’s geometrical reasoning as van Hiele’s level

1, but even he managed passing step 1. Further, he

used the applet provided by the teacher. StudentG did

not show any progress in Problem 2 after the individ-

ual work in the DGS environment. He passed step

1 in Problem 2 after some explanations given by the

teacher. It seemed to be that Problem 2 is beyond the

StudentG’s zone of proximal development (ZPD).

Figure 4: DGS applet provided by the teacher to StudentG

with his explorations.

StudentA (Group 2). She was classiﬁed by her

teacher as reasoning in Van Hiele’s level 3. StudentA

had some experience in a kind of research activities.

She was expected to pass all steps independently. In-

stead of this she asked the teacher’s instructions all

the time. But she went further than the other students

exploring some more cases. She did not prefer paper-

and-pencil drawing and made her proofs using only

the DGS applets for supporting her intuition.

6 RESULTS

Table 1 represents the progress made by students in

solving the problems. The columns a), b), c) stand for

the parts of the Problem 1; the numbers in the rows

show how many students covered the corresponding

step of the solution. Analogous are the columns d), e)

and f).

Table 1: The progress in the solution.

Progress in Group 1 Group 2

Problem 1 a) b) c) a) b) c)

step 1 14 14 14 9 9 9

step 2 8 8 8 9 9 9

step 3 13 13 12 9 9 9

step 4 11 10 6 1 1 1

step 5 1 1

Progress in Group 1 Group 2

Problem 2 d) e) f) d) e) f)

step 1 14 14 14 8 8 8

step 2 13 13 13 8 8 8

step 3 13 13 13 8 8 8

step 4 9 9 8 2 2 2

step 5 0 0 2 0 0 1

step 6 1 0

We refer the steps 1 and 2 to the indicator I1. The

success in steps 3 and 4 is related to the indicator I2.

The time elapsed by the individual work or working

with tutoring on the problems is connected to the in-

dicator I3. These times were as follows:

Group 1.

Individual work on Problem 1 - 40 min.

Individual work on Problem 2 - 30 min.

Solving Problem 2 with tutoring - 17 min.

Group 2.

Solving Problem 1 with tutoring - 27 min.

Solving Problem 2 with tutoring - 17 min.

In our study we use the homework and Problem1

mainly to clarify the metalanguage in which students

were going to communicate in Problem 2. The data

collected clearly showed that the students were fa-

miliar with all needed auxiliary concepts when they

started solving the Problem 2. The homework and

Problem 1 played another important role for students

according to the inductive character of the van Hiele’s

level - the connections between the components of the

ﬁgures elaborated during solving these two prepara-

tory problems in paper-and-pencil mode (P&P) were

the necessary initial cognitive status for starting Prob-

lem 2. We give the observed van Hiele’s level (the

number of students who achieved the corresponding

level) in table 2.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

156

Table 2: The observed van Hiele’s level.

Van Hiele’s Group 1 Group 2

level P&P DGS P&P DGS

I 1 0 0 0

II 3 1 5 2

III 7 5 4 6

IV 3 8 0 2

7 FINAL REMARKS

We will skip advocating the obvious fact that the con-

text of paper-and-pencil is rather different from the

context of DGS environment and refer to (Marrades&

Gutierrez, 2000) for the review of the research of the

types of reasoning. We also agree with the ﬁndings

that rediscovering nontrivial math facts in classroom

practice is impossible even with most advanced stu-

dents (Lazarov&Sharkova,2013). So we are trying to

evaluate a signiﬁcant part of the total price that should

be paid for incorporating DGS in regular teaching

practice - namely the time elapsed for considerable

progress in studying a new math concept. Further, af-

ter paying the price, do we get the expected quality of

the educational product - the competence?

The statistics from table 1 clearly shows that the

ﬁrst indicator is covered by the students (with only

one exception) for the most trivial case. The conclu-

sion is that the students ”speak the DGS language ﬂu-

ently”. There is full-scale transition of the basic con-

cepts from the paper-and-pencil context to the DGS

environment. In some intuitive level students feel the

matter.

The poor performance in deduction shows that the

DGS abilities have little impact on the deeper under-

standing of the matter. This is not a big surprise if

we take into account that the deductive justiﬁcation is

characterized by the decontextualization of the argu-

ment used (Marrades& Gutierrez, 2000). From our

perspective the statistics indicates lack of synthetic

competence of 5 students of the Group 1 and 6 of

Group 2.

The StudetI’s case shows the existing of KSA

transferability from paper-and-pencil to DGS but the

lack of it in the reverse way. This means that the step

from empirical to deductive justiﬁcation is not easy

even for the students with relatively high math abili-

ties.

The roots of the inquiry based approach are in the

Socratic style. This style was applied in the ﬁrst group

after the individual work on Problem 2. The unlimited

time and the Socratic style provided some opportuni-

ties for creative work to the more able students, but

the tutoring instructional method applied in the sec-

ond group gave better statistics.

Our initial assumption that the Problem 1 is in the

zone of the actual development and Problem 2 after

the homework will be in the zone of the proximal

(and even actual) development of the students was too

optimistic, but our misunderestimation of these very

simple problems shows that the desired meaningful

inquiry-based approach in math education is nothing

more than a ﬁction for the regular classroom prac-

tice. In fact, during a regular lesson in traditional style

teachers consider at least 4-5 such simple problems

with rigor proofs.

On the contrary: the Socratic style is attractive

and effective way for new concepts to be introduced

and elaborated as extracurricular activity. During our

study we observed that Socratic style teaching geom-

etry enhanced with DGS environment does not lead to

van Hiele’s level 4 automatically, and in some cases

even reduces students’ critical thinking.

8 NOTES

Note 1. A frame of didactical technology for the

Thales Theorem was among the outcomes of the 3rd

meeting of MITE held in October 2006 in Orya-

hoviza, Bulgaria. During a workshop initiated by

the second author an international team designed this

frame with elements of ICT, compatible with curricu-

lum in Bulgaria, Russia and Kazakhstan.

Note 2. We borrow the word decontextualization

from (Marrades& Gutierrez, 2000) but we do not use

it in the same sense.

Note 3. We use the word metalanguage to denote

an expansion of the common math language used by

the students on the DGS icons, operators etc. The

general idea follows the description of the plurilin-

gualism given in the Common European Framework

of Reference for Languages (Language Policy Unit,

Strasbourg, www.coe.int/lang-CEFR): In different sit-

uations, a person can call ﬂexibly upon different parts

of this (communicative) competence to achieve effec-

tive communication with a particular interlocutor.

The Van Hiele’s level havespeciﬁc language (Van-

Hiele, 1984) which indicates the level. We observed

that the students working with DGS use also in spe-

ciﬁc manner the DGS interfacefor each level, i.e. they

’communicate’ with the computer in a manner that is

speciﬁc for the Van Hiele’s level reached. The com-

municative competence in this case is expressed via

metalanguage which is speciﬁc for the corresponding

Van Hiele’s level. A research to clarify the metalan-

guage is in progress in our team and an interim report

DetectingMath-and-ICTCompetence

157

was given at the ITA 2013 Winter Session, Dec 18-19,

2013, Soﬁa, Bulgaria.

REFERENCES

Baptist, P. et al. (eds.) (2011). SINUS international.

Bayreuth, University of Bayreuth.

European Commission (2004). Framework for key com-

petences in a knowledge-based society. http://ec.

europa.eu/education/policies/2010/doc/basicframe.pdf

(active in Nov 2013)

Rocard, M. et al. (2007). Science Education now. European

Commission, Directorate-General for Research, Sci-

ence, Economy and Society.

Lazarov, B. (2013) Socratic style teaching and synthetic

competence building of advanced students in mathe-

matics. DARYN, Astana, 18-19

Lazarov, B. and Sharkova, I. (2013). Two geometry illustra-

tions of the inﬁnitesimal method. Education and Tech-

nology. Vol 4/2013, 174-180. (in Bulgarian)

Marrades, R. and Gutierrez, A. (2000). Proofs produced by

secondary school students learning geometry in a dy-

namic computer environment. Educational Studies in

Mathematics, 44, 87-125.

Shabanova, M. et al. (2013) Learning mathematics with us-

ing opportunities of GeoGebra. Pero Pblsh, Moskva,

p 127. (in Russian).

Van Hiele, P. M. (1984). A child’s thought and geometry.

In D.Fuys, D.Geddes and R.Tischler (Eds), English

translation of selected writings of Dina van Hiele-

Geldof and P.M. van Hiele, 237-241. Brooklyn Col-

lege, N.Y. 1984.

Vygotsky, L. (1935). Dynamics of cognitive development

in relation to student learning. Mental development of

children in the learning process. Moscow-Leningrad,

33-52. (in Russian).

APPENDIX

We quote the deﬁnitions of the ﬁrst four Van Hiele’s

levels as given by Michael de Villiers in Some Re-

ﬂections on the Van Hiele theory (Invited plenary pre-

sented at the 4th Congress of teachers of mathemat-

ics of the Croatian Mathematical Society, Zagreb, 30

June - 2 July 2010).

Level 1 (Recognition). Pupils visually recognize

ﬁgures by their global appearance. They recognize

triangles, squares, parallelograms, and so forth by

their shape, but they do not explicitly identify the

properties of these ﬁgures.

Level 2 (Analysis). Pupils start analyzing the

properties of ﬁgures and learn the appropriate techni-

cal terminology for describing them, but they do not

interrelate ﬁgures or properties of ﬁgures.

Level 3 (Ordering). Pupils logically order the

properties of ﬁgures by short chains of deductions and

understandthe interrelationships between ﬁgures (e.g.

class inclusions).

Level 4 (Deduction). Pupils start developing

longer sequences of statements and begin to under-

stand the signiﬁcance of deduction, the role of ax-

ioms, theorems and proof.

We did not detected the ﬁfth level (Rigor) among

the students of our groups.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

158