
The Integer Approximation of Undirected Graphical Models
Nico Piatkowski, Sangkyun Lee and Katharina Morik
Artificial Intelligence Group, TU Dortmund University, 44227 Dortmund, Germany
Keywords:
Graphical Models, Approximate Inference.
Abstract:
Machine learning on resource constrained ubiquitous devices suffers from high energy consumption and slow
execution time. In this paper, it is investigated how to modify machine learning algorithms in order to reduce
the number of consumed clock cycles—not by reducing the asymptotic complexity, but by assuming a weaker
execution platform. In particular, an integer approximation to the class of undirected graphical models is
proposed. Algorithms for inference, maximum-a-posteriori prediction and parameter estimation are presented
and approximation error is discussed. In numerical evaluations on synthetic data, the response of the model
to several influential properties of the data is investigated. The results on the synthetic data are confirmed
with a natural language processing task on an open data set. In addition, the runtime on low-end hardware
is regarded. The overall speedup of the new algorithms is at least 2× while overall loss in accuracy is rather
small. This allows running probabilistic methods on very small devices, even if they do not contain a processor
that is capable of executing floating point arithmetic at all.
1 INTRODUCTION
Data analytics for streaming sensor data brings chal-
lenges for the resource efficiency of algorithms in
terms of execution time and the energy consumption
simultaneously. Fortunately, optimizations which re-
duce the number of CPU cycles also reduce energy
consumption. When reviewing the specifications of
processing units, one finds that integer arithmetic is
usually cheaper in terms of instruction latency, i.e. it
needs a small number of clock cycles until the result
of an arithmetic instruction is ready. This motivates
the reduction of CPU cycles in which code is executed
when designing a new, resource-aware learning algo-
rithm. Beside clock cycle reduction, limited memory
usage is also an important factor for small devices.
Outsourcing parts of data analysis from data cen-
ters to ubiquitous devices that actually measuredata
would reduce the communication costs and thus en-
ergy consumption. If, for instance, a mobile medical
device or smartphone can build a probabilistic model
of the usage behavior of its user, energy models can
be made more accurate and power management can
be more efficient. The biggest hurdle in doing this,
are the heavily restricted computational capabilities
of very small devices—some do not even have a float-
ing point processor. Consequently, computationally
simple machine learning approaches have to be con-
sidered. Low complexity of machine learning mod-
els is usually achieved by independence assumptions
among features or labels. In contrast, the joint predic-
tion of multiple dependent variables based on multi-
ple observed inputs is an ubiquitous subtask in real
world problems from various domains. Probabilistic
graphical models are well suited for such tasks, but
they suffer from the high complexity of probabilistic
inference.
In the paper at hand, it is shown that the frame-
work of undirected graphical models (Wainwright
and Jordan, 2007) can be mapped to an integer do-
main. Inference algorithms and a new optimization
scheme are proposed, that allow the learning of inte-
ger parameters without the need for any floating point
computation. This opens up the opportunity of run-
ning machine learning tasks on very small, resource-
constrained devices. To be more precise, based only
on integers, it is possible to compute approximations
to marginal probabilities, to maximum-a-posteriori
(MAP) assignments and maximum likelihood esti-
mate either via an approximate closed form solution
or an integer variant of the stochastic gradient de-
scent (SGD) algorithm. It turns out that the integer
approximations use less memory and deliver a rea-
sonable quality while being around twice as fast as
their floating point counterparts. To the best of our
knowledge, there is nothing like an integer undirected
model so far. The remainder of this paper is organized
as follows. This Section continues with an overview
296
Piatkowski N., Lee S. and Morik K..
The Integer Approximation of Undirected Graphical Models.
DOI: 10.5220/0004831202960304
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 296-304
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

on related work. A short introduction to probabilistic
graphical models is given in Section 2. In Section 3,
the intuition behind integer undirected graphical mod-
els is explained, and the corresponding algorithms are
derived. Furthermore, a bound on the training error is
presented. Two instances of the integer framework,
Integer Markov Random Fields and Integer Condi-
tional Random Fields, are evaluated in Section 4 on
synthetic and real world data. Finally, Section 5 con-
cludes this work.
1.1 Related Work
Many approximate approaches to probabilistic infer-
ence based on Belief Propagation (BP) (Kschischang
et al., 2001; Pearl, 1988) were proposed in the last
decade. Among them Counting BP (Kersting et al.,
2009), Lifted BP (Ahmadi et al., 2012), Stochastic BP
(Noorshams and Wainwright, 2011), Tree-reweighted
BP (Wainwright et al., 2003), Tree Block Coordinate
Descent (Sontag and Jaakkola, 2009) or Particle BP
(Ihler and McAllester, 2009). Unfortunately, most of
these methods are by no means suited for embedded
or resource constraint environments. In contrast to
these approaches, the model class that is proposed
in the paper at hand has the same asymptotic com-
plexity as the vanilla inference methods, but it uses
cheaper operations. Inspired by work from the signal
processing community (Hassibi and Boyd, 1998), the
underlying model class is restricted to the integers,
which results in a reduced runtime and energy sav-
ings, while keeping a good performance. This new
approach should not be confused with models that
are designed for integer state spaces, in which case
the state space X is a subset of the natural numbers
or, more generally, is a metric space. Here, the state
space may be an arbitrary discrete space without any
additional constraints.
Estimation in discrete parameter models was re-
cently investigated in (Choirat and Seri, 2012). They
discuss consistency, asymptotic distribution theory,
information inequalities and their relations with effi-
ciency and super-efficiency for a general class of m-
estimators. Unfortunately, the authors do not consider
the case when the true estimator is not included in the
search space and therefore, their analysis cannot be
used to estimate the error in a situation when the op-
timizer has to be approximated.
Bayesian network classifiers with reduced preci-
sion parameters have been introducedrecently(Tschi-
atschek et al., 2012). The authors evaluate empir-
ically the classification performance when reducing
the floating-point precision of probability parameters
of Bayesian networks. After learning the parameters
as usual in R (represented as 64 bit double precision
floating point numbers), they varied the bit-width of
mantissa and exponent, and reported the prediction
accuracy in terms of the normalized number of cor-
rectly classified test instances. They found that af-
ter learning, the parameters may be multiplied by a
sufficiently large integer constant (10
9
) to convert the
probabilities into integer numbers. Therefore, their
method still relies on floating point arithmetic for
learning and prediction. However, Tschiatschek et al.
missed the point that real valued probability parame-
ters are necessary for Bayesian networks but not for
all classes of probabilistic graphical models.
2 PROBABILISTIC GRAPHICAL
MODELS
The basic notation and concepts of probabilistic
graphical models in this Section are based on (Wain-
wright and Jordan, 2007), which is an excellent intro-
duction to this topic. Let G = (V,E) be an undirected
graph with |V| = n vertices, edge set E ⊂ V × V and
N
v
:= {w ∈ V : {v,w} ∈ E} the neighbors of vertex
v ∈ V. Each vertex v ∈ V corresponds to a random
variable X
v
with a realization x
v
and a domain X
v
with
at least two different states, i.e. |X
v
| ≥ 2. Consider
an n-dimensional random variable X = (X
v
)
v∈V
with
realization x ∈ X = ⊗
v∈V
X
v
. The probability of the
event {X = x} is denoted by p(X = x). p(x) is used
as a shortcut for p(X = x) in the remainder . For a
set of vertices A ⊆ V, X
A
is addressing the compo-
nents of X that correspond to the vertices in A. For
ease of notation, X
v
and X
{v}
are regarded the same.
For undirected graphical models, the joint probability
mass function of X is given by
p
θ
(x) =
1
Z(θ)
∏
C∈C (G)
ψ
C
(x
C
) (1)
Z(θ) =
∑
x∈X
∏
C∈C (G)
ψ
C
(x
C
) (2)
where C (G) is the set of all cliques
1
in G and Z(θ)
is the normalization constant (since it does not de-
pend on x). Let C be a clique of G and X
C
the cor-
responding joint domain of all vertices in C. The set
Ω is the domain of the parameters θ ∈ Ω
d
which is
usually the real line Ω = R. The parameter vector
contains |X
C
| weights for each clique C ∈ C (G), i.e.
θ = (θ
C
)
C∈C (G)
, which results in d =
∑
C∈C (G)
|X
C
|.
The compatibility functions ψ
C
(also known as fac-
1
A clique corresponds to a fully connected subgraph.
TheIntegerApproximationofUndirectedGraphicalModels
297

tors) are typically chosen to be
ψ
C
(x
C
) = exp(hθ
C
,φ
C
(x)i)
since this ensures positivity of p
θ
and leads to a
canonical form of the corresponding exponential fam-
ily member.
p
θ
(x) = exp(hθ,φ(x)i − A(θ))
The vector-valued function φ is a sufficient statistic
of X and may be understood as transformation of x
into a binary valued feature space φ : X → {0, 1}
d
and
A(θ) = logZ(θ). Sufficient statistics are called over-
complete, when there exists a vector a ∈ R
d
and a con-
stant b ∈ R, such that ha,φ(x)i = b, ∀x ∈ X . For con-
venience, the components of θ and φ are indexed by
C to denote the subvector of weights or features that
corresponds to a clique C. To address a certain com-
ponent of θ or φ, the corresponding event {X
C
= x
C
}
is used as an index, i.e. θ
X
C
=x
C
or even θ
C=x
C
.
If the parameters are known, the MAP prediction
for the joint state of all vertices can be computed by
x
∗
= argmax
x∈X
p
θ
(x) = argmax
x∈X
hθ,φ(x)i. (3)
A common choice for learning the parameters θ of an
undirected model is the maximum likelihood estima-
tion (MLE), where the likelihood (4) of the parame-
ters θ for given i.i.d. data
2
D is maximized.
L(θ | D) =
∏
x∈D
p
θ
(x) (4)
The MLE θ
∗
, i.e. the solution that maximizes L, has
a closed form, if and only if the underlying graphi-
cal structure is a tree or a triangulated graph. In this
case, θ
∗
is induced by the empirical expectation of the
sufficient statistic φ(x).
θ
∗
v=x
= logE
D
[φ
v=x
(x)], (5)
θ
∗
vu=xy
= log
E
D
[φ
vu=xy
(x)]
E
D
[φ
v=x
(x)]E
D
[φ
u=y
(x)]
(6)
The MLE θ
∗
for partially observed data and certain
classes of graphical models like Conditional Random
Fields (CRF) (Sutton and McCallum, 2012) can be
found with gradient based methods. Taking the loga-
rithm of (4), dividing by |D| and substituting (1) for
p
θ
(x) yields the average log-likelihood ℓ (7). Since
the logarithm is monotonic, maximizing ℓ will reveal
the optimizer of L. Since E
D
[φ(x)] =
1
|D|
∑
x∈D
φ(x),
ℓ is given by
ℓ(θ | D) = hθ,E
D
[φ(x)]i − lnZ(θ). (7)
2
It is assumed that every training instance in D is fully
observed.
Taking the natural logarithm to form the log-
likelihood is an arbitrary choice that may be replaced
with any other log
b
if desired. Since the second term
is the cumulant generating function of p
θ
, its par-
tial derivative is the expected sufficient statistic for a
given θ. This is plugged into the partial derivative of
ℓ w.r.t. θ
x
C
=x
C
(7) to obtain the expression (8).
∂ℓ(θ | D)
∂θ
x
C
=x
C
= E
D
[φ
x
C
=x
C
(x)] − E
θ
[φ
x
C
=x
C
(x)] (8)
Here, E
D
[φ
x
C
=x
C
(x)] denotes the empirical expecta-
tion of φ
x
C
=x
C
(x), i.e. its average value in D. By
using (8), the model parameters θ can be estimated
by any first-order optimization technique. In the fol-
lowing, it is explained shortly how E
θ
[φ
x
C
=x
C
(x)] is
computed with BP. From now on, assume that the un-
derlying graphical structure is a tree. The maximum
clique size is thus 2. The message update rule is
m
v→u
(x
u
) =
∑
x
v
∈X
v
ψ
vu
(x
v
,x
u
)ψ
v
(x
v
)
∏
w∈N
v
\{u}
m
w→v
(x
v
).
(9)
The messages m
v→u
(x
u
) are computed for all pairs of
vertex v ∈ V and neighbor u ∈ N
v
until convergence.
Converged messages are denoted by m
∗
v→u
(x
u
). The
product of all incoming messages of a vertex is given
by M
v
(x) :=
∏
u∈N
v
m
u→v
(x). After convergence, the
vertex marginal probabilities p
v
(x
v
) that are implied
by θ can be computed with
p
v
(x
v
) =
ψ
v
(x
v
)M
∗
v
(x
v
)
∑
x∈X
v
ψ
v
(x
v
)M
∗
v
(x)
(10)
whereas M
∗
v
(x) is the product of converged mes-
sages m
∗
v→u
(x
u
). The interested reader is referred to
(Kschischang et al., 2001) for a discussion on BP and
related algorithms.
3 THE INTEGER
APPROXIMATION
In their book on graphical models, Wainwright and
Jordan (Wainwright and Jordan, 2007) stated that ”It
is important to understand that for a general undi-
rected graph the compatibility functions ψ
C
need not
have any obvious or direct relation to marginal or con-
ditional distributions defined over the graph cliques.
This property should be contrasted with the directed
factorization, where the factors correspond to condi-
tional probabilities over the child-parent sets.” This
explains why it could be possible to have an undi-
rected graphical model that is parametrized by inte-
gers. However, there is some work to do. For ex-
cluding every floating point computation, the identi-
fication of integer parameters is not enough. That is,
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
298

the computations for training and prediction have to
be based on integer arithmetic. Lastly, integer ap-
proximation should still deliver a reasonable quality
in terms of training error and test error.
The first step towards integer models is directly
related to the above statement. Strictly speaking, the
parameter domain Ω is restricted to the set of inte-
gers N and a new potential function is defined as
ψ
C
(x
C
) := 2
hθ
C
,φ
C
(x)i
= exp(ln(2)hθ
C
,φ
C
(x)i). (11)
Considering parameters θ ∈ R
d
of a model that has
potential function ψ
C
(x
C
), it is easy to see that replac-
ing ψ
C
(x
C
) with ψ
C
(x
C
) does not alter the marginal
probabilities as long as the parameters are scaled
by
1
/ln2. By this, it is possible to convert integer pa-
rameters that are estimated with
ψ
C
(x
C
) to ψ
C
(x
C
)
(and vice versa), without altering the resulting proba-
bilities. Notice that
ψ
C
(x
C
) can be computed by log-
ical bit shift operations which consume which does
consume less clock cycles than the corresponding
transcendental functions required to compute ψ
C
(x
C
).
As already mentioned above, it requires θ ∈ N
d
for
ψ
C
(x
C
) to be integer and hence the product of com-
patibility functions in Eq. (1) and the normalization
constant Eq. (2) are computable by means of non-
negative integer arithmetic. By this, the probabili-
ties that are computed by the model are rational, i.e.
p(x) ∈ [0, 1] ∩ Q and may be represented as a pair of
natural numbers. Nevertheless, actual probability val-
ues are not required at all for estimating the integer
model parameters and to compute MAP predictions.
3.1 Inference
Recalling the message update Eq. (9), one sees that
all messages are integer valued, if Ω ⊆ N, ψ
C
(x
C
) is
replaced by
ψ
C
(x
C
) and the initial messages are set to
1. Thus, the whole message computation and propa-
gation procedure is already stated without any floating
point computation. Nevertheless, recall that the inte-
ger width of a CPU is constrained by its wordsize ω.
m
v→u
(x) may exceed the machine integer precision
limit 2
ω
quite easily. Thus, many overflows could
occur during message computations which destroy
the semantics of the messages and the results are no
longer meaningful. First attempts to make the compu-
tation more robust against overflows relied on the fact
that messages m
v→u
(x) may be scaled arbitrarily with-
out changing the resulting marginal probabilities as
long as the same scale is used for all x. Nevertheless,
the messages cannot be simply divided by their sum
as is the case with floating point arithmetic, since inte-
ger division will pin all messages down to 0. Numer-
ous attempts to scale the integer messages by bit shift
p
θ
(X
C
= x
C
)
0
0.25
0.5
0.75
1
0 0.25 0.5 0.75 1
ˆp
θ
(X
C
= x
C
)
Figure 1: Estimates of edge marginal probabilities for
50 random trees with 50 nodes and 2 states per node.
Marginals are computed by the bit length approximation ( ˆp)
and vanilla BP (p) on the same parameter vector θ.
operations only worked on relatively small graphical
structures, but all those approaches suffered from the
loss of information that occurred whenever too many
bits had to be shifted out in order to prevent overflows.
As a solution to this problem, new messages are
defined. Instead of computing the original sum-
product messages, we proposeto compute an approxi-
mation to the integer message bit length. The approxi-
mate bit length β
vu
(y) and the corresponding message
ˆm
vu
(y) := 2
β
vu
(y)
are given by
β
vu
(y) := max
x
θ
vu=xy
+θ
v=x
+
∑
w∈N
v
\{u}
β
wv
(x). (12)
How m and ˆm are related to each other is a natu-
ral question. The messages ˆm that result from the
bit length approximation resemble max-product mes-
sages (Kschischang et al., 2001). Their magnitude is
related to the original messages m through the follow-
ing lemma.
Lemma 1. Let (v,u) ∈ E be an edge of tree G =
(V, E), h
v
:= |X
v
| the size of vs state space and n
v
:=
N
v
the number of its neighbors. If ∀y ∈ X
u
: ∃x ∈ X
v
:
θ
vu=xy
+ θ
v=x
> 0, then ˆm
vu
(x) < m
vu
(x) ≤ ˆm
vu
(x)
h
v
.
This statement can be proven by induction over
the degree n
v
of v. The fact that the exclusion of all-0
vertex and edge parameters is a rather safe assump-
tion, will be revealed later, when the integer parame-
ter estimation is described.
When it comes to the point-wise estimates of the
marginal probabilities, one finds that due to the ap-
proximate messages some marginal probabilities sim-
ply cannot be present. In Figure 1, edge marginal
probabilities Eq. (10) are plotted that are computed
with m and ˆm, respectively, while using the same pa-
rameters for both models. One clearly sees how the
probability space is discretized by the approximate
messages. One can also see that there is an error in the
TheIntegerApproximationofUndirectedGraphicalModels
299

approximate marginal probabilities computed with ˆm.
In case of zero error all points would lie on the diag-
onal.
The previous lemma helps to derive an estimate
of the distance between the true outcome of the infer-
ence and the one that results from the message update
Eq. (12).
Theorem 1. Let β
∗
v
:= max
y
max
u
β
uv
(y) be the max-
imum incoming bit length at v and assume that the
preconditions of Lemma 1 hold, then
D(p
v
k ˆp
v
) ∈ o
n
v
h
2
v
β
∗
v
.
where D(p
v
k ˆp
v
) denotes the Kullback-Leibler (KL)
divergence between the marginal probability mass
function p
v
, computed with the message update
m
vu
(y), and ˆp
v
, computed with ˆm
vu
(y).
This result can be derived by plugging the BP
marginals (10) into the definition of the KL diver-
gence and applying Lemma 1 two times. The KL is
still unbounded, since there is no bound on β
∗
v
. Never-
theless, it indicates a dependence of the KL of p
v
and
ˆp
v
on the state space size |X
v
| and the neighborhood
size |N
v
|. This relation can also be observed in the nu-
merical experiments in Section 4. A comprehensive
discussion of how message errors affect the result of
belief propagation can be found in (Ihler et al., 2005).
3.2 Parameter Estimation
In the following, an integer parameter estimation
method based on the closed form solution to the MLE
is derived. Recall that E
D
[φ(x)] =
1
|D|
∑
x∈D
φ(x)
and let f :=
∑
x∈D
φ(x) and bla := ⌊log
2
a⌋ + 1 the
bit length of a. By approximating the logarithm in
Eqs. (5) and (6) with bl, an integer approximation to
the optimal parameters can be found:
˜
θ
v=x
:= bl f
v=x
− bl|D| ≈ log
2
E
D
[φ
v=x
(x)]
˜
θ
vu=xy
:= bl f
vu=xy
− bl f
v=x
− bl f
u=y
+ bl|D|
≈ log
2
E
D
[φ
vu=xy
(x)]
Unfortunately, most of those estimates are negative
which is not allowed due to the integer restriction. In
case of negative parameters, let λ := | max
1≤i≤d
−
˜
θ
i
|
be the absolute value of the smallest component of
˜
θ.
Now, consider the weights
˜
θ
+
v=x
:= s+
˜
θ
v=x
,
˜
θ
+
vu=xy
:= s+
˜
θ
vu=xy
with s := (λ,λ,...,λ)
⊤
∈ R
d
. The new parameters
˜
θ
+
are non-negative, but an error is induced into
˜
θ by
replacing log
2
with bl. The following lemma shows
that shifting
˜
θ by s introduces no new error.
Lemma 2. Let s := (c,c,.. . ,c)
⊤
∈ R
d
with arbitrary
c and let φ be an overcomplete sufficient statistic, then
ℓ(θ+ s) = ℓ(θ).
The statement follows from the definitions of log-
likelihood and overcompleteness. This shows that it
is safe to assume ∀y ∈ X
u
: ∃x ∈ X
v
: θ
vu=xy
+ θ
v=x
>
0 for Lemma 1, since we can enforce all parameters
to be positive without touching the likelihood. It is
also possible to bound the training error of the shifted
integer parameters
˜
θ
+
:
Theorem 2. Let θ
∗
be as defined by Eqs. (5) and
(6) and
˜
θ
+
as defined above, then ℓ(θ
∗
) − ℓ(
˜
θ
+
) ≤
k∇f(
˜
θ
+
)k
1
.
The result follows from the previous lemma and
the definition of convexity.
Either due to restrictions in wordsize ω or for en-
larging the number of representable marginal prob-
abilities, a final scaling of the parameters might
be desired. To allow an appropriate integer scal-
ing, a parameter K := |Ω| is introduced: Let γ :=
max
1≤i≤d
−
˜
θ
i
be the negative component of
˜
θ with
the largest magnitude and κ := max
1≤i≤d
˜
θ
i
be the
component of
˜
θ with the largest magnitude. The fi-
nal integer parameters are computed by
¯
θ
v=x
:=
K
κ− γ
˜
θ
+
v=x
,
¯
θ
vu=xy
:=
K
κ− γ
˜
θ
+
vu=xy
.
(13)
Thus,
˜
θ
+
is rescaled such that
¯
θ ∈ {0, 1, . ..,K}
d
,
which may also be interpreted as implicit base
change. Note that unless K = (κ − γ), the parameter
vector is scaled and an additional approximation error
is added. Hence, the impact of K is empirically evalu-
ated in Section 4. The method of choosing parameters
according to (13) is called direct integer estimation.
3.3 Gradient based Estimation
As mentioned in Section 2, in certain situations, it
might be desired to estimate the parameters with
gradient based methods. Unfortunately, the partial
derivatives from Eq. (8) are not integral. The expres-
sion must be rearranged to obtain an integer form. Let
f :=
∑
x∈D
φ(x) and
ˆ
M
∗
v
:=
∑
y∈X
v
ˆ
M
∗
v
(y), it is
ˆ
M
∗
v
|D|
∂ℓ(θ | D)
∂θ
X
v
=x
v
=
ˆ
M
∗
v
f
v=x
v
− |D|
ˆ
M
∗
v
(x
v
).
This scaled version of the partial derivative is an in-
teger expression that can be computed by using only
integer addition, multiplication and binary bit shift.
The common gradient descent update makes use of
a stepsize η to determine how far the current weight
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
300

vector should move into the direction of the gradi-
ent. The smallest possible step size in integer space
is 1. This means that any parameter can either be in-
creased or decreased by 1. In the beginning of an inte-
ger gradient based optimization, the gradient will tell
to increase a quite large number of parameters. This
results in rather slow convergence, since due to the
fixed step size of 1, most of the parameters are worse
than before the update. To compensate for this, we
suggest to update, for each clique, only the parameter
for which the corresponding partial derivative has the
largest magnitude. This method is used when estimat-
ing the CRF parameters in the following section.
4 NUMERICAL RESULTS
The previous sections pointed out various factors that
may have an influence on training error, test perfor-
mance or runtime of the integer approximation. In
order to show that integer undirected models are a
quite general approach for approximate learning in
discrete state spaces, generative and discriminative
variants of undirected models are evaluated on syn-
thetic data and real world data. In particular the fol-
lowing methods are considered: RealMRF: The clas-
sic generative undirected model as described in Sec-
tion 2. RealCRF: The discriminative classifier as it
is defined in (Lafferty et al., 2001; Sutton and Mc-
Callum, 2012). IntMRF: The integer approximation
of generative undirected models as described in Sec-
tion 3. IntCRF: The integer approximation of dis-
criminative undirected models. Further details are ex-
plained in Section 4.4. Both real variants are based
on floating point arithmetic. In the MRF experiments,
the model parameters are estimated from the empiri-
cal expectations by Eqs. (5), (6) and (13). Parameters
of discriminative models are estimated by stochas-
tic gradient methods (Sutton and McCallum, 2012).
Each MRF experiment was repeated 100 times on ran-
dom input distributions and graphs. In most cases,
only the average is reported, since the standard devi-
ation was too small to be visualized in a plot. When-
ever MAP accuracy is reported, it corresponds to the
percentage of correctly labeled vertices, where the
prediction is computed with Eq. (3).
The implementations
3
of all evaluated methods
are equally efficient, e.g. the message computation
(and therefore the probability computation) executes
exactly the same code, except for the arithmetic in-
structions. Unless otherwise explicitly stated, the ex-
periments are done on an Intel Core i7-2600K 3.4GHz
3
For reproducibility, all data and code is available at
http://sfb876.tu-dortmund.de/intmodels.
(Sandy Bridge architecture) with 16GB 1333MHz
DDR3 main memory.
Synthetic Data. In order to achieve robust results
that capture the average behavior of the integer ap-
proximation, a synthetic data generator has been im-
plemented that samples random empirical marginals
with corresponding MAP states. Therefore, a sequen-
tial algorithm for random trees with given degrees
(Blitzstein and Diaconis, 2011) generates random tree
structured graphs. For a random graph, the weights
θ
∗
i
∼ N (0,1) are sampled from a Gaussian distribu-
tion. Additionally, for each vertex, a random state is
selected that gets a constant extra amount of weight,
thus enforcing low entropy. The weights are then used
to generate marginals and MAP states with the double
precision floating point variant of belief propagation.
The generated marginals serve as empirical input dis-
tribution and the MAP state is compared to the MAP
state that is estimated by IntMRF and RealMRF.
CoNLL-2000 Data. This data set was proposed for
the shared task at the Conference on Computational
Natural Language Learning in 2000 and is based on
the Wall Street Journal corpus. The latter contains
word-features and one label, called chunk tag, per
word. In total, there are 22 chunk tags that correspond
to the vertex states, i.e. |X | = 22. For the computa-
tion of per chunk F
1
-score, a chunk is only treated as
correct, if and only if all consecutive tags that belong
to the same chunk are correct. The data set contains
8936 training instances and 2012 test instances. Be-
cause of the inherent dependency between neighbor-
ing vertex states, this data set is well suited to evaluate
whether the dependency structure between vertices is
preserved by the integer approximation.
4.1 The Impact of |X | and |N
v
| on
Quality and Runtime
In Section 3 an estimate of the error in marginal prob-
abilities that are computed with bit length BP (Sec-
tion 3.1) indicates that the size of the vertex state
space |X
v
| and the degree |N
v
| have an impact on the
training error. In Figure 2, the training error in terms
of normalized negative log-likelihood, the test error
in terms of MAP accuracy and the runtime in seconds
for two values of |X
v
| and |N
v
| for an increasing num-
ber of vertices on the synthetic data are shown. Each
point in each curve is the average over 100 random
trees with random parameters. The results with vary-
ing |X
v
| are generated with a maximum degree of 8
and the ones for varying |N
v
| with |X
v
| = 4.
In terms of training error, the mid-right plot shows
a clear offset between integer and floating point es-
timates for the same number of states. In terms of
TheIntegerApproximationofUndirectedGraphicalModels
301

MAP Accuracy
0.85
0.9
0.95
1
10 100 1000
Int, deg=4
Int, deg=16
Real, deg=4
Real, deg=16
0.4
0.6
0.8
1
10 100 1000
Int, |X|=4
Int, |X|=16
Real, |X|=4
Real, |X|=16
−ℓ(θ)/(|V| + |E|)
0.4
0.5
0.6
0.7
10 100 1000
0
0.75
1.5
2.25
10 100 1000
Seconds
0
0.07
0.14
0.21
0 2500 5000 7500
0
0.75
1.5
2.25
0 2500 5000 7500
|V| |V|
Figure 2: MRF test accuracy (top), training error (center)
and runtime in seconds (bottom) for different choices of
maximum vertex degree (left column) and state space size
(right column) as a function of the number of vertices (x-
axis). The plots in each column share the same key that is
defined in the top row. The plots in the first two rows have
their x-axis in logarithmic scale. IntMRF results are gener-
ated with K = 8.
varying degrees (mid-left), the training error of the in-
teger model responds to different neighborhood sizes
whereas the likelihood of the floating point model is
invariant against the degrees. A similar picture is
drawn for the dependence of the test accuracy with
|X | in the top-left and |N
v
| in the top-right plot, re-
spectively. The floating point MAP estimate is al-
ways correct and not changed by an increasing num-
ber of states and neighbors, whereas the performance
of IntMRF drops with an increasing number of ver-
tices but actually increases with increasing degrees.
The curves that correspond to RealMRF are not
visible in the top row of Figure 2, since this model
gets 100% accuracy on the synthetic data in nearly
all runs and therefore, its curve lies close to the hor-
izontal 1-line. However, in the two plots at the bot-
tom of Figure 2, one can see that the resource con-
sumption in terms of clock cycles is largely reduced
by the integer model. The time therein is measured
for estimating parameters, computing the likelihood,
and performing a MAP prediction. Since both al-
gorithms (RealMRF and IntMRF) share exactly the
same asymptotic complexity for these procedures, the
substantial reduction in runtime that is shown in the
results must be due to the reduction in clock cycles.
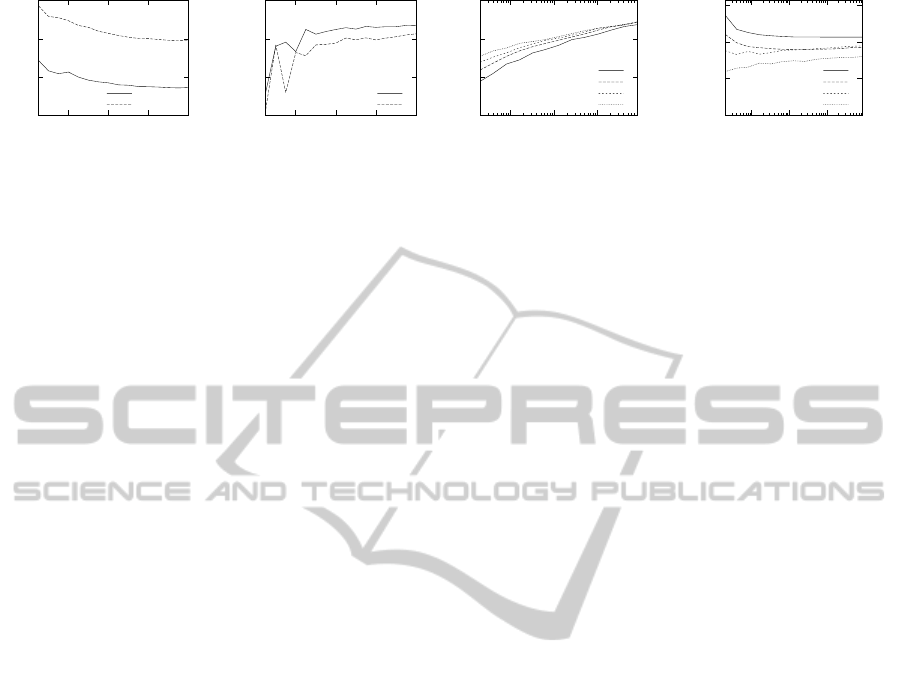
4.2 The Contribution of K to Quality,
Gradient and Memory
Consumption
As described in Section 3.2, the integer parameter
vector
¯
θ is scaled to be in the set Ω
d
K
:= {0, 1, . ..,K}
d
.
The effect of such scaling is illustrated by the re-
sponse of the integer model to the magnitude of K
in terms of training quality and test error, shown in
the two plots on the top of Figure 3. The training er-
ror seems to be a quite smooth function of K whereas
the MAP accuracy is sensitive to choices of K. This
could be expected, since a large K means that a larger
number of marginal probabilities can be represented.
One can also see that, as soon as K is large enough,
(i.e. K = 8 in the first two plots in Figure 3) a further
increase in K does not show any significant impact on
either training error and test accuracy. Both results
are generated on graphs with a maximum degree of 8,
but as already known from the previous experiment,
the effect of different degrees on the model quality is
negligible. In the third plot of Figure 3, the width of
the intrinsic parameter space is shown, i.e. the differ-
ence of the largest and the smallest parameter before
rescaling. The difference (κ− γ) seems to convergeto
the same value for various configurations of n and X .
Plotting κ and γ separately shows that the dynamics
in (κ − γ) are mainly influenced by the smallest pa-
rameter γ, i.e., the width of the parameter space must
increase in order to represent small probabilities.
As indicated by the analysis of the training error
in Section 3, the distance between the maximum like-
lihood estimate and the result of the direct integer pa-
rameter estimation is bounded by the gradient norm
of the integer parameters
¯
θ. Since the components
of the gradient are differences of probabilities, their
value cannot exceed 1 and a trivial upper bound for
the ℓ
1
-norm of the gradient is therefore d. An impor-
tant observation can be made in the rightmost picture
of Figure 3 which shows the relative gradient norm
for an increasing number of vertices and various val-
ues K. This result suggests that there exists a bound
on the relative gradient norm that is independent of
the number of vertices and that this bound decreases
with increasing K.
Furthermore, K has a strong impact on the over-
all memory consumption of the model. Let ω be the
floating point wordsize of the underlying architecture.
The Real model will require d × ω bit, whereas the
Int model has a size of d × blK (cf. Section 3.2) bit.
Thus, the Int model will use less memory whenever
blK < ω. In practice, a specialized data structure is
required to observe the reduced memory consump-
tion. In the second plot of Fig. 3 and the last two plots
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
302
−ℓ(θ)/(|V| + |E|)
0
0.7
1.4
2.1
4 8 12 16
Int, |X|=4
Int, |X|=16
MAP Accuracy
0
0.4
0.8
1.2
4 8 12 16
Int, |X|=4
Int, |X|=16
κ− γ
0
7
14
21
10 100 1000
Int, |X|=2
Int, |X|=4
Int, |X|=8
Int, |X|=16
k∇ℓ(θ)k
1
/d
0
0.016
0.032
0.048
10 100 1000
Int, K=1
Int, K=2
Int, K=4
Int, K=6
K K |V| |V|
Figure 3: From left to right: (I) negative log-likelihood of IntMRF as a function of K, i.e. the size of the parameter domain.
(II) MAP accuracy of MRF as a function of K. (III) Natural size of the parameter domain as a function of the number of
vertices (in log-scale) for different state space sizes, whereas γ is the smallest and κ the largest element of the corresponding
estimated parameter vector. (IV) The relative ℓ
1
-norm of the gradient for various values of K as a function of the number of
vertices (in log-scale).
of Fig. 4, one can see that K ∈ {6, 8} seems to be a
reasonable choice for these data sets, which reduces
the memory consumption of the model by a factor of
20, compared to a 64 bit floating point model.
4.3 Integer Models on Resource
Constrained Devices
The motivation for the integer model was to save re-
sources in terms of clock cycles. Here, it is demon-
strated that the impact of this reduction is larger, if
the underlying architecture is weaker, i.e. has slower
floating point arithmetic. A runtime comparison of
the integer MRF on two different CPU architectures
is shown in Figure 4. One is the Sandy Bridge, which
has also been the platform for all the other experi-
ments, and the second one is a Raspberry Pi device
with the ARM11 architecture. As expected, the in-
teger model actually speeds up the execution on the
Pi device more than on the other architecture, i.e. the
Raspberry Pi gains a speedup of 2.56× and the Sandy
Bridge a speedup of 2.34×. In terms of standard de-
viation, the ARM11 architecture is more stable than
the Sandy Bridge, which might be a result of a more
sophisticated out-of-order execution in the latter ar-
chitecture.
4.4 Training Integer CRF with
Stochastic Integer Gradient Descent
In the last evaluation, discriminative models for chain
structured data are investigated. A linear-chain CRF
is constructed on the CoNLL-2000 data and trained
by a SGD algorithm. The floating point CRF is
trained with stepsize η = 10
−1
. Integer parameter
updates are computed by means of the scaled integer
gradient (cf. the end of Section 3). Both algorithms
perform 20 passes over the training data, each pass
looping through the training instances in random or-
der, whereby IntCRF was trained with three different
parameter domain sizes K ∈ {2,4,6}. This was re-
peated 50 times in order to compute an estimate of
the expected quality of the randomized training pro-
cedure. Training error and test error are reported in
Figure 4 as a function of runtime in seconds. The neg-
ative log-likelihood is averaged over all training in-
stances and the accuracy is computed w.r.t. the chunk
type. One clearly sees that K = 2 results in poor train-
ing and test performances. Nevertheless, IntCRF with
K ∈ {4,6} reaches nearly the same performanceas the
double precision model, while using less computa-
tional resources per SGD iteration. Furthermore, the
average precision, recall and F
1
-score were computed
for each chunk type. As desired, the performance of
the integer approximation is reasonable. Except for
one chunk type (VP), the difference in F
1
-score be-
tween both methods is below 5%. Surprisingly, the
IntCRF has a higher precision than the RealCRF for
three chunk types. Averaged over all 22 chunk types,
the IntCRF has < 1% less precision, recall and F
1
-
score than RealCRF.
5 CONCLUSIONS AND FUTURE
WORK
In this work, integer undirected graphical models
have been introduced together with algorithms for
probabilistic inference and parameter estimation that
rely only on integer arithmetic. Generative and dis-
criminative models have been evaluated in terms of
prediction quality and runtime. On different archi-
tectures, an average speedup of at least 2× can be
achieved while accepting a reasonable loss in accu-
racy. One of the findings from the empirical evalu-
ation was the fact, that the model parameters have a
rather small magnitude. Thus, only a few bits are re-
quired for each parameter, which reduces the models
size by more than 20× compared to the eight bytes
that are required to store 64 bit double precision pa-
rameters. Overall, the results show that our method is
TheIntegerApproximationofUndirectedGraphicalModels
303

Seconds
0
0.4
0.8
1.2
2 4 8 16
Int
Real
Seconds
0
0.015
0.03
0.045
2 4 8 16
Int
Real
−ℓ(θ)
0
0.75
1.5
2.25
0 125 250 375
Int, K=2
Int, K=4
Int, K=6
Real
MAP Accuracy
0.923
0.936
0.949
0.962
0 125 250 375
Int, K=2
Int, K=4
Int, K=6
Real
|X
v
| |X
v
| Seconds Seconds
Figure 4: From left to right: Runtime comparison of integer and floating point MRF on two architectures for a varying number
of states. (I) Raspberry PI @ 700MHz (ARM11). (II) Intel Core i7-2600K @ 3.4GHz (Sandy Bridge). Progress of stochastic
gradient training in terms of (III) training error and (IV) test accuracy as a function of runtime.
especially well suited for small, mobile devices. Be-
side the introduction of integer models, average run-
times of probabilistic models have been investigated
and optimized in the context of resource constraint de-
vices. The experimental results indicate that a tight
bound on the training error might exist. Therefore,
future work will focus on tighter error bounds.
ACKNOWLEDGEMENTS
This work has been supported by Deutsche
Forschungsgemeinschaft (DFG) within the Col-
laborative Research Center SFB 876 “Providing
Information by Resource-Constrained Data Analy-
sis”, projects A1 and C1.
REFERENCES
Ahmadi, B., Kersting, K., and Natarajan, S. (2012). Lifted
online training of relational models with stochastic
gradient methods. In Machine Learning and Knowl-
edge Discovery in Databases, volume 7523 of Lecture
Notes in Computer Science, pages 585–600.
Blitzstein, J. and Diaconis, P. (2011). A sequential im-
portance sampling algorithm for generating random
graphs with prescribed degrees. Internet Mathmatics,
6(4):489–522.
Choirat, C. and Seri, R. (2012). Estimation in discrete pa-
rameter models. Statistical Science, 27(2):278–293.
Hassibi, A. and Boyd, S. (1998). Integer parameter estima-
tion in linear models with applications to gps. IEEE
Transactions on Signal Processing, 46(11):2938–
2952.
Ihler, A. and McAllester, D. (2009). Particle belief propaga-
tion. In Proceedings of the Twelfth International Con-
ference on Artificial Intelligence and Statistics, pages
256–263, JMLR: W&CP 5.
Ihler, A. T., III, J. W. F., and Willsky, A. S. (2005). Loopy
belief propagation: Convergence and effects of mes-
sage errors. Journal of Machine Learning Research,
6:905–936.
Kersting, K., Ahmadi, B., and Natarajan, S. (2009). Count-
ing belief propagation. In Proceedings of the Twenty-
Fifth Conference on Uncertainty in Artificial Intelli-
gence, pages 277–284,
Kschischang, F. R., Frey, B. J., and Loeliger, H.-A. (2001).
Factor graphs and the sum-product algorithm. IEEE
Transactions on Information Theory, 47(2):498–519.
Lafferty, J. D., McCallum, A., and Pereira, F. C. N. (2001).
Conditional random fields: Probabilistic models for
segmenting and labeling sequence data. In Proceed-
ings of the Eighteenth International Conference on
Machine Learning, pages 282–289
Noorshams, N. and Wainwright, M. (2011). Stochas-
tic belief propagation: Low-complexity message-
passing with guarantees. In Communication, Control,
and Computing 49th Annual Allerton Conference on,
pages 269–276.
Pearl, J. (1988). Probabilistic reasoning in intelligent sys-
tems: networks of plausible inference. Morgan Kauf-
mann Publishers Inc., San Francisco, CA, USA.
Sontag, D. and Jaakkola, T. (2009). Tree block coordinate
descent for MAP in graphical models. In Proceedings
of the Twelfth International Conference on Artificial
Intelligence and Statistics , volume 8, pages 544–551.
JMLR: W&CP.
Sutton, C. and McCallum, A. (2012). An introduction to
conditional random fields. Foundations and Trends in
Machine Learning, 4(4):267–373.
Tschiatschek, S., Reinprecht, P., M¨ucke, M., and Pernkopf,
F. (2012). Bayesian network classifiers with reduced
precision parameters. In European Conference on Ma-
chine Learning and Principles and Practice of Knowl-
edge Discovery in Databases.
Wainwright, M. J., Jaakkola, T. S., and Willsky, A. S.
(2003). Tree-reweighted belief propagation algo-
rithms and approximate ML estimation by pseudo-
moment matching. In 9th Workshop on Artificial In-
telligence and Statistics.
Wainwright, M. J. and Jordan, M. I. (2007). Graphical Mod-
els, Exponential Families, and Variational Inference.
Foundations and Trends in Machine Learning, 1(1–
2):1–305.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
304
