Formatting Bits to Better Implement Signal Processing Algorithms

Benoit Lopez

, Thibault Hilaire

and Laurent-St

ephane Didier

LIP6, Pierre and Marie Curie University (UPMC Univ Paris 06), Paris, France

IMATH, University of the South, Toulon-Var (USTV), Toulon, France

Keywords:

Fixed-point Arithmetic, Accurate Sum-of-Products, Bit Formatting, Digital Signal Processing Implementa-

tion.

Abstract:

This article deals with the ﬁxed-point computation of the sum-of-products, necessary for the implementation

of several algorithms, including linear ﬁlters. Fixed-point arithmetic implies output errors to be controlled.

So, a new method is proposed to perform accurate computation of the ﬁlter and minimize the word-lengths of

the operations. This is done by removing bits from operands that don’t impact the ﬁnal result under a given

limit. Then, the ﬁnal output of linear ﬁlter is guaranteed to be a faithful rounding of the real output.

1 INTRODUCTION

Usually, embedded digital signal processing algo-

rithms are speciﬁed using ﬂoating-point arithmetic

and next implemented using ﬁxed-point (FxP) arith-

metic (Padgett and Anderson, 2009) for cost, size and

power consumption reasons. FxP arithmetic is used

as an approximation of real numbers based on inte-

gers and implicit ﬁxed scaling by a power of 2. Of

course, the quantization of coefﬁcients and the round-

ing errors due to FxP computations lead to a degraded

numerical accuracy of the implemented algorithm.

Therefore, it is a great interest for the designer of em-

bedded system to determine and control the imple-

mentation error while maintaining low computational

effort.

In ﬁxed-point arithmetic, a main current prob-

lem is to minimize the word-lengths of operands

under constraints of precision in order to minimize

area and/or power consumption (Constantinides et al.,

2004). In this paper, a new method to reduce the

number of bits to consider in each sum-of-products

(SoP, also called Multiply-And-Accumulate) is pro-

posed. The SoPs are one of the elementary operations

of DSP algorithms. The main point of our approach

is that if the ﬁnal ﬁxed-point format is known, then

the bits having no impact in the ﬁnal result can be

detected and therefore discarded. Each term of the

sum-of-products can be then reformatted into a new

ﬁxed-point format having less bits.

Some ﬁxed-point arithmetic deﬁnitions and nota-

tions are reminded in section ??. Section 3 formalizes

the proposed approach, which is decomposed into two

formatting, for most signiﬁcant bits and least signif-

icant bits, respectively. Section 4 describes the error

analysis for Direct Form I ﬁlters implemented with

the bit formatting technique. Finally, an illustrative

example is given with a 4

order Butterworth ﬁlter,

before conclusion in section 6.

2 FIXED-POINT ARITHMETIC

AND SUM-OF-PRODUCTS

In this article we consider signed FxP arithmetic in

two’s complement representation. Let x be such a FxP

number with w bits as word-length:

x = −2

m−1

∑

i=`

(1)

where x

∈ B , {0,1} is the i

bit of x, m and ` are the

position of the most signiﬁcant bit (MSB) and least

signiﬁcant bits (LSB), respectively (Fig. 1). It can be

noted that m > ` and

w = m − ` +1. (2)

In a digital system, x is represented by an integer X ,

composed by the w bits {x

}

`6i6m

. In other words,

X = x.2

−`

, or equivalently

X = −2

m−`

m−`−1

∑

i=0

i+`

. (3)

104

Lopez B., Hilaire T. and Didier L..

Formatting Bits to Better Implement Signal Processing Algorithms.

DOI: 10.5220/0004711201040111

In Proceedings of the 4th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2014), pages

104-111

ISBN: 978-989-758-000-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

m + 1

−`

−2

−1

m−1

Figure 1: Fixed-point representation. m and ` are the posi-

tion of the MSB and LSB respectively (in this ﬁgure, m = 5

and ` = −4).

Through this paper the notation (m,`) is used to

denote the Fixed-Point Format (FPF) of such a ﬁxed-

point number and m, ` and w will be sufﬁxed by the

variable or constant they refer to.

Remark 1. In FxP arithmetic, there is no restriction

on the the position of the MSB and LSB. The FPF is

often chosen with m > 0 and ` 6 0. FPF with ` > 0

are also possible (the quantization step is greater than

1) or m < 0 (the largest represented number is lower

than

2.1 Conversion from Real to

Fixed-point

Many SoP-based DSP algorithms involve real coefﬁ-

cients that have to be converted into FxP arithmetic.

Let consider a real constant c ∈ R

∗

. The position of

the most signiﬁcant bit m of its w-bit wide FxP repre-

sentation in binary two’s complement is:

m =





log

|c|



if c < 0



log

|c|



+ 1 if c > 0

(4)

where b·cand d·e are the round to the integer towards

minus inﬁnity and round towards plus inﬁnity opera-

tors, respectively.

For some very special cases, eq. (4) should be

adapted (Hilaire and Lopez, 2013). The position of

the least signiﬁcant bit ` is deduced from eq. (2) and

the w-bit integer C representing c is computed:

C =

c.2

(5)

where b·e is the round to the nearest integer operator.

2.2 Sum-of-Products

In digital signal processing, the computation of ﬁl-

ter or controller algorithms requires the evaluation of

one or several SoP. Their type and number depend on

the algorithm chosen (Hanselmann, 1987; Istepanian

and Whidborne, 2001; Gevers and Li, 1993). For in-

stance, the direct forms require only 1 SoP, whereas

the n-th order state-space require n + 1 SoPs.

The products considered in such a SoP are prod-

ucts of real constants and real variables. But, in the

context of ﬁxed-point design, only ﬁxed-point vari-

ables and ﬁxed-point constants are considered. In this

article, we consider SoPs whose constants have al-

ready been converted in FxP format.

More formally, we consider SoPs

s =

∑

i=1

· v

, (6)

where {c

}

16i6n

are given non-null FxP constants

and {v

}

16i6n

FxP variables only known to be in

known intervals [v

]. We focus on the best way

(i.e. employing the minimum word-lengths) to obtain

a rounding of the exact sum s at a given format.

Remark 2. It is also possible to consider the {c

}

to be real constants instead of FxP constants, so as

to analyze the impact of their quantization that is not

considered here.

However, this impact is well studied with sensitiv-

ity measures such as the transfer function sensitivity

(Tavs¸ano

glu and Thiele, 1984; Gevers and Li, 1993;

Hinamoto et al., 2006), the pole/zero sensitivity (Gev-

ers and Li, 1993; Li, 1998) or IIR stability (Lu and

Hinamoto, 2003).

3 BITS FORMATTING

The main point of the proposed approach is that if the

ﬁnal ﬁxed-point format of a sum s =

∑

, denoted

FPF

= (m

) is known, then it is probably possi-

ble to discard some useless bits.

More formally, this paper is focused on bits of p

with positions lower than `

(section 3.2) and greater

than m

(section 3.3) in order to determine their im-

pact on the result. We determine the useless bits

and remove them from p

s before the sum is com-

puted. The p

s are rounded into an intermediate for-

mat (m

−δ), where δ is the number of non-useless

bits with position lower than `

. Then, the sum of

these modiﬁed p

s is computed and rounded into the

ﬁnal format FPF

in order to obtain the ﬁnal result

(see Figure 2(b)).

3.1 Deﬁnitions and notations

In this section the ﬁxed-point rounding modes used in

this article are deﬁned.

Deﬁnition 1 (Fixed-point rounding modes). Let x be

a real value. The notations ◦

(x), O

(x) and M

(x)

express the rounding to the nearest, the rounding

down (i.e. truncation) and the rounding up of x ac-

cording to the d

bit, respectively. These operators

FormattingBitstoBetterImplementSignalProcessingAlgorithms

105

(a) The exact sum is performed and then rounded to

)

(b) The sum is performed on the format (m

+δ) and

then rounded to (m

)

Figure 2: Two different ways to perform the FxP accumulation.

are deﬁned by:

◦

(x) , 2

, (7)

(x) , 2

, (8)

(x) , 2

. (9)

The operator ?

(x) is the faithful rounding of x at

the d

bit, i.e.

(x) ∈ {O

(x),M

(x)}. (10)

The round-to-the-nearest operation always returns

the nearest representable point of the real exact value,

while the faithful rounding operation produces either

the nearest or next-nearest point.

Notations. Some notations need to be explicitly de-

ﬁned before explaining the proposed approach:

• p

, c

× v

denotes the result of the ﬁxed-point

product of c

and v

. According to the ﬁxed-point

multiplication rule (Lopez et al., 2012), the ﬁxed-

point format of p

is deﬁned as FPF

, (m

) =

+ m

+ 1,`

+ `

• p

i, j

is the j

bit of p

, for 1 6 i 6 n and `

6 j 6

• (M,L) is the FPF of the exact sum s =

∑

i=1

where

M , max

) +



log

(n)



(11)

and

L , min

). (12)



log

(n)



corresponds to the number of carry bits

to consider for the sum of n terms.

Moreover, three different sums are also considered,

where 

is a given common rounding mode (round-

to-nearest or truncate): 

∈ {◦

• s

, 

(s) is the rounding of the exact sum s into

the ﬁnal format FPF

• s

∑

i=1



−δ

) is the sum of the products p

rounded into format (m

−δ) where δ is a given

positive constant to be discussed later.

• s

, 

) is the rounding of the sum s

into the

ﬁnal format FPF

Figures 2(a) and 2(b) illustrate these different approx-

imation of the sum s.

Modular ﬁxed-point sum. As reminded in equa-

tion (3), a ﬁxed-point number x is coded in computer

with a w-bit signed integer X. As a consequence, all

the operations are done modulo 2

on this integer.

Proposition 1 speciﬁes the modular ﬁxed-point sum

as an extension of the modular sum on integers.

Proposition 1 (Modular ﬁxed-point sum). The sum

modulo 2

of two ﬁxed-point numbers x and y sharing

the same FPF (m,`), is noted x

⊕ y and is computed

as:

⊕y ,



(X +Y + 2

d−`

) mod 2

d−`+1



− 2

d−`



(13)

Moreover, the modular ﬁxed-point sum of n ﬁxed-

point numbers x

is noted and computed as:

16i6n

, x

⊕ x

⊕ ...

⊕ x

. (14)

Proof: The ﬁxed-point sum modulo d, x

⊕ y, corre-

sponds to the d − `-bits sum of the integers X = x.2

−`

and Y = y.2

−`

Therefore, adding two signed ﬁxed-point num-

bers requires to convert them in positive integers, add

them modulo 2

d−`+1

, and convert the result back into

signed ﬁxed-point number.

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

106

Example 1. Adding 12.5 and 3.75 in FPF (4,−3)

(two’s complement with 8 bits) is given by 12.5

⊕3.75

and leads to −15.75 according to eq. (13) because of

the overﬂow. 12.5 is coded by 01100.100

, 3.75 is

coded by 00011.110

, so the modular sum leads to

10000.010

into format (4,−3), that is interpreted as

−15.75.

3.2 LSBs Formatting

Let consider the ﬁnal FxP format (m

) of a SoP. It

appears that not all the least signiﬁcant bits are use-

full in order to correctly round the result of a SoP to

). The value δ is the position such that all bits

with a position lower than `

− δ are insigniﬁcant and

can be removed from p

s (Fig. 2(b)). Therefore, only

s such that `

< `

−δ are rounded, the other remain

unchanged. The sum s

of rounded p

s is computed

on format (m

− δ) and ﬁnally rounded onto the

ﬁnal format (m

The following proposition formalizes the choice

of δ.

Proposition 2. For both rounding mode (

= ◦

round-to-nearest or 

= O

truncation), the integer

δ that provides s

= ?

) is given by:

δ = dlog

)e (15)

with n

= Card(I

) and I

, {i | `

< `

Proof: This proof is done for truncation round-

ing mode.The same reasoning can be established for

round-to-nearest mode.

Computation of s involves all bits p

i, j

whereas s

requires only bits p

i, j

for j > 2

−δ

, so:

s > s

(16)

The trivial case s = s

implies s

= s

, so there-

after only the case s − s

> 0 is considered and the

difference s − s

is evaluated precisely as the sum of

bits p

i, j

for 1 6 i 6 n and L 6 j 6 `

− δ − 1:

s − s

∑

i=1

−δ−1

∑

j=L

i, j

(17)

Since

∑

−δ−1

j=L

i, j

< 2

−δ

for 1 6 i 6 n, s − s

can be bounded as follows:

s − s

< n

· 2

−δ

(18)

Now, the difference s

− s

corresponds to the

rounding of the difference s − s

according to the `

bit:

− s

= O

(s − s

) (19)

It also can be viewed as the carry bits greater than 2

implied by the difference s − s

Using equation (18), the difference s

− s

can

also be bounded:

b(s − s

) · 2

−`

c 6 (s − s

) · 2

−`

< n

· 2

−δ

(20)

− s

< n

· 2

−δ

(21)

Since δ needs to be determined in order to verify

− s

| 6 2

, the following inequality comes from

equation (21):

· 2

−δ

6 2

(22)

The smallest integer solving inequality (22) is δ =

dlog

)e.

Remark 3. With Proposition 2, it may happened that

one p

(or more) has a MSB lesser than `

− δ, and

so all bits of this p

will be removed by applying this

technique. Therefore, a good idea will be to redeter-

mine δ with n

minus the number of removed p

. So

equation (15) can be replaced by Algorithm 1.

Algorithm 1: Evaluation of the integer δ.

Input: Operands p

s in format (m

)

The ﬁnal format FPF

= (m

)

Output: δ ∈ N

1 n

← n;

2 repeat

3 n

← n

;

4 δ ← dlog

)e;

5 n

← Card({i | 1 6 i 6 n and m

< `

−δ});

6 until n

= n

;

7 return δ

Formating method. The ﬁrst step of LSB format-

ting is a direct application of proposition 2: it removes

useless bits. After this step `

> `

− δ,∀1 6 i 6 n.

The second step involves having `

= `

− δ,∀1 6

i 6 n. To do this, either FPF

can be changed from

) to (m

− δ) for p

s such that `

> `

− δ

(consisting to add `

−`

+δ zeros to the right of these

s), or multipliers can be rewritten to perform opera-

tion into a given word-length. Let M

be the multiplier

computing p

= c

×v

. Then, w

, the word-length of

the result of M

is given by:

= m

+ `

+ 1 (23)

with

= m

+ m

+ 1 (24)

= `

− δ (25)

where m

and m

are MSBs of c

and v

respectively.

FormattingBitstoBetterImplementSignalProcessingAlgorithms

107

Remark 4. For a better accuracy, m

can be evalu-

ated using formulas from section 2.1, it avoids double

sign bit in general case (given by the +1 in eq. (24)).

Moreover, if `

+ `

> `

, then `

+ `

− `

zeros

are added to the right of p

s to ensure `

= `

− δ for

these p

Error evaluation. Adding two numbers in FxP

arithmetic requires to align them onto the same LSB

using right-shifts. A rounding error may occur, which

introduces a numerical error. After the second step of

LSB formatting, where rounding errors may be intro-

duced, all p

s have the same LSB, i.e. `

− δ. There

is no need of right-shift to align operands of additions

and therefore no additional rounding errors are intro-

duced by the global sum of p

The total number of right-shifts involved in the

ﬁrst step of our method can be bounded as follows.

Proposition 3. With this LSB formatting technique

and for a n

-order SoP, the number of right-shifts is

bounded by n + 1, at most one right-shift by multi-

plier (denoted d

for multiplier M

) and exactly one

ﬁnal right-shift (denoted d

). Their values are:

, `

− δ − `

− `

∀i ∈ I (26)

and

, δ (27)

where I = {i | 1 6 i 6 n and `

− δ > `

+ `

Proof: d

is the right-shift in multiplier M

if a right-

shift is necessary, i.e. if `

− δ > `

+ `

so the

number of bits to remove to ensure `

= `

− δ is

− δ − `

− `

. All the additions are computed on

+ δ bits, and the result is w

bits long, so the ﬁnal

right-shift value is δ.

Remark 5. In Proposition 3 only non-zero right-

shifts are considered. If d

is deﬁned as max(`

−

δ − `

− `

,0) rather than just `

− δ − `

− `

, all

multipliers have a right-shift, possibly null, and so the

exact number of right-shifts is n + 1.

Finally, it is possible to bound the error introduced

by our method. As seen in (Hilaire and Lopez, 2013),

the right shifting of d bits of a variable x (with (m,`)

as FPF) is equivalent to add an interval error [e] =

[e;e] with

Truncation Round to the nearest

[e,e] [−2

`+d

+ 2

;0] [−2

`+d−1

+ 2

`+d−1

]

(28)

So the global interval error for the LSB technique can

be evaluated with the following properties.

Proposition 4. The global interval error using LSB

formatting technique is [e] = [e; e] with:

Truncation:

e =

∑

i∈I

(−2

+ 2

) − 2

+ 2

−δ

(29)

e = 0 (30)

Round to nearest:

e =

∑

i∈I

(−2

−1

+ 2

) − 2

−1

+ 2

−δ

(31)

e =

∑

i∈I

−1

) + 2

−1

(32)

with I = {i | 1 6 i 6 n and `

−δ > `

} and `

+ `

, where `

and `

are positions of LSBs of c

and v

respectively.

Proof: By using (28) on a multiplier i, e equals to

−2

−1

+ 2

where d

is the right-shift value given

by Proposition 3 and p

is the initial LSB of the mul-

tiplier result, i.e. the optimal LSB which is the sum

of LSBs of product operands c

and v

. For the ﬁnal

right-shift, the initial LSB equals to `

− δ and the ﬁ-

nal result is δ bits right-shifted.

Remark 6. The precise bounds of the global inter-

val error shown in Proposition 4 can be bounded by

a power of 2. Indeed, for truncation rounding mode

the global interval error is included in ] − 2

;0],

whereas for round-to-nearest rounding mode it is in-

cluded in ] − 2

In (Lopez et al., 2012), all p

s have different LSBs,

and therefore the global error depends on the order of

the additions. Consequently, all the different evalua-

tion schemes (ES), i.e. all the different possible orders

of the additions, are generated and the choice is made

meanly for ES with a minimal error. Here, all ES have

the same global error value (Proposition 4), so error

can not be a criteria to choose the best ES representing

the sum. The criteria chosen in the section 5 is the in-

ﬁnite parallelism criteria, i.e. the most parallelizable

ES.

3.3 MSBs Formatting

The MSBs of p

s having a greater positions than the

ﬁnal MSB, m

can be removed using a new formal-

ization of the Jackson’s Rule (Jackson, 1970). This

Rule states that in consecutive additions and/or sub-

tractions in two’s complement arithmetic, some inter-

mediate results and operands may overﬂow. As long

as the ﬁnal result representation can handle the ﬁnal

result without overﬂow, then the result is valid.

Example 2. Let us consider a sum S of three 8-bit in-

tegers with two’s complement arithmetic, for example

104 + 82 − 94. The result S = 92 is in the range of 8-

bit signed numbers, but the intermediate sum 104+82

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

108

produces an overﬂow and equals to −70 into this for-

mat (instead of 186 that cannot be represented). The

ﬁnal sum −70 − 94 also produces an overﬂow and

equals to 92 into the ﬁnal format, that is the correct

result.

With this paper’s notations, it means that bits with

a greater position than m

can be removed from con-

cerned p

Proposition 5 (Fixed-Point Jackson’s Rule). Let s be

a sum of n ﬁxed-point number p

s, in format (M,L).

If s is known to have a ﬁnal MSB equals to m

with

< M, then:

s =

16i6n

∑

j=L

i, j

(33)

Proof: s =

∑

i=1

, so, from (1):

s =

∑

i=1

−2

i,M

M−1

∑

j=L

i, j

(34)

All bits of s greater than 2

(from p

i, j

with j > m

1 and from the carry bits produced by p

i, j

with j <

+ 1) are repetitions of the sign bits, since −2

s < 2

(by deﬁnition of the ﬁnal FPF). Therefore, s

can be only computed with p

i, j

with j < m

+1 in the

format FPF

Thus, in our method, the MSB formatting is an

application of the propostion to a sum s

previously

LSB-formatted p

s, i.e. with L = `

− δ. Therefore,

can be computed only using bits p

i, j

with 1 6 i 6

n, `

− δ 6 j 6 m

without considering intermediate

overﬂows.

4 OUTPUT ERROR ANALYSIS

Let us consider a n-th order IIR

ﬁlter having H as a

transfer function:

H(z) =

+ b

−1

+ ··· + b

−n

1 + a

−1

+ ··· + a

−n

, ∀z ∈ C. (35)

This ﬁlter is usually realized with the following

algorithm

y(k) =

∑

i=0

u(k − i) −

∑

i=1

y(k − i) (36)

where u(k) is the input at step k and y(k) the output at

step k.

So the evaluation of the ﬁlter relies on the evalua-

tion of a SoP. As seen in previous sections, the ﬁxed-

point evaluation of eq. (36) implies the add of an error

Inﬁnite Impulse Response

u(k)

e(k)

∆y(k)

†

(k)

y(k)

Figure 3: Equivalent system, with output error extracted.

e(k) at time k, and only y

†

(the output contaminated

with roundoff error) can be computed:

†

(k) =

∑

i=0

u(k − i) −

∑

i=1

†

(k − i) + e(k). (37)

In (Lopez et al., 2012), it has been shown that the

implemented system eq. (37) can be seen as the ini-

tial system (36) with an error added on the output, as

shown in Figure 3: by subtracting equations (37) and

(36), it comes

†

(k) − y(k) = e(k)−

∑

i=1



†

(k − i) − y(k − i)



(38)

So the output error ∆y(k) , y

†

(k) − y(k) can be seen

as the result of the error e(k) through the ﬁlter H

de-

ﬁned by

(z) =

1 + a

−1

+ ··· + a

−n

, ∀z ∈ C. (39)

Since the error e(k) done in the evaluation of the

SoP is known to be in a given interval [e;e] (see

Proposition 4), then the following proposition (Hilaire

and Lopez, 2013) gives the output error interval:

Proposition 6 (Output error interval). ∆y(k) is the

output of the error e(k) through the ﬁlter H

. If the

error e(k) is in [e; e], then ∆y(k) is in [∆y; ∆y] with:

∆y =

e + e

−

e − e

∞

(40)

∆y =

e + e

e − e

∞

(41)

and

is the DC-gain (low-frequency gain) of H

and

∞

its worst-case peak gain:

∞

sup

k>0

|y(k)|

sup

k>0

|u(k)|

∀u and y input and output of H

(42)

They can be computed by:

= H

(1),

∞

∑

k>0

(k)| (43)

where h

(k) is impulse response of the ﬁlter H

Proof: Since H

is linear, ∆y(k) can be seen as the

sum of a constant term

e+e

through the ﬁlter H

and

a variable term bounded by

e−e

. The constant term is

ampliﬁed by the low-frequency gain

, whereas

the bound of the variable term is ampliﬁed by

∞

(eq. (42)).

FormattingBitstoBetterImplementSignalProcessingAlgorithms

109

= 0

= dlog

= min

)

Figure 4: Bits representation of the sum of the example.

5 RESULTS AND COMPARISONS

A 4-th order Butterworth ﬁlter is used as an illustra-

tive example. The chosen realization to compute this

ﬁlter is the Direct Form I:

y(k) =

∑

i=0

u(k − i) −

∑

i=1

y(k − i). (44)

Its coefﬁcients a

s and b

s are given by the Matlab

command butter(4,0.136):

= 0.001328017792779

= −2.871116228316502 b

= 0.005312071171115

= 3.208250066295749 b

= 0.007968106756673

= −1.634594881084453 b

= 0.005312071171115

= 0.318709327789667 b

= 0.001328017792779

For implementations, the output variables y(i)s,

input variables u(i)s, constants a

s and b

s are 16-bit

words.

Moreover, variables u(i)s are consid-

ered in this example to be in the interval

[−13;13] (the corresponding FPF is (4,−11)),

and variables y(i)s (including result out-

put y(k)) are known to be in the interval

[−17.123541221107534;17.123541221107534]

(corresponding to the ﬁnal FPF (m

) = (5,−10)).

From these informations, the operands to be

summed, p

s, can be obtained with their respective

FPF:



i−1

u(k − (i − 1)) if 1 6 i 6 5

i−5

y(k − (i − 5)) if 6 6 i 6 9

FPF

= (−4, −35)

FPF

= (−2, −33) FPF

= (8, −23)

FPF

= (−1, −32) FPF

= (8, −23)

FPF

= (−2, −33) FPF

= (7, −24)

FPF

= (−4, −35) FPF

= (5, −26)

Four implementations are compared: a double

precision implementation and three ﬁxed-point imple-

mentations using bit formatting approach using dif-

ferent values of δ. In the ﬁrst FxP implementation

(denoted Fix

), all bits are considered. This means

that δ

is chosen such that `

− δ

= min

). In other

word, we have δ

= `

− min

) = 25. The Fix

im-

plementation corresponds to the computation of the

sum s with no LSB formatting.

In the second FxP implementation Fix

, no addi-

tional bits are considered. The intermediate format

is the ﬁnal format, (m

), which corresponds to

= 0. A large LSB reduction is performed.

The third FxP implementation Fix

is the faithful

implementation, with δ

determined from Proposition

2, i.e. δ

= dlog

)e with n

= n = 9, so δ

= 4.

Only 4 guards bits are used in the LSB formatting.

Figure 4 illustrates this example. For Fix

, since

the intermediate format is (5,−35), additional bits

equal to 0 are considered to align all p

s onto this

format. For Fix

and Fix

, the intermediate formats,

(5,−10) and (5,−14) respectively, permit to remove

bits, blue and green hatched bits and blue hatched

bits respectively. Finally, the intermediate sums are

rounded to the ﬁnal format (5,−10), except s

which

is already in the ﬁnal format.

The global interval error [e;e] is computed, for the

implementation Fix

, using Proposition 4 :

e = −1.4645302 × 10

−3

, e = 0. (45)

From equation (43), DC-gain and worst-case peak

gain of H

are obtained :

= 49.5647,

∞

= 66.8474. (46)

Finally, the output error interval (Proposition 6)

[∆y;∆y] is computed from equations (45) and (46) :

∆y = −8.52445240×10

−2

, ∆y = 1.26555189×10

−2

(47)

As illustration (but not proof), of the theoretical

result (46), a simulation in FxP and ﬂoating point

arithmetic has been done with a white noise input u(k)

in [−13; 13]. The error between the double ﬂoating re-

sult and each of the FxP implementations is shown in

Figure 5.

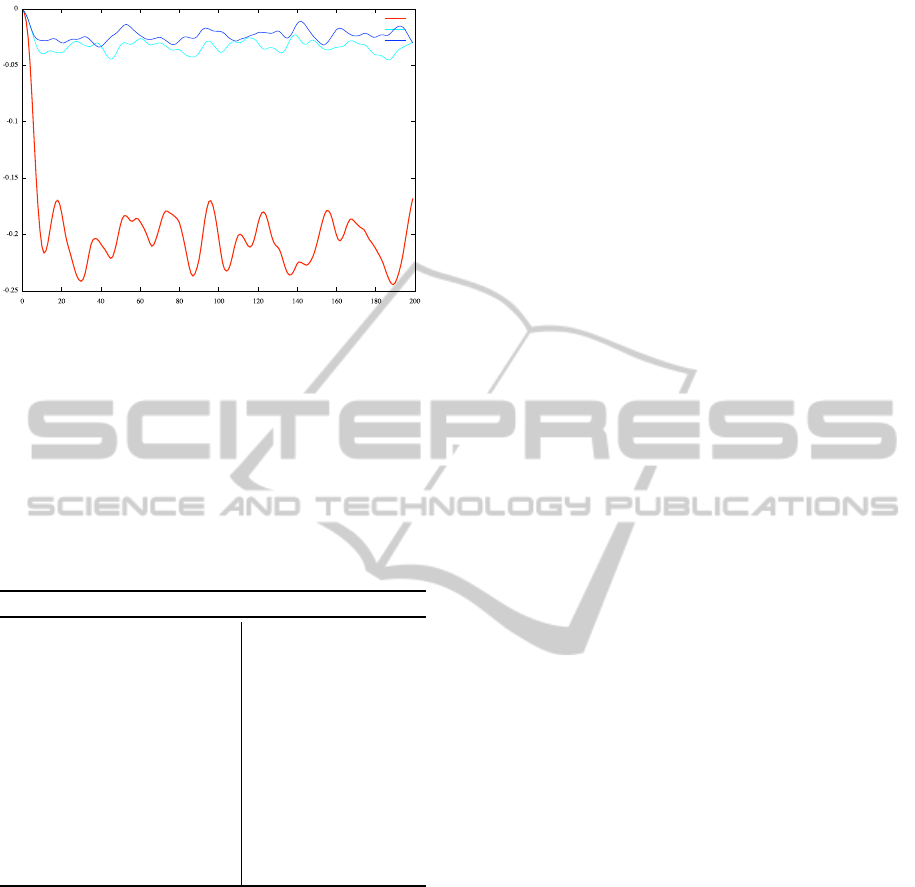
The number of additional bits considered in Fix

is small compared with Fix

which considers all bits,

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

110

Fix

Figure 5: Computed error between double implementation

and the three different ﬁxed-point implementations.

but it is good enough to have errors measures far bet-

ter than Fix

and really close to Fix

. The plotted er-

ror for implementation Fix

is in the bound predicted

by the theory.

The ﬁxed-point implementation Fix

is given by

algorithm 2. In this implementation, sum modulo

(i.e. 2

) is performed, but since algorithm

considers integer computations, the sum is performed

modulo 2

+1−`

+δ

(i.e. 2

Algorithm 2: Fixed-point algorithm.

Input:

U0 to U4: 16-bit input (4, −11)

Y 1 to Y 4: 16-bit input (5,−10)

Output: Y : 16-bit output (5,−10)

Data: Rx: 20-bit registers

⊕: the 20-bit sum

R0 ← (23520 ∗Y1)  9;

R1 ← (−26282 ∗Y2)  9;

R2 ← R0 ⊕ R1;

R0 ← (22280 ∗U0)  21;

R1 ← R0 ⊕ R2;

R0 ← (22280 ∗U3)  19;

R2 ← (−20887 ∗Y4)  12;

R3 ← R0 ⊕ R2;

R0 ← R1 ⊕ R3;

R1 ← (22280 ∗U4)  21;

R2 ← (26781 ∗Y3)  10;

R3 ← R1 ⊕ R2;

R1 ← (16710 ∗U2)  18;

R2 ← R3 ⊕ R1;

R1 ← (22280 ∗U1)  19;

R3 ← R2 ⊕ R1;

R1 ← R0 ⊕ R3;

// Output computation

Y ← R1  4;

6 CONCLUSIONS

Throughout this paper, a new method of formatting

bits has been described, in order to design ﬁxed-point

sum-of-products and then linear ﬁlters. This method

allows to remove some bits and keep only the bits that

impact the ﬁnal result. The computed result is a faith-

ful rounding of the ﬁnal result considering all the bits.

The example has shown the utility of applying this

method to a linear ﬁlter expressed in a very common

form, and the gain in term of number of bits is signif-

icant.

Future work will consist of a word-length opti-

mization step that will consider the bit formatting

method, and a code generation for algorithm-to-code

mapping.

ACKNOWLEDGEMENTS

This work has been sponsored by french ANR agency

under grant No ANR-11-INSE-008.

The authors would like to thank Florent de

Dinechin for the instructive discussions about ﬁxed-

point implementation.

REFERENCES

Constantinides, G., Cheung, P., and Luk, W. (2004). Syn-

thesis and Optimization of DSP Algorithms. Kluwer

Academic Publishers.

Gevers, M. and Li, G. (1993). Parametrizations in Control,

Estimation and Filtering Probems. Springer-Verlag.

Hanselmann, H. (1987). Implementation of digital con-

trollers - a survey. Automatica, 23(1):7–32.

Hilaire, T. and Lopez, B. (2013). Reliable implementation

of linear ﬁlters with ﬁxed-point arithmetic. In Proc.

IEEE Workshop on Signal Processing Systems (SiPS).

Hinamoto, T., Omoifo, O., and Lu, W.-S. (2006). L2-

sensitivity minimization for mimo linear discrete-time

systems subject to l2-scaling constraints. In Proc. IS-

CCSP 2006.

Istepanian, R. and Whidborne, J., editors (2001). Digital

Controller implementation and fragility. Springer.

Jackson, L. (1970). Roundoff-noise analysis for ﬁxed-

point digital ﬁlters realized in cascade or parallel form.

Audio and Electroacoustics, IEEE Transactions on,

18(2):107–122.

Li, G. (1998). On the structure of digital controllers with

ﬁnite word length consideration. IEEE Trans. on Au-

tom. Control, 43(5):689–693.

Lopez, B., Hilaire, T., and Didier, L.-S. (2012). Sum-of-

products Evaluation Schemes with Fixed-Point arith-

metic, and their application to IIR ﬁlter implementa-

tion. In Conference on Design and Architectures for

Signal and Image Processing (DASIP).

Lu, W.-S. and Hinamoto, T. (2003). Optimal design of

iir digital ﬁlters with robust stability using conic-

quadratic-programming updates. In IEEE Trans. Sig-

nal Processing, volume 51, pages 1581–1592.

Padgett, W. T. and Anderson, D. V. (2009). Fixed-point

signal processing. Synthesis Lectures on Signal Pro-

cessing, 4(1):1–133.

Tavs¸ano

glu, V. and Thiele, L. (1984). Optimal design of

state-space digital ﬁlters by simultaneous minimiza-

tion of sensibility and roundoff noise. In IEEE Trans.

on Acoustics, Speech and Signal Processing, volume

CAS-31.

FormattingBitstoBetterImplementSignalProcessingAlgorithms

111