Persistent Spectral Hole-Burning by Two Pulses of Arbitrary
Duration
Inna Rebane
Institute of Physics, University of Tartu, Riia 142, 51014 Tartu, Estonia
Keywords: Spectral Hole-burning by Pulses, Perturbation Theory, Spectral Hole Narrowing.
Abstract: Two-step spectral hole-burning are considered in the cases of three- and four-level systems and an arbitrary
duration of burning pulses. The shapes of the spectral holes (more exactly – the spectral hole-burning
efficiencies that determined them) in inhomogeneous distribution functions of the centers over the transition
frequencies of the first and the second steps are calculated. It is shown that with increasing the time delay
between pulses the widths of the spectral holes in the inhomogeneous distribution function corresponding to
the absorption of the pulses on end at the first step of this process decrease. This phenomenon does not
depend on the duration of the second burning pulse and is absent at the second step of the process.
1 INTRODUCTION
The inhomogeneous broadening of the spectra of the
electronic transitions in the impurity systems can be
eliminated by using a method of the spectral hole-
burning (SHB) (Kharlamov, Personov and
Bykovskaya, 1974; Gorokhovskii, Kaarli and
Rebane LA, 1976; Moerner, 1988). The first
experimental works on the two-step SHB in the
three- (Winnacker, Shleby and Macfarline, 1985)
and the four-level (Friedrich and Haarer, 1984; Lee,
Gertz, Marinero and Moerner, 1985) systems were
published about 25 years ago. The spectral holes in
the inhomogeneous distribution functions (IDF) are
determined through SHB efficiencies (Rebane LA,
Gorokhovskiy and Kikas, 1982) (e.g. exponentially
or linearly). In this work we use the second and the
third orders of the perturbation theory for calculating
SHB efficiencies in the three- and four-level systems
correspondingly; the durations of the pulses are
arbitrary and computer calculations are done.
2 SHB EFFICIENCIES
The electronic levels are described by the rates of
the energy relaxation γ
0
, γ
1
, γ
1’
, and γ
2
. The first pulse
with arbitrary duration is applied between the levels
0 and 1 and the second pulse with arbitrary duration
is applied between the levels 1 and 2 (for the three-
level system) or the levels 1’ and 2 (for the four-
level system) (Figure 1). The inhomogeneous
distributions of the frequencies Ω
01
and Ω
12
(for the
three-level system) or Ω
1’2
(for the four-level
system) of the transitions 0 → 1 and 1 → 2 (for the
three-level system) or 1’ → 2 (for the four-level
system) are taken into account.
SHB efficiencies P
3
(Ω
01
, Ω
12
, t) and P
4
(Ω
01
, Ω
1’2
,
t) at sufficiently small excitation intensities can be
considered in the second and the third orders of the
perturbation theory,
11
''
30112 1 1211
'
2212231122
(,,) ' '(,')
'(,')(',,',,'),
ttt
tt
P t dt dt dt S t t
dt dt S t t F t t t t t

  
 
 



(1)
11 22
''
4011'2 1 1211
''
222233133
4112233
(, ,) ' '(,')
'(,') '(,')
(', ,', ,', ,').
ttt
tt tt
P t dt dt dt S t t
dt dt G t t dt dt S t t
Fttt tt tt

  
   
 



 
(2)
In (1) and (2) α is the photochemical quantum yield,
F
3
and F
4
are the correlation functions of the three-
level and the four-level systems, S
1
and S
2
are the
correlation functions of the first and the second
pulses. The correlation function G in (2) describes
79
Rebane I..
Persistent Spectral Hole-Burning by Two Pulses of Arbitrary Duration.
DOI: 10.5220/0004707100790082
In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 79-82
ISBN: 978-989-758-008-6
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

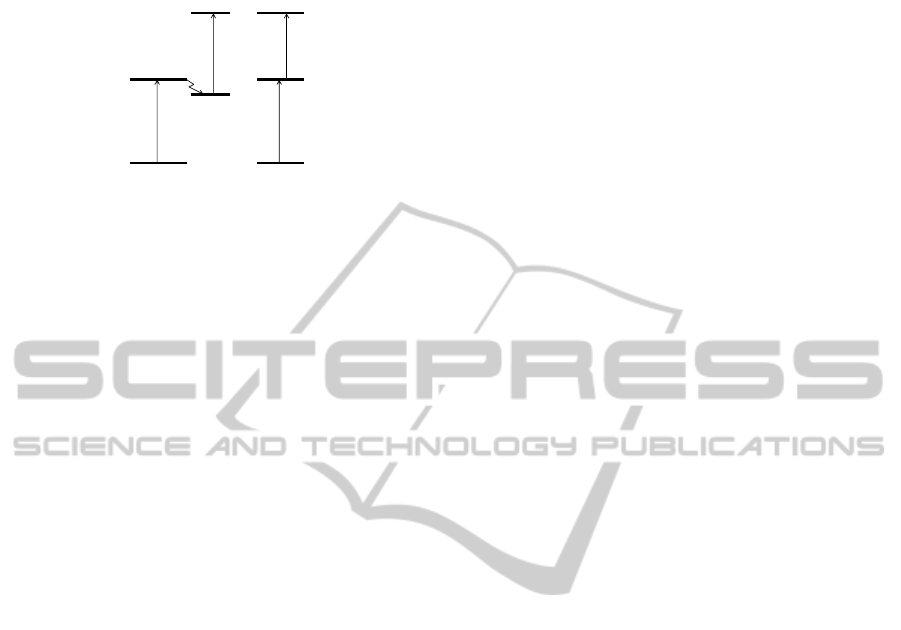
the relaxation processes from the level 1 to the level
1’ in the four-level system.
0
1
1’
2
0
1
2
AB
Figure 1: Scheme of SHB in the four- (A) and the three-
level (B) systems by the pulses.
We use the following correlation functions for
exciting pulses:
13 3 3 1 3 1 1 13 3
13 3 1
21 1 1 2 1 2 2 21 1
21 1 2
( , ' ) ( ) ( ' ) exp[ ( '
('2)/2],
( , ' ) ( ) ( ' ) exp[ ( '
('2)/2]
Stt t t i t t
tt
Stt t t i t t
tt

  

  

  
  
  
  
(3)
(the pulses are coherent and of a single-sided
exponential shape) where ω
1
and ω
2
are the
frequencies of the maximums, and Δ
1
and Δ
2
are the
fwhm spectral widths of the pulses, τ
1
and τ
2
are the
time moments when the pulses begin to pass through
the impurity centre.
The correlation functions of the three- and the
four-level systems are the following:
31122 3 2 11
12 1 1 1 1 1 2 2
01 2 2 0 2 2
(', ,', ,') exp[ (2' ')/2
(')(' ')/2
(')(')/2],
Fttt t t C t t t
itt tttt
itt tt




     
   
(4)
4112233 4
211 1'211
1' 1 1 2 2 11' 2 2
12 2 3 3 013 3
03 3
(', ,', , ', ,')
exp[ (2 ' ' ) / 2 ( ' )
(' ')/2 (')
(' ')/2 (')
(')/2],
Fttt tt tt C
tt t i t t
tt tt i tt
tt tt i tt
tt





  
 
 

(5)
where C
3
and C
4
are constants. In the correlation
function
22 1 1 1 1
11 1
(,') ( )(' )
exp[ ( ' 2 ) / 2]
Gt t t t g
gt t

 

 

(6)
the parameter g describes the rate of the energy
transfer from the level 1 to the level 1’.
IDF ρ
3
(Ω
01
, Ω
12
, t) (or ρ
4
(Ω
01
, Ω
1’2
, t)) takes into
account the inhomogeneous distribution of the
frequencies and under certain assumptions changes
exponentially with time (Rebane LA, Gorokhovskiy
and Kikas, 1982),
30112 300112 30112
(,,) (, )exp[(,,)],tPt      
(7)
4 01 1' 2 40 01 1' 2 4 01 1' 2
(, ,) (, )exp[(, ,)].tPt      
(8)
Here ρ
30
(ρ
40
) is the inhomogeneous distribution
function before the beginning of SHB, whereas the
regions of the frequencies Ω
01
and Ω
12
(Ω
1’2
) do not
overlap. Under small irradiation doses
3 01 12 30 01 12 3 01 12
(,,) (, )[1 (,,)],tPt     
(9)
4 01 1' 2 40 01 1' 2 4 01 1'2
(, ,) (, )[1 (, ,)].tPt     
(10)
The final spectral holes we get at t →∞:
P
3
(Ω
01
, Ω
12
) ≡ lim
t
→∞
P
3
(Ω
01
, Ω
12
, t) (11)
and
P
4
(Ω
01
, Ω
1’2
) ≡ lim
t
→∞
P
4
(Ω
01
, Ω
1’2
, t). (12)
3 RESULTS
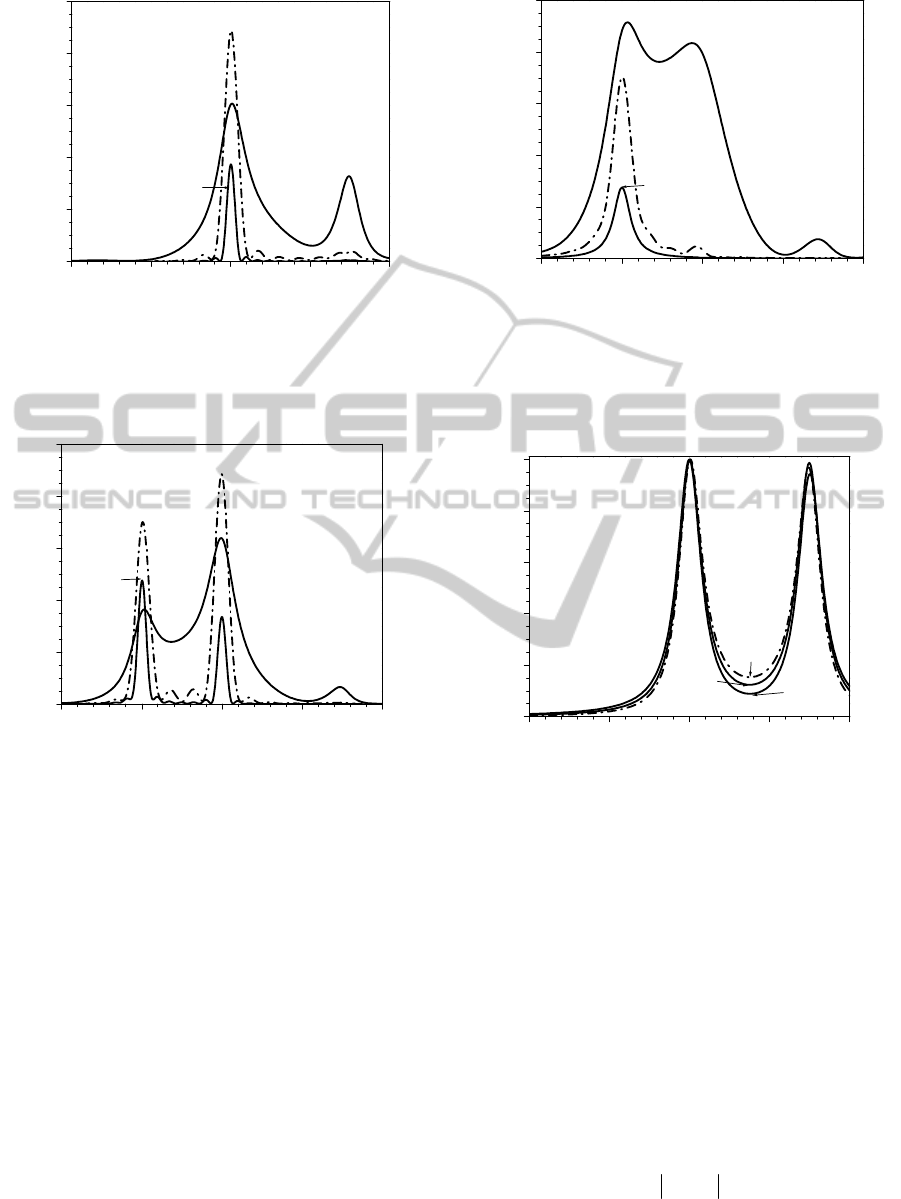
In Figure 2, SHB efficiency P
3
(Ω
01
) for the fixed
value of Ω
12
– ω
2
is calculated for different values of
the time delay T = τ
2
- τ
1
between the pulses. With
increasing the time delay T, the spectral line with the
maximum at Ω
01
= ω
1
monotonously narrows down.
The spectral line with the maximum at Ω
01
- ω
1
=
15γ
1
corresponds to absorption of both the pulses at
the same time. This spectral line appears only when
the pulses overlap, i.e. at T = 0.5γ
1
-1
, and also little
bit at T = 2.5γ
1
-1
.
For the four-level system with the same
parameters as in Figure 2, SHB efficiency P
4
(Ω
01
) is
calculated in Figure 3. In the case of Ω
11’
= -10γ
1
the
third spectral line appears with the maximum at Ω
01
- ω
1
= -10γ
1
. With increasing the time delay T
between the pulses the same monotonous narrowing
of both the spectral lines takes place. In Figure 4 the
parameter g = 2γ
1
, unlike Figure 3 where g = 0,
which leads to result that in Figure 4 the spectral line
with the maximum at Ω
01
- ω
1
= -10γ
1
is larger than
in Figure 3. Differently from Figure 3, in Figure 4
the spectral line with maximum at Ω
01
= ω
1
is
already small in the case of the time delay T = 2.5γ
1
-
1
and is absent at T = 4.5γ
1
-1
. The spectral lines
monotonously narrow down with increasing the time
delay but at T = 4.5γ
1
-1
the width of the spectral line
with the maximum at Ω
01
- ω
1
= -10γ
1
is larger than
in Figure 3.
In Figure 5, SHB efficiency P
3
(Ω
12
) for the fixed
value of Ω
01
– ω
1
is calculated. The shape of the
curve of this SHB efficiency changes a little at
different values of the time delay T, only the
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
80

-20 -10 0 10 20
0.0
0.2
0.4
0.6
0.8
1.0
3
2
1
P
3
(


) [Arbitrary units]
( 
01
- 
1
)/ 
1
Figure 2: SHB efficiency in the three-level system P
3
(Ω
01
)
for the fixed value of Ω
12
– ω
2
= -15γ
1
at the different time
delays T between the pulses: 1 – T = 0.5γ
1
-1
, 2 – T = 2.5γ
1
-
1
, 3 – T = 4.5γ
1
-1
. γ
0
= 0.01γ
1
, γ
2
= 1.5γ
1
, Δ
1
= Δ
2
= γ
1
.
-20 -10 0 10 20
0.0
0.2
0.4
0.6
0.8
1.0
3
2
1
P
4
(


) [Arbitrary units]
( 
01
- 
1
)/ 
1
Figure 3: SHB efficiency in the four-level system P
4
(Ω
01
)
for the fixed value of Ω
1’2
– ω
2
= -25γ
1
at the different time
delays T between the pulses: 1 – T = 0.5γ
1
-1
, 2 – T = 2.5γ
1
-
1
, 3 – T = 4.5γ
1
-1
. γ
0
= 0.01γ
1
, γ
1’
= 0.5γ
1
, γ
2
= 1.5γ
1
, Δ
1
= Δ
2
= γ
1
, g = 0.001γ
1
, Ω
11’
= -10γ
1
.
intensities of SHB efficiency are different at
different T. In the case of the four-level system
(Figure 6) the line of the absorption of two pulses
together with the maximum at Ω
1’2
– ω
2
= 15γ
1
appears only at the time delay T = 0.5γ
1
-1
, the shape
of the spectral line with the maximum at Ω
1’2
= ω
2
does not change.
Thus, taking into account (9) and (10), we can
say that at the first step of SHB process monotonous
narrowing of the spectral hole in IDF takes place
when the time delay T between the pulses increases.
In this process the shape of the correlation function
S
1
of the first pulse is important.
-20 -10 0 10 20
0.0
0.2
0.4
0.6
0.8
1.0
3
2
1
P
4
(


) [Arbitrary units]
(
0
1
- 
1
)/
1
Figure 4: SHB efficiency in the four-level system P
4
(Ω
01
)
for the fixed value of Ω
1’2
– ω
2
= -25γ
1
at the different time
delays T between the pulses: 1 – T = 0.5γ
1
-1
, 2 – T = 2.5γ
1
-
1
, 3 – T = 4.5γ
1
-1
. γ
0
= 0.01γ
1
, γ
1’
= 0.5γ
1
, γ
2
= 1.5γ
1
, Δ
1
= Δ
2
= γ
1
, g = 2γ
1
, Ω
11’
= -10γ
1
.
-20 -10 0 10 20
0.0
0.2
0.4
0.6
0.8
1.0
3
1
2
P
3
(

12
)[Arbitrary units]
(
12
- 
2
)/
1
Figure 5: SHB efficiency in the three-level system P
3
(Ω
12
)
for the fixed value of Ω
01
– ω
1
= -15γ
1
at the different time
delays T between the pulses: 1 – T = 0.5γ
1
-1
, 2 – T = 2.5γ
1
-
1
, 3 – T = 4.5γ
1
-1
. γ
0
= 0.01γ
1
, γ
2
= 1.5γ
1
, Δ
1
= Δ
2
= γ
1
. Here
the curve 2 is enlarged 8.55 times and the curve 3 is
enlarged 72.1 times.
In (Rebane IK, 1988) and (Rebane I, 2012) for
the three- and the four-level systems
correspondingly the same effect in the case of the
extremely short second pulse (δ-pulse) was
calculated analytically. The widths of these holes
can be narrower than the width of the hole
obtainable in one-step SHB processes by
monochromatic light in two-level systems (so-called
compensation effect). In the case where S
1
was
defined by (3) for the spectral hole width we receive
011 1
lim ( ) .
T
T 



(13)
PersistentSpectralHole-BurningbyTwoPulsesofArbitraryDuration
81

-20 -10 0 10 20
0.0
0.2
0.4
0.6
0.8
1.0
3
2
1
P
4
(
1'2
)[Arbitrary units]
( 
1'2
- 
2
)/ 
1
Figure 6: SHB efficiency in the four-level system P
4
(Ω
1’2
)

for the fixed value of Ω
01
– ω
1
= -25γ
1
at the different time
delays T between the pulses: 1 – T = 0.5γ
1
-1
, 2 – T = 2.5γ
1
-
1
, 3 – T = 4.5γ
1
-1
. γ
0
= 0.01γ
1
, γ
1’
= 0.5γ
1
, γ
2
= 1.5γ
1
, Δ
1
= Δ
2
= γ
1
, g = 0.001γ
1
, Ω
11’
= -10γ
1
.
In (Rebane IK, 1988) the model with both rates
of the relaxation of the first electronic level, the
energy (γ
1
) and the pure phase (Γ
1
) was used. This
model showed that the width conditioned by the
pure phase relaxation Γ
1
adds to the spectral hole
width σ without taking into account Γ
1
.
In (Rebane IK, Tuul and Hizhnyakov, 1979) the
analogical effect of the line narrowing was
considered in the time depending resonant secondary
emission (consists of the scattering and of the
ordinary and the hot luminescence).
4 CONCLUSIONS
Computer calculations are carried out for the two-
step SHB in the three- and four-level systems by
light pulses of the arbitrary duration. In the three-
level system we receive two spectral lines of SHB
efficiency P
3
(Ω
01
) at the first step of this process (for
fixed value of Ω
12
– ω
2
) or of SHB efficiency
P
3
(Ω
12
) at the second step of this process (for fixed
value of Ω
01
– ω
1
). In the four-level system we
receive the three spectral lines of SHB efficiency
P
4
(Ω
01
) (for fixed value of Ω
1’2
– ω
2
) or of SHB
efficiency P
4
(Ω
1’2
) (for fixed value of Ω
01
– ω
1
). The
calculations show that at the first step of SHB with
increasing the time delay T between pulses, the
spectral lines of SHB efficiencies P
3
(Ω
01
) and
P
4
(Ω
01
) corresponding to the absorption of the pulses
on end and due to these the corresponding spectral
holes in IDF monotonously narrow down. This
phenomenon does not depend on the duration of the
second burning pulse and is absent for the spectral
lines corresponding to the absorption of the two
pulses together and also at the second step of the
process.
ACKNOWLEDGEMENTS
This work was supported by the European Union
through the European Regional Development Fund
(Centre of Excellence "Mesosystems: Theory and
Applications", TK114).
REFERENCES
Friedrich, J., D. Haarer, D., 1984. Photochemical hole
burning – a spectroscopic study of relaxation
processes in polymers and glasses. Angewandte
Chimie International Edition. 23, 113-140.
Gorokhovskii, A. A., Kaarli, R. K., Rebane, L. A., 1976.
The homogeneous pure electronic linewidth in the
spectrum of a H
2
-phthalocyanine solution in n-octane
at 5K. Optics Communications. 16, 282-284.
Kharlamov, B. M., Personov, R. I., Bykovskaya, L. A.,
1974. Stable "gap" in absorption spectra of solid
solutions of organic molecules by laser irradiation.
Optics Commununications. 12, 191-193.
Lee, H. W. H., Gertz, M., Marinero, E. E., Moerner, W.
E., 1985. 2-color, photon-gated spectral hole-burning
in an organic material. Chem. Phys. Letters. 118, 611-
616.
Moerner, W. E. (Ed.), 1988. Persistent spectral hole-
burning: science and applications. Springer-Verlag.
Berlin, Heidelberg.
Rebane, I. K., Tuul, A. L., Hizhnyakov, V. V., 1979.
Transient quasilinear spectra of resonant secondary
emission. Sov. Phys. JETP. 50, 655-660.
Rebane, I. K., 1988. Theory of two-step spectral hole
burning by pulses. Phys. Stat. Solidi (b), 145, 749-757.
Rebane, I., 2012. Theory of two-step spectral hole-burning
in four-level systems (vol 76, pg 225, 1990). Optics
Communication. 285, 3995-3996.
Rebane, L. A., Gorokhovskiy, A. A., Kikas, J. V., 1982.
Low-temperature spectroscopy of organic-molecules
in solids by photochemical hole burning. Appl. Phys.
B. 29, 235-250.
Winnacker, A., Shleby, R. M., Macfarlane, R. M., 1985.
Photon-gated hole burning – a new mechanism using
2-step photoionization. Optics Letters. 10, 350-352.
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
82