An Order-invariant Time Series Distance Measure

Position on Recent Developments in Time Series Analysis

Stephan Spiegel and Sahin Albayrak

DAI-Lab, Technische Universit¨at Berlin, Ernst-Reuter-Platz 7, 10587 Berlin, Germany

Keywords:

Time Series, Distance Measure, Recurrence Plots.

Abstract:

Although there has been substantial progress in time series analysis in recent years, time series distance

measures still remain a topic of interest with a lot of potential for improvements.

In this paper we introduce a novel Order Invariant Distance measure which is able to determine the

(dis)similarity of time series that exhibit similar sub-sequences at arbitrary positions. Additionally, we

demonstrate the practicality of the proposed measure on a sample data set of synthetic time series with

artiﬁcially implanted patterns, and discuss the implications for real-life data mining applications.

1 INTRODUCTION

The distance between time series needs to be care-

fully deﬁned in order to reﬂect the underlying

(dis)similarity of such data. This is particularly desir-

able for similarity-based retrieval, classiﬁcation, clus-

tering, segmentation and other mining procedures of

time series (Ding et al., 2008).

The choice of time series distance measure de-

pends on the invariance required by the domain

(Batista and Wang, 2011). Recent work has intro-

duced techniques designed to efﬁciently measure sim-

ilarity between time series with invariance to (vari-

ous combinations of) the distortions of warping, uni-

form scaling, offset, amplitude scaling, phase, oc-

clusions, uncertainty and wandering baseline (Batista

and Wang, 2011).

In this study we propose a novel Order-Invariant

Distance (OID) measure which is able to determine

the (dis)similarity of time series that exhibit simi-

lar sub-sequences at arbitrary positions. We claim

that order invariance is an important consideration for

domains such as automotive engineering and smart

home environments, where multiple sensors log con-

textual patterns in their naturally occurring order, and

time series are compared to discriminate complex sit-

uations (Spiegel et al., 2011a; Spiegel et al., 2011b).

To ensure the validity of our claim, we demonstrate

the practicability and capabilities of the introduced

OID measure on a sample data set of synthetic time

series with artiﬁcially implanted pattens.

The rest of the paper is structured as followed.

Section 2 presents popular distance measures which

are frequently used to compare time series. Known

invariance and important considerations for the de-

sign of time series distance measures are discussed in

Section 3. Our proposed Order-Invariant Distance is

introduced in Section 4. The capabilities of our pre-

sented OID measure are demonstrated in Section 5.

Finally we conclude the paper in Section 6.

2 DISTANCE MEASURES

Suppose we have two time series, Q and C, of length

n. To measure their similarity, we can use the Eu-

clidean Distance (ED):

ED(Q,C) =

∑

i=1

− c

)

(1)

While ED is a simple measure, it is suitable for

many problems (Lin et al., 2004). Nevertheless, in

many domains the data is distorted in some way, and

either the distortion must be removed before using

Euclidean Distance, or a more robust measure must

be used instead (Batista and Wang, 2011).

Dynamic Time Warping (DTW) allows a more in-

tuitive distance measure for time series that have sim-

ilar shape, but are not aligned in time (Keogh and

Ratanamahatana, 2005). To align two sequences us-

ing DTW we construct a matrix which contains the

distances between any two points. A warping path

264

Spiegel S. and Albayrak S..

An Order-invariant Time Series Distance Measure - Position on Recent Developments in Time Series Analysis.

DOI: 10.5220/0004165602640268

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 264-268

ISBN: 978-989-8565-29-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

W = w

.. . w

is a contiguous set of matrix elements

that deﬁnes a mapping between Q andC under several

constrains (Keogh and Ratanamahatana, 2005):

DTW(Q,C) = min



∑

k=1

(2)

This path can be found using dynamic program-

ming to evaluate the following recurrence which de-

ﬁnes the cumulative distance γ(i, j) as the distance

d(i, j) found in the current cell and the minimum

of the cumulative distances of the adjacent elements

(Keogh and Ratanamahatana, 2005):

γ(i, j) = d(q

) + min{γ(i− 1, j − 1),

γ(i− 1, j),

γ(i, j − 1)}

(3)

The Euclidean Distance between two sequences

can be seen as a special case of DTW where both time

series have same length and the warping path com-

plies with the main diagonal of the distance matrix.

However, the superiority of DTW over ED has been

demonstrated by several authors (Ding et al., 2008;

Keogh, 2003) for many data mining applications.

3 KNOWN INVARIANCE

Important considerations regarding time series dis-

tance include amplitude invariance and offset in-

variance (Batista and Wang, 2011). If we try to com-

pare two time series measured on different scales they

will not match well, even if they have similar shapes.

Similarly, even if two time series have identical am-

plitudes, they may have different offsets. To measure

the true underlying similarity we must ﬁrst center and

scale the time series (by trivial z-normalization).

Furthermore, local scaling invariance or rather

warping invariance (Batista and Wang, 2011) should

be taken into account when comparing time series.

This invariance is necessary in almost all biological

signals, which match only when one is locally warped

to align with the other. Recent empirical evidence

strongly suggests that Dynamic Time Warping is a

robust distance measure which works exceptionally

well (Ding et al., 2008).

In contrast to the localized scaling that DTW deals

with, in many data sets we must account for uniform

scaling invariance (Batista and Wang, 2011), where

we try to match a shorter time series against the pre-

ﬁx of a longer one. The main difﬁculty in creating

uniform scaling invariance is that we typically do not

know the scaling factor in advance, and are thus con-

demned to testing all possibilities within a given range

(Keogh, 2003).

Phase invariance (Batista and Wang, 2011) is im-

portant when matching periodic time series such as

heart beats. By holding one time series ﬁxed, and

testing all circular shifts of the other, we can achieve

phase invariance.

In domains where a small sub-sequence of a time

series may be missing we must consider occlusion

invariance (Batista and Wang, 2011). This form of

invariance can be achieve by selectively declining to

match subsections of a time series. However, most

real-life problems require multiple invariance.

4 ORDER-INVARIANT DISTANCE

This paper introduces an Order-Invariant Distance

(OID) measure which is able to determine the

(dis)similarity of time series which have different

shapes, but exhibit similar sub-sequences in arbi-

trary order. For example, we can imagine the speed

recorded during two different car drives, from home

to the convenience store and back, where the signals

exhibit the same location-dependent trafﬁc situations

(e.g. crosswalk, intersection, driveway, trafﬁc light)

in reverse order (refer to Figure 1) and are therefore

similar in regard of order invariance.

Although order invariance may be an important

consideration for other real-life data mining applica-

tions, relevant literature (Batista and Wang, 2011) is

lacking a time series distance measure which is able

to determine the (dis)similarity of signals that contain

multiple similar events at arbitrary positions in time.

Commonly used measures like ED and DTW are not

designed to deal with order invariance, because they

discriminate time series according to their shapes and

fail to recognize cross-alignments between unordered

sub-sequences. To this end, we developed an Order

Invariant Distance measure which matches similar

sub-sequences regardless of their order or location.

Our proposed OID measure is based on the Cross

Recurrence Plot (CRP) approach (Marwan, 2008;

Marwan et al., 2007) which tests for occurrences of

similar states in two different systems, or rather time

series (with same physical units). The data length of

both time series can differ, leading to a non-square

recurrence matrix R:

i, j

= Θ(ε− ||q

− c

||)

(4)

where Θ represents the Heaviside function (i.e.

Θ(x) = 0 if x < 0, and Θ(x) = 1 otherwise), || · || is a

norm (i.e. L

-norm) and ε is a threshold distance that

determines the radius of the similarity neighborhood.

A closer inspection of the Cross Recurrence Plot

(matrix R) reveals small-scale structures, which can

AnOrder-invariantTimeSeriesDistanceMeasure-PositiononRecentDevelopmentsinTimeSeriesAnalysis

265

ABCD

A B C D

DCBA

D C B A

A**D

A D

*BC*

Figure 1: Sample data set of normally distributed pseudo-random time series (named as ABCD, DCBA, A**D and *BC*,

illustrated left) with artiﬁcially implanted sinus patterns (labeled as A to D, presented in their occurring order on the right).

ABCD

A**D

*BC*

DCBA

19 19.5 20 20.5 21

ABCD

DCBA

*BC*

A**D

0.005 0.01 0.015 0.02 0.025

Figure 2: Agglomerative hierarchical cluster tree (dendrogram) of synthetic time series data (introduced in Figure 1) according

to the Dynamic Time Warping (left) and our proposed Order-Invariant Distance (right), where the x-axis reveals the distance

between the time series being merged and the y-axis illustrates the corresponding name and shape of the signal.

be classiﬁed in single dots and lines of different di-

rection (Marwan, 2008; Marwan et al., 2007). We are

especially interested in lines that run parallel to the

main diagonal, which occur when the trajectories of

two sub-sequences are similar.

In order to go beyond the visual impressions

yielded by Cross Recurrence Plots, several measures

of complexity which quantify the small-scale struc-

tures have been introduced and are known as Recur-

rence Quantiﬁcation Analysis (RQA) (Marwan, 2008;

Marwan et al., 2007). These measures are based on

the recurrence matrix R(ε) considering a certain ε-

neighborhood. Commonly used measures include re-

currence rate, determinism, entropy as well as average

diagonal line length L:

L(ε,l

min

) =

∑

l=l

min

l · P(ε, l)

∑

l=l

min

P(ε,l)

(5)

where

P(ε,l) =

∑

i, j=1

{(1−R

i−1, j−1

(ε))

· (1− R

i+l, j+l

(ε))

l−1

∏

k=0

i+k, j+k

(ε)}

(6)

is the histogram of diagonal line of length l. The fre-

quency and length of the diagonal lines are obviously

related to a certain similarity between the dynamics of

both time series. A measure based on the lengths of

such lines can be used to ﬁnd non-linear interrelations

between two time series, which cannot be detected

by the common cross-correlation function (Marwan

et al., 2007). To this end, we propose the reciprocal

average diagonal line length of a Cross Recurrence

Plot as an Order-Invariant Distance (OID) measure

for time series that exhibit similar sub-sequences at

arbitrary positions in time.

OID = 1/L (7)

5 CASE STUDY

In this section we demonstrate the practicality of

our proposed Order-Invariant Distance measure on a

sample data set of synthetic time series. As illustrated

in Figure 1, we consider four different normally dis-

tributed pseudo-random time series with artiﬁcially

implanted sinus patterns. The ﬁrst two time series

comprise the same sub-sequences in reverse order,

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

266

ABCD

DCBA

ABCD

A**D

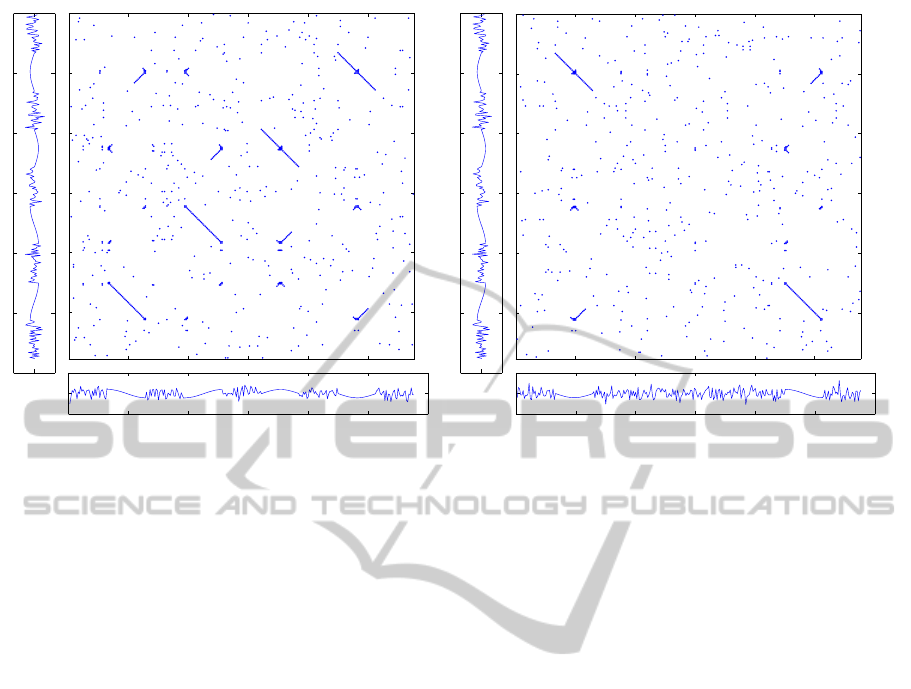
Figure 3: Cross Recurrence Plot (CRP) of synthetic time series ABCD and DCBA (left) as well as ABCD and A**D (right)

introduced in Figure 1. Note that the main diagonal runs from upper left to bottom right.

whereas the last two time series contain a subset of

the artiﬁcially implanted signals.

Figure 2 shows a direct comparison of Dynamic

Time Warping and our introduced Order-Invariant

Distance measure. As expected, the hierarchical clus-

ter tree generated by means of DTW indicates a rela-

tively small distance between the time series ABCD,

A**D and *BC*, because they exhibit similar sub-

sequences at the same positions. However, DTW

treats the time series DCBA as an outlier, due to the

artiﬁcially implanted patterns occurring in reverse or-

der. In contrast, the OID measure considers the time

series ABCD and DCBA as most similar, because the

order of the matched patterns is disregarded. Further-

more, the dendrogram generated by means of OID re-

veals that the time series A**D and *BC* are dissim-

ilar to ABCD and DCBA, which is due to the fact that

the overlap of same or similar sub-sequences is rela-

tively small (≤ 50%).

Figure 3 illustrates the Cross Recurrence Plots of

the time series ABCD and DCBA as well as ABCD

and A**D introduced in Figure 1. Lines parallel to

the main diagonal (from upper left to bottom right) in-

dicate similar sub-sequences in both time series. The

average diagonal line length L is higher for the Cross

Recurrence Plot of the time series ABCD and DCBA

than for the CRP of the pair ABCD and A**D. Since

we want similar time series to have a small distance,

our proposed Order Invariant Distance measure is de-

ﬁned as the reciprocal of the average diagonal line

length (refer to Equation 7).

The presented results serve to demonstrate the ca-

pabilities of the proposed Order-Invariant Distance

measure, rather than to draw any conclusions without

full evaluation. However, we strongly believe that the

introduced OID measure is suitable to determine the

(dis)similarity of time series which exhibit same or

similar sub-sequences at arbitrary positions in time.

6 CONCLUSIONS

In this paper we introduced order invariance for time

series, which has, to our knowledge, been missed by

the community. Hence, we proposed a novel Order

Invariant Distance measure which is able to deter-

mine the (dis)similarity of time series with similar

sub-sequences at arbitrary positions in time.

In addition, we demonstrated the practicality of our

proposed OID measure on a sample data set of syn-

thetic time series with artiﬁcially implanted patterns.

We strongly believe that order invariance is an im-

portant consideration for many real-life data mining

applications. Our future work will include a full eval-

uation on publicly available data.

REFERENCES

Batista, G. and Wang, X. (2011). A complexity-invariant

distance measure for time series. SIAM Internation

Conference on Data Mining (SDM)on Data Mining,

Philadelphia, PA, USA.

Ding, H., Trajcevski, G., Scheuermann, P., Wang, X., and

Keogh, E. (2008). Querying and mining of time series

AnOrder-invariantTimeSeriesDistanceMeasure-PositiononRecentDevelopmentsinTimeSeriesAnalysis

267

data: experimental comparison of representations and

distance measures. Time, 1(2):15421552.

Keogh, E. (2003). Efﬁciently ﬁnding arbitrarily scaled pat-

terns in massive time series databases. volume 2838 of

Lecture Notes in Computer Science, pages 253–265.

Springer Berlin / Heidelberg.

Keogh, E. and Ratanamahatana, C. A. (2005). Exact in-

dexing of dynamic time warping. Knowl. Inf. Syst.,

7(3):358–386.

Lin, J., Keogh, E., and Lonardi, S. (2004). Visualizing

and discovering non-trivial patterns in large time se-

ries databases. In ACM SIGKDD International Con-

ference on Knowledge Discovery and Data Mining,

volume 4, page 61. SAGE Publications.

Marwan, N. (2008). A historical review of recurrence

plots. The European Physical Journal Special Topics,

164(1):3–12.

Marwan, N., Carmenromano, M., Thiel, M., and Kurths, J.

(2007). Recurrence plots for the analysis of complex

systems. Physics Reports, 438(5-6):237–329.

Spiegel, S., Gaebler, J., Lommatzsch, A., De Luca,

E., and Albayrak, S. (2011a). Pattern recognition

and classiﬁcation for multivariate time series. In

KDD-2011: Proceeding of ACM International Work-

shop on Knowledge Discovery from Sensor Data

(SensorKDD-2011), San Diego, CA, USA. ACM.

Spiegel, S., Jain, B.-J., De Luca, E., and Albayrak, S.

(2011b). Pattern recognition in multivariate time se-

ries - dissertation proposal. In CIKM 2011: Proceed-

ings of 4th Workshop for Ph.D. Students in Informa-

tion and Knowledge Management (PIKM 2011), Glas-

gow, UK. ACM.

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

268