
Application of Bio-inspired Algorithm of Structural Optimization to
Automated Design
Mirosław Mrzygłód
Institute of Rail Vehicles, Cracow University of Technology, Al. Jana Pawla II 37, Cracow, Poland
Keywords: Structural Optimization, Bio-inspired Algorithm, Automated Design.
Abstract: The article presents the concept of methodology of automated design based on bio-inspired algorithm of
structural optimization. For the purposes of the automatic design, the constant criterion surface algorithm
(CCSA) is used The algorithm shapes the structure under constant constraint surface rule and gives
possibility to start optimization from a minimum volume arrangement. The automated design schema
considers a minimum effort of the designer that is limited to defining the loads and boundary conditions. To
ensure a high reliability of the automated design process, the CCSA algorithm was enriched by a procedure
of the structure continuity control. As illustrated in the chair example, the application of bio-inspired
algorithm in the automated design framework allows to obtain efficient solution.
1 INTRODUCTION
The high robustness of biological structures and
their mechanism of auto-elimination of weak
solutions can be taken as a direction of research on
the modern design methodology. In order to obtain
the optimum solutions fast it is necessary to
eliminate the restrictions of human mind.
The article presents a concept of methodology of
automated design based on bio-inspired algorithm of
structural optimization. The assumption of such
methodology is to reduce the contribution of the
designer in the designing process only to defining
loads and boundary conditions. For the purposes of
the automatic design, the constant criterion surface
algorithm (CCSA) will be used (Mrzyglod, 2012).
The algorithm belongs to generative evolutionary
design methods (Bentley, 1999) and use indirect
representation similar to the cellular automaton (CA)
algorithm (Tovar et al., 2006). However, the CA
algorithm uses local rules to modify the structure.
The CCSA algorithm is based on the principles
of constant stress surface rule. This idea was first
formulated by Mattheck and Burkhardt (1990) and
states that all biological structures follow the rule of
a constant stress at the surface. Though, the
condition of constant energy density at the free
surface of the optimized structure was first derived
by Wasiutyński (1960).
The CCSA algorithm gives the possibility to do
optimization with various constraints as well as to
solve multi-constraint problems. Moreover, it is also
possible to start the optimization procedure from a
minimum volume layout (unfeasible solution) and
growth structure to its optimum topology. To ensure
high reliability of the automated design process, the
algorithm was enriched by a procedure of the
structure continuity control. The procedure is based
on the intelligent strategy of void identification
(ISOVI) (Mrzyglod, 2011).
2 THE CONSTANT CRITERION
SURFACE ALGORITHM
The optimization problem can be formulated as
follows:
)(min
f
(1)
the constraints are:
jj
gxg
, j = [ 1,2, …, K ]
(2)
where:
= [
1
,
2
,…
N
] is a vector of design
variables defined as
i
i
i
and
are
respectively, intermediate and real material Young’s
modules; g
j
(x) are the criterion parameters;
j
g
are
302
Mrzygłód M..
Application of Bio-inspired Algorithm of Structural Optimization to Automated Design.
DOI: 10.5220/0004157803020305
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 302-305
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
the upper bounds of constraints. The N design
variables represent a pseudo-density (stiffness
parameter) of each finite element of the structures
that vary between
min
and 1. The lower boundary of
pseudo-density
min
is
introduced to prevent
singularity of the equilibrium problem.
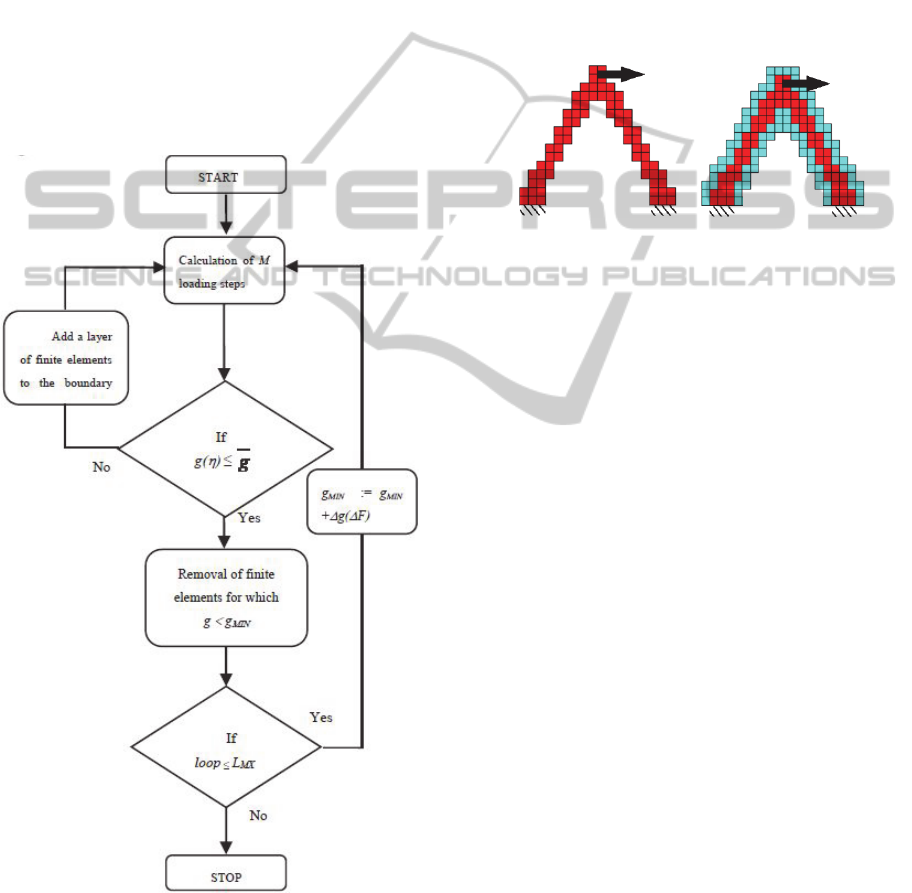
The CSSA algorithm consists of procedure of the
removal and adding procedure of FE elements (see
Fig. 1). The removal procedure of FE elements with
low values of constraint criterion parameters g is
similar to Evolutionary Structural Optimization
(ESO) approach introduced by Xie and Steven
(1993). However, in the CSSA algorithm the volume
value of optimized structure is not assumed a priori
what makes an important difference between those
algorithms.
Figure 1: The constant criterion surface algorithm.
The elimination procedure is controlled by a
F
parameter of volume percentage reduction. To select
the constant value of
F (usually 1%), a constraint
criterion increasing parameter
g at every volume
decreasing iteration is calculated. The FE elements
with values of constraint criterion parameters g
below the g
MIN
limit are eliminated from the
structure. For the volume increasing iteration, there
is no removal operation.
The stress-constrained topology optimization
procedure can give premature results when it is
stuck in point of high values of the state parameter.
In the CCSA algorithm when criterion function
is over the limit, a layer of finite elements is added
to the entire boundary of the structure (see Fig. 1,2).
(a) b)
Figure 2: The layer expansion algorithm: a structure
before (a) and after operation of adding a layer of finite
elements to the structure boundary (b).
The procedure of increasing the volume of the
structure is continued until the criterion parameter g
returns to admissible values. By increasing and
decreasing the structure volume, the algorithm
obtains better solutions after every ‘breakdown’.
This scheme is analogous to the simulated annealing
(SA) (Kirkpatrick et al., 1983).
Furthermore, to ensure reliability of the
optimization process, the continuity control
procedure has been added to the CCSA algorithm. It
prevents the optimization process from being
stopped because of FE solver error. For the
discontinuities detection, the ISOVI procedure based
on automatic pattern recognition is employed
(Mrzyglod, 2011). When the ISOVI procedure
detects a loss of structural continuity, the layer
expansion procedure is turned on. This procedure
will work until the structure returns to the continuity.
This can be treated as self-healing scheme of the
optimization procedure.
The CCSA method to take into account forces
that act in an asynchronous way on the structure, a
‘compare and save maximum’ procedure of
summation of constrain criterion values is proposed
(Mrzyglod, 2010). The procedure assumes, that
during each iteration for every finite element only
the maximum values of the constraint criterion of all
load cases will be written to the equivalent design
space.
ApplicationofBio-inspiredAlgorithmofStructuralOptimizationtoAutomatedDesign
303
The constraint values of final equivalent design
space are used by the constant criterion surface
algorithm of topology optimization.
For multi-constrained topology optimization
problems normalized constraints are introduced
(Mrzyglod, 2012).
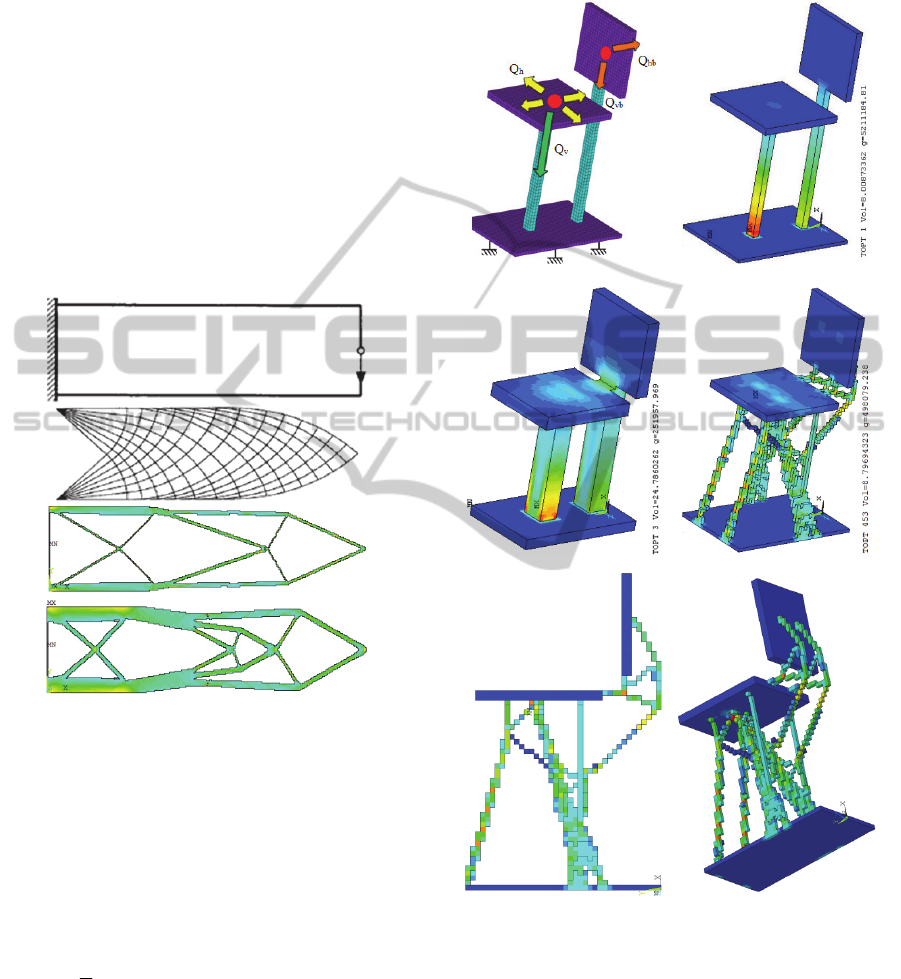
To test the convergence of the algorithm, the
benchmark problem of optimizing truss topology
was selected (Rozvany, 1998) (see Fig. 3a-b). In the
Fig. 3c-d the result of the tests are presented. The
obtained numerical solution is consistent with data
published in the literature for the compliance and
stress constraints (Bendsoe and Sigmund, 2003).
From the example, we can see clear dependency
of final solution on applied load values (see Fig. 3c-
d).
a)
b)
c)
d)
Figure 3: Benchmark problem (Rozvany, 1998): problem
description (a), analytical solution (b), numerical solution
for load Q (c), numerical solution for load 2 x Q (d).
3 EXAMPLE OF AUTOMATED
DESIGN
The chair structure was selected as the example of
automated design. In the example, the mass of the
structure is optimized with the von Mises stress
constraint (
g
= 0.5 MPa,
j = 1
).
The structure is subjected to complex and
asynchronous loading schema: a vertical force Q
v
that is acting on the seat of the chair; horizontal
forces Q
h
= 1/3 Q
v
that are acting in four directions
on the seat; a superposition of forces Q
vb
+ Q
hb
that
are acting on the back of the chair (Q
vb
= Q
hb
= ¼
Q
v
) (see Fig. 4a). The chair FE model with boundary
and results of automated design procedure of the
chair example are presented in Fig. 4a-f. The
history
of searching for a solution is shown
in the Fig. 5.
a) b)
c) d)
e) f)
Figure 4: Example of automated design: FE model with
boundary conditions (a); starting solution (unfeasible)
Vol=8.0% (Vol - percent of volume of the design space N
= 64400) (b); first feasible solution Vol=24.8% (c) best
solution Vol=8.8% (d, e, f).
4 CONCLUSIONS
In the article, the design methodology based on bio-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
304

inspired algorithm is presented. In the algorithm
CCSA, the bio-inspired procedure of shaping the
structure in the form of constant criterion surface has
been joined with local minima avoidance scheme
based on simulated annealing. This ensure achieving
the high efficiency of optimal solution searching.
With the introduction of additional structure
continuity control, the optimization procedure has
been enriched by the possibility of self-repair which
significantly increases the reliability of the
optimization process. As illustrated in the example,
the application of the automated design framework
allowed to obtain efficient solution with minimum
effort of the designer.
Figure 5: Example of automated design: History of
searching for a solution (L
max
= 500).
REFERENCES
Bentley P. J. (Ed.), 1999. Evolutionary design by
computers, Morgan Kaufmann Publishers, San
Francisco, CA.
Bendsoe M. P., Sigmund O., 2003. Topology
Optimization. Theory, Methods, and Applications,
Springer Verlag, New York.
Mattheck C., Burkhardt S., 1990. A new method of
structural shape optimisation based on biological
growth, Int. J. Fatigue, 12(3), 185-190.
Mrzyglod, M., 2010. Two-stage optimization method with
fatigue constraints for thin-walled structures, Journal
of Theoretical and Applied Mechanics, 48(3), 567-
578.
Mrzyglod, M., 2011. A Method of Voids Size
Identification for 2D and 3D Topology. The 2nd
International Conference on Inverse Problems in
Mechanics, IPM2011 ECCOMAS Thematic
Conference, Rzeszow University of Technology, 73–
74.
Mrzyglod M., 2012. Multi-constrained topology
optimization using constant criterion surface
algorithm, Bulletin of the Polish Academy of Sciences
- Technical Sciences, 60(2), 229-236.
Kirkpatrick S., Gelatt C.D., Vecchi M. P., 1983.
Optimization by Simulated Annealing, Science, 220,
671-680.
Rozvany G. I. N., 1998. Exact analytical solutions for
some popular benchmark problems in topology
optimization, Struct Optim 15, 42–48.
Tovar A., Patel N. M., Niebur G. L., Sen M., Renaud J. E.,
2006. Topology Optimization Using a Hybrid Cellular
Automaton Method with Local Control Rules, ASME
Journal of Mechanical Design, 128(6), 1205-1216.
Wasiutyński Z., 1960. On the congruency of the forming
according to the minimum potential energy with that
according to equal strength, Bull. De L’Academie
Polonaise des Sciences, Serie des Sciences
Techniques, 8(6), 259-268.
Xie Y. M., Steven G. P., 1993. A simple evolutionary
procedure for structural optimization, Comput. Struct.,
49, 885-896.
ApplicationofBio-inspiredAlgorithmofStructuralOptimizationtoAutomatedDesign
305
