About Creating Intelligence Systems in Ternary Logic

I. A. Bessmertny, S. V. Eliseev and A. V. Nevidimov

Department of Computer Science, St. Petersburg National Research University of Information Technologies,

Mechanics and Optics (NRU ITMO), Kronverksky pr., 49, Saint Petersburg, 197101, Russian Federation

Keywords: Intelligent Systems, Prolog, Ternary Logic.

Abstract: Rule based intelligent systems traditionally use binary or fuzzy logic. Binary logic by implications causes

contradictions as far as the knowledge base grows, and the bottlenecks of fuzzy logic are

fuzzification/defuzzification processes and computational complexity of inference. A common problem of

all information systems is vulnerability to missing data that can yield wrong results. The paper shows the

opportunity and expediency of creating intelligent systems with the rule-based model of knowledge in

ternary logic basis operating with states “true, false, possible”. Intelligent systems based on ternary logic

allow recognition of a contradiction by the presence in the knowledge base of both the fact and its negation.

Inference from ternary rules not only derives facts by a query but also reveals what facts are missing for the

goal be true. This feature could help to solve the problem of basic level facts that seem to be obvious for a

person but are not presented in the knowledge base. The paper contains examples of Prolog rules for

conversion of binary knowledge bases to ternary ones and some rules for manipulating with ternary facts.

1 PROBLEM DEFINITION

The rule-based model of knowledge is popular and

attractive to use in intelligent systems because of its

similarity to formal logic and natural form of

deduction. Also we know the disadvantages of the

rule-based model grounded on implications that

inevitably cause paradoxes. Attempts to eliminate

the disadvantages of the rule-based model were

made by Lukasiewicz (Łukasiewicz, 1957), Carroll

(Кэролл. 1973), and Brusentsov (Брусенцов, 2008)

who laid down the foundations of ternary logic, that

allows operating not only with “true” and ”false”

values, but also with the third value “unknown”,

”possible”, etc. Some database managements

systems like Oracle (Lex and Gennick, 2005) or MS

SQL Server (Coles, 2007) use NULL field content to

represent missing data in the database and resolve

UNKNOWN for binary operations with NULL

values of variables.

Another method of eliminating the disadvantages

of binary logic is fuzzy logic (soft computing)

suggested by L. Zadeh (Zadeh, 1965), where the

continuous scale between “true” and “false” states is

used. At the same time binary and ternary logics are

particular cases of fuzzy logic. Evident

disadvantages of fuzzy systems are the absence of

standard methods of transition to fuzziness and

backwards (fuzzification and defuzzification) and

computational complexity. Therefore fuzzy logic is

used mainly in expert systems, where cause-effect

relationships are substituted by simple “appearance

– hypothesis” relationships (Бессмертный, 2012). It

should be mentioned that binary logic can be used in

intelligent systems if they get the necessary facts

during the dialogue with the user and this process

solves the paradoxes. Some examples of such

intelligent systems are used by negotiating agents

developed by Xudong et al. (2012), and Minghua et

al., (2006

In intelligent systems with binary logic

elimination of contradictoriness is achieved by

combining the assumptions of closed and open

worlds. But the absolutization of the open world

assumption inevitably leads to most facts become

non-computable. A possible solution is combining of

fuzzy and binary logic as shown by Xudong et al.

(2002).

The objective of the paper is to prove the

usefulness of ternary logic in intelligent systems on

rule based model of knowledge and demonstrate the

implementability of ternary logic in Prolog

programming language.

161

A. Bessmertny I., V. Eliseev S. and V. Nevidimov A..

About Creating Intelligence Systems in Ternary Logic.

DOI: 10.5220/0004109101610165

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 161-165

ISBN: 978-989-8565-30-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 IMPLEMENTATION

Let the knowledge base store the facts in the subject-

predicate-object form. In binary logic, a request to

the fact returns one of two states: true, if the fact

occurs, and false otherwise. False may be returned,

if there exists a fact that explicitly denies the sought-

for fact as well as if there are no data about the fact.

Here is a simple example of this feature of binary

logic.

Let us specify the following query in the subject-

predicate-object form (hereafter we follow the

Prolog notation):

fact(bonnie, hasSex, female).

If the knowledge base contains a relevant fact,

the query returns the “true” value. If there is no

relevant fact in the base, it returns the “false” value

that can be mistakenly interpreted as the fact

«bonnie, hasSex, male».

Let us define three states of fact’s certainty: «1»

– true, «-1» – false and «0» – possible. The truth

table for negation, conjunction and disjunction

operations in ternary basis is written in the table 1.

Table 1: Truth table.



X ∧ 

X∨

-1 1 -1 -1 -1 -1

0 0 -1 0 -1 0

1 -1 -1 1 -1 1

0 0 0 0

0 1 0 1

1 1 1 1

The rules of transforming binary facts to ternary

ones are listed below:

∃fact → ternar



fact,1



(1)

∃φ,φ → fact



 → ternaryfact,‐1

(2)

∃



fact,∃



φ,φ→fact



→ternaryfact,0

(3)

The first rule (1) ascertains the fact’s Certainty

(Certainty=1) if the corresponding binary fact is

presented. The rule can be written in Prolog as

shown below.

ternary(Subj,Pred,Obj,1):-

fact(Subj,Pred,Obj).

Beyond the triple arguments (subject, predicate,

object), each ternary fact should have the fourth

argument certainty.

The second rule (2) establishes the falseness of

the fact (Certainty = -1) for a subject having

mutually exclusive states. This rule is context-

sensitive and should be set individually for each fact.

For the example described above negative fact looks

ternary(Subj,hasSex,male,-1) :-

fact(Subj,hasSex,female).

The third rule (3) defines the fact is possible

(Certainty=0) if there are no confirming nor negating

facts:

ternary(Subj,Pred,Obj,0,

[Subj,Pred,Obj]):-

not(fact(Subj,Pred,Obj)),

not(ternary(Subj,Pred,Obj,-1)).

Contrary to (2), rules (1) and (3) are universal

and could be applied to all the facts of a binary

knowledge base. Rule (3) uses as antecedents non-

existing facts, consequently, it can yield a ternary

fact only by back chaining reasoning, i.e. by query

processing.

Presence of the ternary facts with both “1” and ”-

1” certainties for the same binary fact in the

knowledge base is a symptom of its inconsistency

and this can be used for its verification.

In contrary to reasoning from binary facts by

Prolog inference engine, when failure occurs if there

are no facts satisfying the query or a condition of the

rule, reasoning by Prolog from ternary knowledge

base never yields failure because any ternary fact is

presented in a knowledge base (with certainty +1, 0

or -1). Consequently, Prolog will always return

truth, so the certainty of the result is to be calculated

as the minimum certainty of all the conditions of the

rule as shown below:

ternary(X,oppositeSex,Y,Cty) :-

ternary(X, hasSex, male, Cty1),

Cty1>=0,

ternary(Y,hasSex,female,Cty2),

Cty2>=0,

Cty is min(Cty1,Cty2).

ternary(X,oppositeSex,Y,Cty):-

ternary(Y,oppositeSex,X,Cty).

This rule returns certainty of the result: Cty = 1

(the “true” value), if X and Y are of different sexes;

Cty = -1 (the “false” value), if X and Y are asexual

or neutral; or Cty = 0 (the “possible” value), if the

sexes of X and Y are unknown. In this example two

instances of the rule mean that getting the result

requires applying disjunction to each rule.

According to the truth table (Table 1) disjunction in

ternary logic means the maximum of certainties of

operands, so it is always necessary to find all the

solutions and choose one with maximum value of

certainty. Let us write the goal:

ternary(bonnie,oppositeSex,clyde,Cty).

If the knowledge base contains just the fact

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

162

fact(bonnie, hasSex, female),

the first rule obviously returns the certainty Cty = -1

(bonnie has no sex male) and the second one gives 0

(bonnie has sex female but sex of clyde is

unknown). Thus, the resulting Cty = 0.

3 INFERENCE EXPLAINING

AND VISUALIZATION

Involvement of more than one fact in a rule that

returns “0” significantly reduces information

capacity and usefulness of the result, because we do

not know which fact impedes the revealing of the

truth of the result. For ascertainment of such missing

facts the list of the facts with zero truth value could

be returned in this form of a list:

ruleconsequent,

fact1,…,factN

(4)

Such a list can be interpreted as a phrase in a

subjunctive mood: “This fact can be true, if the

following facts are true …”. In contrast to expert

systems where the missing facts are to be established

in a human-machine dialogue we need not to involve

the user to the consideration process. The resulting

lists of uncertain facts can be analyzed

automatically.

The following is the modified rule which defines

that a subject and an object are of the opposite sex:

ternary(X,oppositeSex,Y,Cty,

[X,oppositeSex,Y,Cond1,Cond2]) :-

ternary(X,hasSex,male,Cty1,Cond1),

Cty1>=0,

ternary(Y,hasSex,female,Cty2,Cond2),

Cty2>=0,

Cty is min(Cty1,Cty2).

ternary(X,oppositeSex,Y,Cty,Cond):-

ternary(Y,oppositeSex,X,Cty,Cond).

The fifth argument in the ternary predicate

contains the list of facts needed to the fact be true.

This argument has the empty list in facts with

certainty values 1 and -1.

Below is one more rule that defines the

allowability of marriage based on conditions that the

partners have opposite sex:

ternary(X,canMarry,Y,Cty,

[X,canMarry,Y,Cty,Cond):-

ternary(X,oppositeSex,Y,Cty,Cond),

Cty>=0.

Let us issue the Prolog goal:

ternary(bonnie,canMarry,clyde,

Cty,Explanation).

If the knowledge base contains fact(clyde,

hasSex, male) but no fact(bonnie, hasSex, female),

certainty Cty = 0 and the reason is following:

[bonnie,canMarry,clyde,

[bonnie,oppositeSex,clyde,

[bonnie,hasSex,female]]].

Now we can consider the peculiarities of

negation operation. To include the rule with

negation into an antecedent, the certainty of this

condition should be inverted:

ternary(X,canMarry,Y,Cty,[X,canMarry,

Y,Cty,Cond1,[‘NOT’|Cond2]):-

ternary(X,oppositeSex,Y,Cty1,Cond1),

Cty1>=0,

ternary(X,bloodRelative,Y,Cty2,

Cond2), Cty2=<0,

Cty is min(Cty1,-Cty2).

The above example of modified rule forbids the

marriage of blood relatives and the reason acquired

after query processing is following:

[bonnie,canMarry,clyde,

[[bonnie,oppositeSex,clyde,

[bonnie,hasSex,female],

[NOT,bonnie,bloodRelative,clyde]].

By using nested rules and large number of facts

the inference chains can be very long so the lists of

uncertain facts get unreadable for a man. At the

same time the list structure of data is convenient for

interpreting by computer. Another problem of

explaining of inference results is layerage of

negations that can also make the explaining difficult.

These problems could be solved by visualization of

uncertain facts by semantic graphs like it was shown

for knowledge visualization (Bessmertny, 2010).

Fig. 1 demonstrates the visualization of uncertain

facts needed for the inference “Bonnie can marry

Clyde” to be true.

Figure 1: Visualization of uncertain facts for the inference

“Bonnie can marry Clyde”.

NOT

bonnie,canMarry,clyde



bonnie,oppositeSex,clyde

bonnie,

bloodRelative,clyde

bonnie,hasSex,female



AboutCreatingIntelligenceSystemsinTernaryLogic

163

The proposed method of creating rules allows

eliminating the disadvantages of intelligent systems

with the rule-based model of knowledge caused by

binary logic and also provides solutions that are not

just the statements of facts. Modelling of reasoning

with explaining how the goal can be achieved makes

intelligent informational systems closer to expert

systems in terms of the explanation of the results and

allows simplify the verification of knowledge bases.

4 DISADVANTAGES AND

CONSTRAINTS

In intelligent systems with large quantities of facts

and rules a great number of response instances that

differ in fact combinations can be expected for each

positive result of the query. The interpretation of

response categories also may be a rather difficult

task. For example, the knowledge base contains no

data about instances Alex and Cruz. Then the query

ternary(alex,canMarry,cruz)

yields two lists of uncertain facts:

[alex, canMarry, cruz, [[alex,

oppositeSex, cruz, [[alex, hasSex,

male], [cruz, hasSex, female]]], [NOT,

alex, bloodRelative, cruz]]];

[alex, canMarry, cruz, [[alex,

oppositeSex, cruz, [[alex, hasSex,

female], [cruz, hasSex, male]]], [NOT,

alex, bloodRelative, cruz]]].

Of course, more complex rules will generate

many lists and interpretation of them might be a

non-trivial task. The simplest decision here is sorting

the lists by their length by ascending. Another way

is intersection of lists to detect common conditions.

If these conditions are unachievable the entire goal

is unreachable.

The second disadvantage is that the number of

facts involved in conjunction and disjunction is not

considered in ternary logic whereas in fuzzy logic

conjunction and disjunction can be substituted not

by minimum and maximum but by Bayes' formulas

or random relations. This problem can be solved

partially if all the solutions are sorted by the length

of the list of conditions and the solution with the

minimal quantity of undetermined facts is chosen. It

should be admitted that fuzzy logic also meets

computational problems as shown by Xudong

(1997).

5 PERFORMANCE ANALYSIS

Complexity of inference in binary logic by depth-

first method is b

nodes, where b is branching

coefficient and m is search depth (Russel and

Norwig. 2010). For the binary facts the branching

coefficient b means the average number of fact

combinations relevant to the rule conditions. The

branching coefficient for ternary knowledge base is

higher because the missing and negative facts are

always presented with certainty 0 and -1

respectively. Consequently, the search in ternary

knowledge bases is more complicated., The search

depth in ternary logic is not expected to be deeper so

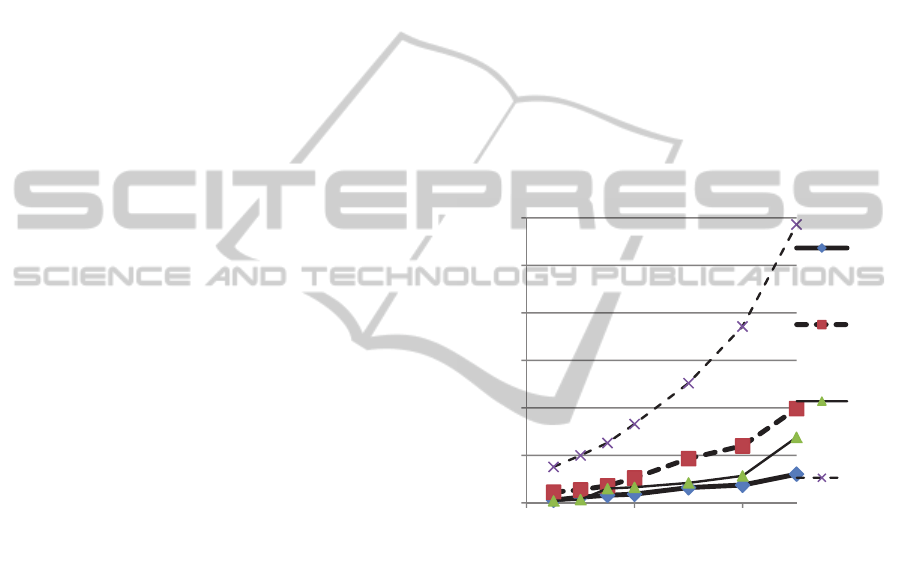
the complexity growth will be not significant. Fig.2

presents the results of experimental research of

knowledge acquisition from the base of facts

containing predicates “has_child” and “has_sex”.

Figure 2: Time of acquisition 100000 facts.

All the instances of subjects and objects are

random numbers, where gender attribute was

defined only for 75% of instances. For the search

depth m=1 the rule “oppositeSex” and for m=2 the

rule “canMarry” were applied. The curves (1) and

(2) correspond to the search the facts “oppositeSex”

and the curves (3) and (4) show the search the facts

“canMarry” in binary and ternary logic respectively.

The results of experiments in the SWI-Prolog

environment demonstrates approximately 3 – 5

times less speed of inference in ternary logic and

these results meet the expectations.

6 CONCLUSIONS

The presented results of research demonstrate the

100

150

200

250

300

0 20000 40000

Time, s

Number of facts in the knowledge base

(1)

(2)

(3)

(4)

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

164

efficiency of the principles of creating intelligent

systems in ternary logic basis. At the same time

there is no necessity to use the open world

assumption, and an intelligent system gets a totally

new quality: neither the truth nor the falseness of

any fact is defined but the possibility of its truth

mentioning the conditions under which the truth of

the fact can be achieved. The problem of the speed

of modeling the deductions in ternary logic is not

discussed in the research. It is likely that the

methods of inference acceleration developed by the

authors and represented in the papers

(Бессмертный, 2012), (Bessmertny and

Katerinenko, 2011) could be used for this purpose

and are to be an objective for further work

REFERENCES

Coles, M. (2007) "Null Versus Null?". SQL Server Central

(Red Gate Software), February 26.

Lex de Haan and Gennick, J. (2005) "Nulls: Nothing to

Worry About". Oracle Magazine, July–August.

Łukasiewicz, J. (1957) Aristotle’s Syllogistic from the

Standpoint of Modern Formal Logic. Oxford

University Press. 2nd Edition, enlarged. Reprinted by

Garland Publishing in 1987. ISBN 0-8240-6924-2.

Bessmertny, I. (2010) Knowledge Visualization Based on

Semantic Networks. Programming and Computer

Software. - M: Pleiades Publishing, Ltd. Distributed

Worldwide by Springer. - Vol. 36. - N 4. - P. 197-204.

- ISSN 0361-7688.

Bessmertny I., Katerinenko R. (2011) Inference

Acceleration in Production Model of Knowledge.

Programming and Computer Software. - Vol. 42. –

No. 4. - P. 197-199. - ISSN 0361-7688.

Russell, S. and Norvig, P. (2010) Artificial Intelligence: A

Modern Approach. Third Edition. – Prentice Hall.

Xudong, L., Chunyan, M, Jennings, N., Minghua, H.,

Zhiqi, S., Minjie, Z. (2012) Kemnad: a Knowledge

Engineering Methodology for Negotiating Agent

Development. Computational Intelligence 28(1): 51-

105. http://eprints.soton.ac.uk/ 271758/1/Luo_CIpap-

er_fanal011210.pdf.

Minghua, H., Rogers, A., Xudong, L., Jennings, N. (2006)

Designing a successful trading agent for supply chain

management. AAMAS: 1159-1166 http://eprints.so-

ton.ac.uk/ 261967/ 1/TACSCM9.pdf.

Xudong, L., Chengqi, Z., Jennings, N. (2002) A Hybrid

Model for Sharing Information Between Fuzzy,

Uncertain and Default Reasoning Models in Multi-

agent Systems. International Journal of Uncertainty,

Fuzziness and Knowledge-Based Systems. No 10(4):

p. 401 - http://eprints.soton.ac.uk/ 256876/1/

jufkbs.pdf.

Xudong, L., Chengqi, Z., Jingqiu, C. (1997) The

Weighting Issue in Fuzzy Logic. Informatica: An

International Journal of Computing and Informatica,

No. 21(2), pp. 255-262.

Zadeh, L. (1965) “Fuzzy Sets”. Information and Control,

No. 8, pp.338-353.

Бессмертный, И. (2012) Интеллектуальные системы

на продукционной модели знаний: Проблемы

практической реализации.: LAP LAMBERT

Academic Publishing GmbH & Co. KG, ISBN 978-3-

8473-4142-0.

Брусенцов, Н. (2008) Исчерпывающее решение

«неодолимой» проблемы парадоксов. М.: Фонд

"Новое тысячеление".

Кэролл, Л. (1973) Символическая логика. М.: Мир.

AboutCreatingIntelligenceSystemsinTernaryLogic

165