Modelling How Students Organize Knowledge

Ismo T. Koponen

Department of Physics, University of Helsinki, Helsinki, Finland

Keywords:

Knowledge Organization Patterns, Concept Maps, Directed Networks, Learning.

Abstract:

We discuss here how students organize their knowledge (in physics) by connecting closely related concepts.

Attention is paid on the relational structure of the ordering of concepts so that the introduction of new concepts

is justiﬁed on the basis of concepts which have already been learned. Consequently, there is then direction of

progress in introducing new concepts - there is ”ﬂux of information” so that what was learned before is the

basis for learning new conceptual knowledge. Such ordered and directed process of introducing the concepts

can be conveniently described and analysed in the framework of directed ordered graphs. We propose here a

model of knowledge organization for such concept maps. The model is based on the assumption that students

use simple procedures connecting new concepts mostly to concepts introduced few steps before. On basis of

the model results we suggest that the most important properties of concept maps can be understood on a basis

of such simple rules for organising knowledge.

1 INTRODUCTION

Scientiﬁc knowledge is quite often described as webs

or networks, where concepts are linked to other con-

cepts and principles; concepts are thus conceived as

parts of the whole system of knowledge. In such a

picture of knowledge, it is evident that the existing

structure and relations within it also affect how the

new concepts can be introduced (as parts of the net-

works) and how the conceptual knowledgecan be rep-

resented and transferred forward (Thagard, 1992; No-

vak, 2002; O’Donnell et al., 2002). Consequently,

knowledge processing and acquisition have been re-

cently discussed within the framework of network

theory (Costa, 2006; Batista and Costa, 2010; Goni

et al., 2010). Such an approach seems to be well

adapted also in describing knowledge processing in

learning, in particular how students organize their

conceptual knowledge and, on the other hand, how

conceptual knowledge can be approached in learning

and teaching (Koponen and Pehkonen, 2010; Kopo-

nen and Nousiainen, 2012).

In teaching and learning the network of concepts

is often represented by using concept maps (McClure

et al., 1999; Novak, 2002; O’Donnell et al., 2002;

Koponen and Pehkonen, 2010). Here we focus on

the question, can we possibly understand the local

and global structure of concept maps by making as-

sumptions about the rules or strategies students may

have used in construction of the maps. The empiri-

cal sample discussed here consists of concept maps

made by physics teacher students for purposes of or-

ganising content knowledge for teaching. The linking

of concepts is done by paying attention on how con-

cepts are used in quantitative experiments and con-

struction of models. As we have shown previously

(Koponen and Nousiainen, 2012), such students con-

cept maps representing their knowledge of (or about)

physics concepts can be analysed conveniently and re-

liably within the theoretical framework based on di-

rected ordered graphs (Karrer and Newman, 2009;

Goni et al., 2010). Here we develop a phenomeno-

logical model for knowledge ordering based on di-

rected ordered graphs (DOGs). We show that the typ-

ical structural features of students’ concept maps can

be modelled by assuming that concepts are mostly re-

lated to nearby concepts one or two concepts away,

with few links between concepts about 10-15 steps

away. When concepts are introduced in this way in

ordered succession, substantial number of triangular

patterns (as found in the real networks) are quite nat-

urally generated. Comparison of the model results

with the real student concept maps shows that the

model reproduces the salient properties of connected-

ness and ordering found on students’ concept maps.

Consequently, the results suggest that students indeed

use simple but effectivestrategies in ordering and pro-

cessing their knowledge.

143

Koponen I..

Modelling How Students Organize Knowledge.

DOI: 10.5220/0004105201430148

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 143-148

ISBN: 978-989-8565-30-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 CONCEPT NETWORKS

The relational structure of concepts can be thought

as network-like node-link-node representations of the

relations between concepts. For different types of rep-

resentations there are different ways of establishing

the relations and different rules in regard to linking

the concepts, but the skeletal structure of the concept

network is always a network of nodes (i.e. concepts)

connected by links. The concept networks studied

here are done by physics teacher students for purposes

of representing how they think concepts can be intro-

duced in teaching, so that each step is justiﬁed either

on basis of experiments or model, which are both cen-

tral procedures connected to the construction and use

of knowledge. It is then natural to assume that these

procedures of the experiments and modelling play an

important role in conferring the structure of the con-

cept networks. In the operationalizing experiment

the concept is operationalized i.e. made measurable

through the pre-existing concepts. The new concept

or law is constructed sequentially, starting from the al-

ready existing ones, which provide the basis for an ex-

periment’s design and interpretation. In its most ide-

alized form the new concept (or law) C is formed on

the basis of two pre-existing concepts A and B so that

the operationalization creates C on the basis of the re-

lations A → C and B → C, but which also requires

that A and B can be related as A → B. There is then

a triangular mutual dependence A → B → C ← A.The

modelling procedures, which in the simplest cases are

often deductive procedures, produce very similar pat-

terns (Koponen and Pehkonen, 2010; Koponen and

Nousiainen, 2012). It is interesting to note cognitively

oriented studies of knowledge formation suggest that

procedures of knowledge construction and processing

may be simple ones, reducible to basic patterns, even

in those cases where the resulting structures are com-

plex. In that,triangular patterns have been recognized

as an essential feature not only in the case of func-

tional knowledge but also in information acquisition

as well as information processing (Kemp et al., 2007;

Kemp and Tenenbaum, 2008; Duong et al., 2009).

The procedures of constructing experiments and

models – connecting concepts to previously intro-

duced concepts – then provide the context or the “af-

ﬁliations” of concepts. Concept maps where these

procedures are used to connect concepts represent

then not only the relatedness of concepts, but they

also represent how concepts are introduced in teach-

ing so that knowledge learned earlier is the basis upon

which new knowledge is built. This means that, in a

sense, these networks also represent the ”ﬂux of in-

formation” which students have planned to take place

in their teaching. In well-planned teaching there

should naturally be a regular ﬂux of information (for

evenly paced learning of new knowledge), but no

unnecessary abrupt changes in that ﬂux (otherwise

the demand to assimilate new knowledge would vary

much); moreover, uncontrollable reductions in the

ﬂow should be hindered to prevent the impression that

learned knowledge would not be needed in further

learning (Koponen and Nousiainen, 2012).

3 THE METHOD OF ANALYSIS

The properties of ordering and information ﬂux in

the concept maps are explored by using the quantities

based on theory of directed ordered networks (DOGs)

(Karrer and Newman, 2009; Goni et al., 2010). Be-

cause we are interested in the connectedness and in-

formation ﬂuxes in the maps, we use the follow-

ing quantities (detailed mathematical deﬁnitions are

given in Table 1):

1. The degree k

of the node, which is the number

of the incoming and outgoing links k

and k

out

respectively. The average degree is denoted by D;

2. The clustering coefﬁcient C

, which is the ratio

of triangles to all the triply connected neighbours

around a given concept;

3. Flux into the nodes (Flux-I) Φ

, which gives the

total number of links terminating at the givennode

k from all levels j < k;

4. Flux around the nodes (Flux-A) Ψ

, which gives

the total number of links bypassing the given node

k from all levels j < k.

In the present case, ﬂuxes Φ and Ψ directly describe

the ”information” ﬂowing from the previously in-

troduced nodes to ones introduced later (Karrer and

Newman, 2009). The most important aspect of the

concept maps made by teacher students is their or-

dering and appreciably large clustering with C ≈ 0.2.

Both features follow from the procedures that are used

to connect concepts. It is of interest to develop a sim-

ple model, which captures these features. In addition

to these features the model should also reproduce the

steady node-by-node information ﬂows Ψ and Φ.

4 THE MODEL

The cases studied and modelled here consist of 8 stu-

dent maps, all of which are rather rich in their struc-

ture. The number of the concepts was limited to n=34

most central concepts (in electromagnetism). Details

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

144

Table 1: Deﬁnitions of the quantities characterizing the

topology of the concept networks. In the deﬁnitions a

the element of the adjacency matrix a and N is the number

of nodes. The quantities are deﬁned for a given node i. The

average number of links k

per node is denoted by D.

Quantity Deﬁnition

∑

out

∑

+ k

out

∑

′

> j

˜a

j j

′

˜a

′

∑

′

> j

˜a

′



∑

i−1

j=1

out

−

∑

i−1

j=1





∑

i−1

j=1

out

−

∑

j=1



Figure 1: An example of students’ concept maps (Gs) for

n = 34 concepts in electromagnetism. The map shows con-

cepts (boxes), laws and principles (boxes with thick bor-

ders). Links are either operationalising experiments (E) or

modelling procedures. The nodes are numbered in the order

in which they are introduced through experiments.

of the maps are not of interest here and are discussed

in detail elsewhere (Koponen and Nousiainen, 2012).

An example of the original concept maps made by

students is shown in Fig.1

For purposes of comparison and reference, we

have also constructed a ”master map”, where all

well-motivated and well-justiﬁed connections that are

found in the student maps are collated into one map.

For purposes of analysis it is convenient to use for

all maps the so called ”spring-embedding”(Kolaczyk,

2009), which brings about the most important nodes

as clusters of links. Examples of spring-embedded

maps (one student map and the master map) are

shown in Fig. 2.

Basic assumptions we have made about how the

learners process and represent knowledge are as fol-

Figure 2: The ”master map” (Gm) and one students’ map

(G1) in spring-embedded form.

lows: 1) New concepts are introduced on basis of

old ones so that relatively few (from two to four) of

them are used as basis of introducing the new ones;

2) The procedures provide the context or the “afﬁli-

ation” for making the connections. 3) Concepts are

recognized on basis of the phenomenological mean-

ing. This gives rise to the modularity.

On the basis of above notions 1-3 we suggest a

model, where nodes 1,2,. . . i − 1, i, i + 1,...n are in-

troduced sequentially so that each node i + 1 is con-

nected in directed way to some of the preceding nodes

1,2,.. . i. The directionality is deﬁned from ances-

tor nodes to new nodes. The probability distribu-

tion function (PDF) that i + 1 connects to the given

ancestor i

′

which is j steps away from it i.e. to

node i

′

= i + 1 − j is assumed to follow a gamma-

distribution

i, j

(α,λ) =

(α,λ)

α−1

exp[−λj] , (1)

where parameters α and λ control the form of the dis-

tribution. The normalization Z

(α,λ) is obtained in

closed form in terms of the Lerch’ transcendental Phi-

function φ

κ,i

(z) ≡ φ(z,κ, i)

(α,λ) = φ

1−α,1

−λ

)−e

−λ(α−1)

1−α,1+i

−λ

) (2)

In practice, the detailed functional form of the dis-

tribution is not crucial, given it is peaked. Gamma-

distribution is chosen because it is ﬂexible and the cu-

mulative distribution function (CDF) for PDF in Eq.

(1) can be given in form

F(i, j) =

∑

′

i, j

′

(α,λ)

(3)

The nodes are connected on basis of CDF in Eq. (3)

by using event based Monte-Carlo method. First, the

number N of connection attempts is selected, then for

each attempt a random number r ∈ [0, 1] is generated

and the new node is connected to ancestor node at

a distance j

∗

, obtained from r = F(i, j

∗

) by inver-

sion. In practice, values of j

∗

corresponding differ-

ent r are tabulated in advance for each i, so that the

ModellingHowStudentsOrganizeKnowledge

145

Table 2: Simulation parameters for models m-G1, m-G2

and m-G3. Subscripts A an B refer to values for modules A

and B separately, subscript AB to values between modules

A and B.

m-G1 2 2/3 2 2/3 2 1/3

m-G2 5/2 2/5 5/2 2/5 7 1/3

m-G3 2 2/5 2 2/5 5 1/3

repeated inversion of r = F(i, j

∗

) during the simula-

tion is avoided. When connection attempt is repeated

N times same attempts to connect already connected

nodes may occur, in which case no multiple connec-

tions are allowed.

In the simulation model we have two modules A

and B (corresponding two modules in maps, for two

topical areas) and within the both modules we use the

same above explained method to connect the nodes,

but the values of the parameters α, λ, and N can be

different for modules A and B. Connection between

the nodes in different modules is also made on same

basis. The parameters for models are given in Table 2.

The networks based on these simulations are visually

very similar to students’ networks. Examples to be

compared with student networks are shown in Fig. 3.

Figure 3: The model graphs m-G1 and m-G2 in spring-

embedded form.

The analysis of the networks is carried out on basis

of their adjacency matrices a, where the variables a

indicate the connections between nodes i and j so that

if nodes are connected, then a

= 1 and if there is

no connection, then a

= 0. All quantities of interest

can now be calculated from the matrix a as they are

deﬁned in Table 1.

5 RESULTS

The student maps have relatively high clustering and

connectedness (Koponen and Nousiainen, 2012). On

average the clustering attains values around 0.10-

0.25, which is common to networks designed for pur-

poses of passage of information (Kolaczyk, 2009).

Large values of clustering indicate that there are ap-

preciable connections also between concepts con-

nected to a given concept, i.e. an abundance of the

nearest neighbour connections. High connectivity (on

average 3-4 links per node) means that the informa-

tion ﬂuxes are also rather large. The ﬂuxes are given

as a total ﬂux per expected number of links (total ﬂux

divided by average value D of links per node, see

Table 1 for deﬁnition. The results reveal that typi-

cally, per one link connected to a given node, there

are from three to four links coming from the lower

levels. This means that each node is rather well sup-

ported by the many previous nodes - the meaning con-

tent of the concept (node) is supported or backed up

by knowledge contained on the network existing be-

fore the introduction of the new node. In general, just

these properties must be reproduced by model which

attempts to capture the essential features of the maps.

Running the simulation for different choices of pa-

rameters shows that there is a range of parameters,

where it is possible to obtain networks very similar

to the empirical ones. It should be noted that it is

not of interest (or even possible) to try to optimize

parameters so that for a given empirical network ex-

actly similar network is found in simulations. Instead,

Simulations are used to explore the ensemble of pos-

sible networks and how the measurable properties of

the networks are distributed within these ensembles

and how the values of degree D, clustering C, and

ﬂuxes Φ and Ψ compare with the empirical obser-

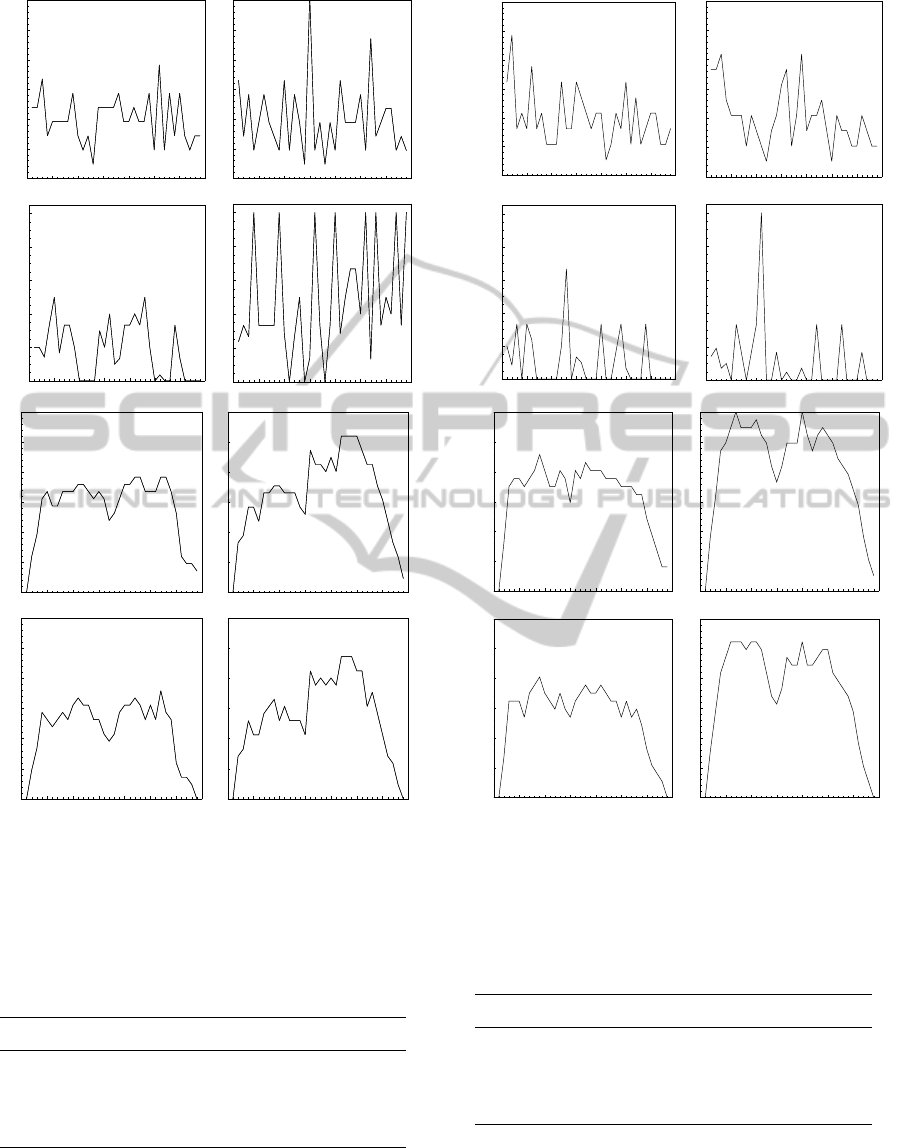
vations, as is shown by results in Figs. 4 (empirical

results) and 5 (model results). The average values of

the clustering and ﬂuxes are given in Table 3 for some

of the students’ maps and model maps. For compari-

son, some other values of students’ maps are given in

Table 4. From the results it seen that the model repro-

duces the most important qualitative features of the

maps and, in addition, quantitative agreement is sat-

isfactory taken into account the variation of measured

values within the student maps (see Table 4).

6 CONCLUSIONS

The relational structure of concepts in the concept

networks made by physics teacher students have re-

vealed that properties of such networks are domi-

nated by triangular knowledge organisation patterns

so that the structure has thus relatively high clustering

of nodes but yet performs well in passing the informa-

tion i.e. information ﬂuxes provided the connections

are high (Koponen and Nousiainen, 2012). It is

assumed that these properties can be traced back to

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

146

Gm, D=4.18

0.0

0.5

1.0

1.5

2.0

2.5

3.0

Number of links kD

èèèè

Gs, D=4.24

0.0

0.5

1.0

1.5

2.0

2.5

3.0

0.0

0.2

0.4

0.6

0.8

1.0

Clustering C

0.0

0.2

0.4

0.6

0.8

1.0

Flux-I  D F

Node

Flux-A  D Y

Node

Figure 4: Node-by-node (nodes 1-34) values of degree D,

clustering C, and ﬂuxes Φ and Ψ. The ﬁrst column shows

the values for master map Gm and the second column for

the student map G1.

Table 3: Average degree D, clustering C and information

ﬂuxes Ψ and Φ for master map Gm and student maps G1

and G2 and for models maps m-G1 - m-G3.

Gm G1 G2 m-G1 m-G2 m-G3

D 4.18 3.47 4.24 3.71 4.47 3.58

C 0.18 0.25 0.48 0.19 0.33 0.24

Φ 2.82 3.00 3.31 2.73 3.20 3.09

Ψ 2.32 2.51 2.81 3.06 2.81 3.01

students’ systematic use of simple procedures (here

quantitative experiments and modelling) which they

use to add new concepts on the existing concept net-

work.

m-G1, D=3.71

0.0

0.5

1.0

1.5

2.0

2.5

3.0

Scaled degree kD

m-G2, D=3.82

0.0

0.5

1.0

1.5

2.0

2.5

3.0

0.0

0.2

0.4

0.6

0.8

1.0

Clustering C

0.0

0.2

0.4

0.6

0.8

1.0

Flux-I  D F

èè

Node

Flux-A  D Y

Node

Figure 5: Node-by-node (nodes 1-34) values of degree D,

clustering C, and ﬂuxes Φ and Ψ. The ﬁrst column shows

the values for model graph m-G1 and the second column for

the graph m-G2.

Table 4: Average degree D, clustering C and information

ﬂuxes Ψ and Φ for six student maps G3-G8.

G3 G4 G5 G6 G7 G8

D 2.85 3.06 3.18 3.18 3.72 4.07

C 0.24 0.15 0.25 0.16 0.21 0.17

Φ 1.84 2.76 2.97 3.12 3.19 2.70

Ψ 1.34 2.26 2.47 2.65 2.62 2.21

In order to conﬁrm these expectation, a simple

phenomenological model simulating the process of

making the connections was introduced. In the model,

there are two assumed modules of concepts. Within

the module closely located nodes have higher prob-

ModellingHowStudentsOrganizeKnowledge

147

ability to connect, but there is appreciably smaller

probability for connection between the modules (on

the average 15-20 % of connections between mod-

ules). These simple rules seem enough to generate

networks with very similar properties as those found

empirically.

The conclusion we can draw from the results with

some conﬁdence is that learners handle the knowl-

edge so that they process the relational aspect in rather

small pieces, ﬁnding the connections on basis of “af-

ﬁliation” of concepts in the procedures (experiments

and models), where they are used. In the context stud-

ied here - making plans for teaching - this is natu-

ral and desired aspect. In more general (and spec-

ulative level) the results support the assumption that

processing of knowledge is based on simple afﬁli-

ation schemes. In certain context of description or

prediction few known concepts are used, and new

concept (knowledge) or new generalization is intro-

duced on basis of the already known concepts (knowl-

edge). The fact that in each context (afﬁliation) only

few known concepts is used tells probably something

about the: 1) human capability to process and handle

knowledge, 2) human capability to infer dependen-

cies. In short, there seems to be preference for certain

parsimony in handling the knowledge. Of course, this

ﬁnding is not very unexpected, but nicely conﬁrmed

here through structural analysis of knowledge rep-

resentations. These notions encourage thinking that

the methods developed here provide a fruitful start-

ing point for monitoring learning outcomes and can

give insight to the ways knowledge is processed and

represented.

ACKNOWLEDGEMENTS

This work has been supported by the Academy of Fin-

land through grant SA133369.

REFERENCES

Batista J. B. and Costa, L. da F. (2010). Knowledge Acqui-

sition by Networks of Interacting Agents in the Pres-

ence of Observation Errors. Physical Review E, 82,

016103.

Costa, L. da F. (2006). Learning About Knowledge: A

Complex Network Approach. Physical Review E, 74,

026103.

Duong, T. H., Jo, G. S., Jung, J. J. and Nguyen, N. T.

(2009). Complexity Analysis of Ontology Integra-

tion Methodologies: A Comparative Study. Journal

of Universal Computer Science, 15, 877–897.

Goni, J., Corominas-Murtra, B., Sol´e, R. V. and Rodr´ıguez-

Caso,C. (2010). Exploring the Randomness of Di-

rected Acyclic Networks. Physical Review E, 82,

066115.

Karrer, B. and Newman, M. E. J. (2009). Random Graph

Models for Directed Acyclic Networks. Physical Re-

view E, 80, 046110.

Kemp, C., Perfors, A. and Tenenbaum, J. B. (2007). Learn-

ing Overhypotheses with Hierarchical Bayesian Mod-

els. Developmental Science, 10, 307-321.

Kemp, C. and Tenenbaum, J. B. (2008). The Discovery of

Structural Form. PNAS, 105, 10687–10692.

Kolaczyk, E. D. (2009). Statistical Analysis of Network

Data. New York: Springer.

Koponen, I. T. and Pehkonen M. (2010). Coherent Knowl-

edge Structures of Physics Represented as Concept

Networks in Teacher Education. Science & Educa-

tion, 19, 259–282.

Koponen, I. T. and Nousiainen M. (2012). Pre-service

physics teachers understanding of the relational struc-

ture of physics concepts. International Journal of

Science and Mathematics Education, in print, DOI

10.1007/s10763-012-9337-0.

McClure, J. R., Sonak, B. and Suen, H. K. (1999) Concept

Map Assesment of Classroom Learning: Reliability,

Validity, and Logistical Practicality. Journal of Re-

search in Science Teaching, 36, 475–492.

Novak, J. (2002). Meaningful Learning: The Essential Fac-

tor for Conceptual Change in Limited or Inappropriate

Propositional Hierarchies Leading to Empowerment

of Learners. Science Education, 86, 548–571.

O’Donnell, A. M., Dansereau, D. F. and Hall, R. H. (2002)

Knowledge Maps as Scaffolds for Cognitive Process-

ing. Educational Psychology Review, 14, 71–86.

Thagard, P. (1992). Conceptual Revolutions. Princeton

NJ:Princeton University Press.

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

148