Fast Algorithm of Short-time DCT for Low Resolution Signal

Processing

Vitaly Kober

Department of Computer Science, Division of Applied Physics, CICESE,

Carretera Ensenada-Tijuana No. 3918, Ensenada, B.C. 22860, Mexico

Keywords: Discrete Cosine Transform, Fast Algorithm.

Abstract: A fast algorithm for computing the discrete cosine transform (DCT) in a window running on a signal with a

step higher than one is proposed. The algorithm is based on a second-order recursive relation between DCT

spectra computed in windows which are equally spaced with a given distance. The computational

complexity of the proposed algorithm is compared with that of common fast and running DCT algorithms.

A fast inverse DCT transform is also presented.

1 INTRODUCTION

The discrete cosine transform (DCT) is widely used

in many signal processing applications such as

adaptive filtering, video signal processing, feature

extraction, and data compression. This is because the

DCT performs close to the Karhunen-Loeve

transform for the first-order Markov stationary data,

when the correlation coefficient is close to unity

(Jain, 1979).

In many applications, time-varying signals have

inherently infinite length. Since the signal properties

(amplitudes, frequencies, and phases) usually change

with time, a single orthogonal transform is not

sufficient to describe the entire signal. The concept

of short-time signal processing with filtering in the

domain of an orthogonal transform may be utilized

(Oppenheim & Shafer, 1989). A particular case of

the short-time processing is a local signal processing

in the domain of an orthogonal transform calculated

in a running window. The running orthogonal

transform of a signal x

can be defined as (Vitkus &

Yaroslavsky, 1987)

()

skpn

xns

=−

∑

(1)

where

()

{}

represents the basis of orthogonal

transform functions, k is integer value, p is the step

of the running window, and

displays the

orthogonal transform coefficients of the signal

around time

kp. A block-diagram of this processing

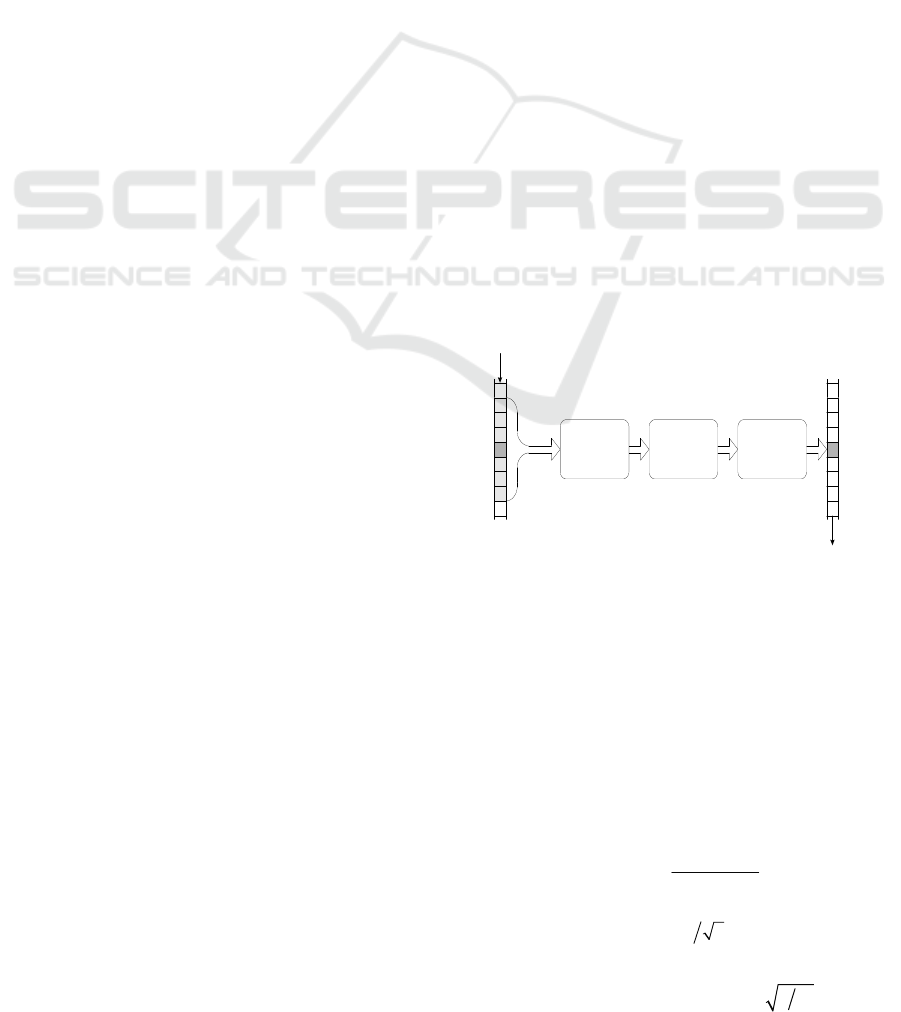
is illustrated in Fig. 1.

Figure 1: A block-diagram of local signal processing in

the domain of an orthogonal transform in a running

window.

The choice of orthogonal transform for running

processing depends on many factors. The DCT is

one the most appropriate transforms with respect to

the accuracy of power spectrum estimation from the

observed data that are required for local filtering, the

filter design, and computational complexity of the

filter implementation. The kernel of the DCT for the

order

N is defined as

(2)

where n, s=0,…, N-1,

For clarity, the normalization factor can be

OT Filtering

Inverse

input sequenc

output sequence

xn-N1

n+N2

()

⎧

⎫

⎛⎞

⎪

⎨

⎬

⎜⎟

⎪

⎝⎠

⎩⎭

cos

DCT k

12 0

⎧

⎪

⎨

⎪

⎩

if s

otherwise



2 N

Kober V..

Fast Algorithm of Short-time DCT for Low Resolution Signal Processing.

DOI: 10.5220/0004017800710074

In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems

(SIGMAP-2012), pages 71-74

ISBN: 978-989-8565-25-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

neglected until the inverse transform. The

computation of the DCT at each position of a

moving window is an intensive task. When the

window moves with a step of one, the shift

properties of discrete sinusoidal transforms may be

used for updating the transform coefficients. The

shift properties of the first-order were derived (Yip

and Rao, 1987). However, this approach is not very

efficient with respect to computational complexity.

The second-order recursive expressions and rapid

algorithms for the computation of the running DCT

with a step of one were suggested (Macias and

Exposito, 1998); (Kober and Cristobal, 1999); (Xi

and Chiraro, 2000); (Kober, 2004). In real

applications, it is often necessary to process a signal

with a high rate and a low resolution; for instance, in

order to obtain preliminary results for further data

analysis. In this case, signal processing in the

domain of the sliding DCT with a given arbitrary

step (higher that one) is appropriate technique.

In this paper, a fast recursive algorithm for

computing the DCT in a window running on a signal

with an arbitrary step with less computation than

that of known recursive and fast DCT algorithms is

proposed. Moreover, intervals for the window step

in which the proposed algorithm is more effective

than the fast DCT algorithms are calculated. A fast

inverse DCT transform is also presented.

2 RECURSIVE ALGORITHM

FOR COMPUTING RUNNING

DCT WITH ARBITRARY STEP

The running DCT with a step of p can be defined as

follows:

(

)

cos

=−

++⎛⎞

⎜⎟

⎝⎠

∑

skpn

nN s

(3)

where {x

; k =…, -N

, - N

+1,…, 0, 1,…, N

+1….} is an infinite-length signal,

{}

,0,1,...1=−

Xs N

are the transform coefficients

around time

kp, N= N

+ N

+1 is the length of the

running window. Here N is an arbitrary integer

value. For clarity, the normalization factor and

specific scaling of the

component are

neglected. The coefficients of the DCT can be

obtained as {

kp kp

;

kp kp

CX=

1, ... 1sN=−

}. A recursive relationship between

three consecutive running spectra

2−k

−

and

is given by (Kober, 2004)

12kkkk

ss s s

aX X f

−−

−+

(4)

where

()

(

)

21 1

11 22

skN kN kNkN

fx x x x

−− −− + + −

=−+− − x

(

)

cos 2

(

)

2cos

, and

This is a second-order liner inhomogeneous

difference equation defined on k. The roots of the

corresponding characteristic equation (Kelley &

Peterson, 1991; Mickens, 1990) are equal to

exp( )

j and exp( )

−

j . After some

manipulations, the general solution of the difference

equation (4) can be expressed as

()

() ( )

()() ()()

001

, 0

sin sin

sin sin sin ,

1, ... 1

km kk

sss

km kk

ss s ssk

ssss

kX k k mf X

mf s

Xkf mX

kk f m

αα

ααα

−

−+

−

−+

+− +

+−

−+

=−

⎧⎛ ⎛ ⎞⎞

⎜⎜ ⎟⎟

⎪

⎝⎝ ⎠⎠

⎪

⎛⎞

⎪

⎜⎟

⎝⎠

⎨

⎪

⎩

∑

(5)

where

and

are initial DCT spectra

computed at arbitrary window positions k

and k

< k

), respectively.

Since the window moves on a signal with a step

of p, the local spectra are calculated in equally

spaced window positions kp, where k is integer

value, and k> k

. In this case, a recursive relation

between three spectra

(2)−kp

X ,

(1)−kp

X , and

can

be obtained from equation (5) as follows:

()

(1) (2) (2) 1 1

(1) 1

(1) (2)

(2) 1 1

(1) 1

, 0

2cos

sin

,1,...1

sin

kp kp kpm kpm

ss s s

kp k p

kp s s s

kpm kpm

Xffm

fps

XpX

fsN

−

−− −++−+

−+

−−

−

−++ −+

−+

−

−+

=−

⎧

⎪

⎨

⎪

⎩

∑

(6)

We see that the computation of the DCT at the

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications

window position kp involves values of the input

signal x

as well as the DCT's coefficients computed

in two previous positions (k-1)p and (k-2)p of the

moving window. If p=1 the recursive equation is

simplified to one given in (4).

The number of arithmetic operations required for

computing the DCT with p>1 at a given window

position is evaluated as follows: if N is odd, the

complexity is N(p+1) multiplication operations and

N(p+1)+5(p-1) addition operations; if N is even,

from the property of symmetry of the functions

()()

(

)( )

sin sin sin sin

αα α α

−−

s s Ns Ns

and

() ()

11,1,...1,

−

−=− = −

sNs

1,...=mp, the

computational complexity with respect to

multiplication operations is reduced to N(p+3)/2.

The total number of required arithmetic operations

can be estimated as follows: 2N(p+1)+5(p-1) and

()()

355 1

++ −

when N is odd and even,

respectively.

Table 1: Comparison of algorithms for computing running

DCT in terms of arithmetic operations flops (real adds and

mults), N=256.

p-step of running

window

Algorithms

Fast DCT Recursive DCT Proposed DCT

1 3708 1024 1024

2 3708 2048 1413

3 3708 3072 1802

4 3708 4096 2191

5 3708 5120 2580

6 3708 6144 2969

7 3708 7168 3358

8 3708 8192 3747

9 3708 9216 4136

The recursive running DCT algorithm (Rosendo

et al., 1998); (Kober and Cristobal, 1999) requires

approximately 4Np arithmetic operations for

computing the DCT spectra in equally spaced

window positions kp. One can observe that the

proposed algorithm with p>1 is more effective than

the use of the sliding recursive algorithm. Table 1

shows numerical results of computational

complexity for the proposed, fast DCT (Johnson and

Frigo, 2007); (Shao and Johnson, 2008), and running

recursive algorithms (Rosendo et al., 1998); (Kober

and Cristobal, 1999) for N=256 when p is varied.

We see that the proposed algorithm yields better

results when the window step p is less than a

boundary value of 8. The boundary values for the

step versus the window length N are provided in

Table 2.

Table 2: Boundary values of the step p for the proposed

algorithm versus N.

N 16 32 64 128 256 512 1024

p 3 4 6 7 8 9 10

The length of a moving window for the proposed

algorithm may be an arbitrary integer value

determined by characteristics of the signal to be

processed.

The inverse algorithms for the sliding DCTs can

be written as follows:

(

)

1/ 2

2cos

xX X

−

⎛⎞

⎜⎟

⎝⎠

∑

(7)

where N=N

+1. The computational complexity is

N multiplication operations and N addition

operations. If x

is the central pixel of the window,

that is, N

and N=2N

+1, then the inverse

transform is given by

()

⎛⎞

=−+

⎜⎟

⎝⎠

∑

xXX

(8)

So, in the computation only the spectral coefficients

with even indices are involved. The computation

requires one multiplication operation and N

addition operations.

3 CONCLUSIONS

A rapid recursive algorithm for computing the DCT

in a window running on a signal with an arbitrary

step was proposed. The algorithm is based on a

recursive relationship between three consequent

local DCT spectra which are computed in equally

spaced signal windows. The computational

complexity of the algorithm was compared with that

of common fast and running DCT algorithms.

Intervals for the window step in which the proposed

algorithm is more effective than the fast DCT

algorithms were calculated. The algorithm can be

used for local signal processing with an arbitrary

resolution in the short-time DCT domain.

REFERENCES

Jain, A. K., 1979. ‘A sinusoidal family of unitary

transforms’, IEEE Trans. Pattern Anal. Machine

Intell., vol. PAMI-1, pp. 356-365.

FastAlgorithmofShort-timeDCTforLowResolutionSignalProcessing

Johnson, S. G. & Frigo, M. 2007. ‘A modified split-radix

FFT with fewer arithmetic operations’, IEEE Trans.

Signal Process., vol. 55, pp 111-119.

Kelley, W. G. & Peterson, A. C. 1991. Difference

equations. An introduction with Applications,

Academic, New York.

Kober, V. & Cristobal, G., 1999. ‘Fast recursive

algorithms for short-time discrete cosine transform’,

Electronics Letters, vol. 35, pp. 1236-1238.

Kober, V. 2004. ‘Fast algorithms for the computation of

sliding discrete sinusoidal transforms’, IEEE Trans.

Signal Process., vol. 52, pp. 1704-1710.

Mickens, R., 1990. Difference equations, Van Nostrand

Reinhold, New York.

Oppenheim, A. V. & Shafer, R. W., 1989. Discrete-time

signal processing, Prentice Hall, Englewood Cliffs NJ.

Rosendo Macias, J. A. & Gomez Exposito, A., 1998.

‘Recursive formulation of short-time discrete

trigonometric transforms’, IEEE Trans. Circuits. Syst.

II, vol. 45, pp. 525-527.

Shao, X. & Johnson, S. G. 2008. ‘Type-II/III DCT/DST

algorithms with reduced number of arithmetic

operations’, Signal Process., vol. 88, pp. 1553-1564.

Vitkus, R. Y. & Yaroslavsky, L. P., 1987. ‘Recursive

algorithms for local adaptive linear filtration’, in

Mathematical research, eds L.P. Yaroslavsky, A.

Rosenfeld & Wilhelmi, Academy Verlag, Berlin.

Xi, J. & Chiraro, J. F., 2000. ‘Computing running DCT's

and DST's based on their second-order shift

properties’, IEEE Trans. Circuits. Syst. I, vol. 47, pp.

779-783.

Yip, P. & Rao, K. P., 1987. ‘On the shift properties of

DCT’s and DST’s’, IEEE Trans. Acoust., Speech,

Signal Processing, vol. ASSP-35, pp. 404–406.

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications