
Mining Generalized Association Rules using Fuzzy Ontologies
with Context-based Similarity
Rodrigo Moura Juvenil Ayres
and Marilde Terezinha Prado Santos
Department of Computer Science, Federal University of São Carlos, Rod. Washington Luis, São Carlos, Brazil
Keywords: Generalized Association Rules, Fuzzy Ontologies, Post-processing, Context-based Similarity.
Abstract: In crisp contexts taxonomies are used in different steps of the mining process. When the objective is the
generalization they are used, manly, in the pre-processing or post-processing stages. On the other hand, in
fuzzy contexts, fuzzy taxonomies are used, mainly, in the pre-processing step, during the generation of
extended transactions. A great problem of such transactions is related to the generation of huge amount of
candidates and rules. Beyond that, the inclusion of ancestors in the same ends up generating problems of
redundancy. Besides, it is possible to see that many works have directed efforts for the question of mining
fuzzy rules, exploring linguistic terms, but few approaches have proposed new steps of the mining process.
In this sense, this paper propose the Context FOntGAR algorithm, a new algorithm for mining generalized
association rules under all levels of fuzzy ontologies composed by specialization/generalization degrees
varying in the interval [0,1]. In order to obtain more semantic enrichment, the rules may be composed by
similarity relations, which are represented at the fuzzy ontologies in different contexts. In this work the
generalization is done during the post-processing step. Other relevant points are the specification of a
generalization approach; including a grouping rules treatment, and an efficient way of calculating both
support and confidence of generalized rules during this step.
1 INTRODUCTION
An important task in data mining is the mining
association rules, introduced in (Agrawal et al.,
1993). In traditional algorithms of association, like
Apriori, the rules are generated based only on
existing items in the database. This characteristic
makes an excessive amount of rules be produced. In
this sense, the domain knowledge, represented via
taxonomies, can be used in order to obtain more
general patterns, facilitating the user’s
comprehension. The association task using
taxonomic structures is called mining generalized
association rules, and was introduced by (Srikant
and Agrawal, 1995) and (Jiawei Han and Fu, 1995).
According to the authors, ancestors of taxonomy
are inserted into database transactions, which are
called extended transactions. Then, from these
extended transactions, it is applied an algorithm for
extract the final set of rules, which can be composed
by traditional rules and generalized ones. However,
the inclusion of ancestors in the database
transactions results the generation of many candidate
itemsets, in addition, algorithms using such
transactions ends up generating redundant patterns,
making it extremely necessary the use of interest
measures for eliminate redundancies. On the other
hand, some works, like (Carvalho et al., 2007) for
example, show that the post-processing stage can be
more advantageous, because few candidates and
rules are generated. Moreover, it is eliminated the
need of measures used for prune redundant rules,
since the process is made based on the traditional
patterns generated.
However, in many applications of the real world
ontologies and taxonomies may not be crisp, but
fuzzy (Wei and Chen, 1999), because some
applications do not have classes of objects with
pertinence criteria precisely defined (Zadeh, 1965).
In this context, Wei and Chen (Wei and Chen, 1999)
introduced the use of fuzzy taxonomies. They
considered the partial relationships possibly existing
in taxonomies, where an item may partially belong
to more than one parent. For instance, tomato may
partially belong to both fruit and vegetable with
different degrees. Wei and Chen thus defined a
fuzzy taxonomic structure and considered the
extended degrees of support, confidence and interest
74
Moura Juvenil Ayres R. and Terezinha Prado Santos M..
Mining Generalized Association Rules using Fuzzy Ontologies with Context-based Similarity.
DOI: 10.5220/0004011300740083
In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 74-83
ISBN: 978-989-8565-10-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

measures for mining generalized association rules.
However, most of the works are focused in to
improve methods of to obtain generalized fuzzy
association rules, which are the ones composed by
linguistic terms, but few works have directed efforts
for improve the exploring of generalized rules under
fuzzy concept hierarchies, mainly in relation to the
stage that they are used.
Besides, some works, like (Miani et al., 2009)
and (Escovar et al., 2006), explore the semantic
enrichment through similarity relations. However,
these works do not consider that the degree of a
similarity relation, between two or more elements, it
is also related to the point of view or to the context
analysed. For example, consider the problem of
compare two vegetables, tomato and khaki, in
relation to two different points of view (contexts),
appearance and flavour. In respect to the appearance
context, would be possible to check that tomato is
very similar to khaki, with a very high degree of
similarity; but in relation to the flavour, would be
possible to check that both are bit similar, with a
minor degree of similarity.
Thus, this paper presents the Context FOntGAR
algorithm for mining generalized association rules,
using fuzzy ontologies composed by relationships of
specialization/generalization varying in the interval
[0,1], and similarity relations with different degrees
according to the context. The generalization can to
occur in all levels of fuzzy ontologies. The paper is
organized as follow: Section two shows some related
works. Section three presents the Context FOntGAR
algorithm. The section four presents the
experiments, and the section five shows the
conclusions.
2 BACKGROUND
Aiming to obtain general knowledge, the generalized
association rules, which are rules composed by items
contained in any level of a given taxonomy, were
introduced by (Srikant and Agrawal,1995). There
are many works using crisp taxonomic structures.
These works are distinguished, mainly, in function
of the stage (of the algorithm processing) in which
these structures are used.
In the pre-processing, the generalized rules are
obtained through extended databases, and these
bases are generated before the pattern generation.
Extended databases are the ones composed by
transactions containing items of the original
database and ancestors of the taxonomy. In the post-
processing the generalized rules are obtained after
the generation of the traditional rules, through a sub-
algorithm that uses some generalization
methodology based on the patterns generated.
In (Wu and Huang, 2011), the mining is made
using an efficient data structure. The goal is to use
the structure for find rules between items in different
levels of a taxonomy tree, under the assumption that
the original frequent itemsets and association rules
were generated in advance. Thus, the generalization
occurs during the post-processing step. In relation to
the post-processing, (Carvalho et al., 2007) proposed
the GARPA algorithm. The algorithm, unlike what
was proposed by (Srikant and Agrawal, 1995), do
not insert ancestor items in the database transactions.
The generalization was done using a method of
replacing rule items into taxonomy ancestors. From
the quantitative point of view, this process is more
advantageous than proposed by (Srikant and
Agrawal, 1995), because implies a smaller amount
of candidates, and consequently of rules generated,
dispensing the use of measures for pruning
redundant rules.
In mining generalized rules, most of the works
using fuzzy logic are mainly focused in to obtain
generalized fuzzy association rules, which are the
ones composed by fuzzy linguistic terms, such as
young, tall, and others. In such approaches are used
crisp taxonomies and the linguistic terms are
generated based on fuzzy intervals, normally
generated through clustering. Besides, these works
are directed to explore quantitative or categorical
attributes. In this context we can to point, for
example, the works (Hung-Pin et al., 2006),
(Mahmoudi et al., 2011), (Cai et al., 1998), (Hong et
al., 2003) and (Lee et al., 2008). On the other hand,
few works use fuzzy taxonomies in order to obtain
their rules. In this case, the focus is not the exploring
of patterns composed by linguistic terms, but it is
how to explore taxonomic structures composed by
different specialization/generalization degrees.
The problem of mining generalized rules using
fuzzy taxonomies was proposed by (Wei and Chen,
1999). They included the possibility of partial
relationship in taxonomies, i.e., while in crisp
taxonomies the specialization/generalization degrees
are 1, in fuzzy structures such degrees vary in the
interval [0,1]. So, the degree
which any node y
belongs to its ancestor x can be derived based upon
the notions of subclass, superclass and inheritance,
and may be calculated using the max-min product
combination. Specifically,
=max
∀: →
(min
∀
)
(1)
Where l: → is one of the paths of attributes
x and y, e on l is one of the edges on access l,
is
MiningGeneralizedAssociationRulesusingFuzzyOntologieswithContext-basedSimilarity
75

the degree on the edge e on l. If there is no access
between x and y,
=0 (Wei and Chen, 1999).
In addition to defining such structures, they also
consider extended degrees of support and confidence.
The degree of the extended support (Dsupport) is
calculated based on this
. If a is an attribute value
in a certain transaction t ∈ T, T is the transaction set,
and x is an attribute in certain itemset X, then, the
degree
can be viewed as the one that the
transaction {a} supports x. Thus, the degree that t
supports X may be obtained as follows:
=
=min
∀∈
(max
∀∈
))
(2)
Furthermore, an
∑
operator is used to sum
up all degrees that are associated with the
transactions in T, in terms of how many transactions
in T support X:
(
∀∈
) = (
∀∈
)
(3)
Thus, the support of a generalized association
rule X → Y, let X ∪Y = Z ⊆ I, can be obtained as
follows, where
|
|
is the total of transactions in the
database:
∑
(
∀∈
)/
|
|
(4)
Similarly, the confidence (X → Y), called
Dconfidence, can be obtained as follows:
∑
(
∀∈
)/
∑
(
∀∈
)
(5)
It is important to say in (Wei and Chen, 1999)
only the concepts are defined and in (Chen and Wei,
2002) the authors proposed two algorithms to realize
the mining, one working with the mentioned
taxonomies, and other working with these
taxonomies and linguistic terms. The first was called
FGAR, and the second was called HFGAR, both
algorithms use the same concept of extended
transactions.
A similar work can be found in (Keon-Myung,
2001), however, it is related to the mining
generalized quantitative association rules. The
authors use two different structures: fuzzy concept
hierarchies and generalization hierarchies of fuzzy
linguistic terms. In the first, a concept may have
partial relationship with several generalized
concepts, and the second is a structure in which
upper level nodes represent more general fuzzy
linguistic terms.
As well as Wei and Chen (Wei and Chen, 1999),
(Keon-Myung, 2001) also use the technique of
extended transactions. Besides, it is considered the
use of interest measures for prune redundant rules.
According to (Wen-Yang et al., 2010), the works
using fuzzy taxonomies, like proposed by (Wei and
Chen 1999), require the same be static, ignoring the
fact they cannot necessarily be kept unchanged. For
example, some items may be reclassified from one
hierarchy tree to another for more suitable
classification.
In this sense, the work (Wen-Yang et al., 2010)
introduces an algorithm where the final set of rules
generated can be updated according to the evolution
of the structures. The evolution can to occur due
four basic causes: insertion, deletion, renaming and
reclassification of items. Fuzzy taxonomies are used
and, as well as (Wei and Chen, 1999), (Keon-
Myung, 2001), and (Wen-Yang et al., 2010), the
generalized rules are obtained using extended
transactions.
Thus, in respect to the use of fuzzy taxonomies,
composed by degrees of specialization/
generalization varying in the interval [0,1], the
works (Wei and Chen, 1999) , (Keon-Myung, 2001),
and (Wen-Yang et al., 2010), are the most relevant
found in the literature.
On the other hand, some works, like (Escovar et
al., 2006) and (Miani et al., 2009) are directed to the
semantic of the data mined. They use ontologies for
extract associations of similarity existing between
items of the database. These relations are
represented in the leaves of ontology, but the
specialization/generalization degrees are constant 1,
like crisp ontologies. The work (Miani et al., 2009)
is an extension of (Escovar et al., 2006), and the
main differences are the introduction of a
redundancy treatment and a step of generalizing
non-frequent itemsets. However, both algorithms are
limited, since generalizes at only one level of
ontology (leaf nodes to parents).
As said, these works do not consider the question
of context in the similarities represented at the
leaves. In this line, the work (Cerri et al., 2010)
propose an Upper Fuzzy Ontology With Context
Representation (UFOCoRe), an approach that
represent multiple relationship strengths in a single
ontology, so that it is possible to express different
relationship semantics depending on the context
chosen. The approach does not define context
ontology like the ones used in context-aware
systems, but it allows organizing the context
information of multiple perspectives in single
domain ontology. As described, there are few works
dealing with mining generalized association rules
under fuzzy taxonomies. Besides, most of the works
are inserted in the line of mining generalized fuzzy
association rules, which is a concept smoothly
different, since for it are used crisp taxonomies and
the fuzzy generalized rules are obtained, most of the
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
76

time, with the utilization of linguistic terms. Besides,
it is possible to see a bias, which is the realization of
the generalization process exploring fuzzy
taxonomies during the pre-processing stage, through
extended transactions. In this sense, considering the
concept of fuzzy taxonomies, presented in (Wei and
Chen, 1999), no work to date was proposed for
obtain generalized rules during the post-processing
stage including the questions of similarity relations
considering context.
3 THE PROPOSED ALGORITHM
The aim of the Context FOntGAR is post-process a
set of specialized association rules (AR) using fuzzy
ontologies, in order to obtain a reduced non-
redundant and more expressive set of generalized
rules, facilitating the user’s comprehension. Figure 1
illustrates all steps of the Context FOntGAR
algorithm. The steps colored in grey are the main
points of our algorithm.
3.1 Main Ideas
The process of generating traditional association
rules is based on Apriori (Agrawal and Srikant,
1994), and as an mining association rule algorithm,
it needs of an user-provided minimum support and
minimum confidence parameters to run. Moreover,
it needs of a minGen, a side and a context
parameters:
• minsup, which indicates the minimum support;
• minconf, represents the mininum confidence;
• minGen, which represents the minimum quantity
of descendants in different specialized rules;
• minSim, which is the minimum similarity used
in the reasoner inferences (Miani et al., 2009);
• side, which represents the side of generalization;
• context, which represents the context used in the
similarity;
The minsup, minconf, minGen and minSim
parameters are expressed by a real value in the
interval [0,1]. The side parameter is expressed by a
string left, right or lr, indicating the generalization
side. The generalization can be done on one side of
the rule (antecedent or consequent) or both sides (lr:
left and right side). While the left side indicates
relations between classes of items and specialized
items, the side right indicates relations between the
specialized items and classes of items. The side lr
indicates relations between classes. The similarities
are represented in the leaves of ontology. Relations
with similarity degree value greater than or equal to
the user-provide minSim (Miani et al., 2009) can be
show in the rules generated, increasing the semantic
enrichment of the same. The generalization is made
through a sub-algorithm that uses a methodology of
grouping and replacement in the rules. In this
methodology, two or more rules are grouped in order
to be replaced by a unique generalized rule. Several
groups can be generated, and the grouping is done
based on the parameter side and on the fuzzy
ontology. In this case, two or more rules having
identical parents in the side of generalization are
grouped in a same group.
It is important to say that a group is generated
only if two or more rules can be grouped, because is
not reasonable generalize a unique rule. As several
groups may be generated, various generalized rules
may be obtained. During the grouping, the ancestors
analyzed are the immediate ones of items present on
rules in question, which are the ancestor presents in
the current level of generalization. The parameter
side indicates the generalization side. Thus, when
this parameter is set with left or right, if two or more
rules have the same elements in the opposite of side,
and have identical parents in relation to the items
present in the side, then these rules are placed in a
same group. For example, supposing ontology of
bread and milk, where bread is a breadA, breadB,
breadC, breadD, breadE, and milk is a milkA, milkB
milkC. Suppose the algorithm generates, during the
extracting patterns stage, a set of traditional rules
milkA → breadA, milkA → breadB, milkA
→
breadC, which are the ones composed only by leaf
nodes.
Figure 1: Steps of the Context FOntGAR.
When the parameter side is lr, if two or more rules
have the same parents in relation to the
MiningGeneralizedAssociationRulesusingFuzzyOntologieswithContext-basedSimilarity
77

Figure 2: Pseudo-code of generalization.
antecedent items, and, respectively, have the same
parents in relation to the consequent items, then
these rules will be grouped together. For example,
considering that traditional rules milkA → breadA,
milkB → breadB, milkC → breadC have been
generated. Comparing these rules, we can see that
they have the same parent in relation to the
antecedent, and respectively, they have the same
parent in relation to the consequent. Thus, these
rules will be grouped together.
It is important to say the rules used in the
grouping can be composed by any quantity of items.
At first, the patterns used during the generalization
are the traditional ones generated by the extracting
patterns stage. Posteriorly, the obtained generalized
rules are treated in the same way, in order to obtain a
new set of generalized rules. Thus, it is a recursive
process. An important point is that generalized rules
can be generated without the use of all descendants
of an ancestor. In this sense, to avoid an over-
generalization, a set of specialized rules contained in
a group can be substituted by a more general rule
only if a minGen parameter (Miani et al., 2009) was
satisfied. Consider that the minGen value is 0.6
(60%), and the side is lr, the rule milk → bread will
be generated even if there is no rule for each kind of
bread and milk in the current group, but only if 60%
of descendants of bread and milk are present in this
set of rules. Thus, the use of minGen could produce
a semantic loss. In this sense, in order to guide the
user’s comprehension, the algorithm show the items
which have not participate in the generalization
process. For example, suppose the item breadE is
not present in the specialized AR set, the generalized
rule are shown as milk → bread (-breadE),
indicating that the item breadE did not compose the
generalization.
In this research, for represent a fuzzy ontology
with specialization/generalization degrees varying in
[0,1] and context in similarity relations, we follow
the ideas described in two meta-ontologies,
proposed in (Agrawal and Srikant, 1994), and (Cerri
et al., 2010) respectively. Both are upper ontologies
as it represent fuzzy constructs to be inherited and/or
instantiated by specific domain ontologies. Such
ontologies are based on OWL DL (Smith et al.,
2004), a W3C recommendation supported by several
reasoners and application programming interfaces
used to develop ontology-based applications.
3.2 The Algorithm Step by Step
First, the ontology reasoner is used to infer the
membership degrees of the leaves in relation to the
ancestors, through the equation 1 of the section two.
These degrees are stored in a data structure. The
steps of data scanning, generating candidates and
generating rules are done similarly to the Apriori.
At end of generating rules we have a set of
specialized rules, which will be used on the
generalization treatment. Then, the generated rules
and the side of generalization are passed to the
groupingRules function (line 7), which is
responsible by the grouping treatment mentioned
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
78

above. Posteriorly, for each group generated, all
rules in a group are represented by a more general
rule (line 10). So, the minGen parameter (line 11) is
checked, besides, it is verified if antecedent ∩
consequent = 0 and if no consequent item is ancestor
of any antecedent item (line 12). If such verifications
are satisfied (line 13), the calculus of support is
done. If the general rule is not frequent then the
generalization is not made. In this case, if the level is
1 (line 19), the rules of the corresponding group are
inserted in the result. But if the general rule is
frequent, the rules of the corresponding group are
replaced by the same, and it is inserted in the result.
After that, if there are generalized rules, the same
are used in the next level of generalization. If this
situation is true for all next levels, the generalization
process will be done until a level below the ontology
root. However, if there is no generalized rule at a
certain level, then will be impossible generalize in
the next levels. When this happens, the
generalization process is concluded. After the
generalization treatment, the algorithm uses the
ontology reasoner to obtain the similarity relations.
So, these relations are used in the non-generalized
rules. Finally, after that, the algorithm enters its final
stage, which is the results generation.
3.3 Calculating the Support and
Confidence Degrees
Considering the fuzzy taxonomy of Figure 3, Fruit
→ Meat is a generalized rule and {Fruit, Meat} is
their itemset format. The support is calculated based
on the sum of all degrees of transactions that support
simultaneous occurrences of {Fruit, Meat}.
However, {Fruit, Meat} is obtained and known only
during the post-processing. Then, for obtain the
degree of each transaction, it would be necessary a
new scanning in the database. As many generalized
rules may be generated, the quantity of new
scanning also may be huge, and depending on the
quantity of rows of the database, the performance of
the algorithm would be affected.
In Context FOntGAR we use two data structures
(Figure 3 and Figure 4) to allow the calculating of
support avoiding additional scan. Such structures are
composed by keys and values. In Figure 3, a key is
an item of the database or an ontology ancestor.
Each key points a value, which is a vector storing
the transaction identifiers where the key appear. The
vector is an object of the class Vector in Java,
dynamically created. The equation used in the
calculus of support is derived of the Equation 2
(section two). So, if we partitioned the same in two
subparts (Part 1 and Part 2), we have:
• Part 1 = max
∀∈
(
)
• Part 2 =min
∀∈
().
As said, we can have many generalized rules, but
we don’t know what will be generated. So, the
itemset format of each may be any X = {
,…,
},
where X is the generalized rule, and
,…,
are
items of the rule. That way, during the first scan, we
do the computation of Part 1, which is the degree
that each transaction t supports an ancestor x. Based
on the results of Equation 1, found at beginning of
the algorithm, these degrees are calculated and
stored in a data structure (Figure 4), where a key is
the ancestor x (which will be present in generalized
rules), and each key points a value, which is a vector
storing the degrees mentioned. Thus, since the result
of Part 2 correspond to min operator for the degrees
related to any rule {
,…,
}, we use the stored
degrees of
,…,
for calculating the Part 2,
obtaining the support of any generalized rule.
An important point is that if
=0 the
transaction does not supports
, then the degree
is not stored in the vector. Thus, each vector linked
in a key of the Figure 3 has the same quantity of
positions of the vector pointed out by the same key
of the Figure 4. Besides, in such vectors, the values
of correspondent positions are related. For example,
through Figure 3 we can see that the key Fruit is
present in three transactions, T1, T2 and T4. Then,
from the Figure 4.5 we can infer that the degree
which T1, T2 and T3 support Fruit is 1, 0.7 and 0.7,
in the same order.
Figure 3: Indexing items and ancestors.
Now, consider an example about how calculate
the support of the rule Fruit → Meat: First, the
algorithm uses the structure shown in the Figure 3
for verify the quantity of transactions in the
MiningGeneralizedAssociationRulesusingFuzzyOntologieswithContext-basedSimilarity
79

Figure 4: Storing the transaction support degrees.
Figure 5: Idea used in the calculating of support.
intersection of values stored in vectors of these keys,
since it represents all simultaneous occurrences of
Fruit and Meat on the dataset transactions. Figure 5
illustrates this idea. In this case we have two
occurrences of {Fruit, Meat}.
Then, in relation to each key, the algorithm uses
the positions of these transactions in Figure 3 to
found the degree which each transaction supports
these ancestors. Such degrees are present in the same
positions of the vectors linked at Fruit and Meat on
the Figure 4. In this case we have: Fruit: 0.7/T2,
0.7/T4; Meat: 0.6/T2, 1/T4, which are results of Part
1. Based on these degrees, we use Part 2 to calculate
the
, where X is {Fruit, Meat}.
For T2 we have:
=min
∀∈
(1)=min
(
0.7,0.6
)
=0.6
For T4 we have:
=min
∀∈
(1)=min
(
0.7,1
)
=0.7
So, according to Equation 3, we have 0.6 + 0.7 =
1.3. Furthermore, the Equation 4 is used to calculate
the support, which is 0.21. Although we presented a
specific example, the process applies to any rule.
3.4 Inferring Similarity Relations
According to the Context
As said before, for represent our fuzzy ontology, we
follow the ideas described in two meta-ontologies,
proposed in (Agrawal and Srikant, 1994), and (Cerri
et al., 2010). The approach proposed in (Cerri et al.,
2010) allows to represent, in a single ontology,
distinct relationships according to different contexts.
In relation to fuzzy relationships, they introduce
the ctx:ContextFuzzyRelationMembership class,
responsible for associating fuzzy relationships to
several contexts.
Ctx:ContextFuzzyRelationMembership is
subclass of the fuzz:FuzzyRelationMembership class
from the fuzzy ontology, thus it inherits
fuz:fuzzyRelationDomain, fuz:fuzzyRelationRange,
fuz:fuzzyRelationProp and fuz:membershipDegree
properties. The context association is represented by
ctx:hasContext and ctx:context properties, which
link contexts to fuzzy relationships
(fuz:FuzzyRelation) and fuzzy degrees respectively.
By using such constructs, a domain expert can
model fuzzy relationships from different
perspectives, with specific fuzzy degrees according
to each context.
In our algorithm, the similarity degree values
between items are represented in the fuzzy ontology
leaves, which specify the semantics of the database
contents. This step navigates through the fuzzy
ontology structure to identify semantic similarity
between items, according to the pre-defined context
parameter. If according to a user-provide context the
similarity degree between items is greater than or
equal to the minSim parameter cited in section 3.1, a
semantic similarity association is found and this
association is considered similar enough. A fuzzy
association of size 2 is made by these pair of items
found and are expressed by the symbol ~ indicates
the similarity relation between items, for example,
~
.
After that, this step verifies the presence of
similarity cycles as proposed in (Escovar et al.,
2005). These are fuzzy associations of size greater
than 2 that only exists if the items are, in pairs,
sufficiently similar. The minimum size of a cycle is
3, and the maximum is the number of sibling leaf
nodes, for example,
~
~
.
According to (Escovar et al., 2005), based on the
concept of fuzzy intersection, the similarity degree
value of a cycle is the minimum value found among
the pairs. For example, if in a context
~
are 0.8 similar;
~
are 0.7 similar;
~
are 0.5 similar, then
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
80

~
~
are 0.5 similar. Similarity
cycles are obtained through the transitive property
(Zadeh, 1965). All similarity relations and similarity
cycles with degree values greater than or equal to the
minsim are stored (as strings) by the algorithm. After
that, this step does a search in the rules generated
checking if the same have items that are included in
some relation or cycle stored. In positive cases, these
items are replaced by the correspondent string
stored. We can say the positive cases are related to
the traditional rules which have not been
generalized, since the similarity relations are
associated only to the leaf nodes. For example,
suppose the rule:
,
→
,
. Considering that there is a similarity relation
~
, then the stored correspondent string,
~
, it is inserted in the rule, replacing the
single items
and
. So only the new
rule,
~
,
→
,
, it is
show by the algorithm.
We can say that our approach is totally different
than (Miani et al., 2009) and (Escovar et al., 2006).
In these works, the inclusion of similarities in the
rules is done through a concept of fuzzy item, which
are a type of similarity representation. Such items
are inserted in the set of candidates, during the
candidate generation, and are used to generate the
rules. Besides, a calculus of fuzzy occurrences also
is done. Another different point is that (Miani et al.
2009) and (Escovar et al., 2006) do not consider the
inclusion of context in the similarity relation.
4 EXPERIMENTS
This section shows some experiments performed to
validate the Context FOntGAR algorithm. Two real
datasets were used. The first dataset (DB-1) contains
information about Years of study, Race or ethnicity
and Sex, and was provided by Brazilian Institute of
Geography and Statistics (IBGE). DB-1 contains
10000 transactions with 12 distinct items. The
second data set (DB-2) contains a one day sale of a
supermarket located in São Carlos city. DB-2
contains 1716 transaction with 1936 distinct items.
Two fuzzy ontologies were created, one for the
DB-1, called Ont-1 ontology, and other for the DB-
2, called Ont-2 ontology. The Ont-1 was constructed
contained one level of abstraction, except by the
root, and Ont-2 was constructed with four levels of
abstraction, except by the root. In both ontologies
the average value of specialization/generalization
degrees was 0.8. Both ontologies were modeled in
OWL (Web Ontology Language) and the Jena
Framework was used to allow navigation through
ontology concepts and relations.
In order to compare and illustrate the
performance of Context FOntGAR, the experiments
were carried out with respect to two major aspects.
First, with the DB-1, the GARPA algorithm
(Carvalho, Rezende et al. 2007) under a
corresponding crisp taxonomy, NARFO (Miani et al.
2009) under a corresponding crisp ontology and
Context FOntGAR algorithm under the Ont-1 were
run. The purpose was to show what the effect of
fuzzy extensions could be. In this comparison, 2
experiments have been conducted. Second, with the
DB-2 and Ont-2, the Context FOntGAR was
executed. The purpose was to show how the
generalization treatment could improve the reduction
in the rules amount. This experiment checks the
compaction rate, which represents the percentage of
reduction in the volume of rules.
4.1 Performance Comparisons
We performed 2 experiments with real data and
taxonomic structures mentioned above, changing a
different parameter in each experiment. The
experiments were done with default values of
parameter, except for the one being varied. By
default, minsup = 0.02, minconf = 0.4 and mingen =
0.2. The side of generalization was set to lr in all
algorithms.
Number of Transactions
In Figure 6, the vertical axis is the average of
reading time per transaction (in milliseconds) in
relation to the first scanning in the database. Here
was compared the first scan on NARFO and the first
scan on Context FOntGAR. We varied the number
of transactions from 2000 to 10000. From Figure 6,
it is possible see that the gap between Context
FOntGAR, and NARFO show that the scanning with
fuzzy ontologies is more time consuming than
scanning with crisp ontologies. There are two
reasons. First, the membership degree calculation
demands more time. Second, the data structures
generation contributes for increase the runtime.
However, we can see that the gap tends keep stable
with the increase of the number of transactions. This
shows that the computational complexity is linear
with the number of transactions, which is the same
as the crisp algorithm. The difference between the
two curves turns to be constant.
In Figure 7 we changed the minimum degree of
support from 0.05% to 0.2%. The vertical axis is the
MiningGeneralizedAssociationRulesusingFuzzyOntologieswithContext-basedSimilarity
81
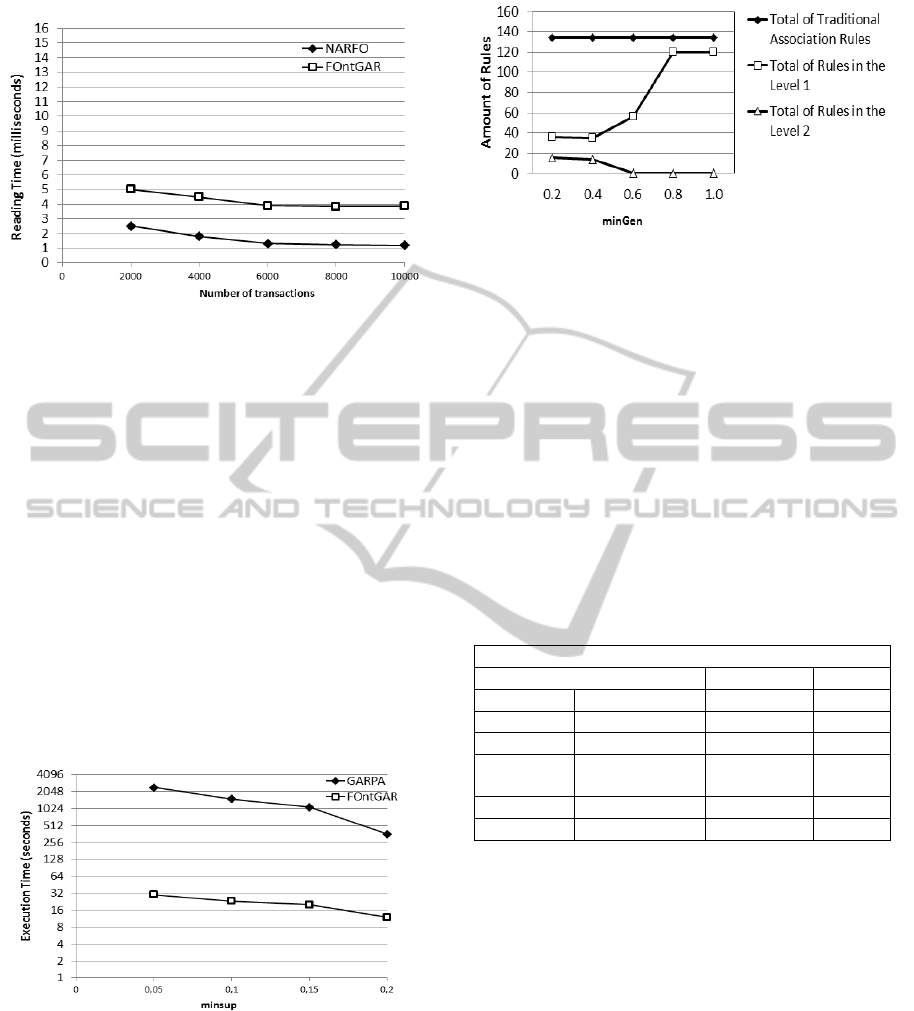
Figure 6: Scanning time (per transaction).
Minimum Degree of Support
total execution time in seconds. Notably, with the
increase of minsup, the runtime of both Context
FOntGAR and GARPA decreases. The reason is that
when the minsup increases the amount of traditional
rules decrease, and consequently a minor quantity of
rules are post-processed. However, we can see that
GARPA consumes more time than Context
FOntGAR. The reason is that GARPA demands
more time during the calculating of support, because
a new scan is done in the database for each
generalized rule obtained. So, depending on the
quantity of rules and rows of the dataset, the runtime
can be very high. On the other hand, apart from
provide an indexed access to data, in Context
FOntGAR, the data structures avoid the necessity of
new scans in the database, decreasing the runtime.
Figure 7: Comparison in relation to the runtime.
Compaction Rate in Context FOntGAR
The Figure 8 shows that the compaction rate is
high, especially when values of minGen are low.
This means that for high values of minGen the
number of generalized rules decreases and
consequently the number of traditional rules
increases, reflecting in the amount generated.
Figure 8: Compaction rate in Context FOntGAR.
4.2 Exploring Rules with Similarity
Relations
In order to explore rules with similarity relations the
DB-2 and Ont-2 were used. For explore different
contexts Ont-2 was extended through the meta-
ontology mentioned above. Two contexts were
inserted, flavour and appearance. The Table 1 shows
some leaf items and their respective similarity degree
values, in relation to the two contexts. The part shown
represents the similarTo relationship between the
spinach and mustard according to context appearance.
The similarity degree is set to 0.7.
Table 1: Similarity Degree Values.
Similarity Contexts
items Appearance Flavour
Coca-Cola Pepsi 0.8 0.6
Pepsi Brazilian Coke 0.8 0.5
Tomato Khaki 0.7 0.3
European
Chocolate
Brazilian
Chocolate
0.8 0.6
spinach lettuce 0.7 0.4
spinach mustard 0.7 0.4
In Table 1 the similarity degree values are given
in pairs of items. For example, spinach and mustard
have similarity 0.7 in context of appearance.
Besides, based on the table 1 two similarity cycles
can be found in the ontology. Depending on the
similarity value, the selection of context may cause
change in the similarities represented in the rules.
Our experiment was carried out employing the
parameters values: minimum support (minsup) =0.2,
minimum confidence (minconf)=0.2, and minimum
similarity (minsim)=0.3. Some examples of rules
generated are:
Appearance Context:
• spinach~lettuce~mustard, coffee → onion, potato
• tomato~khaki, bread → soap, detergent
• milk → EuropeanChocolate~BrazilianChocolate
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
82

5 CONCLUSIONS
This paper proposes the Context FOntGAR
algorithm, a new algorithm for mining generalized
association rules under all levels of fuzzy ontologies,
including similarity relations in the rules. The
experiments show that Context FOntGAR makes an
efficient generalization treatment, reducing the
amount of rules. This work presents several
contributions. First, it is introduced an algorithm
which uses fuzzy ontologies with context-based
similarity relations during the post-processing stage.
Considering the bias found in the literature, our
algorithm makes an important improvement on the
state of the art. Another important contribution is
that Context FOntGAR improves the semantic in the
rules and generates non-redundant patterns without
use pruning measures, since the generalized ones are
obtained based on the traditional rules. For future
works we are doing some improvements in the
Context FOntGAR algorithm. We are improving the
use of mingen, based on the user’s preferences.
ACKNOWLEDGEMENTS
We wish to thank the Determinants of Educational
Performance Project (CAPES/INEP).
REFERENCES
Agrawal, R., T. Imielinski, et al. (1993). Mining
association rules between sets of items in large
databases, Washington, DC, USA, ACM.
Agrawal, R. and R. Srikant (1994). Fast algorithms for
mining association rules. Conference on Very Large
Databases (VLDB). Santiago, Chile, Morgan
Kaufmann Publischers Inc.: 487-499.
Cai, C. H., Ada, et al. (1998). Mining Association Rules
with Weighted Items. International Database
Engineering and Application Symposium.
Carvalho, V. O. D., S. O. Rezende, et al. (2007).
Obtaining and evaluating generalized association
rules. 9th International Conference on Enterprise
Information Systems, ICEIS 2007, Funchal, Madeira;
12 June 2007 through 16 June 2007.
Cerri, M. J., C. Yaguinuma, et al. (2010). UFOCoRe:
Exploring Fuzzy Relations According to Specifics
Contexts. International Conference on Software
Engineering & Knowledge Engineering (SEKE 2010).
San Francisco Bay, USA: 529-534.
Chen, G. and Q. Wei (2002). "Fuzzy association rules and
the extended mining algorithms." Information
Sciences - Informatics and Computer Science: An
International Journal 147(1-4): 201-228.
Escovar, E. L. G., M. Biajiz, et al. (2005). "SSDM: A
Semantically Similar Data Mining Algorithm." 20
Brazilian Symposium of Databases.
Escovar, E. L. G., C. A. Yaguinuma, et al. (2006). Using
Fuzzy Ontologies to Extend Semantically Similar Data
Mining. 21 Brazilian Symposium on Databases.
Florianópolis, Brazil: 16-30.
Hong, T. P., K. Y. Lin, et al. (2003). "Fuzzy data mining
for interesting generalized association rules." Fuzzy
Sets and Systems 138(2): 255-269.
Hung-Pin, C., T. Yi-Tsung, et al. (2006). A Cluster-Based
Method for Mining Generalized Fuzzy Association
Rules. Innovative Computing, Information and
Control, 2006. ICICIC '06. First International
Conference on.
Jiawei Han and Y. Fu (1995). Discovery of Multiple-Level
Association Rules from Large Databases. 21º VLDB
Conference. Zurich, Switzerland: 420-431.
Keon-Myung, L. (2001). Mining generalized fuzzy
quantitative association rules with fuzzy generalization
hierarchies. IFSA World Congress and 20th NAFIPS
International Conference, 2001. Joint 9th.
Lee, Y.-C., T.-P. Hong, et al. (2008). "Multi-level fuzzy
mining with multiple minimum supports." Expert
Systems with Applications: An International Journal
34(1): 459-468.
Mahmoudi, E. V., E. Sabetnia, et al. (2011). Multi-level
Fuzzy Association Rules Mining via Determining
Minimum Supports and Membership Functions.
Intelligent Systems, Second International Conference
on Modelling and Simulation (ISMS), 2011.
Miani, R. G., C. A. Yaguinuma, et al. (2009). NARFO
Algorithm: Mining Non-redundant and Generalized
Association Rules Based on Fuzzy Ontologies.
Enterprise Information Systems. J. Filipe and J.
Cordeiro, Springer Berlin Heidelberg. 24: 415-426.
Smith, M. K., C. Welt, et al. (2004). "W3C Proposed
Recomendation: OWL Web Ontology Language
Guide." Retrieved 2 dezembro, 2010, from
Srikant, R. and R. Agrawal (1995). Mining Generalized
Association Rules. Proceedings of the 21th
International Conference on Very Large Data Bases,
Morgan Kaufmann Publishers Inc.
Vo, B. and B. Le (2009). "Fast Algorithm for Mining
Generalized Association Rules." International Journal
of Database Theory and Application 2(3): 1-12.
Wei, Q. and G. Chen (1999). Mining generalized
association rules with fuzzy taxonomic structures.
Fuzzy Information Processing Society, 1999. NAFIPS.
18th International Conference of the North American.
Wen-Yang, L., T. Ming-Cheng, et al. (2010). Updating
generalized association rules with evolving fuzzy
taxonomies. IEEE International Conference on Fuzzy
Systems (FUZZ), 2010.
Wu, C.-M. and Y.-F. Huang (2011). "Generalized
association rule mining using an efficient data
structure." Expert Systems with Applications 38(6):
7277-7290.
Zadeh, L. A. (1965). "Fuzzy sets." Information and
Control 8(3): 338-353.
MiningGeneralizedAssociationRulesusingFuzzyOntologieswithContext-basedSimilarity
83
