HaF
A New Family of Hash Functions
Tomasz Bilski, Krzysztof Bucholc, Anna Grocholewska-Czurylo, Janusz Stoklosa
Institute of Control and Information Engineering, Poznań University of Technology
pl. Marii Sklodowskiej Curie 5, Poznan, Poland
Keywords: Security, Privacy, Trust, Hash Functions, S-box design.
Abstract: Paper presents a family of parameterized hash functions allowing for flexibility between security and
performance. The family consists of three basic hash functions: HaF-256, HaF-512 and HaF-1024 with
message digests equal to 256, 512 and 1024 bits, respectively. Details of functions' structure are presented.
Method for obtaining function's S-box is described along with the rationale behind it. Security
considerations are discussed.
1 INTRODUCTION
In many cryptographic applications it is necessary to
generate a shortened form of a much longer
message. The shortened form called digest of the
message or hash value, is produced by means of a
hash function. A hash function h operates on an
arbitrary- length message m and returns a hash value
h(m) of a fixed length. Cryptographic hash functions
have many information security applications. We
use hash function to verify message integrity. Keyed
hash function is used for message authentication.
Recently we can see substantial effort in
designing of new cryptographic hash functions. For
example, as many as 64 proposals were submitted to
NIST SHA-3 competition, for new hash function, in
October 2008 (Regenscheid, 2009).
Our objective is to ensure that the security of
HaF is high and its performance is significantly
satisfactory.
The paper is organized as follows: Section 2
presents general overview of the family of
algorithms. Method for obtaining function's S-box,
along with the rationale behind it, is described in
Section 3. In Section 4 we discuss security
considerations. Section 5 is devoted to reference
implementation and the algorithm performance.
Concluding remarks are presented in Section 6.
2 PARAMETERIZED FAMILY
HaF OF HASH FUNCTIONS
2.1 Design Principles
The following assumptions were taken into account
during design process:
 the family should be parameterized;
 message digest length should be selectable;
 flexibility between performance and security
should be guaranteed;
 iteration structure and compression function
should be resistant to known attacks;
 its iteration mode should be HAIFA (it provides
resistance to long message second preimage attacks,
and handles hashing with a salt) (Biham, 2006).
2.2 Description of HaF
The HaF family is formed of three hash functions:
HaF-256, HaF-512 and HaF-1024, producing hash
values (message digests) with the length equal to
256, 512 and 1024 bits, respectively. The general
model for HaF is based on Merkle-Damgård
paradigm proposed by Biham and Dunkelman
(Menezes, 1997); (Biham, 2006) (Figure 2.1).
After formatting the original message m we have
the message M. We divide M into blocks M
0
, M
1
,…,
M
k–1
, k ∈ {1,2,…}, and each block M
i
is processed
with the salt s by the iterative compression function
188
Bilski T., Bucholc K., Grocholewska-Czurylo A. and Stokłosa J..
HaF - A New Family of Hash Functions.
DOI: 10.5220/0003825401880195
In Proceedings of the 2nd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2012), pages 188-195
ISBN: 978-989-8565-00-6
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

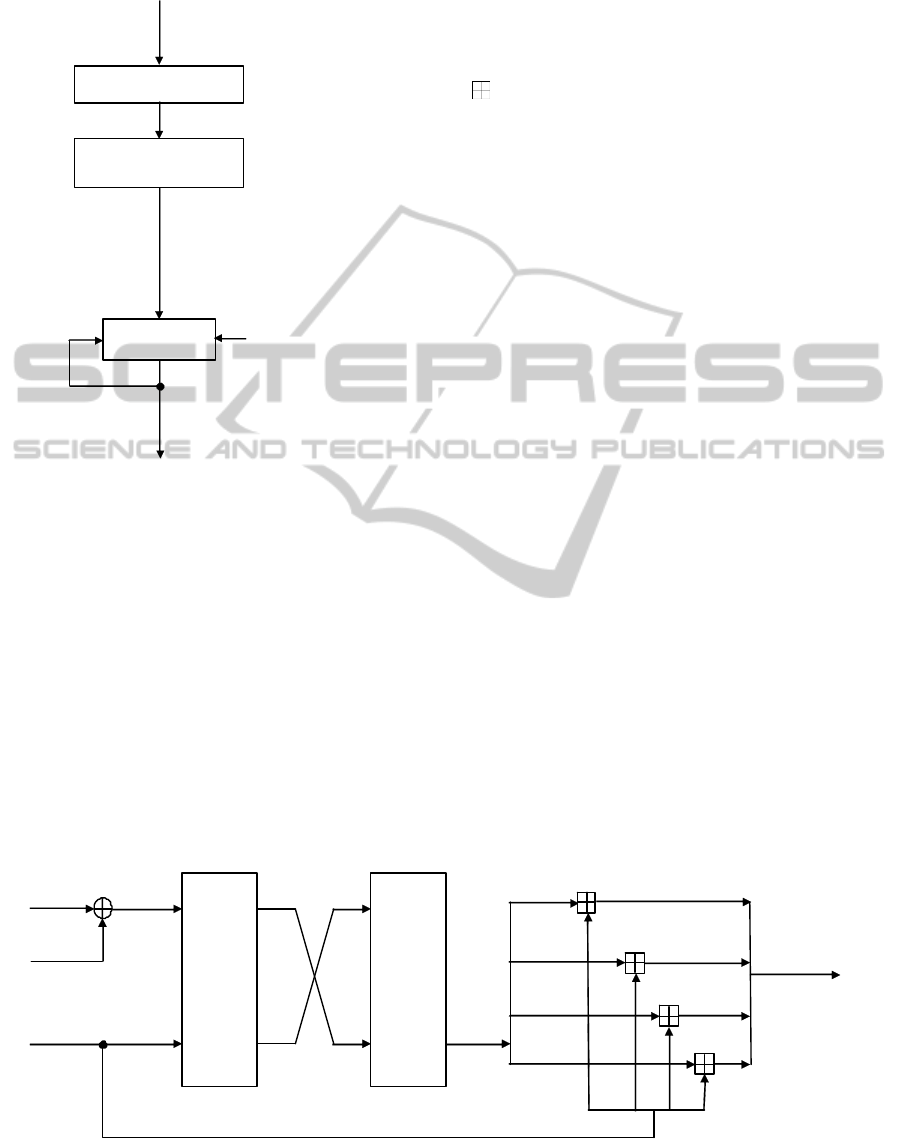
 (Biham, 2006). The output H
k
is the final result of
the function.
Append padding bits
Append length string
m
Formatted message
M = M
0
|| M
1
|| …|| M
k–1
φ
H
i
M
i
H
i+1
h(m) = H
k
H
0
=IV
s
Figure 2.1: General model for HaF.
2.2.1 Notation
In the paper we use the following notation:
a ⊙ b – multiplication mod (2
n
+1) of n-bit non-zero
integers a and b;
A
r
– working variable, r = 0, 1,…, 15;
F
j
– step function, j = 0, 1,…, 15;
GF(2) – Galois field of characteristic 2;
length – bitstring representing the length of the
original message m, |length| = 128;
lsb
q
(v) – q least significant bits of the string v;
IV – initial value;
m – original message, |m| < 2
128
;
M – formatted message;
n – length of the working variable A
r
(16 or 32 or 64
bits);
s – salt, |s| = 16n;
|v| – length in bits of a string v;
v << t – t-bit left rotation of a string v, |v| = 16n;
v ⊕ w – bitwise XOR of strings v and w, |v| = |w|;
v w – addition mod 2
n
of integers represented (in
base 2) by strings v and w;
p
1
(x) ⊗ p
2
(x) – multiplication of polynomials p
1
and
p
2
modulo an irreducible polynomial R(x);
x
q
– bitstring of the length q; x
0
means the empty
string;
 – compression function;
|| – concatenation of bitstrings.
2.2.2 Message Padding
The original message m has to be formatted before
hash value computation begins. The length of
formatted message should be a multiple of 16n bits.
The message m is formatted by appending to it a
single 1-bit and as few 0-bits as necessary to obtain
a string whose bit-length increased by 128 bits is a
multiple of 16n. Finally we must additionally
append original message length. As a result we
obtain the formatted message M = M
0
|| M
1
||. . .|| M
k–
1
for some positive integer k, where M
i
is a block of
M. Therefore, M = m || 10
t
|| length, where t is the
smallest nonnegative integer necessary to format m,
and |M| = 16nk.
2.2.3 Compression Function
In the proposed schema the compression function is
defined as follows: : {0,1}μ × {0,1}η × {0,1}σ →
{0,1}ρ. The integers μ, η and σ are lengths of block
Mi, chaining variable Hi, and salt s, respectively,
where |Mi| = |Hi| = |s| = 16n and i = 0, 1,…, k–1. The
integer ρ is the length of the resulting hash value
h(m) = Hk, |h(m)| = 16n.
Round
#2
N
i
*
H
i
*
N
i
H
i
H
i
*
A
15
H
i+1
16 ·n bit
s
A
15
...
A
2
A
1
A
0
...
A
2
A
1
A
0
Round
#1
s
H
i
16·n bits
16 ·n bit s
M
i
N
i
...
Figure 2.2: Method of one block processing.
HaF - A New Family of Hash Functions
189

The block M
i
is processed in two rounds. The
length of the block equals 16n bits, where n is a
parameter depending on the hash value we want to
obtain. For HaF-256, HaF-512 and HaF-1024 the
parameter n equals 16, 32 and 64 bits, respectively.
The parameter n indicates in fact the length of the
working variable A
r
used in the step function.
The method of one block processing is depicted
in Figure 2.2. M
i
, H
i
and s are inputs for  . Before
processing in round #l, l = 1 or 2, the block M
i
is
modified. In the round #1 four least significant bits
of N
i
= M
i
⊕ s indicate the number of bits the string
N
i
is rotated to the left: N
i
*
= N
i
<< lsb
4
(N
i
). Before
processing in the round #2 the blocks are permuted:
N
i
= H
i
*
and H
i
= N
i
*
. After two rounds, the value H
i
*
of chaining variable is split into 16 subblocks A
0
, A
1
,
…, A
15
of equal lengths. Each of them is modified by
adding (mod 2
n
) the respective input subblock of H
i
which is the input to the round #1. Next, all
subblocks A
0
, A
1
, …, A
15
are concatenated giving
H
i+1
= A
0
|| A
1
|| … || A
15
.
2.2.4 Round Function
The round function (Fig. 2.3) has two inputs N
i
, H
i
and two outputs N
i
*
, H
i
*
. The input block N
i
is
rotated by the number of bits corresponding to
lsb
4
(N
i
) and added (mod 2 of respective bits) to H
i
.
Next the block H
i
⊕ (N
i
<< lsb
4
(N
i
)) is divided into
16 subblocks of equal length: A
0
, A
1
, …, A
15
. They
are processed by a step function. After processing
they are concatenated giving H
i
*
. The output N
i
*
= N
i
<< lsb
4
(N
i
).
F
j
R
ound # l
A
2
A
1
...
A
0
A
15
A
2
A
1
...
A
0
A
15
16 steps
H
i
*
<<
lsb
4
(N
i
)
N
i
N
i
*
H
i
16·n bits
16·
n
bits
16 ·n bits
16·n bits
Figure 2.3: Round function.
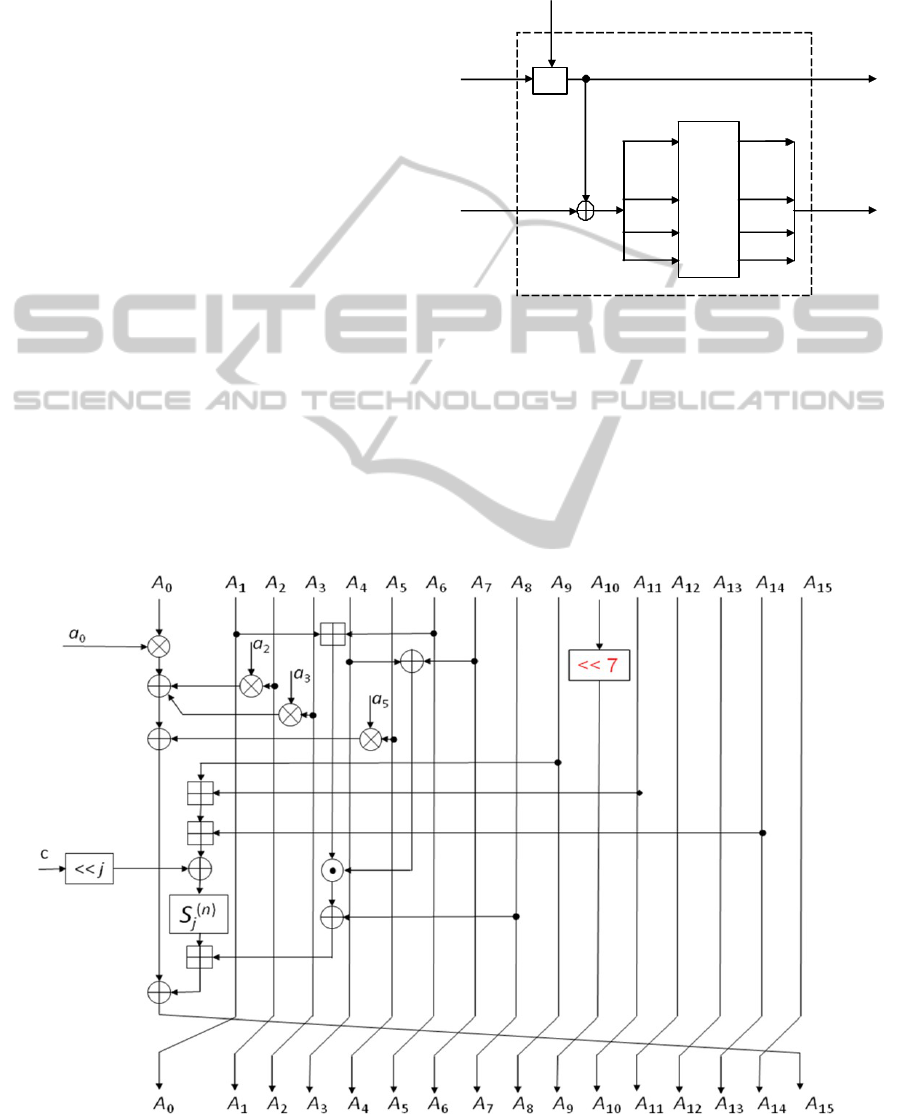
2.2.5 Step Function
The essential part of the round is the step function F
j
(Fig. 2.4). In each round the step function is
executed 16 times, for j=0, 1, …, 15.
Let GF[x]
n
be a set of polynomials over GF(2) of
the degree smaller than n. If w(x) ∈ GF[x]
n
then w(x)
= w
n–1
x
n–1
⊕ w
n–2
x
n–2
⊕ … ⊕ w
2
x
2
⊕ w
1
x ⊕ w
0
or
Figure 2.4: Step function F
j
.
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
190

simply w(x) = w
n–1
w
n–2
…w
2
w
1
w
0
, where w
r
∈ GF(2)
for r ∈ {0,1,…, n–1}. Let u(x), v(x), w(x) ∈ GF[x]
n
.
We define two operations on polynomials, addition
(⊕) and multiplication (⊗): u(x) = v(x) ⊕ w(x) ⇔ u
t
= v
t
⊕ w
t
, t = 1,2,…, n, and u(x) = v(x) ⊗ w(x) =
v(x)·w(x) mod R(x), where R(x) is a reduction
polynomial of degree n. In the construction of the
step function the multiplication of polynomials is
performed four times: a
0
⊗ A
0
, a
2
⊗ A
2
, a
3
⊗ A
3
,
and a
5
⊗ A
5
. The polynomials a
0
, a
2
, a
3
and a
5,
presented in hexadecimal form, are given in Table
2.1.
Table 2.1: Polynomials used in step function.
n R(x) Hexadecimal representation
16
x
16
⊕x
11
⊕x
10
⊕x
5
⊕1
10C21
32
x
32
⊕x
7
⊕x
6
⊕x
2
⊕1
1000000C5
64
x
64
⊕x
4
⊕x
3
⊕x⊕1
1000000000000001B
The reduction polynomials must be irreducible;
they are presented in Table 2.2.
Table 2.2: Reduction polynomials used in step function.
n a
0
a
2
a
3
a
5
16
89CB D949 0001 0001
32
AC2D
B263
0000
0110
0000
0001
0000
0001
64
EDC0
28B9
A461
A403
0000
2500
0000
0001
0000
0000
0000
0001
0000
0000
0000
0001
After performing multiplications of polynomials
a few additions modulo 2 (⊕) and additions modulo
2
n
(⊞) are done (Fig. 2.4). In each step the masking
constant c = 3236B539391FD066 (in hexadecimal
representation) is used. The particular value of c
depends on n and j, and is indicated by a window of
the length n sliding (cyclically, if necessary) from
left to right on bits of c. For example, if n = 16 and j
= 0 then c = 3236; if n = 32 and j = 31 then c =
391FD066; if n = 64 and j =5 then c =
6D6A72723FA0CD9 (cyclic rotation of c to the left
by 5 bits).
In each step a substitution S
j
(n)
depending (as the
masking constant c) on n and j is used. It consists of
four S-boxes S
0
, S
1
, S
2
and S
3
, each of dimension
16×16, working in such a way that for n = 16, S
j
(16)
= S
(j) mod 4
; for n = 32, S
j
(32)
= S
(j) mod 4
|| S
(j+1) mod 4
; and
for n = 64, S
j
(64)
= S
(j) mod 4
|| S
(j+1) mod 4
|| S
(j+2) mod 4
||
S
(j+3) mod 4
.
The multiplication modulo 2
n
+ 1 of n-bit
integers with the zero block corresponding to 2
n
is
denoted by ⊙ (Lai, 1991).
Table 2.3: Initial values of chaining variable.
n
H
0
= h
0
|| h
1
|| h
2
||…|| h
15
16
34D906D3E3E5298EAC26F9FD2AC5AD23
DB84B0576C82CCA52517CF6B88B0A90C
32
34D906D3E3E5298EAC26F9FD2AC5AD23
DB84B0576C82CCA52517CF6B88B0A90C
0BC69C6F64D4B2664579E064AE220A5A
3DA7C5451DA429EF2AE8BF289D0F01E5
64
34D906D3E3E5298EAC26F9FD2AC5AD23
DB84B0576C82CCA52517CF6B88B0A90C
0BC69C6F64D4B2664579E064AE220A5A
3DA7C5451DA429EF2AE8BF289D0F01E5
8C6595B7B088D0C74BB82BF3CFDE5AA1
AB808B7E7425BC9EFA101925CBB0D528
3FA76FCBDF7B50D776DE280C8E2EE8B1
69D154F43B096994FDF52B5F148CC134
The initial values H
0
= h
0
|| h
1
|| h
2
||…|| h
15
of
chaining variable (depended on n) are given in Table
2.3 (H
0
for n = 64 is obtained as the hexadecimal
form of consecutive 512 decimal places after the
decimal point of π broken up into groups of 32).
Before processing they must be assigned to A
0
|| A
1
||
A
2
||…|| A
15
in such a way that h
r
= A
r
, r = 0, 1,…, 15.
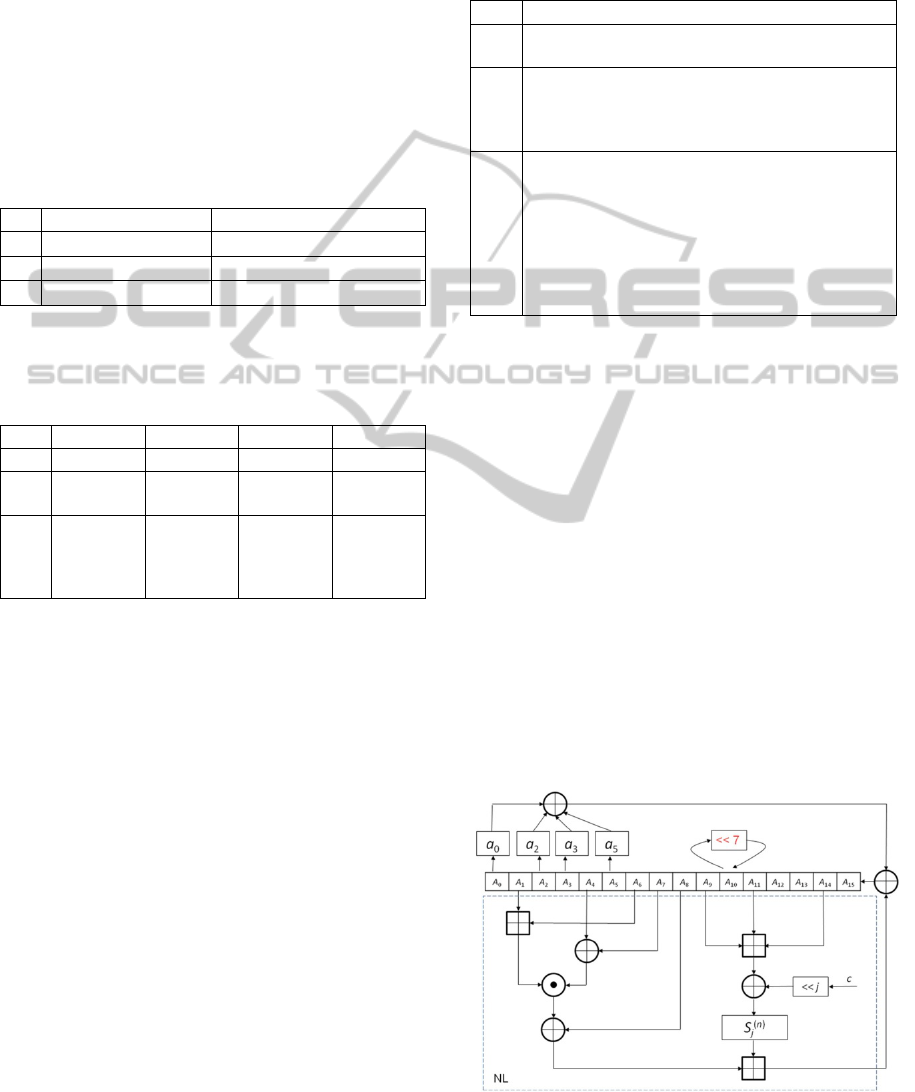
2.3 Security Considerations
The round function composed of 16 steps can be
represented in the equivalent form as a linear shift
register (FSR) over GF(2
n
) generating maximum
length sequences, additionally equipped with
nonlinear feedback NL, and clocked 16 times (Fig.
2.5). The corresponding approach dealing with the
use of feedback shift registers (over GF(2)) in the
construction of hash functions has been presented in
(Janicka-Lipska, 2004; Stokłosa, 1995).
Figure 2.5: Equivalent form of round function.
HaF - A New Family of Hash Functions
191

Maximum 16-stages linear feedback shift
register defined over GF(2
n
) generates the sequence
of period length T = 2
16n
– 1 (n = 16 or 32 or 64).
This period length is considerably decreased by the
nonlinear circuit (NL in Fig. 2.5). The processing of
every consecutive block M
i
of the formatted message
modifies initial content of the register and
consequently changes the period (meant as a
sequence of states) of the FSR. The same effect can
be observed when adding H
i
to the result of
processing the input by two rounds to obtain H
i+1
(Fig. 2.2). This implies that collisions exist but
finding them is difficult.
In order to achieve randomized hashing we use
the construction (see Fig. 2.2) in which the random
salt value s is added (mod 2) to each block M
i
(Biham, 2006).
The function defined by the nonlinear circuit is a
nonlinear 8n-argument function, n = 16 or 32 or 64.
For the function with such a number of arguments
(128, 256 and 512, respectively) it is difficult, from
the computational point of view, to perform the best
affine approximation attack (Rueppel, 1986). Time
needed for the attack is equal to time of the birthday
attack, i.e. O(2
8n
).
The sequence produced by the nonlinear circuit
is immune to correlation attack (Rueppel, 1986).
3 S-BOXES
3.1 Involutional S
Let
2
F
be the Galois field GF(2) and
n
2
F
be the n-
dimensional vector space over
2
F
. A substitution
operation or an n×n S-box (or S-box of the size n×n)
is a mapping:
nn
S
22
FF: →
(1)
where n is a fixed positive integer, n ≥ 2. An n-
argument Boolean function is a mapping:
22
FF: →
n
f
(2)
An S-box S can be decomposed into the
sequence S = (f
1
, f
2
, …, f
n
) of Boolean functions such
that S(x
1
, x
2
, …, x
n
) = (f
1
(x
1
, x
2
, …, x
n
), f
2
(x
1
, x
2
, …,
x
n
), …, f
n
(x
1
, x
2
, …, x
n
)). We say that the functions
f
1
, f
2
, …, f
n
are component functions of S.
In case of HaF’s S-box n = 16. HaF’s S-box
therefore is a function that takes 16 input bits and
outputs also 16 bits – it is a 16×16 S-box.
Additionally, it is generated in such a way that it is
its own inverse, i.e., S
−1
= S.
HaF’s S-box has been generated using the
multiplicative inverse procedure similar to AES
[Daemen 1999] with randomly chosen primitive
polynomial defining the Galois field. Nonlinearity of
this S-box is 32510 and its nonlinear degree is 15.
Sixteen Boolean functions that constitute this S-box
have nonlinearities equal to 32510 or 32512. The
degree of each function is equal to 15.
The 16×16 S-box can be stored as a table of
65536 word values. Index for this table is an input of
the S-box function, i.e., x
1
, x
2
, …, x
16
. Values stored
are S-box outputs (16 bits: f
1
(x
1
, x
2
, …, x
16
), f
2
(x
1
, x
2
,
…, x
16
), …, f
16
(x
1
, x
2
, …, x
16
)). To simplify the
description of S-box generation let’s consider a
smaller S-box of size 8×8. For presentation
convenience such S-box can be displayed as a 2-
dimensional table (Table 3.1). The input represented
as a two digit hexadecimal number HL is divided −
the low order digit (L) is on the horizontal axis and
the high order digit (H) is on the vertical axis. For
example, to see what is the S-box output at input 6F
take 6 on the vertical axis and F on the horizontal
axis. The S-box output is DA.
Table 3.1: Sample 8×8 S-box S.
L 0 1 2 3 4 5 6 7 8 9 A B C D E F
H ------------------------------------------------
0 | 9E BC C3 82 A2 7E 41 5A 51 36 3F AC E3 68 2D 2A
1 | EB 9B 1B 35 DC 1E 56 A5 B2 74 34 12 D5 64 15 DD
2 | B6 4B 8E FB CE E9 D9 A1 6E DB 0F 2C 2B 0E 91 F1
3 | 59 D7 3A F4 1A 13 09 50 A9 63 32 F5 C9 CC AD 0A
4 | 5B 06 E6 F7 47 BF BE 44 67 7B B7 21 AF 53 93 FF
5 | 37 08 AE 4D C4 D1 16 A4 D6 30 07 40 8B 9D BB 8C
6 | EF 81 A8 39 1D D4 7A 48 0D E2 CA B0 C7 DE 28 DA
7 | 97 D2 F2 84 19 B3 B9 87 A7 E4 66 49 95 99 05 A3
8 | EE 61 03 C2 73 F3 B8 77 E0 F8 9C 5C 5F BA 22 FA
9 | F0 2E FE 4E 98 7C D3 70 94 7D EA 11 8A 5D 00 EC
A | D8 27 04 7F 57 17 E5 78 62 38 AB AA 0B 3E 52 4C
B | 6B CB 18 75 C0 FD 20 4A 86 76 8D 5E 01 ED 46 45
C | B4 FC 83 02 54 D0 DF 6C CD 3C 6A B1 3D C8 24 E8
D | C5 55 71 96 65 1C 58 31 A0 26 6F 29 14 1F 6D C6
E | 88 F9 69 0C 79 A6 42 F6 CF 25 9A 10 9F BD 80 60
F | 90 2F 72 85 33 3B E7 43 89 E1 8F 23 C1 B5 92 4F
Cryptographically strong S-box should possess
some properties that are universally agreed upon
among researchers. Such S-box should be balanced,
highly nonlinear, have lowest maximum value in its
XOR profile (difference distribution table), have
complex algebraic description (especially it should
be of high degree). The above criteria are dictated by
linear and differential cryptanalysis and algebraic
attacks.
It is a well-known fact, that S-boxes generated
using finite field inversion mapping fulfill these
criteria to a very high extent. However, they are
susceptible to (theoretical) algebraic attacks. To
resist algebraic attacks multiplicative inverse
mapping used to construct an S-box is composed
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
192

with an additional invertible affine transformation.
This affine transformation does not affect the
nonlinearity of the S-box, its XOR profile nor its
algebraic degree. The best known example of such
an S-box is the S-box of AES. It has been publicly
known and it does not affect its security.
The algorithm used for generating the S-box for
the purpose of HaF function presented in this paper
uses similar method of generating S-boxes.
Additionally it takes into account results of some
recent studies (Fuller, 2002; Fuller, 2003) and
incorporates changes in the S-box generating
procedure to make it even more secure.
3.2 Generating Inverse Mapping
HaF S-box is based on so called inverse mapping
1−
→ xx
, where x
-1
denotes the multiplicative
inverse in a finite field GF(2
n
):
1
0 for 0
()
for 0
x
Sx
xx
-
=
=
¹
ì
ï
ï
í
ï
ï
î
(3)
As mentioned earlier, inversion mapping can be
used to generate cryptographically strong S-boxes.
For any prime integer p and any integer n (n =
1,2,…), there is a unique field with p
n
elements,
denoted GF(p
n
). In cryptography p almost always
takes the value of 2. To generate an inverse mapping
in GF(2
n
) we need an irreducible polynomial that
defines a Galois field and another polynomial that
would be a so called generator (see below). A
polynomial is said to be irreducible if it cannot be
factored into nontrivial polynomials over the same
field. The n-bit elements of the Galois field are
treated as polynomials with coefficients in F
2
. For
example, in case of AES, where S-box is of size 8×8
we operate mostly on bytes represented as
b
7
b
6
b
5
b
4
b
3
b
2
b
1
b
0
which corresponds to the following
polynomial:
b
7
x
7
+ b
6
x
6
+ b
5
x
5
+ b
4
x
4
+
b
3
x
3
+ b
2
x
2
+ b
1
x + b
0
(4)
where b
i
∈ {0,1}.
An irreducible polynomial mentioned above is
used to calculate a multiplication in GF(2
n
). When
two polynomials are multiplied the resulting product
is a polynomial of degree at most 2(n–1) – too much
to fit into n-bit data word that represents
polynomials in GF(2
n
), so the intermediate product
of this multiplication is divided by the irreducible
polynomial and the remainder of this division is the
result of the multiplication. For GF(2
n
) an
irreducible polynomial should be of degree n. For
example, in AES (with GF(2
8
)) an irreducible
polynomial selected for construction of the S-box is
11B (in hexadecimal notation).
A generator in Galois field is a polynomial
whose successive powers take on every element
except zero. Which polynomials are generators in a
particular Galois field depends on the irreducible
polynomial selected. So say polynomial 03 is a
generator in GF(2
8
) with irreducible polynomial 11B
(as in AES), but it is not a generator in GF(2
8
) with
irreducible polynomial 1BD, for which the generator
is for example 07.
For n = 8 the nonlinearity of this mapping treated
as an S-box is 112. For n = 16 it is 32512. In general
case, the nonlinearity of such a mapping is 2
n–1
–
2
n/2
.
However, such an S-box would always have 0
and 1 as first two entries. This is because for x = 0,
x
-1
= 0 and for x = 1, x
-1
= 1. These would be
undesirable fixed points of an S-box. We remove
them in the next step.
3.3 Affine Transformation
To avoid algebraic attacks (given multiplicative
inversion's simple algebraic form) every element of
the table of multiplicative inverses is changed using
an affine transformation. Such transformation has to
be a full permutation, so every element is changed
and all possible elements are represented as the
result of a change, so that no two different bytes are
changed to the same byte. After applying this
transformation the table is still a bijective mapping
which is inversible and that is a prerequisite for most
applications of S-boxes. In case of AES cipher this
affine transformation is given by the following
equation:
iii
iiii
cbb
bbbb
⊕⊕
⊕⊕⊕=
++
++
8mod)7(8mod)6(
8mod)5(8mod)4(
'
(5)
where c is an 8-bit constant (in case of AES it equals
63 in hexadecimal notation). i is the bit position.
This transformation can also be represented as
matrix multiplication:
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
'
10001111
'
11000111
'
11100011
'
11110001
'
11111000
'
01111100
'
00111110
'
00011111
bb
bb
bb
bb
bb
bb
bb
bb
=
é
ùéù
é
ù
êú êú
êú
êú êú
êú
êú êú
êú
êú êú
êú
êú êú
êú
êú êú
êú
êú êú
êú
êú êú
êú
êú ê
êú
êú ê
êú
êú ê
êú
êú ê
êú
êú ê
êú
êú ê
êú
ê
ú
ê
úê
ë
û
ë
ûëû
1
1
0
0
0
1
1
0
+
éù
êú
êú
êú
êú
êú
êú
êú
êú
ú
êú
ú
êú
ú
êú
ú
êú
ú
êú
ú
êú
êú
ú
ëû
(6)
HaF - A New Family of Hash Functions
193

The algorithm used for generating S-box S of
HaF function in this paper uses the same
transformation, however adopted for 16×16 S-box
size and with the constant part of this transformation
(namely c
i
) taken at random so that resulting S-box
does not have fixed points (such that S(x) = x).
Particularly the two fixed points mentioned in the
previous paragraph (0 and 1) are removed by this
transformation.
3.4 Removing Cycles
One of the requirements for HaF S-box is the
absence of cycles. Cycle is such a sequence of S-box
values S
0
, S
1
, … S
k-1
where S
(i+1) mod k
= S(S
i
). HaF S-
box should have only one such cycle containing all
the values of the S-box (a cycle for which k = 2
n
).
The affine transformation described in previous
paragraph changes number of cycles in an S-box,
without changing its nonlinear properties. Note that
fixed points are also short cycles where k = 1.
Cycles are removed in a procedure with two
steps. First step is actually the aforementioned affine
transformation. It is applied repeatedly with a
random value of c until the S-box with only 2 cycles
is found. This might not always be possible. In such
a case a new S-box has to be generated with another
randomly chosen primitive polynomial using the
inverse mapping as described earlier.
When 2-cycle S-box is found we move on to the
next step, which is performed together with
removing the affine equivalence.
3.5 Removing Affine Equivalence
According to (Fuller, 2002; Fuller, 2003), S-boxes
based on multiplicative inverse in a finite field have
such a peculiar property that all component
functions of the S-box are from the same affine
equivalence class (all the output functions of the S-
box can be mapped onto one another using affine
transformations). HaF’s S-box has been processed to
remove this linear redundancy, so that all Boolean
functions are now from different affine equivalence
classes, while still maintaining exceptionally high
nonlinearity of the inverse mapping. The proposed
S-box has the maximum XOR difference
distribution table value of 6, which is extremely
good.
Removing this linear redundancy in 2-cycle S-
box is carried out in such a way that it will at the
same time reduce the number of cycles to only 1. It
is done by choosing randomly two S-box entries x
and y, each belonging to another cycle, and
rearranging S-box entries in such a way, that both
cycles are joined into one.
After such change a test for linear redundancy is
performed. If affine equivalence is still present
(between any component functions) the change is
reversed and different S-box entries are randomly
selected and tested – this procedure is carried out
until S-box without linear redundancy is found. If
such an S-box cannot be found, we need to generate
another S-box with inverse mapping.
Many properties of Boolean functions covered
by various cryptographic criteria (such as algebraic
degree and nonlinearity) remain unchanged by affine
transformations. Absolute values of Walsh transform
as well as autocorrelation function are only
rearranged by affine transformations. The frequency
distribution of the absolute values in these
transforms is invariant under such affine
transformations. To prove that two functions are
from different equivalence classes it is therefore
sufficient to show that their respective Walsh
transform or autocorrelation function frequency
distribution is different.
4 REFERENCE
IMPLEMENTATIONS OF
HaF-256
HaF-256 algorithm was implemented using of C++
language and Microsoft Visual Studio 2008
environment. Two reference implementations were
separately developed and tested using of reference
data. The results produced by the implementations
were compared with each other in order to verify
algorithm implementation accuracy.
To evaluate performance a 20 MB text file was
processed and the time was measured. Several
options were considered. For Windows (64-bit
Windows 7) two compilers were used: native Visual
Studio C++ compiler and Intel C++ compiler. The
code was generated for 32-bit and 64-bit platforms.
Table 4.1: Results of performance measurements.
System Platform Compiler
Performance
[MB/s]
Windows 7 32-bit VS2008 1.29
Windows 7 64-bit VS2008 1.60
Windows 7 32-bit Intel 2.99
Windows 7 64-bit Intel 3.13
Linux 32-bit GCC 0.74
Linux 32-bit GCC -O 1.17
Linux 32-bit GCC -O2 1.36
Linux 32-bit GCC -O3 2.33
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
194

Linux (Fedora 9) GCC compiler was used
without and with optimization. The code was
generated for 32-bit platform only. PC machine with
2.2 GHz Athlon-64 processor was used as a testing
platform. The results are presented in Table 4.1.
As shown in Table 4.1, the best result was
obtained using Intel compiler. For 64-bit platform
the performance was about 4.7% better than for 32-
bit platform. Bigger improvement may be expected
for HaF-1024 implemented using 64-bit variables.
For the sake of comparison we measured
performance of one of the NIST SHA 3 competition
finalists – BLAKE hash function [Aumasson, 2011],
using the same computer. BLAKE algorithm is very
simple and does not use S-boxes. Results are
presented in Table 4.2. As we can see, BLAKE
significantly outperforms HaF. But in some
applications it does not matter. For example, it takes
0.03 s to compute hash for a 100 kB message using
HaF-256, whereas 0.0005 s is required for BLAKE-
256.
Table 4.2: BLAKE-256 performance.
Compiler 32-bit version 64-bit version
VS2008 175 MB/sec 256 MB/s
Intel C++ Compiler 204 MB/sec 240 MB/s
5 CONCLUDING REMARKS
Most cryptographic hash functions designers focus
on high processing speed. Therefore relatively
simple algorithms are preferred. Implementations of
these algorithms may be vulnerable to fault attack
and side channel attack.
In HaF hash functions family processing scheme
is more elaborated and we use relatively big 16 × 16
S-boxes. It leads to more complex implementation.
We expect it to give greater robustness against
fault attack and side channel attack.
We currently experiment with fault attacks on
HaF implementation, so it should be possible to
verify what are the advantages of this approach.
ACKNOWLEDGEMENTS
This work was supported by the Polish Ministry of
Science and Higher Education as a 2010–2013
research project.
REFERENCES
Biham E., Dunkelman O., 2007. A framework for iterative
hash functions - HAIFA, NIST 2nd Hash Function
Workshop, Santa Barbara, August 2006; also:
Cryptology ePrint Archive: Report 2007/278,
http://eprint.iacr.org/2007/278.
Daemen J., Rijmen V., 1999. AES Proposal: Rijndael,
AES’99, http://csrc.nist.gov/CryptoToolkit/aes/
rijndael/1999
Fuller J., Millan W., 2002. On Linear Redundancy in the
AES S-Box, http://eprint.iacr.org/2002/111.
Fuller J., Millan W., 2003. On Linear Redundancy in S-
Boxes, FSE 2003, LNCS 2887, 74–86, Springer 2003.
Janicka-Lipska I., Stokłosa J., 2004. Boolean feedback
functions for full-length nonlinear shift registers.
Journal of Telecommunications and Information
Technology, 2004, 5, 28−30.
Lai X., Massey J. L., 1991. A proposal for a new block
encryption standard. Damgård I. B. (ed.), Advances in
Cryptology – EUROCRYPT ’90. LNCS 473, Springer,
Berlin, 1991, 389–404.
Menezes A. J., van Oorschot P.C., Vanstone S. A., 1997.
Handbook of Applied Cryptography. CRC Press, Boca
Raton, FL,1997.
Rueppel R. A., 1986. Analysis and Design of Stream
Ciphers. Springer, Berlin, 1986.
Stokłosa J., 1995. Integrity of data: FSR-hash. Bubnicki
Z. (ed.), Proceedings of the 12th International
Conference on Systems Science. Oficyna Wydawnicza
Politechniki Wrocławskiej, Wrocław, 1995, 120–125.
Aumasson J.P., Henzen L., Meier W., C.-W. Phan R. C.-
W, 2011. SHA-3 proposal BLAKE. Submission to
NIST, version 1.4, January 11, 2011,
Regenscheid A., Perlner R., Cjen Chang S., Kelsey J.,
Nandi M., Paul S., 2009. Status Report on the First
Round of the SHA-3 Cryptographic Hash Algorithm
Competition, Technical Report 7620 NIST (September
2009), http://csrc.nist.gov/groups/ST/hash/sha-3/
Round1/documents/sha3_NISTIR7620.pdf
HaF - A New Family of Hash Functions
195