TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC

LIKELIHOOD COMPUTATIONS

Fernando Izquierdo-Carrasco

, Julien Gagneur

and Alexandros Stamatakis

The Exelixis Lab, Scientiﬁc Computing Group, Heidelberg Institute for Theoretical Studies

Schloss-Wolfsbrunnenweg 35, D-69118 Heidelberg, Germany

European Molecular Biology Laboratory, Meyerhofstr. 1, 69117 Heidelberg, Germany

Keywords:

Memory versus runtime trade-offs, Phylogenetic likelihood function, RAxML.

Abstract:

The revolution in wet-lab sequencing techniques that has given rise to a plethora of whole-genome or whole-

transcriptome sequencing projects, often targeting 50 up to 1000 species, poses new challenges for efﬁciently

computing the phylogenetic likelihood function both for phylogenetic inference and statistical post-analysis

purposes. The phylogenetic likelihood function as deployed in maximum likelihood and Bayesian inference

programs consumes the vast majority of computational resources, that is, memory and CPU time. Here, we

introduce and implement a novel, general, and versatile concept to trade additional computations for memory

consumption in the likelihood function which exhibits a surprisingly small impact on overall execution times.

When trading 50% of the required RAM for additional computations, the average execution time increase

because of additional computations amounts to only 15%. We demonstrate that, for a phylogeny with n

species only log(n) + 2 memory space is required for computing the likelihood. This is a promising result

given the exponential growth of molecular datasets.

1 INTRODUCTION

The rapid accumulation of molecular sequence data

that is driven by novel wet-lab techniques poses new

challenges regarding the design of programs for phy-

logenetic inference that rely on computing the Phylo-

genetic Likelihood Function (PLF) for phylogenetic

inference or statistical post-analysis. For instance, we

are currently involved in two large-scale sequencing

efforts aimed at obtaining, whole genome data for

approximately 150 species and whole transcriptome

data for approximately 1000 species

In all popular Maximum Likelihood (ML) and

Bayesian phylogenetic inference programs, the PLF

dominates both, the overall execution time as well

as the memory requirements by typically 85% -

95% (Stamatakis and Ott, 2008).

Based on our interactions with the RAxML user

community, we ﬁnd that memory shortages are in-

creasingly becoming a problem and represent the

main limiting factor for large-scale phylogenetic anal-

yses, especially at the Genome level. At the same

time, the amount of available genomic data is growing

Because of non-disclosure agreements we can not pro-

vide further details about these projects at present.

at a faster pace than RAM (Random Access Mem-

ory) sizes and RAM access speeds. For instance, to

compute the likelihood on a simulated DNA align-

ment with 1,481 species and 20,000,000 sites (cor-

responding roughly to the 20,000 genes in the hu-

man genome) on a single tree topology under a simple

statistical model of nucleotide substitution within 48

hours, 1TB of memory and a total of 672 cores are

required.

We have already assessed some potential solutions

to this problem in previous work:

1. Single Precision. Deploying single precision

arithmetics that can reduce memory requirements

by 50% but can potentially induce numerical in-

stability, especially on datasets with more than

1000 taxa (Berger and Stamatakis, 2010).

2. Gappy Alignments. Novel algorithmic solutions

which rely on dataset-speciﬁc properties, that is,

their efﬁciency/applicability depends on the spe-

ciﬁc properties of the Multiple Sequence Align-

ment (MSA) that is used as input (Stamatakis and

Alachiotis, 2010). In particular, these algorithmic

approaches do not work on multi-gene datasets

that do not contain enough missing data on a per-

gene basis, that is, when gene sequences for a

Izquierdo-Carrasco F., Gagneur J. and Stamatakis A..

TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC LIKELIHOOD COMPUTATIONS.

DOI: 10.5220/0003765600860095

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 86-95

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

certain number of taxa under study are not avail-

able. In other words, these approaches are not ap-

plicable to emerging, dense whole-genome MSAs

without missing data.

3. Out-Of-Core. We recently introduced a gen-

erally applicable method for saving memory,

that does not rely on MSA-speciﬁc characteris-

tics. We evaluated an out-of-core (frequently

also called external memory algorithm) approach

that reduces RAM requirements by moving data

back and forth between the RAM and the

disk (Izquierdo-Carrasco and Stamatakis, 2011).

However, the increase of at least one order of

magnitude in overall execution times because of

slow read/write operations to/from disk does not

yield this approach practical, even when a high

performance parallel ﬁle system is used.

Here, we introduce a novel and signiﬁcantly more

efﬁcient method that is based on trading computations

(runningtime) for memory. The method is completely

independent from the MSA structure and is therefore

particularly useful for reducing RAM requirements

of “dense” whole-genome alignments. Moreover, it

can be combined with the single precision and gappy

alignment memory saving approaches (see above) to

yield even further savings. When reducing the amount

of available RAM to 50% of the total RAM required

for computing the likelihood on a tree for a given

MSA, we obtain a respective slowdown (because of

additional (re-)computations) of only 15%. This rep-

resents a relatively small run-time increase that most

end-users will not even notice. On the other hand,

users will notice when their analyses crash because

they have run out of RAM or the OS (operating sys-

tem) starts paging.

The remainder of this paper is organized as fol-

lows: We brieﬂy review related work in Section 2.

In Section 3 we describe the underlying idea for

the memory saving approach, demonstrate that only

log(n) + 2 vectors are required, and introduce two

vector replacement strategies. In Section 4 we de-

scribe the experimentalsetup and providecorrespond-

ing results. We conclude and discuss directions of fu-

ture work in Section 5.

2 RELATED WORK

One common approach for reducing memory require-

ments are out-of-core algorithms. These are specif-

ically designed to minimize the I/O overhead via

explicit, application-speciﬁc, data placement control

and movement. Out-of-core algorithms mostly aim at

optimizing data movement between disk and RAM.

A comprehensive review of work on out-of-core al-

gorithms can be found in (Vitter, 2008). In phylo-

genetics, out-of-core algorithms have been applied to

Neighbor-Joining (Wheeler, 2009; Martin Simonsen

and Pedersen, 2010). Moreover, we recently intro-

duced a generic out-of-core implementation for PLF

computations (Izquierdo-Carrasco and Stamatakis,

2011). As already mentioned, the performance of our

out-of-core implementation was rather disappoint-

ing and is therefore not applicable to likelihood-

based inference on dense whole-genome alignments.

Nonetheless, our approach was signiﬁcantly more ef-

ﬁcient than the paging strategy of the OS.

The term time-memory trade-off engineering

refers to situations/approaches where memory re-

quirements/utilization is reduced at the cost of ad-

ditional (re-)computations, that is, at the expense of

increased run time. This trade-off engineering ap-

proach has been applied in diverse ﬁelds such as lan-

guage recognition (Dri and Galil, 1984), cryptogra-

phy (Barkan et al., 2006), and packet scheduling (Xu

and Lipton, 2005).

We are not aware of any applications of or exper-

iments with time-memory trade-off engineering ap-

proaches in the ﬁeld of computational phylogenetics.

3 RECOMPUTATION OF

ANCESTRAL PROBABILITY

VECTORS

3.1 PLF Memory Requirements

A detailed discussion on PLF Memory requirements

is provided in (Izquierdo-Carrasco and Stamatakis,

2011). We include a part of this discussion, that is

also relevant for the work presented here. The PLF

is deﬁned on unrooted binary trees. The n extant

species/organisms of the MSA under study are lo-

cated at the tips of the tree, whereas the n − 2 in-

ner nodes represent extinct common ancestors. The

molecular sequence data in the MSA that has a length

of s sites (alignment columns) is located at the tips of

the tree. The memory requirements for storing those

n tip vectors of length s is not problematic, because

one 32-bit integer is sufﬁcient to store, for instance, 8

nucleotides when ambiguous DNA character encod-

ing (requiring 4 bits to store one nucleotide) is used.

Hence, for the aforementioned large dataset (1,481

species, 20,000,000 sites) only 13GB are required to

store the actual sequence data compared to 1 TB for

storing ancestral probability vectors.

TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC LIKELIHOOD COMPUTATIONS

Hence, the memory requirements of the PLF are

dominated by the space for storing the ancestral prob-

ability vectors that are located at the ancestral (inner)

nodes of the tree. Depending on the PLF implemen-

tation, at least one such vector (a total of n− 2) will

need to be stored per ancestral node. For each align-

ment site i,i = 1...s, an ancestral probability vector

needs to hold the data for the probability of observing

A, C, G

. Thus, under double precision arith-

metics and for DNA data a total of (n− 2)·8·4·s bytes

is required for the most simple statistical model of nu-

cleotide substitution. When the less simplistic, stan-

dard Γ model of rate heterogeneity (Yang, 1994) with

4 discrete rates is deployed, this number increases by

a factor of four ((n− 2) · 8 · 16 · s), since we need to

store 16 probabilities for each alignment site i. Fur-

thermore, if protein data is used (that has 20 instead of

4 states) in conjunction with the Γ model of rate het-

erogeneity, the memory requirements for storing an-

cestral probability vectors increase to (n− 2)· 8· 80· s

bytes.

To obtain the likelihood of a given, ﬁxed tree, the

PLF performs a post-order tree traversal that starts at

a virtual root. Such a virtual root can be placed ar-

bitrarily into any branch of the unrooted tree without

changing the overall likelihood of the tree. By means

of the post-order tree traversal, the ancestral probabil-

ity vectors are computed bottom-up from the leaves

toward the virtual root.

For a more detailed description of PLF computa-

tions and efﬁcient PLF implementations please refer

to (Stamatakis, 2011). For understanding the memory

access pattern during the post-order traversal, let us

consider equation (Felsenstein, 1981) of the Felsen-

stein pruning algorithm.

This equation computes the ancestral probability

vector entry

(p)

for observing the nucleotide

at site

i of a parent node p, with two child nodes l and r given

the respective branch lengths b

and b

, the corre-

sponding transition probability matrices P(b

), P(b

and the probability vectors of the children

(l)

(r)

(p)

(i) =



∑

S=A

)

(l)

(i)



∑

S=A

)

(r)

(i)



(1)

In order to compute L

(p)

(i), we do not necessarily

need to immediately have available in memory vec-

tors L

(l)

(i) and L

(r)

(i), since they can be obtained by a

recursive descent (a post-order subtree traversal) into

the subtrees rooted at l and r using the above equation.

In other words, if we do not have enough memory

available, we can recursively re-compute the values

of L

(l)

and L

(r)

. Note that, the recursion terminates

when we reach the tips (leaves) of the tree and that

memory requirements for storing tip vectors are neg-

ligible compared to ancestral vectors (see above).

If not all ancestral probability vectors ﬁt in RAM,

the required vectors for the operation at hand can still

be obtained by conducting some additional compu-

tations for obtaining them by applying equation 1.

We observe that, when both L

(l)

(i) and L

(r)

(i) have

been used (consumed) for calculating L

(p)

(i), the two

child vectors are not required any more. That is, those

two vectors can be omitted/dropped from RAM or be

overwritten in RAM to save space. Therefore, the

likelihood of a tree can be computed without storing

all n − 2 ancestral vectors. Instead, a smaller amount

of space for only storing x < (n − 2) vectors can be

used. Those x vectors can then dynamically be as-

signed to a subset (varying over time) of the n − 2

inner nodes. This gives rise to the following question:

Given a MSA with n taxa, what is the minimum num-

ber of inner vectors x

min

that must reside in memory

to be able to compute the likelihood on any unrooted

binary tree topology with n taxa?

Due to the post-order traversal of the binary tree

topology, some ancestral vectors need to be stored

as intermediate results. Consider an ancestral node

p that has two subtrees rooted at child nodes l and r

with identical subtree depth. When the computations

on the ﬁrst subtree for obtaining L

(l)

have been com-

pleted, this vector needs to be kept in memory until

the ancestral probability vector L

(r)

has been calcu-

lated to be able to compute L

(p)

3 4

virtual root

Figure 1: A balanced subtree, where the vector of inner

node 1 is oriented in the direction of the virtual root. In

order to compute the likelihood of vector 1, the bold vec-

tors must be held in memory. The transparent vectors may

reside in memory but are not required to.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

In the following section 3.2, we demonstrate that

the minimum number of ancestral vectors x

min

(n) that

must reside in RAM to be able to compute the likeli-

hood of a tree with n taxa is log

(n) + 2. For obtain-

ing this lower memory bound, we consider the worst

case tree shape, that is, a perfectly balanced unrooted

binary tree with the virtual root placed into the inner-

most branch.

Figure 1, where we ﬁrst descended into the left

subtree, depicts this worst case scenario for n = 4.

The probability vectors will be written in the follow-

ing order:

3, 4, 2, 6, 7, 5, 1

. Figure 1 shows

the number of vectors required in memory (log

(4) +

2 = 4) at the point of time where vector 5 needs to be

computed. At any other point of time during the post-

order traversal, holding 3 vectors in RAM is sufﬁcient

to successfully proceed with the computations.

3.2 Minimum Memory Requirements

The underlying idea of our approach is to reduce the

total number of ancestral probability vectors residing

in RAM at any given point of time. Let PLF be the

likelihood function (see Equation 1), which —for the

sake of simplifying our notation— can be computed

at a tip (essentially at zero computational cost) or an

inner node given the ancestral probability vectors of

its two child nodes. The PLF always returns an an-

cestral probability vector as result.

As a pre-processing step, we compute the num-

ber of descendants (size of the respective subtree) for

each inner node. This can be implemented via a sin-

gle post-order tree traversal. The memory required

for storing the number of descendants as integers at

each node is negligible compared to required proba-

bility vector space. Given this information, the binary

tree data structure can be re-ordered such that, for ev-

ery node p, the left child node l contains the larger

number of descendants and the right child node r con-

tains the smaller number of descendants. We can now

compute the PLF of the tree by invoking the follow-

ing recursive procedure f at the virtual root p of the

tree:

proc f(p) ≡

if isALeaf(p) then return(PLF(p)) ﬁ;

:= f(p.l); Step 1

:= f(p.r); Step 2

return(PLF(v

)) Step 3

During this computation, the maximum number of

probabilityvectors x

min

(n) that need to reside in mem-

ory for any tree with n leaves is log

(n) + 2. This up-

per bound is required if and only if the binary tree is

balanced.

Proof. We demonstrate the above theorem by re-

cursion. x

min

(1) = 1, since for a tree with a sin-

gle node, only the sequence data (a single proba-

bility vector) need to be stored. Now assume that

min

(n− 1) = log

(n− 1) + 2 and consider a tree with

n leaves. We execute all steps of f(p), where p is

the root, and keep track of the number of probability

vectors that are stored simultaneously in RAM:

• Step 1. Computing f(p.l) requires storing at

most x

min

(n − 1) probability vectors simultane-

ously which is strictly less than log

(n)+ 2. Once

f(p.l) has been computed only the result vector is

stored (i.e., only one single probability vector).

• Step 2. Because the subtree size of the right de-

scendant of the root p.r must be ≤ n/2, this com-

putation needs to simultaneously store at most

log

(n/2) + 2 = log

(n) + 1 probability vectors.

Here, we need to add the number of probability

vectors that required to be maintained in RAM af-

ter completion of Step 1. Thus, overall, Step 2

needs to simultaneously hold at most log

(n) + 2

probability vectors in RAM. Once the results of

f(p.l) and f(p.r) have been computed we are left

with two probability vectors v

that need to re-

side in memory.

• Step 3. This step requires 3 probability vectors to

be stored at the same time, namely, v

, v

, and the

vector to store the result of PLF(v

). Note that,

to obtain the overall likelihood of the tree (a single

numerical value), we need to apply a function g()

to the single result vector returned by f(), that is,

g( f(p)). Function g() simply uses the data in the

result vector to calculate the likelihood score over

all root vector entries.

Hence the peak in memory usage is reached dur-

ing Step 2 and its upper bound is log

(n) + 2. More-

over, this upper bound is reached if and only if the

number of descendants in the respective left and right

subtrees is identical for all nodes, that is, for a bal-

anced tree.

3.3 Basic Implementation

While holding log

(n) + 2 vectors in RAM provides

sufﬁcient space for computing the PLF, this will in-

duce a signiﬁcant run-time increase (due to recom-

putations) compared to holding n vectors in memory.

In practice, we need to analyze and determine a rea-

sonable run-time versus RAM trade-off as well as an

appropriate vector replacement/overwriting strategy.

For instance, in the RAxML or MrBayes PLF im-

plementations, some ancestral vectors (depending on

their location in the tree) can be recomputed faster

TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC LIKELIHOOD COMPUTATIONS

than others. In particular, cases where the left and/or

right child vectors are tip sequences can be handled

more efﬁciently. For instance, an observed nucleotide

at a tip sequence corresponds to a simple probability

vector of the form [P(A) := 1.0, P(C) := 0.0,P(G) :=

0.0,P(T) := 0.0]. This property of tip vectors can be

used for saving computations in equation 1.

Also, typical topological search operators for ﬁnd-

ing/constructing a tree topology with an improved

likelihood score such as SPR (Subtree Pruning and

Re-grafting), NNI (Nearest Neighbor Interchange) or

TBR (Tree Bisection and Reconnection) only apply

local changes to the tree topology. In other words,

the majority of the ancestral probability vectors is not

affected by the topological change and does there-

fore not need to be recomputed/updated with respect

to the locally altered tree topology via a full post-

order tree traversal. Therefore, if all ancestral vec-

tors reside in RAM, only a very small part of the

tree needs to be (re-)traversed after a SPR move, for

instance. All standard ML-based programs such as

GARLI (Zwickl, 2006), PHYML 3.0 (Guindon et al.,

2010), and RAxML (Stamatakis, 2006) deploy search

strategies that typically require updating only a small

fraction of probability vectors in the vicinity of the

topological change.

Therefore, devising an appropriate strategy (see

Section 3.4) for deciding which vectors shall remain

in RAM and which can be discarded (because they

can be recomputed at a lower computational cost)

can have a substantial impact on the induced run

time overhead when holding, for instance, x := n/2

vectors in RAM. In the following, we will outline

how to compute the PLF and conduct SPR-based tree

searches with x < n vectors in RAM.

Let n be the number of species, n− 2 the number

of ancestral probability vectors, and x the number of

available slots in memory, where log

(n) + 2 ≤ x <

n (i.e., n − x vectors are not stored, but recomputed

on demand). Let w be the number of bytes required

for storing an ancestral probability vector (all vectors

have the same size). Our implementation will only

allocate x· w bytes, rather than n· w. We henceforth

use the term slot to denote a RAM segment of w bytes

that can hold an ancestral probability vector.

We deﬁne the following C data structure (details

omitted) to keep track of the vector-to-slot mapping

of all ancestral vectors and for implementing replace-

ment strategies:

typedef struct

{

int numVectors;

size_t width;

double **tmpvectors;

int *iVector;

int *iNode;

int *unpinnable;

boolean allSlotsBusy;

unpin_strategy strategy;

}recompVectors;

The array

tmpvectors

is a list of pointers to

a set of slots (i.e., starting addresses of allocated

RAM memory) of size

numVectors

(x) and width

numVector

(w). The array

iVector

has length x and

is indexed by the slot id. Each entry holds the node

id of the ancestral vector that is currently stored in the

indexed slot. If the slot is free, the value is set to a

dedicated

SLOT_UNUSED

code. The array

iNode

has

length n− 2 and is indexed using the unique node ids

of all ancestral vectors in the tree. When the corre-

sponding vector resides in RAM, its array entry holds

the corresponding slot id. If the vector does not re-

side in RAM the array entry is set to the special code

NODE_UNPINNED

. Henceforth, we denote the avail-

ability/unavailability of an ancestral vector in RAM

pinned/unpinned

The array

unpinnable

tracks

which slots are available for unpinning, that is, which

slots that currently hold an ancestral vector can be

overwritten, if required.

The set of ancestral vectors that are stored in the

memory slots changes dynamically during the com-

putation of the PLF (i.e., during full tree traversals

and tree searches). The pattern of dynamic change in

the slot vector also depends on the selected recom-

putation/replacement strategy. For each PLF invoca-

tion, be it for evaluating a SPR move or completely

re-traversing the tree, the above data structure is up-

dated accordingly to ensure consistency.

Whenever we need to compute a local tree traver-

sal (following the application of an SPR move) to

compute the likelihood of the altered tree topology,

we initially just compute the traversal order which is

part of the standard RAxML implementation. The

traversal order is essentially a list that stores in which

order ancestral probability vectors need to be com-

puted. In other words, the traversal descriptor de-

scribes the partial or full post-order tree traversal re-

quired to correctly compute the likelihood of a tree.

For using x < n vectors, we introduce a so-called

traversal order check, which extends the traversal

steps (the traversal list) that assume that all n vec-

tors reside in RAM. By this traversal order extension,

we guarantee that all missing vectors (not residing in

RAM) will be recomputed as needed. The effect of

reducing the number of vectors residing in RAM is

that, traversal lists become longer, that is, more nodes

are visited and thereby run time increases. When the

traversal is initiated, all vectors in the traversal list

that already reside in RAM (they are pinned to a slot)

are protected (marked as

unpinnable

) such that, they

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

will not be overwritten by intermediate vectors of the

recomputation steps.

If an ancestral vector slot needs to be writ-

ten/stored by the traversal, there are three cases:

1. The vector resides in a slot (already in memory).

We can just read and/or write to this slot.

2. The vector is not pinned, but there exists a free

slot, which is then pinned to this vector.

3. The vector is not pinned and there is no free slot

available. A residing vector must be replaced and

the corresponding slot needs to be pinned to the

required vector.

Since the traversal only visits each vector at most

once, the corresponding children of this vector can be

unpinned once it has been written to memory. Instead

of unpinning them directly, they are merely marked

for unpinning. The real overwrite only takes place

if the slot is selected by the replacement strategy for

storing another vector. Otherwise, the slot will store

the values of the current vector for as long as possible

for potential future re-use.

3.4 Replacement Strategies

In analogy to the replacement strategies discussed in

the out-of-core implementation (Izquierdo-Carrasco

and Stamatakis, 2011), there are numerous ap-

proaches for deciding which memory slot should be

overwritten by a new ancestral vector that does cur-

rently not reside in RAM. We implement and analyze

the following two replacement strategies.

Random. A random slot not ﬂagged as pinned is se-

lected. The random strategy is a na¨ıve approach

with minimal overhead and is used as baseline for

performance comparisons.

MRC. Minimum Recomputation Cost. The slot with

minimum subtree size (see below) and not ﬂagged

as pinned is selected.

The MRC strategy entails a slight overhead for

keeping track of which vectors will be most expen-

sive to recompute and should therefore be kept in

RAM for as long as possible. Consider an unrooted

binary tree T with n tips. Each inner node i in an

unrooted binary tree with n taxa can be regarded as

a trifurcation that deﬁnes three subtrees T

i,a

, T

i,b

, and

i,c

corresponding to the three outgoing branches a,b,

and c. Given a subtree T

i,x

, we deﬁne its subtree

size sts(T

i,x

) as the number of tips beneath inner node

i in the direction of the outgoing branch x. Thus,

sts(T

i,a

) + sts(T

i,b

) + sts(T

i,c

) = n holds for any in-

ner node i in an unrooted binary tree with n taxa/tips.

When conducting likelihood computations, the tree is

always rooted by a virtual root. Hence, if the virtual

root is located in the direction of branch c the rele-

vant subtree size with respect to recomputation cost

at inner node i is sts(T

rooted

) := sts(T

i,a

) + sts(T

i,b

We use this rooted subtree size sts(T

rooted

) to deter-

mine the recomputation cost for each ancestral vector

i given a virtual rooting of the tree. In particular, the

case sts(T

rooted

) = 2 (both children are tips) is par-

ticularly cheap to recompute, since tip vectors always

reside in RAM and recomputing ancestral vector i is

cheap (see above). In a perfectly balanced tree with

the root placed in the innermost branch, half of the

inner vectors have subtree size sts(T

rooted

) = 2.

As already mentioned, during a partial or full tree

traversal for computing the likelihood, all inner nodes

(vectors) involved are oriented in a given direction to-

ward the virtual root. Evidently, the subtree sizes will

change when the topology is altered and will need to

be updated accordingly.

In order to account for this, we keep an array of

subtree sizes, that is, for each inner node we store a

subtree size value. Whenever the topology changes, a

local traversal descriptor is created. This local traver-

sal descriptor starts at the new virtual root and recur-

sively includes the inner nodes whose orientation has

changed after the given topology change. Since this

exactly corresponds to the set of nodes whose subtree

size values must be updated, the subtree size array can

be updated via the same recursive descent.

3.5 Implementation Details

In the following we discuss some important details of

the recomputation process.

Largest Subtree First. The standard implementa-

tion of the PLF, where all ancestral vectors are avail-

able in memory, computes the PLF by conducting a

post-order traversal from an arbitrary rooting of the

tree. Thus, an ancestral probability vector can be

computed once the respective left and right child vec-

tors have been computed. In the standard RAxML

implementation, the traversal always recursively de-

scends into the left subtree ﬁrst. The (arbitrary)

choice whether to descend into the left or right sub-

tree ﬁrst, does not affect performance (nor the results)

when all ancestral vectors reside in RAM.

However, when not all vectors reside in RAM, the

choice whether to descend into the left or right subtree

ﬁrst does matter. This is particularly important if we

use the minimum setting x := log

(n)+ 2, since other-

wise we may encounter situations where not enough

slots are available (see Section 3.2).

Suppose that, as in the standard implementation,

TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC LIKELIHOOD COMPUTATIONS

virtual root

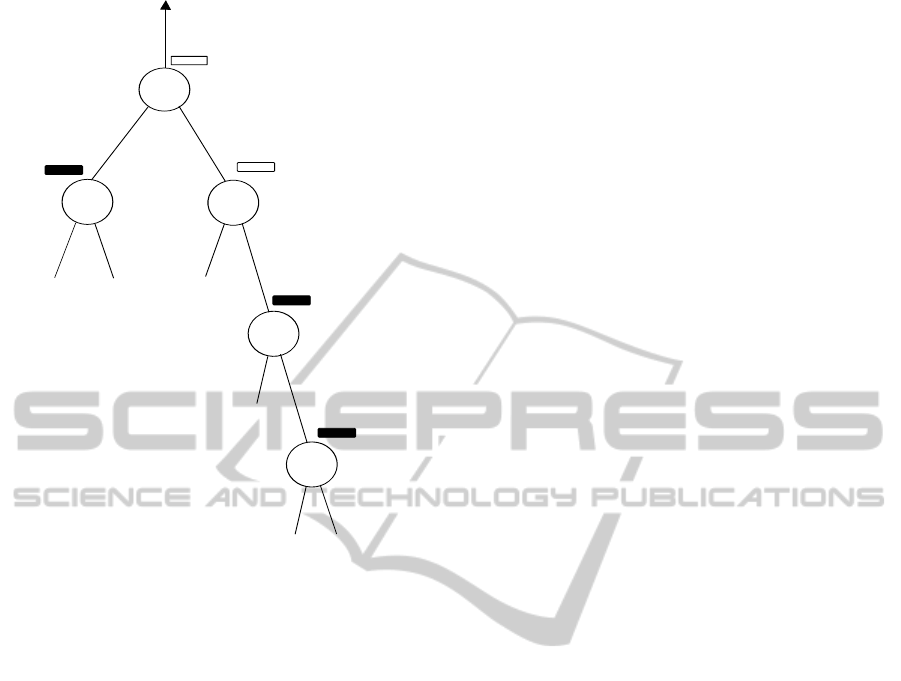
Figure 2: An unbalanced subtree, where the vector of inner

node 1 is oriented in the direction of the virtual root. Bold

rectangles represent vectors that must be held in memory if

we ﬁrst descend into the left subtree and node 4 is being

written.

we always descend into the left subtree ﬁrst. In the

example shown in Figure 2, the left subtree is signif-

icantly smaller than the right subtree. We would ﬁrst

descend into the left subtree, which consists of a sin-

gle inner node. The child ancestral vector correspond-

ing to node 2 must be pinned to its slot. Thereafter,

we descend into the right subtree writing and pinning

nodes 3, 4, 5 (always assuming that we descend into

the left —smaller— subtree of eachnode ﬁrst). While

we keep descending into the right subtree, the ances-

tral vector corresponding to node 2 remains pinned,

because it represents an intermediate result.

In contrast, if we initially descend into the right

subtree (which is always larger in the example), there

is no need to store intermediate results of the left sub-

tree (node 2). Also, nodes 4 and 5 can be imme-

diately unpinned as soon as their parent nodes have

been computed. Thus, by inverting the descent order

such as to always descend into the larger subtree ﬁrst

(as required by our proof), we minimize the amount

of time for which intermediate vectors must remain

pinned. Note that, when two subtrees have the same

size, it does not matter into which subtree we descend

ﬁrst.

If we descend into the smaller subtrees ﬁrst, there

will be more vectors that need to remain pinned for

a longer time. This would also reduce the effective

size of the set of inexpensive-to-recompute vectors

that shall preferentially be overwritten, because more

vectors that are cheap to recompute need to remain

pinned since they are holding intermediate results.

In this scenario more expensive-to-recompute vectors

will need to be overwritten in memory and dropped

from RAM.

Determining the appropriate descent order (largest

subtree ﬁrst) is trivial and induces a low compu-

tational overhead. When the traversal list is com-

puted, we simply need to compare the subtree sizes

of child nodes and make sure to always descend into

the largest subtree ﬁrst.

Priority List. For this additional optimization, we

exploit a property of the SPR move technique. When

a candidate subtree is pruned (removed from the cur-

rently best tree), it will be re-inserted into several

branches of the tree from which it was removed to

evaluate the likelihood of different placements of the

candidate subtree within this tree. In the course of

those insertions, the subtree itself will not be changed

and only the ancestral vector at the root of the subtree

will need to be accessed for computations. Hence, we

maintain a dedicated list of pruned candidate subtree

nodes (a unpinning priority list) that can be preferen-

tially unpinned. Because of the design of lazy SPR

moves in RAxML (similar SPR ﬂavors are used in

GARLI and PHYML) those nodes (corresponding to

ancestral vectors) will not be accessed while the can-

didate subtree is inserted into different branches of the

tree. Once this priority list is exhausted, the standard

MRC recomputation strategy is applied.

Full Traversals. Full post-order traversals of the

tree are required during certain phases of typical phy-

logenetic inference programs, for instance when op-

timizing global maximum likelihood model param-

eters (e.g., the α shape parameter of the Γ distribu-

tion or the rates in a GTR matrix) on the entire tree.

Full tree traversals are also important for the post-

analysis of ﬁxed tree topologies, for instance, to es-

timate species divergence times. Full tree traversals

represent a particular case because every inner vector

of the tree needs to be visited and computed. Hence,

the number of vectors that need to be computed under

our memory reduction approach is exactly identical to

the number of vectors that need to be computed under

the standard implementation. Thus, there is no need

for additional computations while a large amount of

memory can be saved. While full tree traversals do

not dominate run times in standard tree search algo-

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

rithms, they can dominate execution times in down-

stream analysis tools.

4 EXPERIMENTAL SETUP AND

RESULTS

We have implemented the techniques described in

Section 3 in RAxML-Light v1.0.4. RAxML-Light

is a strapped-down dedicated version of RAxML

intended for large-scale phylogenetic inferences

on supercomputers. It implements a light-weight

software-based checkpointing mechanism and offers

ﬁne-grained PThreads and MPI parallelizations

of the PLF. It has been used to compute a tree

on a dense simulated MSA with 1481 taxa and

20,000,000 sites that required 1TB of RAM and

ran in parallel with MPI on 672 cores. While not

yet published, RAxML-Light is available as open-

source code at www.exelixis-lab.org/software.html

and at https://github.com/stamatak. The source

code of the memory saving technique presented

here is available for download at www.exelixis-

lab.org/software/spare.zip and is currently being

integrated into the RAxML-Light development

version (development snapshots available at

https://github.com/ﬁzquierdo/vectorRecomp).

4.1 Evaluation of Recomputation

Strategies

The recomputation algorithm yields exactly the same

log likelihood scores for the PLF as the standard algo-

rithm. Thus, for validating the correctness of our im-

plementation, it is sufﬁcient to verify that the result-

ing trees and log likelihood scores of a ML tree search

with the standard and recomputation implementations

are identical. The increase of total run time depends

on the number x of inner vectors that are held in

memory and on the chosen unpinning strategy (MRC

versus RANDOM). We used indelible (Fletcher and

Yang, 2009) to generate simulated MSAs of 1500,

3000, and 5000 species. All experiments described in

this section were conducted for these three datasets.

We only show representative results for one dataset

(1500 taxa, 575 base pairs).

The results for the other two simulated datasets

(3000 taxa with 774 base pairs and 5000 taxa with

1074 base pairs), as well as for a biological dataset

with 500 taxa, are analogous and can be found in

the supplementary on-line material at www.exelixis-

lab.org/publications.html.

We chose to use simulated datasets to assess per-

formance for convenience. Detailed information on

indelible parameters used for dataset generation are

included in the supplementary on-line material. For

our purely computational work it does not matter

whether simulated or real data is used.

Initially, we ran the Parsimonator program (avail-

able at www.exelixis-lab.org/software.html to gener-

ate 10 distinct randomized stepwise addition order

parsimony starting trees for each MSA. For each

starting tree, we then executed a standard ML tree

search with RAxML-Light 1.0.4 (sequential version

with SSE3 intrinsics) and ML tree searches with the

recomputation version for the two replacement strate-

gies (MRC and RANDOM) and ﬁve different RAM

reduction factors (

-x

and

-r

options respectively).

In the recomputation version used for the evaluation,

both the Largest subtree ﬁrst and the Priority List op-

timizations were activated. All experiments were ex-

ecuted on a 48-core AMD system with 256GB RAM.

For all runs, RAM memory usage was measured ev-

ery 600 seconds with

top

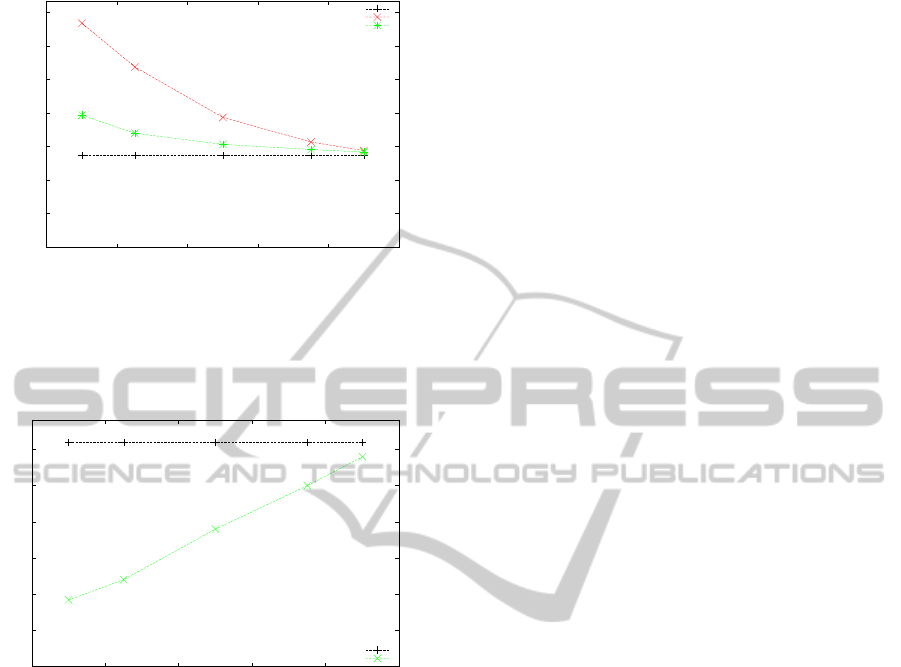
Figure 4 shows the corresponding decrease in

RAM usage. Values in Figure 4 correspond to maxi-

mum observed RAM usage values.

Figure 3 depicts the run time increase as a func-

tion of available space for storing ancestral proba-

bility vectors. Clearly, the MRC strategy outper-

forms the RANDOM strategy and the induced run-

time overhead, even for a reduction of available RAM

space to only 10% is surprisingly small (approxi-

mately 40%). This slowdown is acceptable, consid-

ering that instead of analyzing a large dataset on a

machine with 256GB, a signiﬁcantly smaller and less

expensive system with, for instance, 32GB RAM will

be sufﬁcient. Given the checkpointing capabilities of

RAxML-Light, the increase in run times does not rep-

resent a problem.

4.2 Evaluation of Traversal Overhead

In order to evaluate the overhead of the extended

(larger) tree traversals due to the required additional

ancestral probability vector computations, we modi-

ﬁed the source code to count the number of ancestral

vector computations. We distinguish between three

cases with different recomputation costs (see Sec-

tion 3). For each case, there exists a dedicated PLF

implementation in RAxML.

Tip/Tip Both child nodes are tips.

Tip/Vector One child node is a tip, and the other is

an ancestral vector (subtree).

Vector/Vector Both child nodes are ancestral vec-

tors.

TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC LIKELIHOOD COMPUTATIONS

2000

4000

6000

8000

10000

12000

14000

0 0.2 0.4 0.6 0.8 1

Average Running time (s)

Reduction Factor (% inner vectors on RAM)

Strategy performance for 10 runs of dataset 1500

std

recomRANDOM

recomSLOT_MIN_COST

Figure 3: Different replacement strategies. The dataset was

run with RAM allocations of 10%, 25%, 50% , 75%, and

90%, of the total required memory for storing all probability

vectors. Run times are averaged across 10 searches with

distinct starting trees.

0 0.2 0.4 0.6 0.8 1

Average Memory used (MB)

Reduction Factor (% inner vectors on RAM)

Memory measured for dataset 1500 for 10 trees

std

recomSLOT_MIN_COST

Figure 4: Overall RAM usage when allocating only 10%,

25%, 50% , 75%, and 90%, of the required ancestral proba-

bility vectors.

Table 1 shows a dramatic, yet desired increase,

in the number of Tip/Tip vector computations for the

MRC strategy. However, the amount of the slowest

type of ancestral node computations [Vector/Vector]

is only increased by 0.16% compared to the standard

implementation.

4.3 Evaluation of Full Tree Traversals

We created a simple test case that parses an input tree

and conducts 20 full tree traversals on the given tree.

This dedicated test code is also available at

https:

//github.com/fizquierdo/vectorRecomp/

. We

used the aforementioned starting trees and the 500,

1500, and 5000 taxon datasets. Each run was repeated

5 times and we averaged running times. All runs re-

turned exactly the same likelihood scores.

Table 2 indicates that, even for very small R values

(fraction of inner vectors allocated in memory) the run

time overhead is negligible compared to the standard

implementation.

5 CONCLUSIONS AND FUTURE

WORK

We have presented a generic strategy for the exact

computation of log likelihood scores and ML tree

searches with signiﬁcantly reduced memory require-

ments. The additional computational cost incurred

by the larger number of required ancestral vector re-

computations is comparatively low when an appro-

priate vector replacement strategy is deployed. This

will allow for computing the PLF on larger datasets

than ever before, especially when the limiting factor is

available RAM. In fact, the memory versus additional

computationstrade-off can be adapted by the users via

a command line switch to ﬁt their computational re-

sources. We also show that, the minimum number of

ancestral probability vectors for computing the PLF

that need to be kept in memory for a tree with n taxa

is log

(n) + 2. This result may be particularly inter-

esting for designing equally fast, but highly memory-

efﬁcient phylogenetic post-analysis tools that rely on

full tree traversals.

Furthermore, the concepts presented here can be

applied to all PLF-based programs such as GARLI,

PHYML, MrBayes, etc. On the software engineering

side, the implementation of the recomputation strat-

egy in RAxML is encapsulated in such a way, that

it can be combined with any other memory saving

techniques such as out-of-core computations, Subtree

Equality Vectors, or the use of lossless compression

algorithms for ancestral probability vectors.

We plan to further reﬁne/tune the MRC strategy

and fully integrate it into the up-to-date release of

RAxML-Light v1.0.5 and the already existing mem-

ory saving techniques. This will allow to infer trees

and compute likelihood scores on huge datasets, that

would previously have required a supercomputer, on

a single multi-core system.

ACKNOWLEDGEMENTS

Fernando Izquierdo-Carrasco is funded by the Ger-

man Science Foundation (DFG). The authors would

like to thank Simon Berger for pointing out and dis-

cussing favorable trade-offs regarding recomputation

of vectors and the potential use of lossless compres-

sion algorithms to decrease memory requirements.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

Table 1: Frequency of ancestral vector cases for the standard implementation and the recomputation strategies (50% of

ancestral vectors allocated).

Strategy Tip/Tip Tip/Vector Vector/Vector Total Runtime (s)

Standard 11,443,484 57,884,490 76,325,233 145,653,207 5678

MRC (0.5) 20,368,957 61,224,562 76,444,874 158,038,393 6453

Random (0.5) 37,778,575 85,303,730 104,398,910 227,481,215 7999

Table 2: Average run times in seconds for 20 full traversals averaged across 5 runs.

Dataset Standard R:=0.1 R:=0.9

500 0.122 0.121 0.130

1500 0.430 0.430 0.434

5000 2.402 2.412 2.438

REFERENCES

Barkan, E., Biham, E., and Shamir, A. (2006). Rigorous

bounds on cryptanalytic time/memory tradeoffs. In In

Advances in CryptologyCRYPTO 2006, volume 4117

of LNCS, pages 1–21. Springer-Verlag.

Berger, S. and Stamatakis, A. (2010). Accuracy and

performance of single versus double precision arith-

metics for Maximum Likelihood Phylogeny Recon-

struction. Springer Lecture Notes in Computer Sci-

ence, 6068:270–279.

Dri, P. and Galil, Z. (1984). A time-space tradeoff for

language recognition. Theory of Computing Systems,

17:3–12. 10.1007/BF01744430.

Felsenstein, J. (1981). Evolutionary trees from DNA se-

quences: a maximum likelihood approach. J. Mol.

Evol., 17:368–376.

Fletcher, W. and Yang, Z. (2009). INDELible: a ﬂexible

simulator of biological sequence evolution. Molecular

biology and evolution, 26(8):1879–1888.

Guindon, S., Dufayard, J., Lefort, V., Anisimova, M.,

Hordijk, W., and Gascuel, O. (2010). New algorithms

and methods to estimate maximum-likelihood phylo-

genies: assessing the performance of PhyML 3.0. Sys-

tematic biology, 59(3):307.

Izquierdo-Carrasco, F. and Stamatakis, A. (2011). Comput-

ing the phylogenetic likelihood function out-of-core.

In In Proceedings of the IPDPS-HiCOMB 2011.

Martin Simonsen, T. M. and Pedersen, C. N. S. (2010).

Building very large neighbour-joining trees. Proceed-

ings of Bioinformatics 2010, to appear in Springer

bioinformatics lecture notes.

Stamatakis, A. (2006). RAxML-VI-HPC: maximum

likelihood-based phylogenetic analyses with thou-

sands of taxa and mixed models. Bioinformatics,

22(21):2688–2690.

Stamatakis, A. (2011). Phylogenetic Search Algorithms for

Maximum Likelihood, pages 547–577. John Wiley &

Sons, Inc.

Stamatakis, A. and Alachiotis, N. (2010). Time and mem-

ory efﬁcient likelihood-based tree searches on phy-

logenomic alignments with missing data. Bioinfor-

matics, 26(12):i132.

Stamatakis, A. and Ott, M. (2008). Exploiting ﬁne-grained

parallelism in the phylogenetic likelihood function

with mpi, pthreads, and openmp: a performance study.

Pattern Recognition in Bioinformatics, pages 424–

435.

Vitter, J. S. (2008). Algorithms and data structures for ex-

ternal memory. Found. Trends Theor. Comput. Sci.,

2(4):305–474.

Wheeler, T. (2009). Large-scale neighbor-joining with

ninja. In Salzberg, S. and Warnow, T., editors, Al-

gorithms in Bioinformatics, volume 5724 of Lecture

Notes in Computer Science, pages 375–389. Springer

Berlin / Heidelberg.

Xu, J. and Lipton, R. J. (2005). On fundamental tradeoffs

between delay bounds and computational complexity

in packet scheduling algorithms. IEEE/ACM Trans.

Netw., 13:15–28.

Yang, Z. (1994). Maximum likelihood phylogenetic esti-

mation from DNA sequences with variable rates over

sites. J. Mol. Evol., 39:306–314.

Zwickl, D. (2006). Genetic Algorithm Approaches for the

Phylogenetic Analysis of Large Biological Sequence

Datasets under the Maximum Likelihood Criterion.

PhD thesis, University of Texas at Austin.

TRADING RUNNING TIME FOR MEMORY IN PHYLOGENETIC LIKELIHOOD COMPUTATIONS