TERMINATION OF SIMULATED ANNEALING ALGORITHM

SOLVING SEMI-SUPERVISED LINEAR SVMS PROBLEMS

Vaida Bartkute-Norkuniene

Vilnius University, Institute of Informatics and Mathematics, Vilnius, Lithuania

Utena University of Applied Sciences, Utena, Lithuania

Keywords: Order Statistics, Continuous Optimization, Simulated Annealing, Semi-supervised SVMs Classification.

Abstract: In creating heuristic search algorithms one has to deal with the practical problem of terminating and

optimality testing. To solve these problems, we can use information gained from the set of the best function

values (order statistics) provided during optimization. In this paper, we consider the application of order

statistics to establish the optimality in heuristic optimization algorithms and to stop the Simulated Annealing

algorithm when the confidence interval of the minimum becomes less than admissible value. The accuracy

of the solution achieved during optimization and the termination criterion of the algorithm are introduced in

a statistical way. We build a method for the estimation of confidence intervals of the minimum using order

statistics, which is implemented for optimality testing and terminating in Simulated Annealing algorithm. A

termination criterion - length of the confidence interval of the extreme value of the objective function - is

introduced. The efficiency of this approach is discussed using the results of computer modelling. One test

function and two semi-supervised SVMs linear classification problems illustrate the applicability of the

method proposed.

1 INTRODUCTION

The termination problem is topical in stochastic and

heuristic optimization algorithms. Note, values of

the objective function provided during optimization

contain important information on the optimum of the

function and, thus, might be applied to algorithm

termination. Mockus (Mockus, 1967), Zilinskas and

Zhigljavsky (Zilinskas & Zhigljavsky, 1991) were

the first who proposed statistical inferences for

optimality testing in optimization algorithms using

theory of order statistics. These inferences were

studied by computer simulation (see, Bartkute et al,

2005, Bartkute & Sakalauskas, 2009), which

confirmed theoretical assumption about the

distribution of order statistics with respect to

extreme value distribution. Thus, the estimate of

extremum value of the objective function and its

confidence interval were proposed following to

latter assumption. Besides, in Bartkute &

Sakalauskas (Bartkute & Sakalauskas, 2009a) it was

proposed to terminate the stochastic optimization

algorithm, when the confidence interval of the

extremum

becomes less than prescribed value. Since

theoretical analysis of the optimal decision

making

algorithm is complicated, computer modelling

becomes an important research method that enable

us to test and study hypotheses arising from the

problem discussed above. Semi-supervised SVMs

linear classification problems as an examples

illustrate the applicability of the method proposed.

2 METHOD FOR TESTING THE

OPTIMALITY

Assume, the optimization problem is (minimization)

(

)

min→xf

(1)

where

ℜ→ℜ

f : is a function bounded from

below,

()

−∞>=

⎟

⎠

⎞

⎜

⎝

⎛

ℜ∈

Axfxf

min

, ∞<

x . Let

this problem be solved by the Markov type

algorithm providing a sample

{}

, ... ,

=Η ,

whose elements are function values

)(

Our approach is grounded by the assumption on the

asymptotic distribution of order statistics according

to the Weibull (Weibull, 1951) distribution

150

Bartkute-Norkuniene V..

TERMINATION OF SIMULATED ANNEALING ALGORITHM SOLVING SEMI-SUPERVISED LINEAR SVMS PROBLEMS.

DOI: 10.5220/0003759301500156

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 150-156

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

()

,0,,0,1,,, >≥>−=

−⋅−

cAxeAcxW

Axc

αα

where

c, A and α denote the scale, location and

shape parameters, respectively (see for details

Bartkute & Sakalauskas, 2009a). The Weibull

distribution is one of the extreme-value distributions

which is applied also in optimality testing of Markov

type optimization algorithms. Although this limit

distribution of extreme values is studied mostly for

i.i.d. values, it also might be often used in the

absence of the assumption of independence

(Galambosh, 1984).

To estimate confidence intervals for the

minimum

A of the objective function, it suffices to

choose from sample H only

k+1 the best function

values

NkN ,

, ... ,

, from the ordered

sample

NNNkNN ,

...

,...,

,1,0

≤≤≤≤≤ ,

where

()

Nkk = , +∞→→ N,

(Zilinskas &

Zhigljavsky, 1991, Bartkute & Sakalauskas, 2009a).

Then the linear estimators for A can be as follows:

()

⎟

⎠

⎞

⎜

⎝

⎛

−⋅−=

,,0

ηηη

(2)

where coefficient

can be estimated as

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅

∏

is the shape parameter of

distribution of the extreme values,

is the

parameter of homogeneity of the function

(

)

xf in

the neighbourhood of the point of

minimum:

()

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

−

xxOxfxf

(Zilinskas &

Zhigljavsky, 1991, Bartkute & Sakalauskas, 2009a).

The one-side confidence interval of the

minimum of the objective function is as follows:

[

NNNk

N ,0

,0,

ηηη

⎟

⎠

⎞

⎜

⎝

⎛

−⋅−

]

(3)

where

() ()

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−−=

αα

δδ

11111

the confidence level.

The estimates introduced here might be used to

create the termination criterion for the stochastic and

heuristic optimization algorithms, namely, the

algorithm stops, when the length of the confidence

interval becomes less than prescribed value

3 DESCRIPTION OF SIMULATED

ANNEALING ALGORITHM

Let us consider an application of this approach to

continuous global optimization by the Simulated

Annealing algorithm (SA). This is a well-known

Markov type algorithm for random optimization.

Simulated Annealing (SA) is widely applied in

multiextremal problems. Conditions of global

convergence of SA are studied by many authors

(Granville et al., 1994, Yang, 2000, etc.). We use the

modification of SA, developed by Yang (2000),

where the function regulating the neighbourhood

depth of solution is introduced together with the

temperature regulation function. The procedure of

the SA algorithm consists of the following steps:

Step 1. Choose an initial point

Dx ℜ⊂∈

, an

initial temperature value

, a kind of

temperature-dependent generation probability

density function, a corresponding temperature

updating function, and a sequence

}0,{ ≥t

monotonically decreasing positive numbers,

describing the neighboring states. Calculate

)(

Set

t .

Step 2. Generate a random vector

z by using

the generation probability density function. If there

exists i such that

ni ≤≤1

, where

is the

component of the vector

, repeat Step 2.

Otherwise, generate a new trial point

by adding

the random vector

to the current iteration point

ttt

zxy +=

(4)

∉ , repeat Step 2; otherwise, calculate

)(

yf .

Step 3. Use the Metropolis acceptance criterion

to determine a new iteration point

1+t

[10].

Specifically, generate a random number

with the

uniform distribution over [0,1], and then calculate

the probability

(

)

TxyP ,,

of accepting the trial

point

y as the new itteration point

1+t

, given

x and

T ,

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

yfxf

TxyP

)()(

exp,1min),,(

TERMINATION OF SIMULATED ANNEALING ALGORITHM SOLVING SEMI-SUPERVISED LINEAR SVMS

PROBLEMS

151

(

)

TxyP ,,≤

, set

yx =

and

(

)

(

)

yfxf =

; otherwise, set

xx =

and

(

)

(

)

xfxf =

Step 4.

If the prescribed termination condition is

satisfied, then stop; otherwise, update the value of

the temperature by means of the temperature

updating function, and then go back to Step 2.

Thus, by applying the generation mechanism and

the Metropolis acceptance criterion, the SA

algorithm produces two sequences of random points.

These are the sequence

{

}

0, ≥ty

of trial points

generated by (4) and the sequence

{

}

0, ≥tx

iteration points determined by applying the

Metropolis acceptance criterion as described in Step

3. These two sequences of random variables are all

dependent on the temperature sequence

{

}

0, ≥tT

determined by the temperature updating function,

the state neighbouring sequence

{}

0, ≥t

, and the

approach of random vector generation.

The sequence

{}

0, ≥t

of positive numbers

specified in Step 1 of the above SA algorithm is

used to impose a lower bound on the random vector,

generated at the each iteration, for obtaining the

random trial point. This lower bound should be

small enough and monotonically decreasing as the

annealing proceeds. Since the temperature-

dependent generation probability density function is

used to generate random trial points and since only

one trial point is generated at each temperature value

the SA algorithm considered is characterized by a

nonhomogeneous continuous-state Markov chain.

The convergence conditions of the SA were

studied by Yang (Yang, 2000) and several updating

functions for the method parameters were given,

which ensure convergence of the method. We

applied the next updating functions in testing our

approach.

Let

r ℜ∈

, with component

Dyx

yxr −=

∈,

max

ni ≤≤1

1>d

1>u

≤≤

min0

⋅

−

⋅=

ρρ

for all

1≥t

, where

{}

0, ≥t

is the sequence used to impose lower

bounds on the random vectors generated in the SA

algorithm. Let the temperature-dependent generation

probability density function

()

Tp ,⋅

be given by

.,1log1

)1(

),(

Tzp ℜ∈

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+⋅

−

∏

Then, for any initial point

Dx ∈

, the sequence

{

}

0);( ≥txf

of objective function values converges

in probability to the global minimum

, if the

temperature sequence

{

}

0, ≥tT

determined by the

temperature updating function satisfies the following

condition:

⎟

⎠

⎞

⎜

⎝

⎛

⋅−⋅=

⋅nd

tlTT

exp

...,,,i 21=

where

is the initial temperature value and

0>l

is a given real number (Yang, 2000).

Typically a different form of the temperature

updating function has to be used with respect to a

different kind of the generation probability density

function in order to ensure the global convergence of

the corresponding SA algorithm. Furthermore, the

flatter is the tail of the generation probability

function, the faster is the decrement of the

temperature sequence determined by the temperature

updating function.

4 SVM CLASSIFICATION

Data classification is a common problem in science

and engineering. Support Vector Machines (SVMs)

are powerful tools for classifying data that are often

used in data mining operations.

In the standard binary classification problem, a

set of training data

(

)

y,u , … ,

(

)

y,u is

observed, where the input set of points is

Uu ℜ⊂∈ , the

y is either +1 or −1, indicating

the class to which the point

u belongs,

{

}

11 −+∈ ,y

. The learning task is to create the

classification rule

{}

11 −+→ ,U:f that will be

used to predict the labels for new inputs. The basic

idea of SVMs classification is to find a maximal

margin separating hyperplane between two classes.

It was first described by Cortes and Vapnik (Cortes

& Vapnik, 1995). The standard binary SVM

classification problem is shown visually in Figure 1.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

152

Figure 1: Linear separating hyperplanes for a separable

case.

4.1 Semi-supervised Linear SVMs

There are a lot of classification problems where data

labeling is hard or expensive, while unlabeled data is

often abundant and cheap to collect. The typical

areas where this happens is the speech processing,

text categorization, webpage classification, business

risk identification, credit scoring and, finally, a

bioinformatics area where it is usually both

expensive and slow to label huge number of data

produced. When data points consist of exactly two

sets: one set that has been labeled by a decision

maker and the other that is not classified, but

belongs to one known category we have a traditional

semi-supervised classification problem (Bennett &

Demiriz (1999), Huang & Kecman (2004)). The goal

of semi-supervised classification is to use unlabeled

data to improve the performance of standard

supervised learning algorithms. In semi-supervised

learning the data set

{

}

can be divided into

two parts: the training set consists of

p labelled

examples

(){}

y,u

1±=

, and of m unlabeled

examples

{}

1+=

, with m

n += . The learning

task is to create the classification rule

{}

11 −+→ ,U:f

that will be used to predict the

labels for new inputs. To solve that problem we may

rewrite standard binary classification problem

(Cortes & Vapnik, 1995) in the following

unconstrained form (Astorino & Fuduli, 2007,

Bartkute-Norkuniene, 2009b):

()

bwf

,min

, ℜ∈ℜ∈

where

()

()()

++⋅⋅⋅+=

∑

iTi

buwyLC

bwf

∑

⎟

⎠

⎞

⎜

⎝

⎛

+⋅⋅+

buwLC

and b are both the hyperplane parameters,

(

)

(

)

t,maxtL

−

(

) ()

t,maxtL −= 10

are the loss

functions,

≥≥ CC

are certain penalty

coefficients,

p is the size of training set, and m is the

size of testing set. The first two terms in the

objective function

(

)

b,wf

define the standard SVM,

and the third one incorporates unlabelled (testing)

data. The error over labelled and unlabelled

examples is weighted by two parameters

and C

This form seems advantageous especially when the

input dataset is very large.

5 COMPUTER MODELLING

The empirical evidence of our approach, using two

test functions, synthetic and real datasets, is

provided and discussed in this Section. To evaluate

the performance of our proposed algorithm in

practice, we analyze two machine learning datasets.

Example 1: test function (Zhigljavsky &

Zilinskas, 2007)

()

()()

()

⎪

⎩

⎪

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

−

∈−

⎥

⎦

⎤

⎢

⎣

⎡

−−−

∈

⎟

⎠

⎞

⎜

⎝

⎛

−

⎥

⎦

⎤

⎢

⎣

⎡

−−

∈

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

sin

sin1

sin

xforxl

xfor

xls

xfor

xls

For all integer

2, ≥ls

, the functions

()

(

)

ls,

are continuously differentiable in the set

[]

1,0

and

have three local minima. These local minima are

achieved at the points:

(

)

(

)

(

)( )

112

321

−=

−−

−

Global minimum is at the point

and equal to

0. Despite the fact that the functions

()

(

)

ls,

are

continuously differentiable, the problem of finding

the minimum point is very difficult when

k is large.

Example 2: The Rastrigin function

() ( )

(

)

∑

⋅−+=

xxnxf

2cos1010

, search domain

2,12.512.5 =≤≤− nx

, the minimum is 0.

TERMINATION OF SIMULATED ANNEALING ALGORITHM SOLVING SEMI-SUPERVISED LINEAR SVMS

PROBLEMS

153

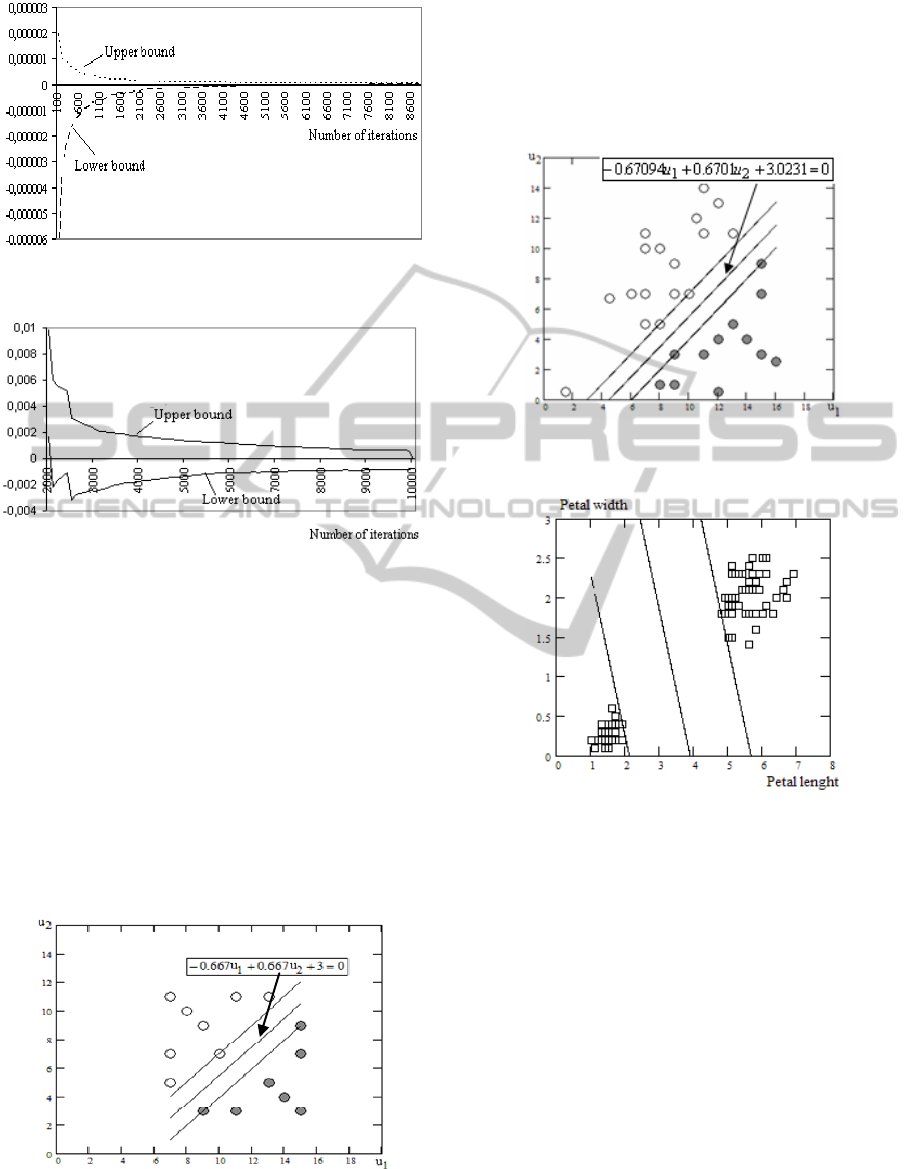
Figure 2: Confidence bounds of the minimum (Example 1,

s=12, l=5).

Figure 3: Confidence bounds of the minimum (Example

2).

Test functions were minimized, with the number

of iterations

N =10000 and the number of trials

M=500, starting from points randomly distributed in

the search domain. Results of the estimate (2) of the

test functions minimum value

and the estimate

(3) of the confidence interval are presented in Table

1 and Figures 2 and 3. These results show that the

proposed estimates approximate the confidence

interval of the objective function minimum value

rather well, and that the length of the confidence

interval decreases when the number of iterations

increases.



Figure 4: Linear separating hyperplanes of training data.

Example 3: linear example (V. Bartkute-

Norkuniene (2009). The linear separating

hyperplanes of training data are demonstrated in

Figure 4. Figure 5 illustrates that the SA classifier

for training and testing datasets is close to an

optimal decision boundary.

Figure 5: Linear separating hyperplanes of the training and

testing data.

Figure 6: Linear separating hyperplanes for two

dimensional Iris Plant data,

b= 2.1830, w

=-0.5625,

= -0.2741.

Example 4: dataset of Iris Plants (Asuncion &

Newman, 2007). The dataset contains 3 classes of 50

instances each, where each class refers to a type of

iris plant. One class is linearly separable from the

other two, the latter are not linearly separable from

each other. In our approach for the binary

classification we use only two classes of iris plant:

iris Setosa (the class +1) and iris Virginica (the class

-1).

Linear separating hyperplanes for two-

dimensional Iris Plant data are illustrated in Figure

6. These results illustrate the applicability of SA

algorithm for Semi-supervised SVM classification.

In Figure 7,

we can see histograms of the number

of iterations after termination of the SA algorithm

depending on the length of the confidence interval.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

154

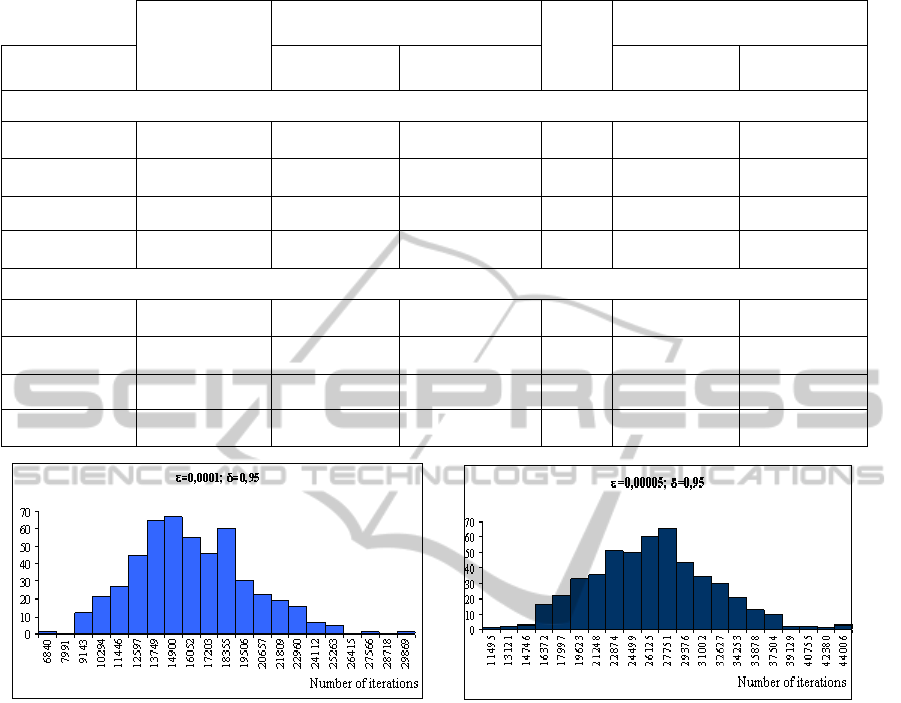
Table 1: Computer modelling results of the minimum value and the confidence interval.

Confidence interval

Confidence interval of the hitting

probability p

Confidence

probability

Lower bound Upper bound Lower bound Upper bound

Example 1

9.0=

-0.0000000307 -0.000000483 0.0000002275 0.91 0.8614377 0.94498488

95.0=

0.0000000005 -0.00000002 0.0000000072 0.95 0.89763031 0.98009752

975.0=

-0.000000031 -0.00000151 0.0000002275 0.98 0.92955759 0.9975685

99.0=

-0.000000031 -0.00000239 0.0000002275 0.98 0.91852038 0.99850762

Example 2

9.0=

0.0000478328 -0.00077633 0.000620020 0.886 0.90384692 0.86549069

95.0=

0.0000478328 -0.00122913 0.000620020 0.948 0.92806921 0.96283961

975.0=

0.0000478328 -0.00169791 0.000620020 0.97 0.95099096 0.98311659

99.0=

0.0000478328 -0.00234306 0.000620020 0.984 0.96551508 0.99416328

Figure 7: The number of iterations after termination of the algorithm (two dimensional Iris Plant data).

6 CONCLUSIONS

A linear estimator and confidence bounds for the

minimum value of the function have been proposed,

using order statistics of the function values provided

by SA algorithm, which were studied in an

experimental way. These estimators are simple and

depend only on the parameter of the extreme value

distribution

α. The latter parameter α is easily

estimated, using the parameter of homogeneity of

the objective function or in a statistical way.

Theoretical considerations and computer examples

have shown that the confidence interval of the

function minimum can be estimated with an

admissible accuracy, when the number of iterations

is increased. Empirical study of the statistical

hypothesis on order statistics have shown that

function values lead us to a conclusion that the

estimates proposed can be applied in optimality

testing and termination of the SA algorithm. The

estimates introduced here can be used to create the

termination criterion for SA algorithm, namely, the

algorithm stops, when the length of the confidence

interval becomes smaller than prescribed value

REFERENCES

Astorino, A., Fuduli, A., 2007. Nonsmooth Optimization

Techniques for Semisupervised Classification.

IEEE

Transactions on Pattern Analysis and Machine

Intelligence, vol. 29, No. 12, p. 2135-2142.

Asuncion, A., Newman, D. J., 2007.

UCI Machine

Learning Repository

. School of Information and

Computer Science

, University of California, Irvine,

CA. (http://www.ics.uci.edu/˜mlearn/ MLRepository.

html)

TERMINATION OF SIMULATED ANNEALING ALGORITHM SOLVING SEMI-SUPERVISED LINEAR SVMS

PROBLEMS

155

Bartkutė, V., Sakalauskas, L., 2004. Order statistics for

testing optimality in stochastic optimization.

Proceedings of the 7

International Conference

Computer data analysis and Modelling”

, Minsk, p.

128-131

Bartkute, V., Sakalauskas, L., 2009a. Statistical Inferences

for Termination of Markov Type Random Search

Algorithms. Journal of Optimization Theory and

Applications

, vol. 141, p. 475-493.

Bartkutė-Norkuniene V., 2009b. Stochastic Optimization

Algorithms for Support Vector Machines

Classification.

Informatica, vol. 20, No. 2, p. 173–186.

Bennett, K. P., Demiriz, A., 1999. Semi-supervised

support vector machines. In M. S. Kearns, S. A. Solla,

and D. A. Cohn, editors,

NIPS, vol. 11, p. 368–374.

Cortes, C., Vapnik, V., 1995. Support-vector networks.

Machine Learning, vol. 20, No. 3, p. 273-297.

Galambosh, Y., 1984.

Asymptotic Theory of Extremal

Order Statistics

, Nauka, Moscow (in Russian).

Granville, V., Krivanek, M., Rasson, J. P., 1994.

Simulated annealing: a proof of convergence. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, vol 16, No. 6, p. 652–656.

Hall, P., 1982. On estimating the endpoint of a

distribution. Annals of Statistic, vol. 10, p. 556-568.

Huang, T. M., Kecman, V., 2004. Semi-supervised

Learning from Unbalanced Labeled Data – An

Improvement, in 'Knowledge Based and Emergent

Technologies Relied Intelligent Information and

Engineering Systems', Eds. Negoita, M. Gh., at al.,

Lecture Notes on Computer Science, vol. 3215, p.

765-771.

Mockus, J., 1967. Multi-Extremal Problems in

Engineering Design

. Nauka, Moscow, (in Russian).

Yang, R. L., 2000. Convergence of the simulated

annealing algorithm for continuous global

optimization.

Journal of Optimization Theory and

Applications

, vol. 104, No. 3, p. 691–716.

Zilinskas, A., Zhigljavsky, A., 1991.

Methods of the

global extreme searching

. Nauka, Moscow, (in

Russian).

Zilinskas, A., Zhigljavsky, A., 2007.

Stochastic global

optimization

. Springer.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

156