MAXIMUM LIKELIHOOD ESTIMATION OF MULTIVARIATE
SKEW T-DISTRIBUTION
Leonidas Sakalauskas and Ingrida Vaiciulyte
Institute of Mathematics and Informatics, Vilnius University, Akademijos 4, Vilnius, Lithuania
Keywords: Monte – Carlo Markov chain, Skew t distribution, Maximum likelihood, Gaussian approximation, EM –
algorithm, Testing hypothesis.
Abstract: The present paper describes the Monte – Carlo Markov Chain (MCMC) method for estimation of skew t –
distribution. The density of skew t – distribution is obtained through a multivariate integral, using
representation of skew t – distribution by a mixture of multivariate skew – normal distribution with the
covariance matrix, depending on the parameter, distributed according to the inverse – gamma distribution.
Next, the MCMC procedure is constructed for recurrent estimation of skew t – distribution, following the
maximum likelihood method, where the Monte – Carlo sample size is regulated to ensure the convergence
and to decrease the total amount of Monte – Carlo trials, required for estimation. The confidence intervals of
Monte – Carlo estimators are introduced because of their asymptotic normality. The termination rule is also
implemented by testing statistical hypotheses on an insignificant change of estimates in two steps of the
procedure.
1 INTRODUCTION
Stochastic optimization plays an increasing role in
modeling and statistical analysis of complex
systems. Conceptually, detection of structures in real
– life data is often formulated in the framework of
combinatorial or continuous optimization by using
the following stochastic techniques: Monte – Carlo
Markov chains, Metropolis – Hastings algorithm,
stochastic approximation, etc. (Rubinstein and
Kroese, 2007; Spall, 2003). In the present paper the
maximum likelihood approach for estimating the
parameters of the multivariate skew t – distribution
is developed, using the adaptive Monte – Carlo
Markov chain approach. Multivariate skew t –
distribution is often applied in the analysis of
parametric classes of distributions that exhibit
various shapes of skewness and kurtosis (Azzalini
and Genton, 2008; Cabral, Bolfarine and Pereira,
2008). In general, the skew t – distribution is
represented by a multivariate skew – normal
distribution with the covariance matrix, depending
on the parameter, distributed according to the
inverse – gamma distribution. According to this
representation, the density of skew t – distribution as
well as the likelihood function are expressed through
multivariate integrals that are convenient to be
estimated numerically by Monte – Carlo simulation.
Denote the skew t – variable by
),,,( bST ΘΣ
μ
. In
general, a multivariate skew t – distribution defines a
random vector
X
that is distributed as a multivariate
Gaussian vector:
)()(
2
1
2
1
)/(),,,(
axaxt
d
T
ettaxf
−⋅Σ⋅−⋅−
−
−
⋅Σ⋅=Σ π
(1)
where the vector of mean
a
, in its turn, is
distributed as a multivariate Gaussian
() tN 2/,Θ μ
in
the half – plane
0)( ≥
−
⋅
μ
aq
, where
,
d
Rq ⊂
0,0 ≥
Θ
≥
Σ
are the full rank
dd ×
matrices,
d
is the
dimension, and the random variable
t
follows from
the Gamma distribution:
t
b
e
b
t
btf
−
−
⋅
Γ
=
)2/(
),(
1
2
1
(2)
By definition,
d
– dimensional skew t –
distributed variable
X
has the density:
∫∫
∞
≥−⋅
⋅Θ⋅Σ⋅=ΘΣ
00)(
1
),(),,,(),,,(2),,,,(
μ
μμ
aq
dadtbtftaftaxfbxp
(3)
This distribution is often considered in the
statistical literature, where it is applied in financial
forecasting (Azzalini and Capitanio, 2003; Azzalini
and Genton, 2008; Kim and Mallick, 2003;
Panagiotelis and Smith, 2008).
200
Sakalauskas L. and Vaiciulyte I..
MAXIMUM LIKELIHOOD ESTIMATION OF MULTIVARIATE SKEW T-DISTRIBUTION.
DOI: 10.5220/0003727002000203
In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 200-203
ISBN: 978-989-8425-97-3
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 THE MAXIMUM LIKELIHOOD
ESTIMATION OF
MULTIVARIATE SKEW
T – DISTRIBUTION
Let a matrix of observations be
given
⎟
⎠
⎞
⎜
⎝
⎛
=
K
XXXX ,...,
2
,
1
, where
i
X
independent
vectors, distributed as
),,,( bST ΘΣ
μ
. We will examine
the estimation of parameters
b,,, ΘΣ
μ
, following to
maximum likelihood approach. The log – likelihood
function can be expressed as:
b
K
i
i
bXpbL
,,,
1
max)),,,,(ln(),,,(
ΘΣ
=
→ΘΣ−=ΘΣ
∑
μ
μμ
(4)
The optimality conditions in this problem are
derived by taking and setting the first derivatives
with respect to parameters to be estimated equal to
zero. Then the maximum likelihood estimates
(MLE)
b
ˆ
,
ˆ
,
ˆ
,
ˆ
ΘΣ μ
of parameters of multivariate skew t
– distribution (3) are found by solving the equations,
obtained in this way, subject to
0,0 ≥
Θ
≥Σ
.
Derivatives of the likelihood function are expressed
through derivatives of the density function. By
virtue of the Euler’s formula the skew t –
distribution density is as follows:
∫
∏
≥−⋅
+
−
=
⋅Θ⋅Σ⋅
⎟
⎠
⎞
⎜
⎝
⎛
+⋅
=ΘΣ
0)(
2
2
1
2
1
1
0
2
2
),,,,(
μ
π
μ
aq
d
b
d
d
i
da
A
i
b
bxp
(5)
where
.1)()()()(
11
+−⋅Θ⋅−+−⋅Σ⋅−=
−−
μμ aaaxaxA
TT
After differentiation of this expression and using
the Euler’s formula again, we have:
dadtbtftaftaxfaxt
bxp
aq
),(),,,(),,,()(
),,,,(
1
00)(
1
⋅Θ⋅Σ⋅−⋅Σ⋅=
∂
ΘΣ∂
∫∫
∞
≥−⋅
−
μ
μ
μ
μ
(6)
()
dadtbtftaftaxf
axaxt
bxp
aq
T
),(),,,(),,,(
)()(
),,,,(
1
00)(
111
⋅Θ⋅Σ×
×Σ⋅−⋅−⋅Σ⋅+Σ−=
Σ∂
ΘΣ∂
∫∫
∞
≥−⋅
−−−
μ
μ
μ
(7)
()
dadtbtftaftaxf
aat
bxp
aq
T
),(),,,(),,,(
)()(
),,,,(
1
00)(
111
⋅Θ⋅Σ×
×Θ⋅−⋅−⋅Θ⋅+Θ−=
Θ∂
ΘΣ∂
∫∫
∞
≥−⋅
−−−
μ
μμ
μ
μ
(8)
dadtbtftaftaxf
i
b
A
b
bxp
aq
d
i
),(),,,(),,,(
2
1
)ln(
),,,,(
1
00)(
1
0
⋅Θ⋅Σ×
×
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
+−=
∂
ΘΣ∂
∫∫
∑
∞
≥−⋅
−
=
μ
μ
μ
(9)
Let us introduce the conditional density:
),,,,(
),(),,,(),,,(2
),,,,,(
1
bxp
btftaftaxf
xbtaf
ΘΣ
⋅Θ⋅
Σ
⋅
=ΘΣ
μ
μ
μ
(10)
It is easy to see that MLE satisfy the following
equations:
(
)
0)(
1
1
=−⋅
∑
=
K
i
ii
XaXtE
K
(11)
(
)
∑
=
−⋅−⋅=Σ
K
i
iTii
XaXaXtE
K
1
)()(
1
ˆ
(12)
(
)
∑
=
−⋅−⋅=Θ
K
i
iT
XaatE
K
1
)
ˆ
()
ˆ
(
1
ˆ
μμ
(13)
1
0
1
1
2
1
ˆ
ˆ
1
ˆ
ln( )
2
d
i
K
i
i
K
i
b
b
E
AX
−
=
=
⋅
⋅
+
=
⎛⎞
⋅
⎜⎟
⎝⎠
∑
∑
(14)
where
,1)
ˆ
(
ˆ
)
ˆ
()(
ˆ
)(
ˆ
11
+−⋅Θ⋅−+−⋅Σ⋅−=
−−
μμ aaaXaXA
TiTi
and conditional expectation is taken for
b
ˆ
,
ˆ
,
ˆ
,
ˆ
ΘΣ μ
.
3 MONTE – CARLO MARKOV
CHAIN
Now it is convenient to calculate the estimates of
parameters by an iterative stochastic optimization
method, starting from some initial values.
Let us consider the application of the Monte –
Carlo Markov chain to implement the method
proposed. Say, random variables and vectors are
generated:
,
0if,
0if,
),,0(N~),
2
(Gamma~
⎪
⎩
⎪
⎨
⎧
<⋅−
≥⋅+
=Θ
jjk
jjk
jkj
k
j
q
q
G
b
B
ηημ
ηημ
η
where
k
Nj ,,2,1,0 K=
,
k
N
is the Monte – Carlo sample
size at the
th
k
step,
K,2,1,0
=
k
, and
0000
,,, bΘΣ
μ
are
some initial approximations. Then
∑
=
+
+=
K
i
ki
ki
kk
P
M
K
1
,
,
1
1
μμ
(15)
∑
=
+
=Σ
K
i
ki
ki
k
P
S
K
1
,
,
1
1
(16)
∑
=
+
=Θ
K
i
ki
ki
k
P
T
K
1
,
,
1
1
(17)
∑
−
=
+
+
+
⋅
⋅=
1
0
1
1
1
2
11
d
i
k
k
k
b
i
h
b
(18)
where the Monte – Carlo estimators are as follows:
∑
=
Σ=
k
N
j
kjj
i
k
ki
BGXf
N
P
1
,
),,,(
1
(19)
()
∑
=
Σ=
k
N
j
kjj
i
k
ki
BGXf
N
P
1
2
,
),,,(
1
1
(20)
()
∑
=
Σ⋅⋅−=
k
N
j
kjj
i
jj
i
k
ki
BGXfBGX
N
M
1
,
),,,(
1
(21)
()() ),,,(
1
1
, kjj
i
j
N
j
T
j
i
j
i
k
ki
BGXfBGXGX
N
S
k
Σ⋅⋅−⋅−=
∑
=
(22)
()()
,
1
1
(,,,)
k
N
T
i
ik jk jk j jjk
k
j
TGGBfXGB
N
μμ
=
=
−⋅− ⋅⋅ Σ
∑
(23)
MAXIMUM LIKELIHOOD ESTIMATION OF MULTIVARIATE SKEW T-DISTRIBUTION
201

∑
=
Σ⋅=
k
N
j
kjj
i
k
k
ki
BGXfA
N
B
1
,
),,,()ln(
1
(24)
()
∑
=
Σ⋅=
k
N
j
kjj
i
k
k
ki
BGXfA
N
B
1
2
,
),,,()ln(
1
1
(25)
() ()
∑∑∑
===
===
K
i
ki
ki
k
k
K
i
ki
ki
k
K
i
ki
ki
k
P
B
K
N
V
P
P
K
Q
P
B
K
h
1
2
,
,
1
2
,
,
1
,
,
1
,
1
1
,
1
(26)
Next, the estimate of the log – likelihood
function (4) is obtained using the Monte – Carlo
estimate (19):
()
∑
=
−=
K
i
kik
PL
1
,
ln
(27)
The 95% confidence interval of the estimate of
the log – likelihood function might also be estimated
by the Monte – Carlo method:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⋅
⋅+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⋅
⋅−
∑∑
==
K
i
ki
kki
k
k
K
i
ki
kki
k
k
P
NP
N
L
P
NP
N
L
1
2
,
,
1
2
,
,
1
2
2
,1
2
2
(28)
where
() .),,,(
1
2
1
2
,
∑
=
Σ=
k
N
j
kjj
i
k
ki
BGXf
N
P
As it follows from equations derived (15) – (18),
the Monte – Carlo chain can be terminated at the
th
k
step, if difference between estimates of two current
steps differs insignificantly:
kkkkkkkk
bb ≈Θ≈ΘΣ≈Σ≈
++++ 1111
,,,
μ
μ
(29)
and, besides, Monte – Carlo estimates are presented
with an admissible confidence interval. Note, since
estimators (19) – (26) are averages of a large number
of identically distributed random variables, their
distribution is approximated, using CLT. Hence, the
statistical criteria about the equality of sampling
mean and covariance matrices to the given vector or
matrices can be used for testing termination
condition (29). It is more convenient to test
hypothesis
kk
hh ≈
+1
instead of
kk
bb ≈
+1
, using the test
for comparison of means from two populations with
the same variance. Thus, the hypothesis on the
termination condition is rejected, if
()()()
()
() () () ]
()
p
kk
kk
kkkk
kkk
T
kk
k
k
k
k
k
k
Z
hV
hh
KNd
Q
K
H
,
2
1
2
1
1
1
1
1
1
1
1
11
2SPSP
lnln
α
μμμμ
>
−
−
⋅⋅+⋅−Θ⋅Θ+Σ⋅Σ+
+−⋅Σ⋅−
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Θ
Θ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Σ
Σ
−⋅=
+
+
−
+
−
+
+
−
+
++
(30)
where
p
Z
, α
is the quantile of
2
χ
distribution with
1)2( ++⋅= ddp
degrees of freedom,
α
is the
significance level.
Note that there is no great necessity to estimate
the likelihood function with a high accuracy on
starting the optimization, because then it is enough
to evaluate only an approximate direction, leading to
its maximum. The next rule of sample size
regulation is implemented; in order large samples
would be taken only at the moment of making the
decision on termination of the Monte – Carlo
Markov chain:
k
k
p
k
H
N
ZN ⋅≥
+
,
1
β
(31)
where
β
is the significance level (Sakalauskas,
2000).
4 NUMERICAL EXAMPLE
The random
),,,( bST
Θ
Σ
μ
sample with
100=K
has
been simulated to explore the approach developed.
The above computational scheme has been used
satisfactorily in numerical work with the following
model data:
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=Θ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=Σ===
55.286.0
86.067.3
,
9.227.0
27.061.1
,21,5,2
μ bd
(32)
The Monte – Carlo Markov chain of 100
estimators (15) – (29) has been computed with the
following initial data:
.5.1,5.1,5.1,5.1
0000
bb ⋅=Θ⋅=ΘΣ⋅=Σ⋅= μμ
The changes of the log – likelihood function
estimate (27), termination statistics (30), sample size
(31) and the length of the confidence interval (28)
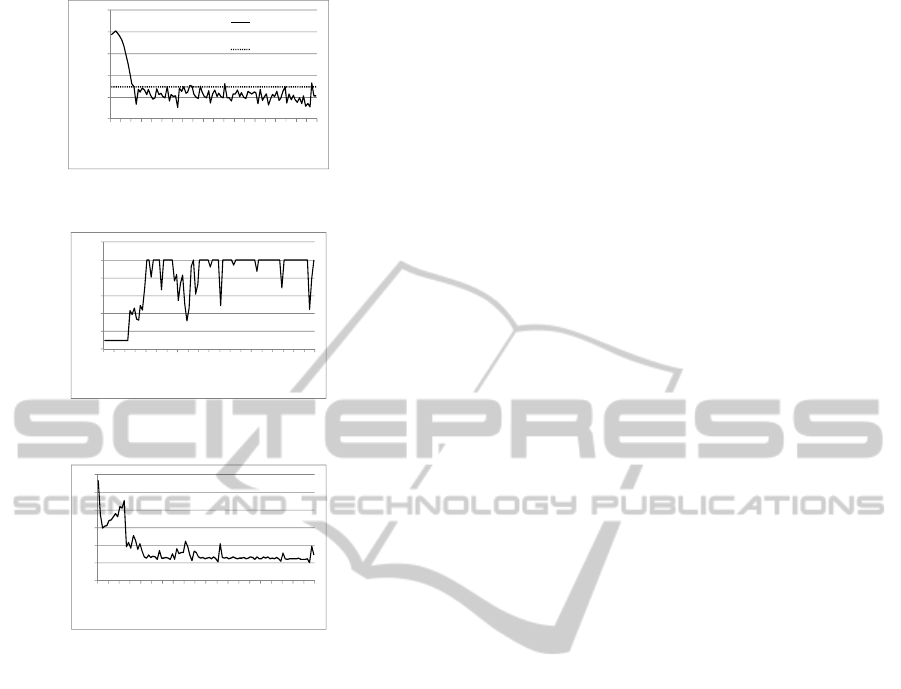
are depicted in Figures 1 – 4. As we see in Figure 1,
the log – likelihood function is decreasing until the
zone of possible solution is achieved.
Correspondingly, the termination criteria in Figure 2
are decreasing too, until the critical value of
termination is achieved. The sample size in Figure 3
is changed so that it was small starting the chain and
increased in the zone of possible solution. To avoid
very small or very large sample sizes, the following
limits were applied:
5000500 ≤≤
k
N
.The length of
the confidence interval in Figure 4 and the error of
estimates decreased as well. The termination
conditions started to be valid at
33=k
.
270
290
310
330
350
370
390
5 152535455565758595
k
Figure 1: Log – likelihood function.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
202

1
10
100
1000
10000
100000
5 152535455565758595
k
test
critical value
Figure 2: Termination test.
0
1000
2000
3000
4000
5000
6000
5 152535455565758595
k
Figure 3: Sample size
k
N
.

0
0,4
0,8
1,2
1,6
2
2,4
5 152535455565758595
k
Figure 4: Confidence interval.
The maximum likelihood estimates (11) – (14),
obtained from this sample by means of the
subroutine Minimize () of MathCAD, are as
follows:
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=Θ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=Σ==
52.1475.0
475.035.2
ˆ
,
86.2708.0
708.091.1
ˆ
,08.295.0
ˆ
,9.3
ˆ
μ b
(33)
5 CONCLUSIONS
Stochastic optimization approach by the Monte –
Carlo Markov Chain (MCMC) method for
estimation of the skew t – distribution has been
developed in the paper. It distinguishes by adaptive
regulation of Monte – Carlo sample size and
treatment of the simulation error in the statistical
manner. Furthermore, the computer example with
test data have illustrated that numerical properties of
the method correspond to the theoretical model.
REFERENCES
Azzalini, A. and Capitanio, A. (2003). Distributions
Generated by Perturbation of Symmetry with
Emphasis on a Multivariate Skew t Distribution.
Journal of the Royal Statistical Society: Series B
(Statistical Methodology), 65, 367 – 389.
Azzalini, A. and Genton, M. G. (2008). Robust Likelihood
Methods Based on the Skew – t and Related
Distributions. International Statistical Review, 76 (1),
106 – 129.
Cabral, C. R. B., Bolfarine, H. and Pereira, J. R. G.
(2008). Bayesian Density Estimation using Skew
Student-t-normal Mixtures. Computational Statistics
and Data Analysis, 52 (12), 5075-5090.
Kim, H. M. and Mallick B. K. (2003). Moments of
Random Vectors with Skew t Distribution and their
Quadratic Forms. Statistics & Probability Letters, 63,
417–423.
Panagiotelis, A. and Smith, M. (2008). Bayesian Density
Forecasting of Intraday Electricity Prices using
Multivariate Skew t Distributions. International
Journal of Forecasting, 24, 710–727.
Rubinstein, R. Y. and Kroese, D. P. (2007). Simulation
and the Monte Carlo Method (2nd ed.). New York:
Wiley.
Sakalauskas, L. (2000). Nonlinear Stochastic Optimization
by Monte-Carlo Estimators. Informatica, 11 (4), 455-
468.
Spall, J. C. (2003). Introduction to Stochastic Search and
Optimization: Estimation, Simulation, and Control.
New York: Wiley.
MAXIMUM LIKELIHOOD ESTIMATION OF MULTIVARIATE SKEW T-DISTRIBUTION
203