
ON ORDER EQUIVALENCES BETWEEN DISTANCE
AND SIMILARITY MEASURES ON SEQUENCES AND TREES
Martin Emms and Hector-Hugo Franco-Penya
School of Computer Science and Statistics, Trinity College, Dublin, Ireland
Keywords:
Similarity, Distance, Tree, Sequence.
Abstract:
Both ’distance’ and ’similarity’ measures have been proposed for the comparison of sequences and for the
comparison of trees, based on scoring mappings, and the paper concerns the equivalence or otherwise of these.
These measures are usually parameterised by an atomic ’cost’ table, defining label-dependent values for swaps,
deletions and insertions. We look at the question of whether orderings induced by a ’distance’ measure, with
some cost-table, can be dualized by a ’similarity’ measure, with some other cost-table, and vice-versa. Three
kinds of orderings are considered: alignment-orderings, for fixed source S and target T, neighbour-orderings,
where for a fixed S, varying candidate neighbours T
i
are ranked, and pair-orderings, where for varying S
i
,
and varying T
j
, the pairings hS
i
,T
j
i are ranked. We show that (1) alignment-orderings by distance can be
dualized by similarity, and vice-versa; (2) neigbour-ordering and pair-ordering by distance can be dualized by
similarity; (3) neighbour-ordering and pair-ordering by similarity can sometimes not be dualized by distance.
A consequence of this is that there are categorisation and hierarchical clustering outcomes which can be
achieved via similarity but not via distance.
1 TREE DISTANCE AND
SIMILARITY
In many pattern-recognition scenarios the data either
takes the form of, or can be encoded as, sequences or
trees. Accordingly, there has been much work on the
definition, implementation and deployment of mea-
sures for the comparison of sequences and for the
comparison of trees.
These measures are sometimes described as ’dis-
tances’ and sometimes as ’similarities’. We are con-
cerned in what follows in first distinguishing between
these, and then with the question whether orderings
induced by a ’distance’ measure can be dualized by
a ’similarity’ measure, and vice-versa. To some ex-
tent this can be seen as applying the same kind of
analysis to sequence and tree comparison measures
as has been applied to set and vector comparison mea-
sures (Batagelj and Bren, 1995; Omhover et al., 2005;
Lesot and Rifqi, 2010).
From statements such as the following
To compare RNA structures, we need a score
system, or alternatively a distance, which
measures the similarity (or the difference) be-
tween the structures. These two versions of
the problem score and distance are equivalent.
(Herrbach et al., 2006)
which are not uncommon in the literature (Alves
et al., 2002; Kondrak, 2003; Bose and van der Aalst,
2009), it would be easy to gain the impression that
similarity and distance (on sequences and trees) are
straightforwardly interchangeable notions. In sec-
tion 1.1 several distinct kinds of equivalence are de-
fined. Sections 2, 3.1 and 3.2 then show that while
some kinds of equivalence hold, others do not.
To begin we need to clarify what we will mean
by ’distance’ and ’similarity’ on sequences and trees.
Because sequences can be encoded as vertical trees it
suffices to give definitions for trees. Tai first proposed
a tree-distance measure (Tai, 1979). Where S and T
are ordered, labelled trees, a Tai mapping α : S 7→ T is
a partial, 1-to-1 function from the nodes of S into the
nodes of T, which respects left-to-right order and an-
cestry
1
. For the purpose of assigning a score to such
a mapping it is convenient to identify three sets:
M the (i, j) ∈ α: the ’matches’ and ’swaps’
D the i ∈ S s.t. ∀ j ∈ T,(i, j) 6∈ α: the ’deletions’
I the j ∈ T s.t. ∀i ∈ S,(i, j) 6∈ α: the ’insertions’
Thus M just is the mapping, as a set of node pairs, and
1
So if (i, j) and (i
′
, j
′
) are in the mapping then (T1)
le ft(i,i
′
) iff left( j, j
′
) and (T2) anc(i,i
′
) iff anc( j, j
′
).
15
Emms M. and Franco-Penya H. (2012).
ON ORDER EQUIVALENCES BETWEEN DISTANCE AND SIMILARITY MEASURES ON SEQUENCES AND TREES.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 15-24
DOI: 10.5220/0003712500150024
Copyright
c
SciTePress
D and I just the remaining nodes of S and T which
are not ’touched’ by the mapping. Let (.)
γ
give the
label of a node and let C
∆
be a ’cost’ table, indexed
by {λ} ∪ Σ, where Σ is the alphabet of labels, which
assigns ’costs’ to M , D and I according to
2
:
for (i, j) ∈ M cost is C
∆
(i
γ
, j
γ
)
for i ∈ D cost is C
∆
(i
γ
,λ)
for j ∈ I cost is C
∆
(λ, j
γ
)
Where α : S 7→ T is any mapping from S to T, define
∆(α : S 7→ T) by
Definition 1. (’Distance’ Scoring of an Alignment).
∆(α : S 7→ T) =
∑
(i, j)∈M
C
∆
(i
γ
, j
γ
) +
∑
i∈D
C
∆
(i
γ
,λ) +
∑
j∈I
C
∆
(λ, j
γ
)
From this costing of alignments, a ’distance’ score on
tree pairs is defined by minimization:
Definition 2. (’Distance’ Scoring of a Tree Pair). The
Tree- or Tai-distance ∆(S,T) between two trees S and
T is the minimum value of ∆(α : S 7→ T) over possible
Tai-mappings from S to T, relative to a chosen cost
table C
∆
.
There is an illustration of the definitions in Figure 1
a
a
ba b
b
c
a b
b
a
b
With C
∆
(x,λ) =
C
∆
(λ,x) = 1,
C
∆
(x,x) = 0, C
∆
(x,y) = 1
for x 6= y, the alignment
has score ∆(α) = 3 and
this is minimal for the
given C
∆
Figure 1: An illustration of tree distance.
∆(S, T) can be computed by the algorithm of (Zhang
and Shasha, 1989). Sequences can be encoded as ver-
tical trees, and on this domain of trees the tree dis-
tance coincides with a well known comparison mea-
sure on sequences, the (alphabet-weighted) string edit
distance (Wagner and Fischer, 1974; Gusfield, 1997).
We have formulated the definition
3
in terms of
costs applied to mappings which respect tree-ordering
properties. In contrast to this declarative perspective,
there is procedural definition via the notion of an edit-
script of atomic operations transforming S to T in a
succession of stages. For both sequences and trees
the mapping-based and script-based notions coincide
2
Note in this general setting even a pairing of two nodes
with identical labels can in principal make a non-zero cost
contribution.
3
The literature contains quite a number of inequivalent
notins, all referred to as ’tree distance’; in this article Defi-
nition 2 will be understood to define the term.
(Wagner and Fischer, 1974; Tai, 1979; Kuboyama,
2007) and so we omit further details of the definition
via edit-scripts.
While the correctness of the Tai ’distance’ al-
gorithm (Zhang and Shasha, 1989) – ie. that it
truly finds the minimal value of ∆(α : S 7→ T) given
cost-table C
∆
– does not require the cost-table C
∆
to satisfy any particular properties, some settings of
C
∆
clearly make little sense. The combination of
deletion/insertion cost-entries which are negative –
C
∆
(x,λ) < 0, C
∆
(λ,y) < 0 – with swap/match cost en-
tries which are not negative givesthe counter-intuitive
effect that a supertree of S is ’closer’ – in the sense of
having a lower ∆ score – to S than S itself
4
. This is a
rationale for the following non-negativity assumption
∀x,y ∈ Σ(C
∆
(x,y) ≥ 0,C
∆
(x,λ) ≥ 0,C
∆
(λ,y) ≥ 0)
(1)
which is a pretty universal assumption, and from
which it follows that ∆(S,T) ≥ 0, giving a minimum
consistency with the every day notion of ’distance’. In
what follows we will confine attention to ’distance’ ∆
based on a table C
∆
which satisfies at least (1).
When the cost-table C
∆
(x,y) is constrained more
strictly than this to satisfy all the conditions of a
distance-metric, then it is well known that ∆(S,T)
will also be a distance-metric. Whether such further
restriction is desirable is moot: in so-called stochas-
tic variants (Ristad and Yianilos, 1998; Bernard et al.,
2008; Emms, 2010), in which the entries in C
∆
are
interpreted as negated logs of probabilities, these ad-
ditional distance-metric assumptions are not fulfilled.
In this article we shall only assume the cost-table C
∆
satisfies the non-negativity requiremnt of (1).
Turning now to ’similarity’, rather than approach
the problem of comparison by minimizing accumu-
lated costs assigned to an alignment, a widely fol-
lowed alternative, especially for sequence compari-
son, has been to maximize a score assigned to an
alignment, with swaps/matches rewarded, and dele-
tions/insertions punished.
Let C
Θ
be a ’similarity’ table, again indexed by
{λ} ∪ Σ, where Σ is the alphabet of labels, and where
α : S 7→ T is any mapping from S to T, and then let
Θ(α : S 7→ T) be defined by
Definition 3. (’Similarity’ Scoring of an Alignment).
Θ(α : S 7→ T) =
∑
(i, j)∈M
C
Θ
(i
γ
, j
γ
) −
∑
i∈D
C
Θ
(i
γ
,λ) −
∑
j∈I
C
Θ
(λ, j
γ
)
From this costing of alignments, a ’similarity’ score
on tree pairs is defined by maximisation:
4
Or a subtree.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
16

Definition 4. (’Similarity’ Scoring of a Tree Pair).
The Tree- or Tai-similarity Θ(S,T) between two trees
S and T is the maximum value of Θ(α : S 7→ T) over
possible Tai-mappings from S to T, relative to a cho-
sen cost table C
Θ
Applied to the same example as shown in Fig-
ure 1, with C
Θ
(x,λ) = C
Θ
(λ,x) = 0, C
Θ
(x,x) = 2,
C
∆
(x,y) = 0 for x 6= y, the shown alignment has score
Θ(α) = 9, which is maximal for the givenC
Θ
.
Θ(S, T) can be computed via a simple modifica-
tion of the algorithm of (Zhang and Shasha, 1989).
Again on the domain of vertical trees this coincides
with a well known approach to sequence comparison,
the (alphabet-weighted) string similarity (Smith and
Waterman, 1981; Gusfield, 1997).
As with ∆, while the correctness of the algorithm
for Θ is not dependent on any assumptions about
the cost-table C
Θ
, some settings of C
Θ
make little
sense. Given the formulation in (3), which subtracts
the contribution from deletions and insertions, a set-
ting where deletion/insertion cost entries are negative
– C
Θ
(x,λ) < 0, C
Θ
(λ,x) < 0 – gives the counter-
intuitive effect that a supertree of S would be more
’similar’ – in the sense of higher Θ score – to S than
S itself. This gives a rationale for the nearly univer-
sal assumption of non-negativedeletion/insertions en-
tries in C
Θ
:
∀x,y ∈ Σ(C
Θ
(x,λ) ≥ 0,C
Θ
(λ,y) ≥ 0) (2)
In what follows we will confine attention always
to ’similarity’ Θ based on a table C
Θ
satisfying (2)
5
.
For the C
Θ
-entries which are not deletions or inser-
tions, it is quite common in biological sequence com-
parison to have both positive and negative entries. In
contrast to the notion of a distance-metric, the notion
of a set of axioms for a similarity Θ is less well es-
tablished. (Chen et al., 2009) have recently made a
proposal concerning this (see section 5).
To reiterate, for the purposes of this discussion a
tree ’distance’ measure will imply a cost-tableC
∆
, sat-
isfying (1), used in accordance to definitions 1 and 2
to score alignments and tree pairs. A tree ’similarity’
measure measure will imply a cost-table C
Θ
, satisfy-
ing (2), used in accordance to definitions 3 and 4 to
score alignments and tree pairs. This is sufficient to
distinguish the ’distance’ approach from the ’similar-
ity’ approach in an intuitive way without commiting
to any further axioms.
5
While Definition 3 formulates Θ with dele-
tion/insertion contributions subtracted, as is often done
(Smith and Waterman, 1981; Stojmirovic and Yu, 2009),
an alternative formulation has these treated additively
(Gusfield, 1997). With the additive formulation, the
same consideration suggests making deletion/insertions
non-positive.
1.1 Order-equivalence Notions between
Tai Distance and Similarity
Given a ’distance’ ∆ scoring of alignments, it can be
set to work to induce orderings of at least three differ-
ent kinds entities
Alignment Ordering. Given fixed S, and fixed T,
rank the possible alignments α : S 7→ T by ∆(α :
S 7→ T)
Neighbour Ordering. Given fixed S, and varying
candidate neighbours T
i
, rank the neighbours T
i
by ∆(S,T
i
) – typically used in k-NN classification.
Pair Ordering. Given varying S
i
, and varying T
j
,
rank the pairings hS
i
,T
j
i by ∆(S
i
,T
j
) – typically
used in hierarchical clustering.
Similarly a ’similarity’ Θ scoring of alignments in-
duces orderings of the above kinds of entities. Com-
paring these orderings motivates the following defini-
tion
Definition 5. (A-,N- and P-dual). When the align-
ment orderings induced by a choice of C
∆
(used in ac-
cordance with (1)) and by a choice C
Θ
(used in accor-
dance with (3)) are the reverse of each other, we will
say that C
Θ
is a A-dual of C
∆
. Similarly we will say
we have an N-dual when neighbour ordering is re-
versed, and a P-dual where pair-ordering is reversed.
For example, the following are A-duals in this
sense (proven in section 2):
Example 1.
∆ with
C
∆
(x,λ) = 1
C
∆
(x,x) = 0
C
∆
(x,y) = 1
Θ with
C
Θ
(x,λ) = 0
C
Θ
(x,x) = 2
C
Θ
(x,y) = 1
Example 2.
∆ with
C
∆
(x,λ) = 0.5
C
∆
(x,x) = 0
C
∆
(x,y) = 0.5
Θ with
C
Θ
(x,λ) = 0
C
Θ
(x,x) = 1
C
Θ
(x,y) = 0.5
A natural question that presents itself then is
whether for every choice ofC
∆
, there is a choice ofC
Θ
which is a A-dual, N-dual or P-dual, and vice-versa.
More precisely there are the following
Order-relating Conjectures.
A-duality
(i) ∀C
∆
∃C
Θ
(C
∆
and C
Θ
are A-duals)
(ii) ∀C
Θ
∃C
∆
(C
∆
and C
Θ
are A-duals)
N-duality
(i) ∀C
∆
∃C
Θ
( C
∆
and C
Θ
are N-duals)
(ii) ∀C
Θ
∃C
∆
( C
∆
and C
Θ
are N-duals)
P-duality
(i) ∀C
∆
∃C
Θ
( C
∆
and C
Θ
are P-duals)
(ii) ∀C
Θ
∃C
∆
( C
∆
and C
Θ
are P-duals)
Arguably these notions go to the heart of the
question whether there is really anything that can
be accomplished using an alignment ’distance’ score,
ON ORDER EQUIVALENCES BETWEEN DISTANCE AND SIMILARITY MEASURES ON SEQUENCES AND
TREES
17

which cannot by accomplised via an alignment ’sim-
ilarity’ score, and vice-versa. For example, if it
turns out that all these order conjectures hold, then
any alignment outcome, any categorisation outcome
via k-NN and any hierarchical clustering outcome,
achieved by a particular distance can be replicated by
a similarity, and vice-versa, making the choice merely
a matter of personal taste. On the other hand, if these
duality conjectures do not hold, then there is substan-
tive difference, with the outcomes achievable by dis-
tances and similarities being distinct.
For a number of similarity and distance measures
based on sets and vectors, notions analogous to N-
dual and P-dual have been considered (Batagelj and
Bren, 1995; Omhover et al., 2005; Lesot and Rifqi,
2010), motivated similarly by the question whether
anything which can be accomplished with one or
other such measure can be replicated by another such
measure. It is for example shown there that a particu-
lar Dice measure will rank retrieval results inevitably
the same as a particular Jaccard measure. In the case
of alignment-based measures on sequences and trees,
as far as we are aware, these notions seem not have
been systematically considered and the following sec-
tions endeavour to fill that gap.
2 ALIGNMENT-DUALITY
The following lemma will be useful for considering
the A-duality conjectures above:
Lemma 1. For any C
∆
, and some choice δ such that
0 ≤ δ/2 ≤ min(C
∆
(·,λ),C
∆
(λ,·)) let C
Θ
be defined
according to (i) below. For anyC
Θ
, and choice δ such
that 0 ≤ δ ≥ max(C
Θ
(·,·)) letC
∆
be defined according
to (ii) below.
(i)
C
Θ
(x,λ) = C
∆
(x,λ) − δ/2
C
Θ
(λ,y) = C
∆
(λ,y) − δ/2
C
Θ
(x,y) = δ −C
∆
(x,y)
(ii)
C
∆
(x,λ) = C
Θ
(x,λ) + δ/2
C
∆
(λ,y) = C
Θ
(λ,y) + δ/2
C
∆
(x,y) = δ −C
Θ
(x,y)
then in either case, for any α : S 7→ T
∆(α)+ Θ(α) = δ/2× (
∑
s∈S
(1) +
∑
t∈T
(1)) (3)
Proof of Lemma 1. If defining C
Θ
from C
∆
by (i), by
the choice of δ we have the non-negativity of C
Θ
(x,λ)
and C
Θ
(λ,y). If defining C
∆
from C
Θ
by (ii), by the
choice of δ, we have the non-negativity of all entries
in C
∆
.
Whether defining C
Θ
from C
∆
by (i), or C
∆
from C
Θ
by
(ii), it is straightforward to show
∆(α) + Θ(α) = δ/2× (2|M | + |D| + |I |)
But then (3) follows since
2|M | + |D| + |I | =
∑
s∈S
(1) +
∑
t∈T
(1)
Theorem 2. A-duality (i) and (ii) hold
Proof of Theorem 2. A-duality (i): defineC
Θ
accord-
ing to (i) in Lemma 1. Given the constant summation
property of (3), the ordering on alignments by ∆ must
be the reverse of the ordering by Θ.
A-duality (ii): similarly defineC
∆
accordingto (ii)
in Lemma 1
Example 1 Revisited. The C
Θ
of Example 1 can be
seen as derived from the C
∆
with δ = 2. Table below
shows outcomes for other choices of δ
C
∆
C
Θ
(δ = 2) C
Θ
(δ = 1) C
Θ
(δ = 0)
(x,λ) 1 0 0.5 1
(x,x) 0 2 1 0
(x,y) 1 1 0 -1
As a corollary one can obtain the following con-
cerning how one similarity table can be ’shifted’ to an
equivalent one, and similarly for distance tables.
Corollary 3. (’Shifting’). for any C
Θ
1
, an alignment
equivalent C
Θ
2
can be derived by the conversion (a)
below, and for any C
∆
1
, an alignment equivalent C
∆
2
can be derived by the conversion (b)
(a)
C
Θ
2
(x,λ) = C
Θ
1
(x,λ) − κ/2
C
Θ
2
(λ,y) = C
Θ
1
(λ,y) − κ/2
C
Θ
2
(x,y) = C
Θ
1
(x,y) + κ
(b)
C
∆
2
(x,λ) = C
∆
1
(x,λ) + κ/2
C
∆
2
(λ,y) = C
∆
1
(λ,y) + κ/2
C
∆
2
(x,y) = C
∆
1
+ κ
Proof of Corollorary 3. (a) is the composition of (ii),
for some δ
1
, with (i), for some δ
2
, giving κ = δ
2
− δ
1
.
(b) is the composition (i), for some δ
1
, with (ii), for
some δ
2
, giving κ = δ
2
− δ
1
Example 1 Revisited Again. The three A-dualizing
similarities C
Θ
(δ = 2), C
Θ
(δ = 1) and C
Θ
(δ = 0) de-
rived from the unit-cost distance table using varying
δ in the (i) conversion of Lemma 1 can be seen as re-
lated to each other by the (a) ’shifting’ conversion of
Lemma 3, with κ = −1 each time.
The property of alignment dualizability between dis-
tance and similarity (and vice-versa) expressed above
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
18

in Lemma 1 and Theorem 2 was essentially first
proven for the case of sequence comparison by (Smith
and Waterman, 1981). On the basis of this perhaps it
is tempting to consider the case closed and treat ’dis-
tance’ and ’similarity’ as interchangeable. However,
as noted in Section 1.1, there is more than one kind
of ordering that one might wish to be sure of repli-
cating in switching between distance and similarity,
with N-duality coming to the fore in the context of
k-NN classification, and P-duality coming to the fore
in the context of hierarchical clustering. Section 3.1
considers the N-duality (i) and P-duality (i) order con-
jectures, and Section 3.2 considers the N-duality (ii)
and P-duality (ii) conjectures.
3 NEIGHBOUR AND PAIR
ORDERING
3.1 Distance to Similarity
Having seen that A-duals can always be created in
both directions, attention shifts to N-duals and P-
duals.
The case of using δ = 0 in the (i) conversion of
Lemma 1 from C
∆
to C
Θ
gives non-positive values
for all non-deletion, non-insertion entries in C
Θ
, and
is an especially trivial case of dualizing a distance set-
ting C
∆
, with the effect that Θ(S,T) = −1 × ∆(S,T).
Because of this, this distance-to-similarity conversion
not only makes A-duals, but also N-duals and P-duals.
Theorem 4. N-duality (i) and P-duality(i) hold
Proof of Theorem 4. By choosing δ = 0 in the
(i) conversion of Lemma 1 from C
∆
to C
Θ
, we
have Θ(S,T) = −1× ∆(S,T), and hence Θ(S
1
,T
1
) ≤
Θ(S
2
,T
2
) ⇔ ∆(S
1
,T
1
) ≥ ∆(S
2
,T
2
)
This distance-to-similarity by negation is well
known. On the other hand, concerning similarity-to-
distance, in the (ii) conversionof Lemma 1 fromC
Θ
to
C
∆
, you can only choose δ = 0 if all C
Θ
(x,y) ≤ 0, and
clearly there are many natural settings of C
Θ
where
that is not true.
3.2 Similarity to Distance
The remaining order-equivalence conjectures of sec-
tion 1.1 are N-duality(ii) and P-duality(ii), concern-
ing the similarity-to-distance direction. Of the re-
maining conjectures, P-duality(ii) is stronger than N-
duality(ii). We can fairly easily show P-duality(ii)
does not hold
Theorem 5. P-duality (ii) does not hold, that is, there
are C
Θ
such that there is no C
∆
such that C
Θ
and C
∆
are P-duals.
Proof of Theorem 5. It is clearly possible for C
Θ
to
be such that there is no maximum value for Θ(S,T).
For example for table below:
C
Θ
(a,a) 1
(a,λ) 1
its clear we have Θ(a,a) = 1, Θ(aa,aa) = 2 and in
general Θ(a
n
,a
n
) = n. Let C
Θ
be any table defin-
ing a similarity with no maximum. On the other
hand, for each C
∆
there will be minimum value of
∆(S, T). Suppose some C
∆
is a P-dual to C
Θ
. For
any n let [Θ]
n
(resp. [∆]
n
) be the set of pairs with
similarity (resp. distance) n. If C
∆
is a P-dual to
C
Θ
, there is some bijection between the set of simi-
larity classes { [Θ]
s
} and the set of distances classes
of {[∆]
d
}. Some similarity class [Θ]
s
1
of Θ must cor-
respond to the minimum distance class [∆]
d
0
. Let
[Θ]
s
2
be a higher Θ class than [Θ]
s
1
. It must corre-
spond to some ∆ class [∆]
d
1
distinct from [∆]
d
0
, and
since [∆]
d
0
is the distance-minimum, this must be a
higher distance class. Then for (S
0
,T
0
) ∈ [∆]
d
0
, and
(S
1
,T
1
) ∈ [∆]
d
1
you have ∆(S
0
,T
0
) < ∆(S
1
,T
1
), but
also Θ(S
0
,T
0
) < Θ(S
1
,T
1
). So the supposed dual C
∆
does not reverse the pair-ordering of C
Θ
.
Of the order-relating conjectures of section 1.1 the
only remaining one is N-duality(ii) – that is the ques-
tion whether every neighbour-ordering via some C
Θ
can be replicated by a neighbour ordering via some
C
∆
. We can show that there are neighbour-orderings
by a Tai-similarity which cannot be dualized by any
Tai-distance whose deletion and insertion costs are
symmetric.
Theorem 6. There is C
Θ
such that there is noC
∆
with
C
∆
(x,λ) = C
∆
(λ,x) such that C
Θ
and C
∆
are N-duals
Proof of Theorem 6. Let S = aa, and the set of neigh-
bours be {a,aaa}.
Let C
Θ
(a,a) = x > 0, and C
Θ
(a,λ) = C
Θ
(λ,a) = y >
0.
For (aa,aaa), the alignments with 2,1, and 0 a-
matches haves scores, 2x− y, x− 3y and −5y, respec-
tively, so the alignments maximising Θ are those with
two a-matches, and Θ(aa,aaa) = 2x− y.
For (aa,a), the alignments with 1 and 0 a-matches
have scores x − y and −3y, respectively, so the
alignments maximising Θ have one a-match, and
Θ(aa,a) = x− y.
Consider what is required for the Θ-decreasing
neigbour ordering to be: [aaa, a],
ON ORDER EQUIVALENCES BETWEEN DISTANCE AND SIMILARITY MEASURES ON SEQUENCES AND
TREES
19
Θ(aa,aaa) > Θ(aa,a)
⇔ 2x− y > x− y
⇔ x > 0
So there is a Θ-decreasing neighbour-ordering
[aaa, a].
Let C
∆
(a,a) = x
′
, and C
∆
(a,λ) = C
∆
(λ,a) = y
′
. Note
this assumes symmetric insertion and deletion costs.
For (aa,aaa), the alignments with 2,1, and 0 a-
matches haves scores, 2x
′
+ y
′
, x
′
+ 3y
′
and 5y
′
, re-
spectively. We distinguish two cases (i) 2y
′
< x
′
and
(ii) 2y
′
≥ x
′
.
For case (i), x
′
= 2y
′
+ ε, for some no-zero ε > 0,
and the 2,1,and 0 a-matches scores become 5y
′
+ 2ε,
5y
′
+ ε and 5y
′
, respectively, so taking the minimum,
∆(aa,aaa) = 5y
′
.
For case (ii), y
′
= x
′
/2+κ, for some κ ≥ 0, and the
2,1,and 0 a-matches scores become 2.5x
′
+ κ, 2.5x
′
+
3κ and 2.5x
′
+ 5κ, respectively, and 2-match case is
amongst the minimal cases, so ∆(aaa, aa) = 2.5x
′
+κ.
For (aa,a), the alignments with 1 and 0 a-matches
haves scores, x
′
+ y
′
and 3y
′
respectively. We again
distinguish between cases (i) 2y
′
< x
′
and (ii) 2y
′
≥ x
′
.
For case (i), the 1 and 0 a-matches scores become
3y
′
+ ε and 3y
′
respectively, so taking the minimum,
∆(aa,a) = 3y
′
.
For case (ii), the 1 and 0 a-match scores become
1.5x
′
+ κ and 1.5x
′
+ 3κ respectively, and the 1-match
case is amongst the minimal cases, so ∆(aa, a) =
1.5x
′
+ κ.
Summarising the ∆ possibilities
∆(aa,aaa) ∆(aa,a)
(i)2y
′
< x
′
5y
′
3y
′
(ii)2y
′
≥ x
′
2.5x
′
+ κ 1.5x
′
+ κ
So in neither case (i) nor case (ii) is it possible to
achieve a ∆-ascending neighbour ordering [aaa, a],
which was the Θ-descending neighbour ordering
which was achieved with the assumed C
Θ
.
Remark. If we drop the requirement that the N-
dualizing C
∆
have C
∆
(x,λ) = C
∆
(λ,x), then the ar-
gument does not go through. The Θ-descending
neighbour ordering [aaa,a] can be replicated by
a ∆-ascending neighbour ordering with C
∆
(a,λ) >
C
∆
(λ,a). For most applications of alignment-based
’distances’, such an asymmetric setting of deletion
and insertion costs would be considered unnatural.
4 EMPIRICAL INVESTIGATION
(Lesot and Rifqi, 2010) consider distance and sim-
ilarity measures often used in information retrieval.
These are defined over finite vectors, whose features
are either binary or real-valued. They basically con-
sider the neighbour orderings produced by different
measures. Besides demonstrating absolute equiva-
lence between some measures, between other mea-
sures they empirically determine equivalence degrees,
between 0 and 1, based on the Kendall-tau statistic
for comparing orderings (Kendall, 1945). While their
work concerned comparison measures on vectors, it
is a natural to consider an analogous empirical quan-
tified comparison of distance and similarity orderings
on trees and sequences. Some preliminary findings of
such a study are given below.
The (i) conversion of Lemma 1 converts distance
settings to A-dual similarity settings and one thing to
consider is the degree to which the derived similari-
ties are also N-duals of the distance. Table 1 gives
some distance and similarity settings: the first column
gives the unit-cost settings for ∆ and the columns to
the right give different similarity settings C
Θ
deriv-
able by the (i) conversion of Lemma 1 as δ is varied
through various values.
Table 1: Unit-cost distance setting and several A-dual simi-
larity settings.
dual C
Θ
for varying δ
C
∆
2 1.5 1 0.5 0.2 0.1 0
(x,λ) 1 0 0.25 0.5 0.75 0.9 0.95 1
(x,x) 0 2 1.5 1 0.5 0.2 0.1 0
(x,y) 1 1 0.5 0 -0.5 -0.8 -0.9 -1
An experiment was done to quantify how close the
similarities defined by the varying C
Θ
tables come to
being N-duals for the distance. Using a set of 1334
trees
6
, repeatedly a tree S was chosen, and neighbour
files N
∆
(S) and N
Θ
(S) were computed, with N
∆
(S)
the ordering of the remaining trees by ascending ∆,
and N
Θ
(S) the ordering by descending Θ. N
∆
(S) and
N
Θ
(S) were then compared by the kendall-tau mea-
sure τ (see the Appendix for the definition). For each
δ the average of this τ comparison between the dis-
tance and similarity neighbour files is shown in Fig-
ure 2.
The bottom-left corner, for δ = 0 is the special
case of Lemma 1 which amounts to the well-known
trivial distance-to-similarity conversion, Θ(S,T) =
−1 × ∆(S,T), noted in section 3.1. In this case the
distance and similarity neighbour files are identical.
6
See the Appendix for further details of this data set.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
20
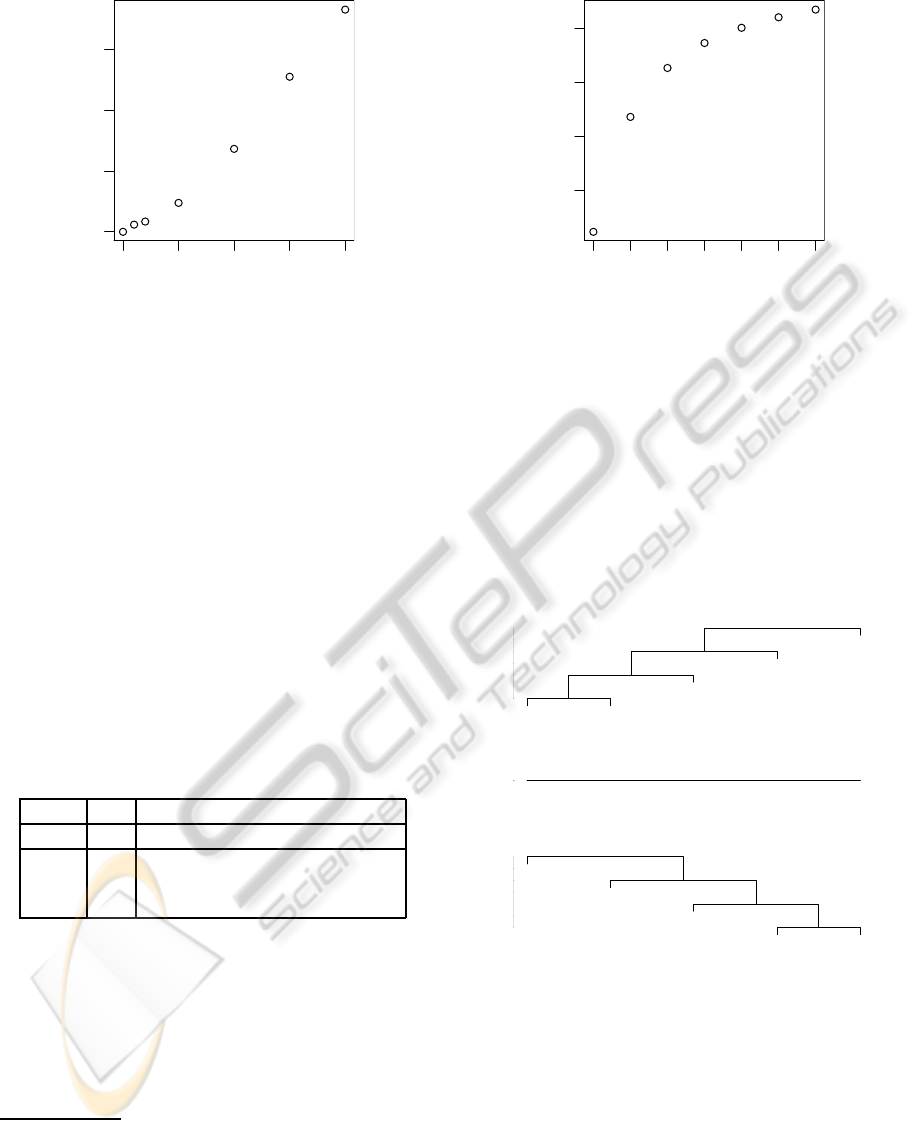
0.0 0.5 1.0 1.5 2.0
0.0 0.2 0.4 0.6
delta
tau
Figure 2: Average Kendall-tau comparison on neighbours
using distance and derived similarities. Distance setting
is first column of Table 1. Similarity settings are further
columns of Table 1 defined by varying δ.
As the graph clearly shows, as δ increases, the neigh-
bour files exhibit progressively greater difference in
ordering, until at δ = 2 the τ score is 0.73, which cor-
responds to a tendency more towards order reversal
than to replication. This experiment shows that al-
though each of these similarity settings is an A-dual
of the simple distance setting, they are not at all equiv-
alent to each other as far as neighbour ordering is con-
cerned.
The (ii) conversion of Lemma 1 converts similar-
ity settings to A-dual distance settings. Table 2 gives
a similarity setting and then several distance settings
derivable by the (ii) conversion as δ is varied through
various values
7
Table 2: A similarity setting and several A-dual distance
settings.
dual C
∆
for varying δ
C
Θ
1 1.5 2 2.5 3 3.5 4
(x,λ) 0.5 1 1.25 1.5 1.75 2 2.25 2.5
(x,x) 1 0 0.5 1 1.5 2 2.5 3
(x,y) 0 1 1.5 2 2.5 3 3.5 4
Figure 3 plots the average τ comparison between
the similarity and distance neighbour files, as δ is var-
ied to give different distances. Again this experiment
shows that although each of the distance settings is an
A-dual of the similarity setting, they are not equiva-
lent to each other as far as neighbour ordering is con-
cerned.
7
The nodes in these experiments have multi-part labels.
Whilst the first experiment treated these simply as identi-
cal or not, for this second experiment, the base-line similar-
ity node label are compared via C
Θ
(x,y) = 1 − ham(x,y),
ham(x,y) is the standard hamming distance. The table thus
shows the extreme values of C
Θ
(x,y) and C
∆
(x,y).
1.0 1.5 2.0 2.5 3.0 3.5 4.0
0.30 0.32 0.34 0.36
delta
tau
Figure 3: Average Kendall-tau comparison on neighbours
using a similarity and derived distances. Similarity setting
is first column of Table 2. Distance settings are further
columns of Table 2 defined by varying δ.
Theorem 5 concerned the non-replicability by dis-
tance of pair-orderings by similarity. To illustrate
this, consider a set of strings {a
5
,a
4
,a
3
,a
2
,a
1
}. A ta-
ble of pair-wise similarities of these was made with
C
Θ
(a,a) = 1,C
Θ
(a,λ) = 1, and used to generate a
single-link clustering, shown as the the uppermost
dendrogram in Figure 4.
i5
i4
i3
i2
i1
sim swap:1 del:1 single
i5
i4
i3
i2
i1
dist swap:0 del:1 single
i5
i4
i3
i2
i1
dist swap:1 del:1 single
Figure 4: Similarity and distance clusterings. The instance
labels i5. . . i1 represesent a
5
...a
1
.
No single-link clustering based on distance repli-
cates this similarity clustering. The middle den-
dogram in Figure 4 is the result with C
∆
(a,a) =
0,C
∆
(a,λ) = 1, with all five shown on the same level
because ∆(a
m
,a
m+1
) = 1. The lowest dendogram in
Figure 4 shows a result with C
∆
(a,a) = 1,C
∆
(a,λ) =
1. The same structure was found holding C
∆
(a,a) =
1, and allowing the deletion/insertion cost to vary be-
tween 0.5 and 5.5 (which are ≥ C
∆
(a,a)) and between
ON ORDER EQUIVALENCES BETWEEN DISTANCE AND SIMILARITY MEASURES ON SEQUENCES AND
TREES
21

0.4 and 0.1 (which are < C
∆
(a,a))
5 DISCUSSION AND
COMPARISONS
In view of the outcomes noted in sections 2, 3.1 and
3.2 concerning the various ordering conjectures we
can say that
• Any hierarchical clustering outcome achieved via
∆ can be replicated via Θ, but not vice-versa.
• Any categorisation outcome using nearest-
neighbours achieved via ∆ can be replicated via
Θ, but not vice-versa.
and in this sense ’similarity’ and ’distance’ compar-
ison measures on sequences and trees are not inter-
changeable.
As far as we are aware this aspect of the choice
between a similarity-based versus a distance-based
comparison measure on sequences or trees has not
been noted before.
There are a number of papers concerning con-
version from a similarity-based sequence compari-
son measure to a distance-based comparison mea-
sure, and particularly one satisfying distance-metric
axioms (Spiro and Macura, 2004; Stojmirovic and Yu,
2009). An aim of these papers is to find techniques for
accelerating so-called range similarity queries, which
are requests to find all neighbours within a similar-
ity threshold N
≤θ
(S) = {T : Θ(S,T) ≥ θ}. To discuss
these papers it will be as well to note the distance-
metric axioms
Definition 6. (Distance Metric). A binary relation ∆
is a distance-metric if it satisfies
D1.∆(S,T) = ∆(T,S)
D2.∆(S,T) ≥ 0
D3.∆(S,V) ≤ ∆(S,T) + ∆(T,V)
D4.∆(S,T) = 0 iff S = T
It is a pseudo-metric if D4. is dropped. It is a
quasi-metric if D1. is droppped
For a distance-metric on sequences there is a way
to use the triangle-inequality to accelerate solution of
a distance range query, N
≤δ
(S) = {T : ∆(S, T) ≤ δ}.
Suppose S is a query, and T
1
is a training-set point
known to be far from S, and that another training-set
point T
2
is knownto be close to T
1
. Intuitively S is also
going to be far from T
2
. More specifically, if ∆ is a
distance-metric, an instance of the triangle-inequality
will be:
∆(S,T
1
) ≤ ∆(T
1
,T
2
) + ∆(T
2
,S) (4)
via which ∆(T
2
,S) is bounded below by ∆(S, T
1
) −
∆(T
1
,T
2
). So if T
1
has already been excluded from a
distance neigbhourhood, T
2
can be also immediately
excluded if ∆(S,T
1
) − ∆(T
1
,T
2
) exceeds the thresh-
old.
Most biologicalsequence comparison is done with
similarity not distance and the concern of (Spiro and
Macura, 2004) is to find a corresponding means of ac-
celerating similarity range queries. In terms of the no-
tations used here, they essentially propose the follow-
ing conversion from similarity to distance cost-table
∀x,y ∈ Σ (C
∆
(x,y) = C
Θ
(x,x) +C
Θ
(y,y) − 2C
Θ
(x,y))
∀x ∈ Σ (C
∆
(x,λ) = C
Θ
(x,λ))
∀y ∈ Σ (C
∆
(λ,x) = C
Θ
(λ,x))
and they prove that, under some conditions imposed
on C
Θ
, the corresponding ∆ will satisfy all the condi-
tions of a distance-metric, in particular satisfying the
triangle-inequality. and that the relation between Θ
and ∆ is then
∆(X,Y) = Θ(X,X) + Θ(Y,Y) − 2Θ(X,Y) (5)
Substitution of (5) into the triangle-inequality and
some re-arrangement gives that Θ(T
2
,S) is bounded
above by Θ(S,T
1
) + Θ(T
2
,T
2
) − Θ(T
1
,T
2
), giving a
means for rapid exclusion of T
2
from a similarity
neigbhourhood.
Beside the fact that equation (5) relating Θ and ∆
holds only under particular assumptions concerning
C
Θ
, more importantly the obtained relationship in (5)
is not sought in the context of deriving a P-dual or
N-dual distance ∆ from a given similarity Θ, and in
fact (5) does not do this. Thus while Spiro et al do
provide a conversion from a similarity to a distance, it
addresses concerns somewhat orthogonal to those of
this paper.
(Stojmirovic and Yu, 2009) is a paper with similar
concerns to (Spiro and Macura, 2004). In terms of
the notations used here, they propose the following
conversion from similarity to distance cost-table:
∀x,y ∈ Σ (C
∆
(x,y) = C
Θ
(x,x) −C
Θ
(x,y))
∀x ∈ Σ (C
∆
(x,λ) = C
Θ
(x,x) +C
Θ
(x,λ))
∀y ∈ Σ (C
∆
(λ,x) = C
Θ
(λ,x))
and prove, under some assumptions concerning C
Θ
,
that the then derived ’distance’ is a quasi-metric and
that the relationship between ∆ and Θ is then:
∆(S, T) = Θ(S, S) − Θ(S,T) (6)
Though not a distance-metric – it is asymmetric
– it does satisfy the triangle-inequality ∆(X, Z) ≤
∆(X,Y) + ∆(Y,Z), and substituting (6) into the
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
22

triangle-inquality and re-arranging again gives an up-
per bound which might be used to accelerate a simi-
larity range query: Θ(S,T
2
) ≤ Θ(S,T
1
) + Θ(T
2
,T
2
) −
Θ(T
2
,T
1
).
Though again this similarity to distance conver-
sion is not sought in the context of finding P- or N-
duals, Stojmirov et al’s equation in (6) does make the
derived distance an N-dual of the similarity. This is
not, however, inconsistent with the example in sec-
tion 3.2 of a similarity with no N-dualizing distance.
Stojmirov et al’s conversion generates asymmetric in-
sertion and deletion entries in the distance cost-table
C
∆
, whereas the proof in section 3.2 concerned the
impossibily of a N-dualizing distance with symmetric
insertion and deletion entries.
Our findings on the various order-relating conjec-
tures concern notions with specific, though widely
used, definitions (Defs.1, 2, 3 and 4). There are other
closely related notions, and the corresponding ques-
tions concerning these have not been addressed. One
variant is stochastic: in a stochastic similarity, proba-
bilities are assigned to aspects of a mapping and mul-
tiplied. We conjecture that these will be A-, N- and
P-dualisable to distance. This is because, under a log-
arithmic mapping, it seems such stochastic variants
can be exactly simulated by a similarity as we have
defined it. In the resulting table, all C
Θ
(x,y) ≤ 0,
allowing the (ii) conversion of Lemma 1 to define a
C
∆
choosing δ = 0. There are also normalised vari-
ants, which we have not considered. Throwing the net
very much more widely, (Chen et al., 2009) study re-
lationships between distance and similarity measures,
in a very general setting, not restricted to measures
based on sequence or tree alignment. Parallel to the
well-known axioms of a distance-measure, they pro-
pose a set of similarity axioms, and they define con-
versions from similarity to distance and in the other
direction, showing that the derived score satisfies the
relevant axioms if the score that is input to the conver-
sion does. Their work, however, does not address the
question whether the conversions give N- or P-duals,
that is whether they preserve relevant orderings.
Concerning directions for further work, the em-
pirical investigation in section 4 was quite prelimi-
nary. For the Kendall-tau comparison of distance and
similarity neighbourhoods, we looked at just one par-
ticular baseline distance and one particular baseline
similarity, and compared only to A-duals as given by
Lemma 1, so clearly there are other possibilities one
could consider here. One is Spiro and Macura’s re-
lation in (5). The Appendix notes some further A-
dualizing conversions, from distannce to similarity
and from similarity to distance, which might be con-
sidered. It is also the case that we applied the Kendall-
tau comparison to full rankings, and it would be of in-
terest to look also at top-k ranking, as has been done
for vector- and set-based measures (Lesot and Rifqi,
2010).
ACKNOWLEDGEMENTS
This research is supported by the Science Foundation
Ireland (Grant 07/CE/I1142) as part of the Centre for
Next Generation Localisation (www.cngl.ie) at Trin-
ity College Dublin.
REFERENCES
Alves, C. E. R., C´aceres, E. N., and Dehne, F. (2002). Paral-
lel dynamic programming for solving the string edit-
ing problem on a cgm/bsp. In Proceedings of the four-
teenth annual ACM symposium on Parallel algorithms
and architectures, SPAA ’02, pages 275–281. ACM.
Batagelj, V. and Bren, M. (1995). Comparing resemblance
measures. Journal of Classification, 12(1):73–90.
Bernard, M., Boyer, L., Habrard, A., and Sebban, M.
(2008). Learning probabilistic models of tree edit dis-
tance. Pattern Recogn., 41(8):2611–2629.
Bose, R. P. J. C. and van der Aalst, W. M. P. (2009). Con-
text aware trace clustering: Towards improving pro-
cess mining results. In SAIM International Confer-
ence on Data Mining, SDM, pages 401–412.
Chen, S., Ma, B., and Zhang, K. (2009). On the similarity
metric and the distance metric. Theoretical Computer
Science, 410(24-25):2365 – 2376.
Emms, M. (2010). Trainable tree distance and an applica-
tion to question categorisation. In KONVENS 2010.
Emms, M. and Franco-Penya, H. (2011). Data-
set used in Kendall-Tau experiments
www.scss.tcd.ie/Martin.Emms/SimVsDistData.
Gusfield, D. (1997). Algorithms on strings, trees, and se-
quences. Cambridge Univ. Press.
Haji, J., Ciaramita, M., Johansson, R., Kawahara, D., Mey-
ers, A., Nivre, J., Surdeanu, M., Xue, N., and Zhang,
Y. (2009). The conll-2009 shared task: Syntactic and
semantic dependencies in multiple languages. In Pro-
ceedings of the 13th Conference on Computational
Natural Language Learning (CoNLL-2009).
Herrbach, C., Denise, A., Dulucq, S., and Touzet, H. (2006).
Alignment of rna secondary structures using a full set
of operations. Technical Report 145, LRI.
Kendall, M. G. (1945). The treatment of ties in ranking
problems. Biometrika, 33(3):239–251.
Kondrak, G. (2003). Phonetic alignment and similarity.
Computers and the Humanities, 37.
Kuboyama, T. (2007). Matching and Learning in Trees.
PhD thesis, Graduate School of Engineering, Univer-
sity of Tokyo.
Lesot, M.-J. and Rifqi, M. (2010). Order-based equiva-
lence degrees for similarity and distance measures.
In Proceedings of the Computational intelligence
ON ORDER EQUIVALENCES BETWEEN DISTANCE AND SIMILARITY MEASURES ON SEQUENCES AND
TREES
23

for knowledge-based systems design, and 13th inter-
national conference on Information processing and
management of uncertainty, IPMU’10, pages 19–28,
Berlin, Heidelberg. Springer-Verlag.
Omhover, J.-F., Rifqi, M., and Detyniecki, M. (2005).
Ranking invariance based on similarity measures in
document retrieval. In Adaptive Multimedia Retrieval,
pages 55–64.
Ristad, E. S. and Yianilos, P. N. (1998). Learning string edit
distance. IEEE Transactions on Pattern Recognition
and Machine Intelligence, 20(5):522–532.
Smith, T. F. and Waterman, M. S. (1981). Comparison
of biosequences. Advances in Applied Mathematics,
2(4):482 – 489.
Spiro, P. A. and Macura, N. (2004). A local alignment
metric for accelerating biosequence database search.
Journal of Computational Biology, 11(1):61–82.
Stojmirovic, A. and Yu, Y.-K. (2009). Geometric aspects of
biological sequence comparison. Journal of Compu-
tational Biology, 16:579–610.
Tai, K.-C. (1979). The tree-to-tree correction problem.
Journal of the ACM (JACM), 26(3):433.
Wagner, R. A. and Fischer, M. J. (1974). The string-to-
string correction problem. Journal of the Association
for Computing Machinery, 21(1):168–173.
Zhang, K. and Shasha, D. (1989). Simple fast algorithms for
the editing distance between trees and related prob-
lems. SIAM Journal of Computing, 18:1245–1262.
APPENDIX
Proof of Alignment Sum Property from Lemma 1.
In the proof of Lemma 1 it was claimed with C
∆
and
C
Θ
related according to the (i) or (ii) conversions that
for any alignment α, ∆(α) + Θ(α) = δ/2 × (2|M | +
|D| + |I |). This is proven as follows.
If defining C
Θ
from C
∆
by (i), for Θ(α) we have:
∑
(i, j)∈M
[δ−C
∆
(i, j)] −
∑
i∈D
[C
∆
(i,λ) − δ/2]
−
∑
j∈I
[C
∆
(λ, j) − δ/2)
= δ(|M | +
|D|
2
+
|I |
2
)
−
∑
(i, j)∈M
[C
∆
(i, j)] −
∑
i∈D
[C
∆
(i,λ)] −
∑
j∈I
[C
∆
(λ, j)]
=
δ
2
(2|M | + |D| + |I |) − ∆(α)
If defining C
∆
from C
Θ
by (ii), for ∆(α) we have
∑
(i, j)∈M
[δ−C
Θ
(i, j)] +
∑
i∈D
[C
Θ
(i,λ) + δ/2]
+
∑
j∈I
[C
∆
(λ, j) + δ/2)
= δ(|M | +
|D|
2
+
|I |
2
)
−
∑
(i, j)∈M
[C
Θ
(i, j)] +
∑
i∈D
[C
Θ
(i,λ)] +
∑
j∈I
[C
∆
(λ, j)]
=
δ
2
(2|M | + |D| + |I |) − Θ(α)
Hence in either case the claim holds.
Definition of Kendall-Tau (with Ties). Let N
1
and
N
2
be two assignments of ranks to the same set of
objects, U (with the possibility of ties). Where P is
the set of all two-element sets of distinct objects from
U, define a penalty function p on any {T
i
,T
j
} ∈ P ,
such that (i) p({T
i
,T
j
}) = 1 if the order in N
1
is the
reverse of the order in N
2
, (ii) p({T
i
,T
j
}) = 0.5 if
there is a tie in N
1
but not in N
2
or vice-versa and
(iii) p({ T
i
,T
j
}) = 0 otherwise. The Kendall-Tau dis-
tance (with ties) between N
1
and N
2
, τ(N
1
,N
2
), is
∑
{T
i
,T
j
}∈P
[p({T
i
,T
j
})] ×
2
m×(m−1)
Details of the Data Set for Kendall-Tau Experi-
ments. Section 4 reports experiments quantifying the
difference between neighbour files computed by dis-
tance and similarity, when the two are related by the
conversion in Lemma 1. The experiments used a set
of 1334 trees, taking each tree in turn and ranking all
the remaining trees. The trees represent syntax struc-
tures and originate in a data-set which was used in a
shared-task on identifying inter-node semantic depen-
dencies (Haji et al., 2009). See (Emms and Franco-
Penya, 2011) for download information concerning
this data.
Further A-dualizing Conversions. Concerning A-
duals, there are besides the conversions given in
Lemma 1, others which also generate A-duals.
Lemma 7. For any C
∆
, for any k, let C
Θ
be defined
according to (iii) below.
(iii)
C
Θ
(x,λ) = kC
∆
(x,λ)
C
Θ
(λ,y) = kC
∆
(λ,y)
C
Θ
(x,y) = (1− k)(C
∆
(x,λ) +C
∆
(λ,y)) −C
∆
(x,y)
Then for any α : S 7→ T
∆(α) + Θ(α) = (1− k) × (
∑
s∈S
(C
∆
(s,λ)) +
∑
t∈T
(C
∆
(λ,t)))
Lemma 8. For any C
Θ
, for any k, let C
∆
be defined
according to (iv) below.
(iv)
C
∆
(x,λ) = C
Θ
(x,λ) + kC
Θ
(x,x)
C
∆
(λ,y) = C
Θ
(λ,y) + kC
Θ
(y,y)
C
∆
(x,y) = k(C
Θ
(x,x) +C
Θ
(y,y)) −C
Θ
(x,y)
Then for any α : S 7→ T,
∆(α) + Θ(α) = k× (
∑
s∈S
(C
Θ
(s,s)) +
∑
t∈T
(C
Θ
(t,t)))
The proofs of these follow a similar pattern to that of
Lemma 1 and are omitted. In a similar fashion both
these conversions will give A-duals.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
24
