A DETERMINISTIC MODEL OF BONE MARROW WITH

HOMEOSTATIC PROPERTIES AND WITH STEADY

PRODUCTION OF DIFFERENTIATED CELLS

Manish P. Kurhekar and Umesh A. Deshpande

Department of Computer Science and Engineering, Visvesvaraya National Institute of Technology, Nagpur, India

Keywords: Stem cell modeling, Agent based simulation.

Abstract: There is a significant interest in studying stem cells, to learn about the biological functions during

development and adulthood as well as to learn how to utilize them as new sources of specialized cells for

tissue repair. Modeling of stem cells not only describes, but also predicts, how a stem cell’s environment

can control its fate. The first stem cell populations discovered were Hematopoietic Stem Cells (HSCs). In

this paper, we present a biologically feasible deterministic model of bone marrow that hosts HSCs. Our

model demonstrates that a single HSC can populate the entire bone marrow. It almost always produces

sufficient number of differentiated cells (RBCs, WBCs, etc.). It also overcomes the biological feasibility

limitations of previously reported models.

We have performed agent-based simulation of the model of bone marrow system proposed in this paper. We

have included the details and the results of this validation using simulation in the Appendix. The simulation

also demonstrates that a large fraction of stem cells do remain in the quiescent state. The program of the

agent-based simulation of the proposed model is made available on a public website.

1 INTRODUCTION

Stem cells and their descendents are the building

blocks of life. How stem cell populations guarantee

their maintenance and self-renewal, and how

individual stem cells decide to transit from one cell

stage to another to generate different types of mature

differentiated cells are long standing and fascinating

questions (Roeder and Radtke, 2009). There is a

significant interest in studying stem cells, both to

elucidate their basic biological functions as well as

to learn how to utilize them as new sources of

specialized cells for tissue repair (O'Neill and

Schaffer, 2004). There are several major challenges

within the field, such as the identification of new

signals and conditions that regulate and influence

cell function, and application of this information

towards the design of stem-cell bioprocesses and

therapies. Both of these efforts can significantly

benefit from the synthesis of biological data into

quantitative and increasingly mechanistic models

that describe and predict how stem cell can control

its fate.

Blood is the life preserving fluid, whose major

functions are supply of nutrients and oxygen to the

tissues, self-immunity and defense against

pathogens. In order to carry out these tasks, human

blood contains a variety of cells, each precisely

adapted to its specific objective. All the different

blood cells develop from a kind of a master cell,

called the Hematopoietic (blood forming) Stem Cell

(HSC). HSCs are stem cells that give rise to all the

differentiated blood cell types including White

Blood Cells (WBC), Red Blood Cells (RBC) and

Platelets. HSCs are primarily present in the bone

marrow. Fully mature differentiated cells migrate

into the blood stream leaving back an empty space in

the bone marrow. The transition of HSCs from

quiescence (not undergoing any cell cycle) into

proliferation, or differentiation, is governed by their

cell-cycling status and by hormones secreted by

neighboring cells in their immediate

microenvironment.

It is believed that one HSC is sufficient to

reconstitute the entire blood system (De Haan,

Dontje and Nijhof, 1996). This extraordinary

regenerative ability of the bone marrow is not

surprising, considering that it has a vital role that

P. Kurhekar M. and A. Deshpande U..

A DETERMINISTIC MODEL OF BONE MARROW WITH HOMEOSTATIC PROPERTIES AND WITH STEADY PRODUCTION OF DIFFERENTIATED

CELLS.

DOI: 10.5220/0003706200150023

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 15-23

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

must remain unaffected by stem cells depletion, e.g.

as a result of chemotherapy, radiation or disease. It

should be emphasized that though the supply of

blood cells in the periphery is steady, the bone

marrow, considered as a physical entity is not static.

It is dynamic in the sense that it constantly changes

in its constitution and arrangement, and these

changes occur at varying rates. The bone marrow is

in the state of homeostasis that can be considered as

a dynamic equilibrium between its constituents.

Theise and Harris (2006) in their paper describe

how stem cells and their lineages are examples of

complex adaptive systems. Profound understanding

of a complex adaptive system can be gathered by

generating computer models using computational

techniques. Agent based modeling is a way to

represent such complex adaptive systems in

software. An agent is a high-level software

abstraction that provides a convenient and powerful

way to describe a complex software entity in terms

of its behavior within a contextual computational

environment. Agents are flexible problem-solving

computational entities that are reactive (respond to

the environment), autonomous (not externally

controlled) and interact with other such entities.

To understand the behavior of the blood system,

modeling of HSCs and their behavior in different

circumstances is an area of active research. One of

the significant contributions to stem cell modeling

was a paper by Agur, Daniel and Ginosar (2002).

The main aim of their paper was to provide a

mathematical basis for the bone marrow

homeostasis. More precisely, they wanted to define

simple properties that enabled the bone marrow to

rapidly return to a steady supply of blood cells after

relatively large perturbations in stem-cell numbers.

Their model is represented as a family of cellular

automata on a connected, locally finite undirected

graph. Their model can be briefly described as

follows. It has three types of cells, stem cells,

differentiated cells and null cells. Each cell has an

internal counter. Stem cells differentiate when their

immediate neighborhood is saturated with stem cells

and their internal counter reaches a certain threshold.

A differentiated cell converts to a null cell after its

internal counter crosses the required threshold – a

process that denotes the passing of a differentiated

cell to blood stream leaving empty the place it had

earlier occupied in the bone marrow. A null cell,

with a stem cell neighbor, is converted to a stem cell

when its internal counter reaches a particular

threshold.

d’Inverno and Saunders (2005) have listed the

following drawbacks of Agur et al.’s (2002) model.

1. The specification of Agur et al’s model reveals

that the null cells must have counters. In a sense, an

empty space has to do some computational work.

This lacks biological feasibility and is against what

the authors state about modeling cells, rather than

empty locations, having counters.

2. Stem cell division is not explicitly represented;

instead, stem cells are brought into existence in

empty spaces.

3. A stem cell appears when a null cell has been

surrounded by at least one stem cell for a particular

period. However, the location of the neighboring

stem cell can vary at each step.

4. In the model, if a stem cell is next to an empty

space long enough then it divides so that its

descendent occupies this space. However, an empty

cell might be a neighbor of more than one stem cell.

The rule does not state that a particular neighboring

stem cell must be present for every tick of the

counter. Biologically it would be more intuitive to

have the same stem cell next to a null cell for the

threshold length of time in order for division to

occur into the null cell space but the model lacks any

directional component.

5. The state of a stem cell after division is not

defined. Nothing is said about what happens to a

stem cell after a new stem cell appears in the null

cell space. For example, should the counter of the

stem cell be reset after division? Neither does it give

any preconditions on the particular neighboring stem

cell S that was responsible for converting the null

cell space to a stem cell. For example, should S’s

local counter have reached an appropriate point in its

cycling phase for this to happen?

In order to overcome the limitations, d’Inverno and

Saunders (2005) introduced the concept of a

controlling microenvironment that links a null cell

that has reached a threshold with a stem cell that can

differentiate. All the cells send and receive signals

from the microenvironment and act on its

suggestions. They also performed an agent based

implementation with the incorporation of Agur et

al.’s model in two dimensions. However, the

improvement suggested by them does not have any

biological basis. Moreover, there are additional

limitations of the model described by Agur et al.,

which have not been considered by d’Inverno and

Saunders (2005). The additional limitations are

discussed below.

1. There are no intermediate cells or transitive cells

in the model proposed in Agur et al. (2002).

Transitive cells are intermediate cells that have

limited stem cell like properties and they are

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

eventually converted to mature differentiated cells.

For Hematopoietic system, common lymphoid

progenitor (CLP) and common myeloid progenitor

(CMP) are transitive cells (Gordon, 2007).

2. As an effect of the fourth drawback mentioned

above, a stem cell can potentially differentiate more

than once in the same time instant since it might be

surrounded by more than one empty cell. Hence, it

can potentially convert more than one of its

neighboring empty cells into stem cells. Clearly, this

lacks biological feasibility.

In this paper, we have addressed all the limitations

by augmenting the model proposed by Agur et al.

(2002), thereby making the model closer to

biological reality. The model we present is aimed to

simulate a situation in which a cell’s behavior is

determined only by a combination of the types and

states of cells in its proximity and its own cell cycle

represented by its internal counter. The main

assumptions of our model are:

• Cell behavior is determined by the number and

type of its neighbors. This assumption is aimed at

describing the fact that cytokines, secreted by cells

into the microenvironment are capable of activating

cells into changing their types (De Haan et al., 1996)

(Roeder and Radtke, 2009).

• Each cell has internal counters, which determine

the time required by the cells to change its type, as

well as the transit time of a differentiated cell before

it migrates to the blood stream.

To validate the model, we have performed an agent-

based simulation of the model of bone marrow stem

cell system proposed in this paper. The program for

the same is available on the website:

http://sites.google.com/site/stemcell

model. We have included the results of validation of

the proposed model using agent-based simulation in

the Appendix.

The paper is organized as follows. In the next

section, we describe our model and the rules that

govern it. Later we show how a single stem cell can

populate the bone marrow. In section 3, we show

that the model almost always provides a steady

supply of differentiated cells to the blood stream. In

section 4, we show the steady states and death and

we conclude the paper in section 5. The results of

the agent-based simulations are included in the

Appendix.

2 DESCRIPTION OF THE

MODEL

Our model contains three basic types of cells and a

notation for an empty space:

• Stem cell (S), either can proliferate generating

new stem cells or can convert to a transitive cell.

• Transitive cell (T), either can convert to a

differentiated cell or can convert back to a stem cell

when there are no stem cells in its near

neighborhood.

• Differentiated cell (D), is the final product of a

stem cell. After maturation, these cells leave the

bone marrow and circulate in the blood, leaving

back empty space.

• Empty space (E), represents vacant space in the

bone marrow.

In our model, the bone marrow is represented as a

connected, locally finite undirected graph. This

describes the neighborhoods of bone marrow cells.

Let G = (V, L) be a connected, locally finite

undirected graph that denotes the bone marrow. Its

vertex set V denotes the cells and the set of edges L

describes the neighboring cells to which a cell is

connected to in the bone marrow (Figure 1).

Figure 1: Example graph showing part of bone marrow

system in 2-Dimension. Each vertex is a cell and it has

eight neighbors. The label of vertex denotes its type.

Diagrammatically, the transitions of different

types of cells in Agur et al.’s (2002) model and our

proposed model are depicted in Figure 2 (N denotes

a null cell in Agur et al.’s model).

For every u, v ∈ V we denote by ρ(u, v) the

distance between these vertices in the shortest-path

metric induced by G. N(v) = {u ∈ V |ρ(u, v) = 1}

denotes the immediate neighborhood of a vertex v ∈

V, i.e. the set of vertices joined to v by an edge. B(v,

n) denotes the ball of radius n centered in v ∈ V. It is

A DETERMINISTIC MODEL OF BONE MARROW WITH HOMEOSTATIC PROPERTIES AND WITH STEADY

PRODUCTION OF DIFFERENTIATED CELLS

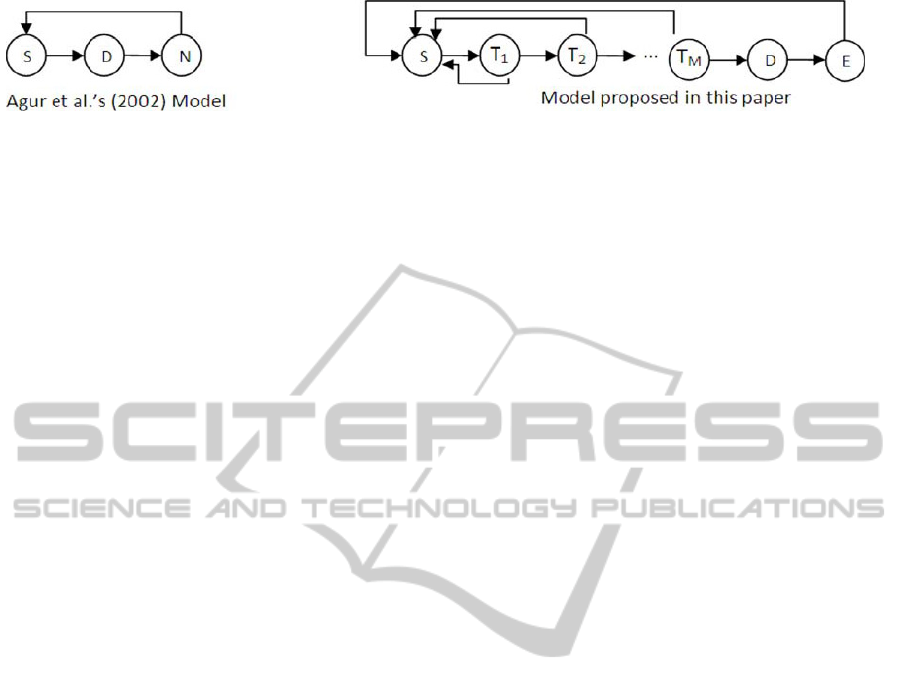
Figure 2: Comparison of Agur et al.'s (2002) model and the model proposed in this paper.

the set of all vertices such that their distances from v

do not exceed n. We write B(v, n) = {u ∈ V |ρ(u, v) ≤

n}. B(v, n) defines the near neighborhood of size n

of vertex v.

If U ⊆ V is a nonempty subset of vertices then

for every v ∈ V let ρ

(v) = min

∈

ρ(u, v) be the

minimum distance between v and another vertex u

contained in set U.

A state of a vertex is a 1-tuple, a 2-tuple or a 3-

tuple depending on the cell type. The first coordinate

denotes the cell’s type (S, T, D or E denoting a stem

cell, a transitive cell, a differentiated cell or an

empty space respectively). For a stem cell, the

second coordinate denotes the direction of

proliferation and the third coordinate denotes the

simulated time τ as an internal counter. For a

transition cell, the second coordinate denotes its

generation (progeny) while the third coordinate

denotes the simulated time. A differentiated cell has

only two coordinates and the second coordinate

denotes the simulated time. Finally, an empty space

does not have any counter or any other property,

thus it has a single coordinate that denotes the type.

Let µ be the maximum number of immediate

neighbors possible for any cell. µ also denotes the

number of directions for a stem cell to proliferate. A

stem cell, when it proliferates, can occupy an empty

space, if available, in its immediate neighborhood.

A transitive cell can go through several

generations (progeny) before it converts to a

differentiated cell. A transitive cell moves from one

generation to another after its internal counter

reaches a certain threshold. There are M generations

for a transitive cell, where M is greater than or equal

to 1. When a transitive cell has moved into its last

generation (i.e. M

generation) and when its internal

counter reaches a threshold, it converts to a

differentiated cell. In circumstances when there is

not even a single stem cell in the near neighborhood

of a transitive cell, a transitive cell converts back to

a stem cell. The rules given below also capture the

fact that a transitive cell’s ability to convert back to

a stem cell diminishes with each subsequent

generation. Let η denote the distance multiple for a

transitive cell to convert back to a stem cell. Thus,

the conversion from a transitive cell to a stem cell

depends on the distance multiple η and its current

generation.

Let Ω be the set of states of a vertex.

A map x: V → Ω is the state of the entire graph. The

set of all the states of the bone marrow graph G is

denoted by Ω

. A state x ∈ Ω

of the bone marrow

graph G at time t is denoted by x

. The state of a

vertex v at time t is denoted by x

(v).

With the above definitions, we are now ready to

define the rules of an iterative operator on all states

Ω

. It depends on three positive nonzero integers Φ,

Ψ, and Θ. The rules for the state changes can be

regarded as describing a family of cellular automata.

The first sub-rule of rule (1) states that a stem

cell converts to a transitive cell, if its internal

counter representing its cycling phase has reached a

threshold Ψ and its immediate neighborhood consists

only of stem cells. This corresponds to receiving a

signal that the microenvironment is saturated with

stem cells. The evidence for such a feedback is

provided by De Haan et al. (1996), where the

authors show that Hemopoietic cell amplification in

vivo is regulated by various mechanisms that appear

to be under control of many Hemopoietic growth

factors, including the activation and deactivation of

the quiescent stem cells into the cell cycle. The

second sub-rule within this rule specifies that if a

stem cell’s internal counter has reached a threshold

Ψ but its immediate neighborhood is not saturated by

stem cells, then the stem cell enters into a quiescent

state, i.e. it retains the same state. The third sub-rule

states that when a stem cell’s internal counter

reaches a threshold Ψ and there exists an empty

space in its neighborhood, then it proliferates such

that one of its descendants occupies the empty space

and the other remains in the original location. The

sub-rule also defines that the new stem cell as well

as the stem cell at original location receive the

renewed biological time. With this sub-rule, we also

denote a systematic way of choosing the empty

space for proliferation. The method we propose is by

adding a directional component d in the state of

every stem cell and by arranging all the possible

directions µ in a circular (round-robin) order. A stem

cell proliferates in the empty space in the direction

of the directional component d of its state. If the

direction given by the directional component d of

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

(1)

(2)

(3)

(4)

the state is occupied by any cell, then the stem cell

continues to choose the next direction, in the round-

robin order, for availability of the empty space.

After proliferation, the directional component of

stem cell is incremented to point to the next

direction. The last sub-rule states that if the internal

counter of a stem cell has not reached a threshold Ψ

then it is just incremented.

Transitive cells are intermediate cells that can

convert back to stem cells if there are not enough

stem cells in their near neighborhood, a situation that

can occur following radiation or organ damage.

Theise and Harris (2006) detail the dedifferentiation,

i.e., reversion of an intermediate cell into a stem cell.

Rule (2) states that when a transitive cell’s internal

counter reaches a threshold Θ it moves on to the

next generation unless it is not in its last (M

)

generation. If a transition cell’s counter has reached

the threshold Θ and it is in its last generation then it

gets converted to a differentiated cell. In certain

circumstances when a transitive cell does not have

any stem cell in its near neighborhood then it gets

converted back to a stem cell. The near

neighborhood is governed by a constant η and the

generation of the transitive cell. The stem cell like

property of a transitive cell goes on decreasing with

subsequent generations. The near neighborhood size

to find a stem cell keeps on increasing with each

subsequent generation of a transitive cell, implying

its reduced capacity to regenerate and the

requirement of an even stronger signal to convert

back to a stem cell.

Rule (3) states that when a differentiated cell’s

internal counter reaches a threshold time Φ, it

maturates. After maturation, the cell migrates to the

blood stream leaving the original space occupied by

the differentiated cell as empty space.

Rule (4) specifies that an empty space does not

change by itself. It does not have any internal

counter nor is involved in any computation.

We show next that the proposed model has

strong homeostatic properties, similar to Agur et

al.’s model.

3 HOMEOSTASIS PROPERTY OF

THE BONE MARROW MODEL

We begin by investigating the property of stem cells

to expand throughout the bone marrow. The

following lemma shows that any point in the bone

marrow graph gets occupied by a stem cell, given

that initially there is at least one stem cell in the

bone marrow graph.

Lemma 1. For any Φ, Ψ, Θ if there exist two vertices

u, v ∈ V such that at some time t, vertex v is not

occupied by a stem cell and u is, then there exists an

s > 0 such that v will be occupied by a stem cell at

time t + s.

Proof: From rule (1), we conclude that if u and v are

neighbors then u remains a stem cell as long as v is

not a stem cell. The vertex v itself turns into a stem

cell in no more than Φ+μΨ time steps. This is the

maximum time required including the time required

for cell at vertex v to migrate to the blood stream (in

case it was a differentiated cell), turn into an empty

space and as it is a neighbor of a stem cell, become a

stem cell after a maximum μΨ time steps. We can

use induction on the distance ρ(u, v) to obtain a

bound on the time that is needed for v to turn into a

stem cell:

s ≤ Φ + μ ρ(u, v)

Ψ (5)

The proof above conveys that the distance ρ

U(t)

(v)

between a vertex v, which is not occupied by a stem

cell at time t, to the subset U(t) ⊆ V of vertices

which includes a stem cell vertex at time t is a non-

increasing function. Furthermore, there exists s ≤ Φ

+ μρ

U(t)

(v)Ψ such that ρ

U(t+s)

(v) = 0.

We now show that if r ≥ t + s then ρ

U(r)

(v) ≤ Mη

in any two consecutive time slots. This means that

from the time t + s onwards there always is a stem

A DETERMINISTIC MODEL OF BONE MARROW WITH HOMEOSTATIC PROPERTIES AND WITH STEADY

PRODUCTION OF DIFFERENTIATED CELLS

cell not farther than Mη edges from v in any two

consecutive time slots.

Lemma 2. Suppose that a vertex v becomes a stem

cell at time t

, then for every t ≥ t

there is a vertex u

∈ B(v, Mη) which is occupied by a stem cell at time t

or t+1.

Proof: A necessary condition for the production of a

stem cell at a vertex v at time t

is that ∃v’ ∈ N(v),

−1

(v’) = (S,*, Ψ). Now, the cell at vertex v remains

a stem cell until last three conditions of rule (1) hold.

Therefore, if the cell at vertex v becomes a transitive

cell at time t

> t

, either it still has a stem cell

neighbor at time t

or all of its neighbors become

transitive cells simultaneously with v. If it is the first

scenario then we are done. The second scenario can

happen only if all the stem cells have their internal

counters synchronized and reach the threshold Ψ

simultaneously at time t

. In such a case, either there

is a stem cell in the near neighborhood of size Mη or

the vertex v will again convert from a transitive cell

to a stem cell at time t

+ 1 as all its near neighbors

are not stem cells. Thus if v is not a stem cell, there

is a stem cell in B(v, Mη) at time t

or t

+1. Applying

Lemma (1) ensures that until the next time the vertex

v is occupied by a stem cell, the distance from v to

the closest stem cell will not exceed Mη in any two

given consecutive time instances.

A direct conclusion from Lemma (2) is the

estimation for the density of stem cells in bounded

vicinity. We state the same in the following lemma

for graphs with bounded degree. The bone marrow

can be described as a graph of bounded degree with

each vertex connected only to its adjacent vertices.

We need two more notations:

If the graph G has the property that there exists Δ

such that |N(v)| ≤ Δ, ∀v ∈ V, we say that G has

bounded degree, and write deg(G) ≤ Δ.

The density of stem cells in a given finite subset of

vertices U ⊂ V at time t is the proportion at time t of

the number of stem cells S in U and the total number

of vertices in U. It is denoted by δ

t (U).

Lemma 3. Let G be a graph of bounded degree.

Suppose that at some time t

a vertex v is occupied

by a stem cell, then for every ball B = B(v, Mη) ⊂ G,

limt→∞ δt (B) ≥ 1/(2*(Δ

Mη

+ 1)).

Proof: By Lemma (1) and Lemma (2), any ball of

radius Mη admits a stem cell from a certain moment

on for any two consecutive time slots. The size of

such a ball contains less than or equal to Δ

Mη

+ 1

vertices.

In essence Lemma (1), Lemma (2) and Lemma (3)

show that not only is it true that one stem cell is

sufficient to bring back the bone marrow system

homeostasis, it is also true that the bone marrow has

a built-in mechanism guaranteeing that stem cells do

not become too scattered. Every ball of radius Mη is

occupied by at least one stem cell at any two

consecutive time steps from the moment it was

occupied by a first stem cell.

4 STEADY PRODUCTION OF

DIFFERENTIATED CELLS

We have seen that stem cells do fill the bone marrow

graph nicely. In this subsection, we show that the

system almost always generates enough mature

differentiated blood cells. Before proving the same,

we mention some observations:

• When a transitive cell is created and if it has a

stem cell neighbor, then it would always proceed to

create a differentiated cell. The stem cell neighbor

will remain a stem cell at least till the time a

transitive cell becomes a differentiated cell, the

differentiated cell becomes an empty space and the

empty space is occupied by another stem cell.

• Starting from non-saturated, if the complete

available space is to be saturated with stem cells

then every stem cell should divide into two stem

cells and any stem cell should not convert to a

transitive cell. If any stem cell converts to a

transitive cell, then the condition above will ensure

that it becomes a differentiated cell.

An extreme situation can occur, when the system

contains only stem cells at a time t and the internal

counters of all stem cells are synchronized. In such a

case, all the stem cells will convert to transitive cells

on or before t + Ψ. At the next time instant, all these

transitive cells will convert back to stem cells, as

there will not be a single stem cell in their near

neighborhood. This system would not produce any

differentiated cells, but will also not die out. We can

call such a state as resonant state as the cells will

resonate between stems cells and transitive cells

without producing any differentiated cells.

A resonant state can occur for a block of holding

capacity of 2

cells if it is occupied completely by

stem cells starting from a single stem cell in μΨ

number of time steps. The physical occupancy of

stem cells in a given block depends largely on the

round-robin way of choosing the directions and

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

initial stem cell population. If the manner in which

the round-robin arrangement of directions is

clockwise or counter-clockwise then the resonant

state would not occur, if starting with a single cell in

two dimensional space as 2

/μ

is greater than 1

when μ is greater than 4. For example, with μ = 8 in

a two dimensional space, 2

= 512 thus in 8Ψ time

steps 512 cells would be generated, but the ball of

radius 8 from the vertex v can hold only (8+1+8)

289 number of cells. Thus, some stem cell would be

surrounded by stem cells within 8Ψ time steps and it

would convert to a transitive cell. The possibility of

reaching a resonant state drops further after

considering the co-ordination of a similar event in

neighboring blocks.

A resonant state would occur if all the cell

positions are occupied by stem cells and their

internal time is also synchronized. This is an

extreme case. Thus, there are very few resonant

states out of the total number of states and hence,

there is a very low possibility that the model will be

in a resonant state.

Lemma 4. Suppose that a vertex v ∈ V is occupied by

a stem cell or a transitive cell at time t. Then either v

or one of its near neighbors in B(v, Mη) will be

occupied by a differentiated cell within (μ+1)Ψ +

(M+1)Θ + 1 iterations unless the system is in a

resonant state.

Proof: Assume that at vertex v there is a stem cell

that has no differentiated neighbors, otherwise we

are done. N(v) will consist only of stem cells by at

most μΨ time steps. Then v or one of its neighbors

will convert to a transitive cell after Ψ time steps.

Such a transitive cell will always have stem cells in

near neighborhood. Then after M generations of a

transitive cell, it would convert to a differentiated

cell, i.e. after (M+1)Θ time steps.

If v is a transitive cell and if v has a stem cell in its

near neighborhood then after (M+1)Θ time steps it

becomes a differentiated cell. If v is a transitive cell

and if v does not have any stem cell in its near

neighborhood, it becomes a stem cell in the next

time instance and the argument above follows.

Thus, except in the case of a resonant state, there

is a differentiated cell every (μ+1)Ψ + (M+1)Θ + 1

iterations in B(v, Mη).

Lemma (4) shows that in an eventuality of a

severe perturbation, a transitive cell will convert

back to a stem cell and bring back the entire system

to a steady state as shown in Lemma (3).

Note that in this model, one cannot guarantee

that a particular stem cell will eventually be

converted to a differentiated cell. The lemma above

does guarantee that in the close vicinity of any stem

cell some cell differentiates during a fixed bounded

time interval unless the system is not in a resonant

state. An immediate consequence of this is a lower

bound on the supply of differentiated cells to the

blood stream.

Corollary 5. Suppose that at some time t

a vertex v

is occupied by a stem cell, then every ball of radius

2Mη eventually supplies at least one mature cell

every (μ+1)Ψ + (M+1)Θ +1 + Φ time steps unless

the system is in a resonant state.

Proof: By Lemma (3), every ball of radius Mη

admits a stem cell from a certain moment onwards in

any two consecutive time instances. Lemma (4) says

that either this cell or one of its near neighbors (and

so we argue about balls of radius 2Mη) converts to a

differentiated cell within (μ+1)Ψ + (M+1)Θ +1 time

steps and migrate from the bone marrow as mature

cells after Φ additional time steps. Thus, every ball

of radius 2Mη eventually supplies at least one

mature cell every (μ+1)Ψ + (M+1)Θ + 1 + Φ time

steps.

5 STEADY STATES AND DYING

OUT STATES OF THE BONE

MARROW MODEL

We consider the unique state satisfying ∀v ∈ V, x(v)

= (E) ∨ x(v) = (D,*) as the death state of the system.

A state x

for which there exists a k ∈ Z

such that x

t+k

is the death state, will be called a dying out state.

Thus, a state not consisting of a single stem cell or a

transitive cell is a dying out state. We claim that

there is no other dying out state.

Lemma 6. The dying out states are only those

consisting of no stem cells or no transitive cells.

Proof: Let x

∈ Ω be a state, which is not one of the

dying out states. If there exists v ∈ V which is not a

stem cell at time t and since there exists a stem cell

at time t, v turns to a stem cell by Lemma (1). So by

Lemma (2) there is always a stem cell in B(v, Mη) in

any two consecutive time instants from the time v

has converted to a stem cell. The system does not die

out. Even if v is a transitive cell then it will become

a stem cell if there is no stem cell in its near

neighborhood.

Assume, therefore, that V admits only stem cells at

time t. If the counters are not synchronized they do

A DETERMINISTIC MODEL OF BONE MARROW WITH HOMEOSTATIC PROPERTIES AND WITH STEADY

PRODUCTION OF DIFFERENTIATED CELLS

not convert to transitive cells at the same time

instance and the system does not die out. If the

counters are synchronized they enter into resonant

state and again the system does not die out.

Thus, we have proved that the model

representing the bone marrow is dynamic in the

sense that it continuously changes in its constitution

and arrangement, and these changes occur at varying

rates depending on the constants Φ, Ψ, and Θ. We

have also seen that except for the death state, the

system never dies out. The bone marrow is in the

state of a dynamic equilibrium that can be

considered as if it is in homeostasis.

If there exist states x ∈ Ω in which for all k ∈ Z

t+k

= x

, then these are the steady states of the

system.

Lemma 7. For every Φ, Ψ, Θ the model does not

have steady states other than the death state and the

resonant state.

Proof: The fact that each differentiated cell matures

and leaves the bone marrow eventually, combined

with Lemma (1) and Lemma (6) implies the above.

6 DISCUSSION

In this paper, we have proposed a biologically

feasible model of bone marrow by extending the

model of Agur et al. (2002). The proposed model

adds the ability to recover from severe perturbations

of the bone marrow by adding rules that can convert

a transitive cell back to a stem cell and bring back

the system homeostasis.

The main properties of our model are achieved

from the feedback demand of rule (1), namely that a

stem cell does not convert to a transitive cell unless

its immediate microenvironment is saturated with

stem cells. The feedback demand in rule (2) is also

significant in the sense that a transitive cell can

convert back to a stem cell in cases of severe

perturbations resulting into loss of several stem

cells. We obtain the results that stem cells are

eventually dense (Lemma 2 and Lemma 3) and that,

let alone the case when there is no stem cell or

transitive cell, the system never dies out (Lemma 6).

Even though our extension of the Agur et al.’s

model is simple, the properties that emerge are

general, and hold for more complex descriptions. It

is a step ahead in the direction to model the

immensely complex bone marrow system.

Our extension of Agur et al.’s model removes all

the drawbacks associated with it. To summarize:

1. Our model has empty spaces but they no longer

need any counters.

2. In the model, a stem cell division is explicitly

represented.

3. The model has incorporated a directional

component for the division of stem cells.

4. A stem cell’s internal counter comes back to its

initial state after division; i.e. it becomes a true

daughter stem cell. Thus, a stem cell divides into

two identical daughter stem cells.

5. Transitive cells that have limited ability to

convert back to stem cells are represented in our

model. Their ability to regenerate to a stem cell

diminishes with subsequent generations.

6. One stem cell divides into a single empty space.

For another division, the stem cell has to wait for its

internal counter to reach a threshold as its internal

counter gets reset after division.

Our model overcomes all the drawbacks of Agur et

al.’s (2002) model. It also does not require message

passing between cells and the controlling

microenvironment, as required by the model of

d’Inverno and Saunders (2005). Hence, it is closer to

biological reality. The validation of this fact is

underscored by the agent-based simulations that we

have carried out. The results of these simulations are

included in the Appendix. These simulations also

demonstrate that, as predicted, large fractions of

stem cells do remain in the quiescent state (Gordon,

2007).

There are several other options of bringing the

model even more closer to biologically observed

complexity. There are two extensions that we would

like to work on in the future. The first is to make a

provision of apoptosis (cell death) for all types of

cells. Secondly, we can provide a stochastic

behavior for the stem cell proliferation to capture

variations in the human hematopoietic system.

Addition of the stochastic behavior will also enable

the introduction of a randomized directional

component. We would also like to increase the scale

of the simulation of the bone marrow system and to

perform the same in three-dimensional space,

typically with simulated bone marrow size that can

hold 10

to 10

number of cells and with the model

constants matching observed parameters (Michor,

Hughes, Iwasa, Branford, Shah, Sawyers and

Nowak, 2005).

REFERENCES

Agur Z., Daniel Y. and Ginosar Y. (2002). The Universal

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

Properties of Stem Cells as pinpointed by a Simple

Discrete Model. In Journal of Mathematical Biology,

44(1):79-86.

De Haan G., Dontje B. and Nijhof W. (1996). Concepts of

Hemopoietic Cell Amplification. Synergy,

Redundancy, and Pleiotropy of Cytokines affecting the

Regulation of Erythropoiesis. In Leukemia Lymphoma,

22(5-6):385-94.

Gordon M. (2007). Stem Cells and Haemopoiesis. In

Hoffbrand A., Catovsky D. and Tuddenhan E. (Eds.),

Postgraduate Haematology, pp. 1-12. Blackwell

Oxford, 5

edition.

d’Inverno M. and Saunders R. (2005). Agent-based

Modeling of Stem Cell self-organization in a Niche,

Engineering Self- Organizing Systems: Methodologies

and Applications. In Brueckner S., Di Marzo G.,

Serugendo, Karageorgos A. and Nagpal R. (Eds.),

LNAI, 3464. Springer.

Michor F., Hughes T., Iwasa Y., Branford S., Shah N.,

Sawyers C. and Nowak M. (2005). Dynamics of

chronic myeloid leukaemia. In Nature

435(7046):1267-70.

O'Neill A. and Schaffer D. (2004). The biology and

engineering of stem-cell control. In Biotechnology and

Applied Biochemistry 40(Pt 1):5-16.

Roeder I. and Radtke F. (2009). Stem Cell Biology meets

Systems Biology. In Development 136(21):3525-30.

Theise N. and Harris R. (2006). Postmodern Biology:

(Adult) (Stem) Cells Are Plastic, Stochastic, Complex,

and Uncertain. In Handbook of Experimental

Pharmacology (174): 389-408.

APPENDIX

An agent-based model was developed for the bone

marrow system proposed in this paper. We have

implemented the program in the C programming

language and it is available at the following website:

http://sites.google.com/site/stemcellmodel.

The results given below are on a two

dimensional grid of size 30 x 30 for the following

constants:

Φ = 4 Constant for differentiated cells.

Ψ = 1 Constant for stem cells.

Θ = 1 Constant for transitive cells.

η = 2 Constant for distance measure for near

neighborhood from a particular transitive cell.

μ = 8 Number of directions in a 2-D space.

M = 3 Number of generations of transition cells.

We specified colors like Silver (S), Titanium Yellow

(T), and Dark Red (D) to stem cells, transitive cells,

and differentiated cells respectively. Also note that

the directional component moves in the clockwise

manner.

Simulation 1:

Starting with 10% stem cells

Figure 3: Initial Screen (with 10% stem cells).

Figure 4: After 100 time steps, 93.3% stem cells quiescent.

Figure 5: After 3000 time steps, 88% stem cells quiescent.

Simulation 2: Starting with single stem cell at top

left.

Figure 6: After 100 time steps, 91.9% stem cells quiescent.

A DETERMINISTIC MODEL OF BONE MARROW WITH HOMEOSTATIC PROPERTIES AND WITH STEADY

PRODUCTION OF DIFFERENTIATED CELLS