IMPORTANCE OF INPUT PARAMETER SELECTION FOR

SYNTHETIC STREAMFLOW GENERATION OF DIFFERENT

TIME STEP USING ANN TECHNIQUES

Maya Rajnarayn Ray

and Arup Kumar Sarma

Research Scholar, Department of Civil Engineering, Indian Institute of Technology, Guwahati, India

Department of Civil Engineering, Indian Institute of Technology, Guwahati, India

Keywords: Synthetic streamflow, Artificial neural network, Input parameters, Time step discretization.

Abstract: Streamflow time series is gaining importance in planning, management and operation of water resources

system day by day. In order to plan a system in an optimal way, especially when sufficient historical data

are not available, the only choice left is to generate synthetic streamflow. Artificial Neural Network (ANN)

has been successfully used in the past for streamflow forecasting and monthly synthetic streamflow

generation. The capability of ANN to generate synthetic series of river discharge averaged over different

time steps with limited data has been investigated in the present study. While an ANN model with certain

input parameters can generate a monthly averaged streamflow series efficiently, it fails to generate a series

of smaller time steps with the same accuracy. The scope of improving efficiency of ANN in generating

synthetic streamflow by using different combinations of input data has been analyzed. The developed

models have been assessed through their application in the river Subansiri in India. Efficiency of the ANN

models has been evaluated by comparing ANN generated series with the historical series and the series

generated by Thomas-Fiering model on the basis of three statistical parameters- periodical mean, periodical

standard deviation and skewness of the series. The results reveal that the periodical mean of the series

generated by both Thomas –Fiering and ANN models is in good agreement with that of the historical series.

However, periodical standard deviation and skewness coefficient of the series generated by Thomas–Fiering

model are inferior to that of the series generated by ANN.

1 INTRODUCTION

Proper planning, efficient management and optimal

operation of the water resources system is an utmost

need of the recent time. Earlier, water resources

planners used to handle planning and management

with the only available historical hydrological

records. Those approaches have a limitation that

they do not have a futuristic aspect in their planning

because of insufficiency of long series of future data.

As a result, synthetically generated time series is

gaining high importance among researchers which

has lead to the development of several models for

the generation of time series. Forecasting of

streamflows is of vital importance for flood caution,

operation of flood-control-purposed reservoir,

determination of river water potential, production of

hydroelectric energy, allocation of domestic and

irrigation water in drought seasons, and navigation

planning in rivers (Bayazıt, 1988). Conventional

time series models such as Thomas-Fiering model

(Thomas and Fiering, 1962), autoregressive moving

average (ARMA) models, auto-regressive integrated

moving average (ARIMA), autoregressive moving

average with exogenous inputs (ARMAX) and (Box

and Jenkins, 1976) have been applied by many

researches in their studies, as they predict reasonably

accurate results. But the traditional methods suffer

from the limitation of being linear and stationary.

Hence, new technologies and algorithms have come

up as powerful tools for modeling several problems

related to water resources engineering. ANN is one

of them. ANN has been used successfully to solve

different kinds of hydrological problems (ASCE,

2000). Particularly, the ANN approaches when

applied to hydrologic time series modeling and

forecasting have shown better performance than the

classical techniques (Govindaraju and Rao, 2000).

211

Rajnarayn Ray M. and Kumar Sarma A..

IMPORTANCE OF INPUT PARAMETER SELECTION FOR SYNTHETIC STREAMFLOW GENERATION OF DIFFERENT TIME STEP USING ANN

TECHNIQUES.

DOI: 10.5220/0003681802110217

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 211-217

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Ahmed and Sarma (2007) presented ANN model

for generating synthetic streamflow series of the

river Pagladia, Assam in India. Comparing different

models they found that the ANN model is the best in

generating synthetic streamflow series for the

Pagldia Project. Wen and Lee (1998) presented a

neural-network based multiobjective optimization of

water quality management for river basin planning

and water quality control for the Tou-Chen River

Basin in Taiwan. Chandramouli and Raman (2001)

developed a dynamic programming based neural

network model for optimal multi reservoir operation

Parambikulam Aliyar Project. Chandramouli and

Deka (2005) introduced a decision support model

(DSM) based on ANN for optimal operation of a

reservoir in south India. Diamantopoulou et al.

(2006) developed three layer cascade correlation

artificial neural network (CCANN) models for the

prediction of monthly values of some water quality

parameters in rivers Axios and Strymon, at a station

near the Greek Bulgarian borders. Yurekli et al.

(2004) used Thomas-Fiering and ARIMA models

for the daily maximum stream flow. Srinivasulu and

Jain (2006) presented a study on different training

methods available for the training of multi-layer

perceptron (MLP) network for modeling rainfall-

runoff process. Treiber and Schultz (1976) generated

sreamflow data on monthly and daily basis using

Thomas-Fiering model and the Karlsruhe model

type A for computing reservoir capacity. Zealand et

al. (1999) investigated the utility of ANN for short

term forecasting of streamflow. Birikundavyi et al.

(2002) investigated the performance of ANN

methods in prediction of daily streamflows. They

showed that ANN method yielded better results than

ARMA models. Kumar et al. (2004) employed

recurrent neural network (RNN) model in

streamflows forecasting. Stedinger and Taylor

(1982) presented that streamflow construction and

simulation is a process of verification that a

stochastic streamflow model reproduces those

statistics which by design it should reproduce.

In the present study an attempt has been made to

evaluate the efficiency of ANN model to generate

synthetic series of streamflow rate averaged over

different time steps with varying input parameters.

The ANN generated outputs are compared with

conventional Thomas-Fiering model and historical

streamflow of the Lower Subansiri Hydroelectric

Project (LSHEP).

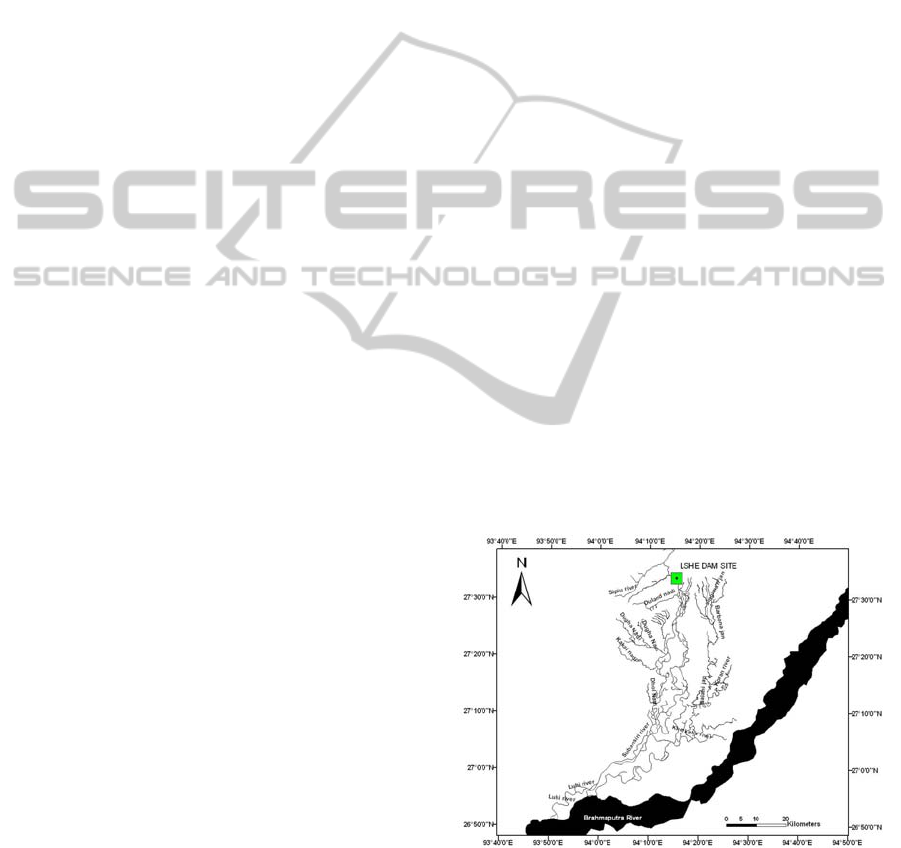
1.1 Study Area

This project is located on the Assam-Arunachal

boarder near North Lakhimpur town of Assam as

shown in Fig.1. The project area lies in the Lower

Subansiri District of Arunachal Pradesh and

Dhemaji District of Assam, India. River Subansiri

originates from the south of the Po Rom peak

(Mount Pororu) at an elevation of 5059 m in the

Tibetan Himalaya. After flowing for 190 km through

Tibet, it enters India. It continues its journey through

the Himalayas of India for 200 km and enters the

plains of Assam through a gorge near Gerukamukh.

The Subansiri is the largest tributary of the

Brahmaputra. Its total length up to the confluence of

Brahmaputra River is 520 km. Its drainage area up

to its confluence of the River Brahmaputra is 37,

000 Sq.km. The river maintains almost a stable

course in the hilly terrain but becomes unstable as

soon as it enters the alluvial plains of Assam.

2 SYNTHETIC STREAM FLOW

GENERATION

The basic assumption in synthetic streamflow

generation is that the streamflow population can be

described by stationary stochastic process. Hence

synthetic streamflow may be generated by fitting

statistical model. In the following sections two

different methods viz. Thomas-Fiering and ANN for

synthetic sreamflow generation are discussed.

Figure 1: Location of the LSHE dam site.

2.1 Thomas-Fiering Model

Thomas Firings method is widely used for the

generation of synthetic streamflow. It is a Markov

Chain model which describes that there is a definite

NCTA 2011 - International Conference on Neural Computation Theory and Applications

212

dependence between the flow of present time step

and that of previous time step. For applying Thomas

Firings method input data is generally transformed

by using different methods like log transformation,

power transformation and Box-Cox transformation

(Box-Cox, 1962) to have the input data in a normal

distribution. In this study log transformation method

is adopted to transfer the historical data. Raman and

Sunil Kumar (1995) and Salas et al. (1985) used the

same method for the transformation of data in their

studies and found it to be quite efficient. Maass et al.

(1970) presented that log transformed data has the

advantage of eliminating the occurrence of negative

flows while generating synthetic streamflow. The

recursive equation of Thomas Fiering model used

for the study is give below:

21/2

1, ,1 ,1 1 , , 1 ,1 ,

(/)( ) (1 )

pt avp pp p p pt avp p pp pt

qq r qq r

σσ

++++ ++

=+ −+−

(1)

where, p = period which may be 10 days or month;

t= year; q

av,p

= mean of the historical streamflow

series for period p(current period t); q

av,p+1

= mean

of the historical streamflow series for period

p+1(next period); σ

and σ

p+1

= standard deviation

of historical series of period p and p+1 respectively;

p,p+1

= correlation between period p and p+1 of

historical series; ξ

p,t

= independent standard normal

random variable; q

p+1,t

= logarithmic predicted value

of period p+1 for particular t. The q

p+1, t

values thus

generated are then transformed to periodical flow by

using the following relationship;

1, 1,

exp( )

pt pt

Using the above model 100 years synthetic

steramflow series is generated for the LSHE project

of different time step.

2.2 Artificial Neural Network (ANN)

Application of ANN is gaining popularity in

different fields. It has been efficiently applied to

solve many problems of water resources and

hydrology. The neural networks are composed of

simple elements operating in parallel. These

elements are analogous to biological nervous

systems. Neurons arranged in a group are called

layers. The neurons in a layer are connected to the

adjacent layer by the means of weights; the network

function is determined largely by the connections

between elements. But in the same layer, these

neurons do not have any connection. A neural

network can be trained to perform a particular

function by adjusting the values of the connections

(weights) between elements. Generally, neural

networks are adjusted, or trained, in order to achieve

a particular target for a give output. Feed forward

neural network is used in the present study. The

network has one input layer with some neurons

where input data is fed to the network, one or more

hidden layer(s) where data is processed and one

output layer from where results are produced for the

given input. The training process involves giving

known input and target to the network and adjusting

internal parameters viz. weight and biases based on

the performance measure and other network

parameters.

2.2.1 Parameters of Network Selection

Selection of network involves rigorous trial and

error procedures. Mean Square Error (MSE) and

Mean Relative Error (MRE) are two indices which

have been used for the performance measure of the

network. As MSE and MRE are good measures for

indicating the goodness of fit at high and moderate

output values respectively (Karunanithi et al., 1994).

)(

yyMSE −=

∑∑

(2)

100

)(

∑∑

⎟

⎠

⎞

⎜

⎝

⎛

−

MRE

(3)

where, y

(t)

= standardized target value for pattern j,

= output response from the network for pattern j, p

= total number of training pattern; q = number of

output nodes.

Besides the network architecture, momentum

factor and learning rate are also important network

parameters, used to evaluate the network

performance. The network architecture is decided

based on the MRE value as MRE gives more

realistic idea about the predicted output. Therefore,

it plays an important role in network selection. The

value of learning rate η and momentum factor α is

decided after evaluating different combinations. The

learning rate is highly influential for the

convergence of training. If it is too high, then search

may miss a valley in the error surface, on the other

hand if it is too small, the convergence will be very

slow (Chandramouli and Raman, 2001). A

momentum factor, α, is generally used to accelerate

the convergence (Ahmed and Sarma, 2007). An

iterative procedure in combination of different

learning rate and moment factor is adopted to

finalize the number of neurons in the hidden layer.

Burian et al. 2001 stated that typically the

generalization of prediction and accuracy of an

application increase as the number of hidden

neurons decreases; as the number of hidden neurons

IMPORTANCE OF INPUT PARAMETER SELECTION FOR SYNTHETIC STREAMFLOW GENERATION OF

DIFFERENT TIME STEP USING ANN TECHNIQUES

213

increases, there is a corresponding increase in the

number of parameters describing the approximating

functions. Hence the ANN network becomes more

specific to the training data as the neurons in the

hidden layer increases. Generally, in ANN

application the numbers of neurons in the hidden

layer are decided after trial and error for a particular

application. The trial for this study is started with

three neurons in the hidden layer and the network is

studied up to a model with 20 neurons in the hidden

layer. The activation function used for this work is

sigmoid. This function generally takes the

normalized input and target. Therefore

normalization of the data is essential. The inputs and

targets patterns are normalized so that the values fall

in the range of [-1, 1]. The expression used for the

same is given below;

minmax

min

2 −

⎟

⎠

⎞

⎜

⎝

⎛

−

(4)

The tan-sigmoid function is also used for the output

in order to achieve the output values in range of -1 to

1. The obtained output is then un-normalized to get

the predicted target value in the same unit. The

expression for the output of un-normalization is;

pppn

pp min)min)(max1(5.0 +−+=

(5)

where, p

is normalized input, p is actual input min

is minimum value of input vector, max

is maximum

value of the input vector.

2.2.2 ANN Model for Synthetic Streamflow

Generation

In the present study, three layer feed-forward neural

networks is selected. The tan-sigmoid transfer

function is used in hidden layer and output layer

which generate the output value ranging from 0 to 1.

The illustrative neural network architecture is shown

in Fig. 2 which is developed on monthly basis.

Inflow data of the six years (2002-2007) for the

LSHE project has been used in this study, out of

which, 4 years data is used for the training of the

network and 3 years overlapped data are used for the

testing of the network. Since, there are 12 periods

for monthly series, the value of the mean, standard

deviation, average time rate of change of discharge

in different periods of the series (gradient),

maximum and minimum value of historical flow

repeats after each 12 period for the particular

generation. The same is followed for each time step.

The most common and popular multi-layer network

used in training algorithm- Back Propagation (BP)

(Rumelhart et al., 1986 and Hagan et al., 1996) is

adopted in this study.

Inner Layer Hidden Layer Outer layer

Figure 2: ANN architecture for synthetic streamflow

generation.

It is found that a model working well for a

monthly streamflow series does not perform well for

a series having smaller time step discretization such

as ten daily, eight daily, six daily. Therefore it was

decided to attempt different model for different time

step discretization.

Nonlinearity of streamflow series increases with

decrease in the length of time step over which the

values are averaged. Therefore different models

having different number of input parameters have

been tried to obtain the best possible model for a

particular time step length. Different models have

been tried in this study by using different

combinations of input parameter from the following

set of input parameters; streamflow of current period

), streamflow of previous period (I

t-1

), mean (μ

t+1

)

and standard deviation (σ

t+1

) of historical streamflow

of next period, minimum value of inflow from the

given historical record (min

t+1

) and maximum value

of inflow from the given historical record (max

t+1

average time rate of change of discharge of the

series (G

t+1

). A total of seven different combinations

of input parameters were tried. Nomenclature

followed for the ANN model of different time step

is: ANN (time step) DI, where ANN stands for

Artificial Neural Network, D represent day and I

(can varies from 1 to 7) represents a particular trial

combinations of the input parameters. Thus

ANN10D1 represent 10 daily ANN model with 1st

input parameter combination.

Training was initially carried out for 2500

iterations but it was found that there was no

significant improvement in MSE value after 2000

iteration, rather the time requires to train the network

was increasing, hence the network is trained up to

2200 epochs. The MRE value for the testing and

t-1

t+1

min

t+1

max

t+1

p, t+1

NCTA 2011 - International Conference on Neural Computation Theory and Applications

214

training was found separately and network is

selected considering the lowest MRE and MSE

values for the particular number of neurons in

hidden layer. In this study, the best model has been

decided by varying numbers of neurons in hidden

layer from 3 to 10. For each network different

combinations of learning rate η = 0.00, 0.01, 0.02,

0.04, 0.05, 0.07, 0.09, 0.1, 0.2, 0.3, 0.5, 0.7 and 0.9

and momentum factor α = 0.01, 0.02, 0.04, 0.05,

0.07, 0.09, 0.1, 0.2, 0.3, 0.5, 0.7 and 0.9 have been

tried for the final selection of model.

The best value for learning rate η and momentum

factor α was found after extensive trial of different

combination of η and α. Table-1 present the best

ANN models selected for different time step.

2.2.3 Streamflow Generation Model

In this study, after trained and tested network was

simulated to generate the series of synthetic

streamflow, it was found that after several iterations

the network produces the repeated streamflow series.

This may be occurring because of the difference

between actual target values and predicted target

values which leads to the residual series while

training and testing. The statistical analysis of

residual series shows that, it can be adequately

modeled as normally distributed and crosscorrelated

series with zero mean and unit standard deviation

(Ochoa-Rivera et al., 2007). Therefore, it is very

important to introduce random component in the

streamflow generation model to prevent the network

from generating repetitious sequence of streamflow.

A small random component calculated on the basis

of the standard deviation of the observed streamflow

is added to the output produced by the network

(Ahmed and Sarma, 2007). Thus repetitive

generations of streamflow were handled by

introducing a random component ξ

in the model.

Where, ξ

is an independent standard normal random

variable with mean zero and variance unity, σ

is the

standard deviation of observed streamflow of the

corresponding month. Synthetic streamflow series of

hundred years are generated by feeding the known

value of inflow of previous period, inflow of current

period, periodical mean of the historical flow of next

period and periodical standard deviation of the

historical flow of next period, maximum and

minimum of historic flow of next period and average

time rate of change of discharge in different periods

of the series (gradient) of flow. The output of the

model will be the predicted inflow of the succeeding

period and it will serve as input for the next

iteration. If negative flow occurs during synthetic

streamflow generation, would be replaced by the

minimum value of the historic flow for the particular

period (Ahmed and Sarma 2007).

3 RESULTS AND DISCUSSION

Hundred years’ synthetic streamflow series has been

generated using Thomas-Fiering model and ANN-

based models for different combinations of inputs.

The results are compared with the observed

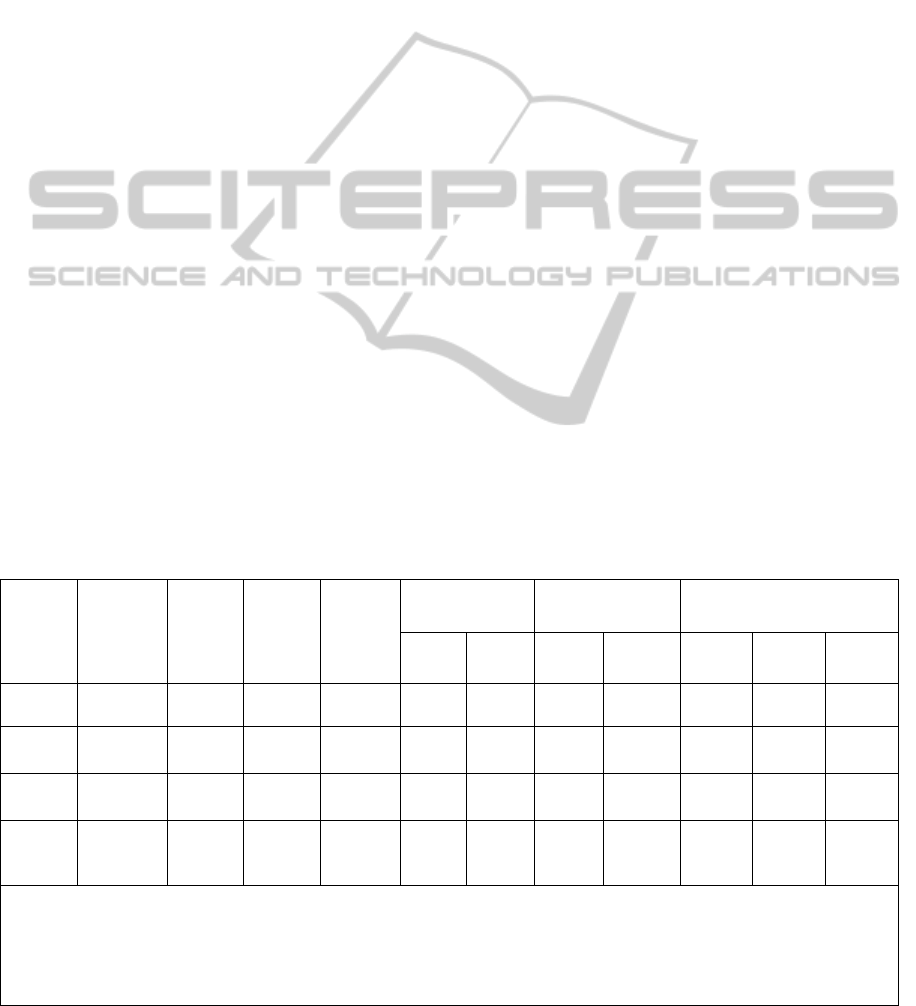
Table 1: Different ANN models selected on the basis of different parameters.

ANN

Model

for

Different

Time

Step

Best Input

Parameters

Number

Neurons

hidden

Layer

Learning

Rate

Moment

Factor

Training Testing Skewness of the Series

MSE MRE MSE MRE Actual

Thomas

Fiering

ANN

ANN30

, μ

t+1

and

t+1

8 0.05 0.05 0.0288 39.6045 0.0636 40.5137 1.3584 1.7089 1.4308

ANN10

t+1

and

t+1

3 0.05 0.50 0.0405 28.2546 0.0580 41.4286 0.9685 1.1984 1.0925

ANN08

, μ

t+1

and

t+1

10 0.04 0.02 0.0323 19.3615 0.0426 30.5810 1.3443 2.1950 1.6550

ANN06

, μ

t+1,

t+1

and G

t+1

8 0.09 0.90 0.0292 19.8986 0.0392 31.6238 1.3548 2.0833 1.9310

Inflow of present time step (I

), Mean of the historical series (μ

t+1

) of next period, Standard deviation of historical series (σ

t+1

) of next

period,

Minimum value of inflow from the given historical record (min

t+1

Maximum value of inflow from the given historical record (max

t+1

) and

Average time rate of change of discharge of the series (G

t+1

)

IMPORTANCE OF INPUT PARAMETER SELECTION FOR SYNTHETIC STREAMFLOW GENERATION OF

DIFFERENT TIME STEP USING ANN TECHNIQUES

215

streamflow series of six years (2002-2007) on the

basis of statistical parameters; periodical mean,

periodical standard deviation and skewness of the

generated and actual observed series and presented

in Table 1. The best ANN model for each of the

different time discretization has been selected based

on the extensive trial carried out with several

combinations of input parameters. The Table 1 gives

the information of each of those models along with

the corresponding parameter for which they are

working best. Several trails has been made to work

out the best ANN model for different time step

discretization by considering different numbers of

hidden neurons and input parameters. 8 neurons in

hidden layer, momentum factor α = 0.05 and

learning rate η = 0.05 was found to be the best for

monthly streamflow generation. Streamflow

generated by ANN series though generates slightly

higher value in case of periodical mean, periodical

standard deviation of the generated series is quite

close to the actual series. The skewness value of the

series generated by ANN30D1 is found closer to the

skewness value of actual series in comparison to that

of the Thomas-Fiering model.

In case of the ten daily ANN models, ANN10D1

is found best. It has 3 neurons in hidden layer (Table

1) with α = 0.5 and η = 0.05. It was observed that

both ANN generated series and Thomas-Fiering

model generated series are in good agreement with

the actual series in respect of periodical mean. In

respect of standard deviations and skewness of the

series, ANN10D1 outperform the Thomas-Fiering

model.

The ANN08D1 having 10 neurons in hidden

layer, α= 0.02 and η = 0.04 is performing better

among others ANN models for eight daily time step.

Periodical mean of the ANN generated series has

been found to give slightly lower values in the pre-

monsoon period and slightly higher value in the dry

period as compared to actual series, but it follows

quite well to the observed series in case of periodical

standard deviation. As observed in the previous

cases regarding Thomas-Fiering model, here also it

can capture the periodical mean very well but it fails

to capture the periodical standard deviation. The

skewness coefficient of the entire series generated

by ANN08D1 is relatively close to skewness value

of the actual streamflow series as compared to the

skewness value of the series generated by Thomas-

Fiering model.

For six daily time step discretization the

ANN06D3 model having four input parameter

(Table 1), 8 neurons in hidden layer, α =0.9 and η

=0.09 found to be the most efficient as compared to

others. The results reveals that though the periodical

mean of the series generated by Thomas–Fierings

methods follows good except for the period during

second seasonal peak i.e. during months of August

and September, the series generated by ANN

predicts relatively low values during pre monsoon

period. On the other hand the periodical standard

deviation of series generated by ANN is in close

agreement with the actual series while the series

generated by Thomas-Fiering model gives very high

values. Moreover, the skewness value of the whole

series generated by Thomas Fiering is also found

higher than the skewness of the actual series as

compared to ANN (Table 1).

4 CONCLUSIONS

The performance of the ANN based model for the

synthetic streamflow generation of the LSHE project

with the limited data set has been investigated and

its comparison is made with the Thomas-Fiering

model considering some statistical parameters viz.

(i) periodical mean, (ii) periodical standard deviation

and (iii) skewness coefficient of the series. The

influence of the time step discretization and

selection of input parameters on the synthetic

generation of streamflow has been evaluated using

both the above said methods. Different models based

on input variables and network parameters have

been tried and the best model for each time step

discretization has been evaluated using above said

three statistical measures. The selection of input

parameters plays an important role in the streamflow

generation. It has been found from the result that the

input parameters which have been working well for

higher time step discretization models did not work

well for the cases of smaller time step discretization.

As the models ANN30D, ANN10D and ANN08D

found better with three input parameters i.e. It, μt+1

and σt+1 while for ANN06D: It, μt+1, σt+1 and

Gt+1; were performing better as compared to three

input parameters. Table 1 presents the best model,

their input variables and the network parameters.

The results of the study depict that: though

periodical mean of the series generated by Thomas-

Fiering follows well to the periodical mean of

observed series as compared to the ANN model in

most of the time discretizations, it gives quite high

values in case of periodical standard deviation as

compare to the ANN generated series.. The

skewness of the series generated by Thomas-Fiering

and ANN models are compared, the skewness of the

ANN generated series is found closer to the

NCTA 2011 - International Conference on Neural Computation Theory and Applications

216

skewness of the observed streamflow series for each

of these time step discretizations. Out the three

performance criteria; (i) periodical mean, (ii)

periodical standard deviation and (iii) skewness

coefficient of the series, ANN was found to be

performing quite well for the periodical standard

deviation and skewness coefficient of the series,

while its performance for periodical mean, was also

found satisfactory and within acceptable limit. Based

on the above analysis, ANN can be regarded as a

competitive alternative method of computing

synthetic streamflow series having potential of better

performance as compared to Thomas-Fiering model.

REFERENCES

Ahmed J A, Sarma A K 2007. Artificial neural network

model for synthetic streamflow generation. Water

Resources Management 21(6):1015-1029

Govindaraju R S 2000. Artificial neural networks in

Hydrology. II: Hydrologic applications. Journal of

Hydrologic Engineering 5(2): 124-137

Bayazıt M 1988. Hidrolojik Modeller, I.T.U. rektorlugu,

Istanbul.

Birikundavyi S, Labib R, Trung H, Rousselle J 2002.

Performance of Neural Networks in Daily Streamflow

Forecasting. Journal of Hydrologic Engineering 7 (5):

392- 398

Box, G E P, Jenkins, G M 1976. Time Series Analysis

Forecasting and Control. San Francisco: Holden-Day

Burian J S, Durrans S R, Nix, S J, Pitt, R E 2001.Training

artificial neural networks to perform rainfall

disaggregation. Journal of Hydrologic Engineering

ASCE 6(1): 43–51

Chandramouli V, Raman H 2001. Multireservoir modeling

with dynamic programming and neural networks.

Journal of Water Resources Planning and

Management 127(2): 89-98

Chandramouli V, Deka P 2005. Neural Network Based

Decision Support Model for Optimal Reservoir

Operation. Water Ressources Management, 19: 447–

464

Diamantopoulou J M, Antonopoulos V Z, Papamichail D

M 2007. Cascade correlation artificial neural networks

for estimating missing monthly values of water quality

parameters in rivers. Water Resources Management

21:649–662

Govindaraju R S, Rao A R 2000. Artificial neural

networks in hydrology. Kluwer Academic Publishers,

Dordrecht

Hagan M T, Demuth H B, Beale M 1996. Neural network

design. PWS/KENT Publishing Co., Boston

Karunanithi N, Grenney W J, Whitley D, Bovee K 1994.

Neural networks for river flow prediction. Journal of

Computing in Civil Engineering ASCE 8 (2):201–220

Kumar D, Raju K, Sathish T 2004. River Flow Forecasting

Using Recurrent Neural Networks. Water Resources

Management, Kluwer Academic Publishers, 18: 143-

161

Loucks D P, Stedinger J R, Haith D A 1981. Water

resources system planning and analysis. Prentice Hall,

Englewood Cliffs, New Jersey

Maass A, Hufschmidt, M M., Dorfman J R, Thomas H A,

Marglin SA, Fair GM 1970. Design of water resources

systems. Harvard University Press, Cambridge

Ochoa-Rivera J C, Andreu J, García-Bartual R 2007.

Influence of Inflows Modeling on Management

Simulation of Water Resources System. Journal of

Water Resources Planning and Management 2:106–

116

Raman H, Sunilkumar N (1995) Multivariate modeling of

water resources time series using artificial neural

networks. Journal of Hydrological Sciences

40(2):145-163

Rumelhart D E, Hinton G E, Williams R J 1986. Learning

internal representations by error propagation,

Parallel distributed processing, Rumelhart DE and

McCleland JL (eds.) vol. 1, Chapter 8, Cambridge,

MA: MIT Press

Srinivasulu S, Jain A 2006. A comparative analysis of

training methods for artificial neural network rainfall–

runoff models. Applied Soft Computing 6: 295–306

Stedinger J R, Taylor, M R 1982. Synthetic streamflow

generation 1: Model verification and validation. Water

Resources Research 18(4): 909–918

Thomas H A, Fiering M B 1962. Mathematical synthesis

of streamflow sequences for the analysis of river

basins by simulation. In: Design of Water Resources

Systems, (Ed. by A. Maas et al.) Chapter 12 Harvard

University Press, Cambridge, Mass

Treiber B, Schultz G A 3/1976. Comparison of required

reservoir storages computed by the Thomas-Fiering

model and the 'Karlsruhe model' Type A and B.

Hydrological Sciences-Bulletin-des Sciences

Hydrologiques- XXI 1(3) 177-185

Yurekli K, Kurunc A. 2004. Performances of Stochastic

Approaches in Generating Low Streamflow Data for

Drought Analysis. Journal of Spatial Hydrology 5(1):

20-32

Zekai Z (6/1978) A mathematical model of monthly flow

sequences. Hydrological Sciences-Bulletin-des

Sciences Hydrologiques 23(2): 223-229

IMPORTANCE OF INPUT PARAMETER SELECTION FOR SYNTHETIC STREAMFLOW GENERATION OF

DIFFERENT TIME STEP USING ANN TECHNIQUES

217