FINDING THE ELECTROMAGNETIC HOMOGENOUS

EQUIVALENT OF THE COMPOSITE MATERIAL USING

GLOBAL OPTIMIZATION TECHNIQUES TO SOLVE THE

INVERSE PROBLEM

Jana Jilková

Dept. of Radar Technology, University of Defence, Kounicova 65, 612 00, Brno, Czech Republic

Keywords: Genetic algorithms, Multi-objective optimization, Composite material, Homogeneous isotropic equivalent

material.

Abstract: The equivalent homogeneous isotropic replacement is computationally efficient way how to enable

simulation of the large numeric models of the composite aircrafts for the purpose of precertification

electromagnetic compatibility tests to estimate the level of their resistance against the lightning. The paper

presents application of two global optimization methods to find an appropriate electromagnetic equivalent

of the composite material by homogeneous material to reduce CPU demands of the numeric models of elec-

trically large airplanes for the purpose of electromagnetic compatibility simulations. First, the inverse

problem is specified using the already known scattering parameters of the composite material. Afterwards,

the global optimization method is applied to find the equivalent with such a value of the complex

electromagnetic permittivity to have the impact on the electromagnetic field propagation as close as possible

to the original composite material.

1 INTRODUCTION

The demands on the important operational cost

reduction of the airplanes by important decrease of

the fuel consumption of today’s airplanes is

nowadays being solved by the aircraft designers

replace replacing the fully metallic skin of airplanes

with composite materials.

Composite material has by its nature lower

shielding effectiveness than the fully metallic skin of

airplanes. As the airplanes operate in the

environment, which is disturbed by large number of

electromagnetic interferences, as nature as artificial,

is necessary to know shielding effectiveness of the

composite structure.

While the airplanes are frequently used to deliver

many people or important cargo, each type of newly

designed airplane has to be tested to prove its

resistance against lightning. While each testing

attempt is very expensive and the whole testing

procedure has to be repeated in case of insufficient

shielding, the numeric simulation to discover the

weak parts is a natural choice. Unfortunately

modelling the composite structures directly causes

the mesh cells to increase, just at the composite

parts. (D'Amore and Sarto, 2000). This is naturally

caused by multilayer structure, tiny structure of the

composites and high frequency range, on which the

EMC values are prescribed by standards.

Composite materials used as construction

materials for aircrafts are most often multilayer

epoxy or polyester resin reinforced by carbon fibres

(carbon fibre reinforced composites CFRC, Von

Klemperer, 2009).

To increase the mechanical toughness and the

electromagnetic shielding, it is possible to introduce

a metallic grid between reinforced epoxy resin layers

(see Figure 1). Unfortunately due to the complicated

structure of the composite materials and as it

contains lossy materials, the numeric models are

becoming even more complicated and more CPU-

time demanding (Sarto, 2002).

One of the approaches to reduce the

computational complexity is to replace the

multilayer structure in numerical model with a

homogeneous isotropic equivalent providing the

same or very close behaviour in electromagnetic

field as the original composite structure. The

324

Jilková J..

FINDING THE ELECTROMAGNETIC HOMOGENOUS EQUIVALENT OF THE COMPOSITE MATERIAL USING GLOBAL OPTIMIZATION TECHNI-

QUES TO SOLVE THE INVERSE PROBLEM.

DOI: 10.5220/0003674903240328

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 324-328

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

homogeneous equivalent in numerical models can be

covered by more sparse mesh net leading to the

lower CPU demands causing the CPU time of the

simulation are reduced. To solve these issues, the

global optimization methods were applied to find

such a value of the complex permittivity of a

homogeneous dielectric layer that exhibits similar

frequency responses of scattering parameters as the

composite material.

In the first part the 3D model of composite

material simulated in commercial full-wave CST

Microwave Studio (CST MWS) is described and its

scattering parameters are calculated to be used as the

input value for the optimization process.

In the second part the principle of the inverse

problem used for the determination of complex

permittivity of the homogeneous material is

described.

In the third part, the design of the global

optimization methods is described. The

implementation details together with the impact of

the selected method using single representative of

single-objective and one of the multi-objective

approach is discussed.

2 SCATTERING PARAMETERS

OF COMPOSITE MATERIAL

The polymer composite supported by carbon fibres

is reported to be the most frequently used material

for aircraft construction. To increase its mechanical

robustness and electromagnetic shielding level the

metallic grid is frequently introduced into the

composite. From the perspective of electromagnetic

parameters, conductive carbon fibres are strongly

anisotropic so they have different parameters in

various axes. Practically this increases the numeric

model complexity even more.

The three-dimensional numeric model of such

composite material was created in a commercial

modelling program CST Microwave Studio (see

Figure 1) consisting of polymer matrix with

thickness of 2 mm, with relative permittivity 4 and

conductivity 0 S/m and a carbon fibre matrix with 35

m in diameter, conductivity set to 10

S/m along

the fibre 50 S/m across fibre and relative

permittivity set to 2.

The model consisted of two such layers of

polymer-carbon composite surrounding a copper

grid with wire 0.3 mm in diameter and eye size

3x1.5 mm.

The whole structure was placed to the standard

R100 waveguide and simulated for normal incidence

of TM

wave. This arrangement was particularly

selected so that the model could have been easily

verified experimentally by direct measurement.

Figure 1: Detailed three dimensional model of carbon fibre

reinforced composite (CFRC) simulated in CST

Microwave Studio.

The high computational demands (from 3 day up

to one week depending on the hardware) on the

simulation solver are not only caused by the

multilayer thin structure of the model, small eye size

of metallic grid and carbon fibres matrix or by

anisotropic nature of the carbon fibres but also by

quite huge frequency range, required for the

precertification test.

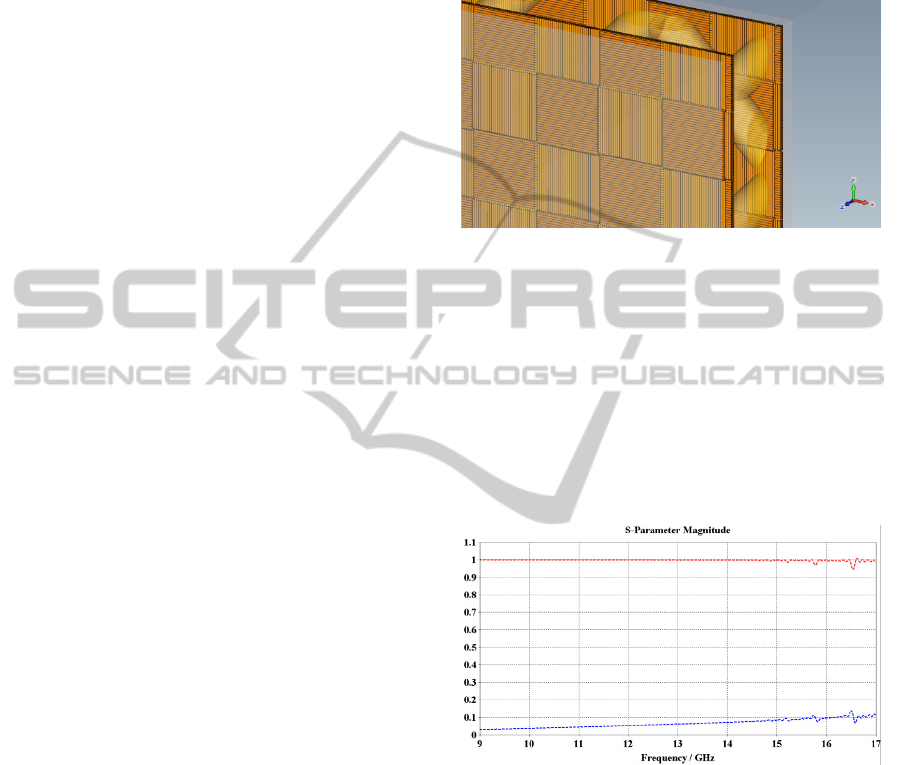
Figure 2: Scattering parameters of composite material: red

line – reflection coefficient, blue line – transmission

coefficient (simulated in CST MWS).

This wide frequency range also has a negative

impact to the overall error of the numeric model.

This challenge was described in the paper (Jilková

and Raida, 2009). The output of the simulation – set

of so called scattering parameters of scattering

parameters (see Figure 2) – served as the input

values to the optimization process.

FINDING THE ELECTROMAGNETIC HOMOGENOUS EQUIVALENT OF THE COMPOSITE MATERIAL USING

GLOBAL OPTIMIZATION TECHNIQUES TO SOLVE THE INVERSE PROBLEM

325

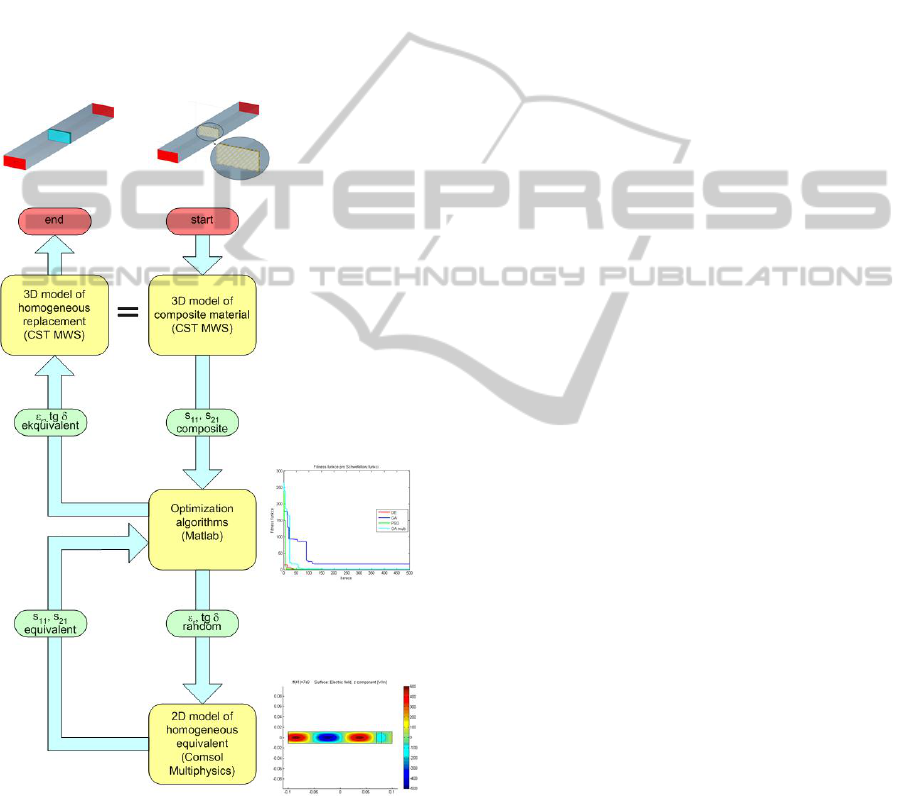
3 PRINCIPLE OF INVERSE

PROBLEM

To find the homogeneous equivalent material two

particular members of the global optimization

methods was used. The inverse problem is specified

as finding such a frequency dependency of the

complex permittivity of a homogeneous dielectric

layer that exhibits similar frequency responses of

both scattering parameters as the composite material

reflection coefficient and s

transmission

coefficient). Replacement principle is shown on

Figure 3.

Figure 3: Principle of inverse problem.

To achieve be able to apply the global

optimization method on this problem, the 2D

problem of the homogeneous dielectrics was created

which was further easier to simulate because of

lower computational demands being therefore

convenient for the optimization. As for the 3D

model, the output of the 2D model consisted of both

scattering parameters that were afterwards compared

with those obtained from 3D model. The input to the

2D model was formed by the the real part of the

relative permittivity and a loss tangent parameter.

These two can be used to calculate so called

complex permittivity that completely characterizes

any lossy dielectric material. The model was created

in COMSOL Multiphysics. For the purpose of the

global optimization, the dielectric constant was

permitted to vary within the interval [1; 1000] and

the loss tangent was set to vary within [0; 1000].

The complex permittivity acquired from the

optimization of the 2D model was finally verified in

the 3D model of the equivalent in CST MWS to see

if the scattering parameters match in the whole

frequency spectra.

4 GLOBAL OPTIMIZATION

Why should the global optimization methods be

used to find an equivalent homogeneous material?

An usual way how to find properties of equivalent

material is to derive its properties using the

analytical description of its electromagnetic

properties.

This involves expressing the characteristics of

the material in Maxwell equations which may

become very complicated when it comes for

complex multilayer lossy anisotropic structure. The

usual way how to cope with it is to introduce some

approximation and simplifications which can be

limiting in many ways.

Also the analytic solution may change heavily if

some parameters of the model change (eg.

introducing nonzero conductivity of the dielectric to

take into account its non-zero loss). On the other

hand using the optimization methods in connection

with numerical models enables finding equivalent

material of much broader range of composite

structures since the only requirement for the

structure is that it has to be possible to reliably

simulate.

The principle stays the same for simple layer

composite, for multilayer composite structure, for

single carbon fibres or for knitted carbon armature.

The method is even convenient for composite

structures with metallic grid.

For the entire frequency range, a single

evaluation of the relative permittivity and a single

evaluation of the loss tangent are required (see Table

1). The fitness function is of the form:

(x) = [ S

ref

- S

(x)]

-1

(1)

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

326

(x) = [ S

ref

– S

(x)]

-1/2

(2)

Here, S

11,ref

is the computed value of the reflection

coefficient of the realistic model of the composite

material at the frequency range. Then, S

11,opt

(x) is the

reflection coefficient of the equivalent homogeneous

material computed in COMSOL Multiphysics for

the vector of state variables x = [



, tan



Similarly, S

21,ref

is the computed transmission

coefficient of the realistic model of the composite

material, S

21,opt

(x) is the transmission coefficient of

the equivalent homogeneous material computed in

COMSOLl Multiphysics for the state vector x = [



tan



]

The equivalent material was searched for one

particular composite material using two different

optimization approaches – a singleobjective and a

multiobjective. For the single-objective solution, the

fitness functions (1) and (2) are weighted by

weighting coefficients w

= 1 and w

= 1 and

summed:

F(x) = w

(x) + w

(x) (3)

4.1 Single-objective Optimization

For single-objective optimization a classical global

optimization representative – a genetic algorithm –

was selected. Genetic Algorithms (GA) are members

of stochastic global optimization methods and are

based on the Darwinian Theory of the evolution of

species. The values of the control parameters were

chosen according to recommendations published in

(Rahmat-Samii and Michielssen, 1999).

The population consisted of 50 individuals, the

accuracy of binary coding was set to 0.001. Indivi-

duals for the next population were selected by the

tournament operator. Probability of the multi-point

crossover was set to 70 % and probability of the

multi-point mutation was set to 6 %. The elitist

strategy was applied. The optimization was set to

minimize the optimized problem.

Time needed for a single simulation run and then

calculation of the complex permittivity value using

single-objective genetic algorithm was

approximately 12 hours (see Table 1). Because of

time needed for the calculation of the criteria

function, the entire optimization cycle was repeated

only one hundred times.

The values of complex permittivity obtained

from the optimization run were then set to 3D model

to compare the reflection parameters with the model

of the original composite. The error of calculation

was at maximum 0.45% on the whole frequency

range of 15-40 GHz.

In Table 1 one chosen value of complex

permittivity from the set of the optimization run is

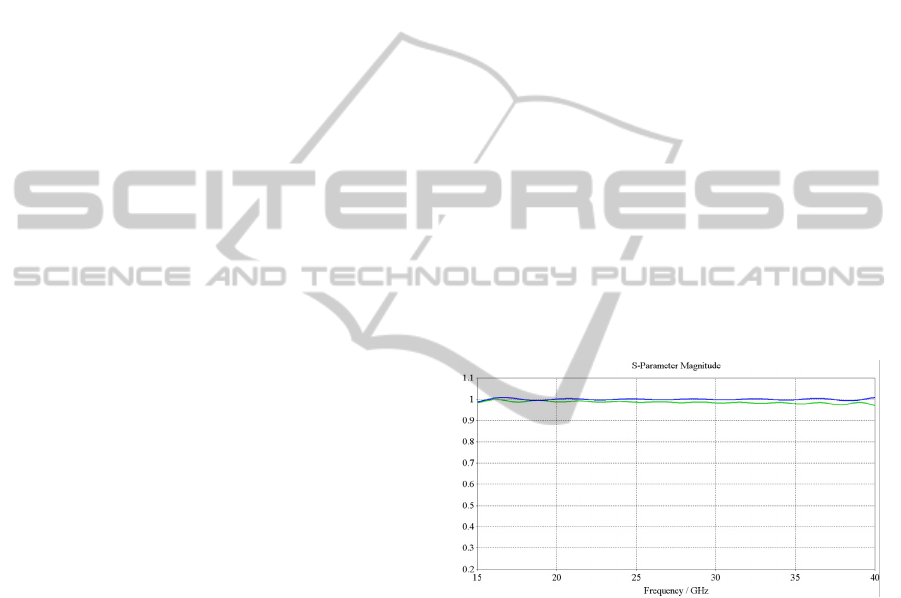
shown. On Figure 4, the scattering parameters for

this value of the complex permittivity of the

homogeneous replacement are shown in comparison

with scattering parameters of the original composite.

As it can be seen on Figure 4 good match was

achieved.

4.2 Multi-objective Optimization

Niched-Pareto Genetic Algorithms, by Horn et al., is

a multi-objective GA based on the non-domination

concept. NPGA uses the binary tournament selection

(Deb, 2001).

The population consisted of 50 individuals,

mutation probability was set to 6%, the crossover

probability was 70% and the selected accuracy of

coding is 0.001.

The result of a single optimization run is formed

by a set of results corresponding to all the criterions

(Pareto front). The calculation needed to evaluate

one Pareto front was about half of the time needed

for single-objective optimization (see Table 1), the

optimization run was repeated hundred times.

Figure 4: Reflection coefficients of replacements achieved

by single-objective genetic algorithms (blue) in

comparison with the detailed 3D composite model (green).

After an inverse implementation of the values of

complex permittivity of replacements from all

simulation runs to the 3D model, all the optimized

results were simulated to do the comparison with the

original composite material results.

In Table 1 it is shown, that maximal error of the

replacement on frequency range 15 – 40 GHz is less

then 0.45 %.

On Figure 5 a single choice value of the complex

permittivity of the replacement compared with

reflection coefficient of the original composite

material is shown.

FINDING THE ELECTROMAGNETIC HOMOGENOUS EQUIVALENT OF THE COMPOSITE MATERIAL USING

GLOBAL OPTIMIZATION TECHNIQUES TO SOLVE THE INVERSE PROBLEM

327

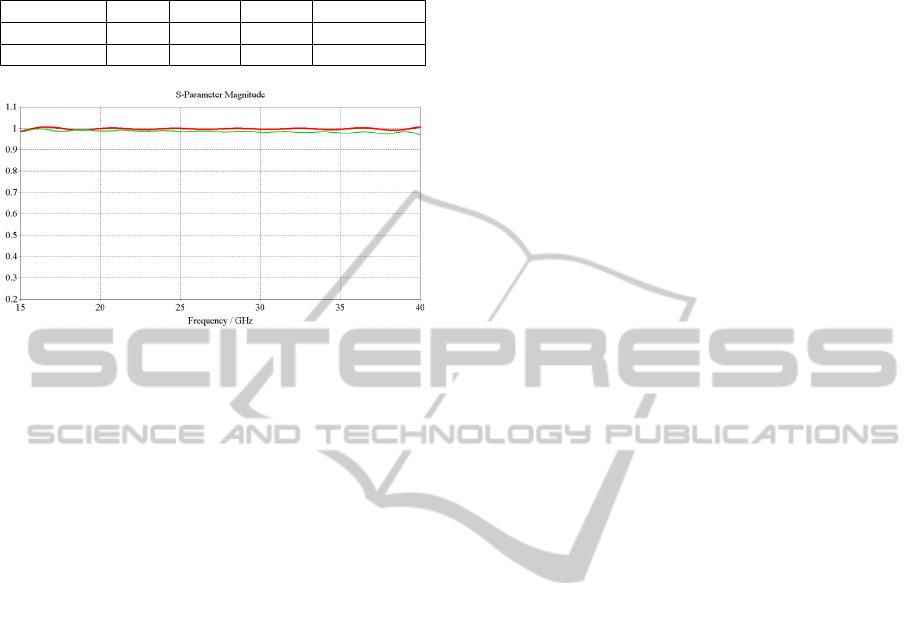
Table 1: Comparison of optimization methods, minimum

and maximum accuracy reached for frequency range 15-

40 GHz.

Optimization ε

[-] tg δ [-] time [h] Accuracy [%]

GA 36.64 549.34 12 0.16-0.45

NPGA 80.27 726.73 6 0.06-0.45

Figure 5: Reflection coefficients of replacements achieved

by multi-objective NPGA in comparison with originally

reflection coefficient of composite material. Green linie:

composite material, red linie: NPGA replacement.

Simulated in CST MWS.

5 CONCLUSIONS

For the comparison, the single-objective

optimization (reflection coefficient considered) and

the multi-objective optimization (both the reflection

coefficient and the transmission one) were tested.

In order to compute the minima of objective

functions, genetic algorithms and Niched-Pareto

genetic algorithm were applied to the problem. First,

the single-objective approach exhibits a very good

functionality. Second, the substitute synthesized by

the multi-objective approach shows a very good

agreement too.

The most significant advantage of the multi-

objective approach is the speed of the simulation.

Time needed to one simulation for NPGA was one

half compared to single-objective approaches.

REFERENCES

Von Klemperer, C. J., Maharaj, D., Composite

electromagnetic interference shielding materials for

aerospace applications. Compos. Struct. (2009),

doi:10.1016/j.compstruct.2009.04.013.

Sarto, M. S., Sub-cell Model of Multilayer Composite

Materials for Full FDTD and Hybrid MFIE/FDTD

Analyses. In IEEE International Symposium on

Electromagnetic Compatibility, 2002. EMC 2002.

Volume 2, Issue, 19.-23. Aug. 2002. Pages 737-742.

ISBN: 0-7803-7264-6.

D'Amore, M., Sarto, M. S., Theoretical and Experimental

Characterisation of the EMP-Interaction with

Composite-Metallic Enclosures. IEEE Transaction on

electromagnetic Compatibility, vol. 42, No. 1,

February 2000.

Jilková, J., Raida, Z., Genetic Homogenization of

Composite Materials. Radioengineering, 2009, vol.

18, No. 1, p. 34-37. ISSN: 1210-2512.

Deb, K., Multi-Objective Optimization using Evolutionary

algorithms. John Wiley and Sons, 2001. ISBN 0-471-

87339-X.

Rahmat-Samii, Y., Michielssen, E., Electromagnetic

Optimization by Genetic Algorithms. New York: J.

Wiley and Sons, 1999.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

328