VALIDATED MODEL OF A PRESSURE MICROPROBE FOR

WATER RELATIONS OF PLANT CELLS

Victor Bertucci-Neto and Paulo Estevão Cruvinel

Embrapa Instrumentação Agropecuária, Rua XV de Novembro, 1452,13560-970, São Carlos, SP, Brazil

Keywords: Model vegetable cell, Pressure probe, Instrument turgor.

Abstract: Turgor pressure is a physiologic variable of fundamental importance. It is a component of water potential

and a measure of water status in a plant. For a long time direct measurement of turgor pressure was not

possible. Three decades ago a pressure probe technique was originally introduced to measure turgor

pressure and water relations of higher plant cells. Early experiments were made with a glass capillary linked

to a pressure chamber, filled with silicone oil. After the vegetable cell to be punctured with the tip of the

capillary, a sensor was used to measure the pressure in the chamber. From then until now the usual

procedure has been to detect the meniscus position at the moment that the cell is punctured and manually, or

automatically, to return the meniscus to the original position. When this occurs the pressure in the chamber

is measured with a sensor. Some attempts were made to get the instrument automated but there is no

systematic description about it. Based on this, it is proposed a dynamic model for the hydraulic system that

can be helpful to design a closed loop system aiming an automated instrument. It is also shown that the

theoretical model reasonably matches the experimental results.

1 INTRODUCTION

Turgor pressure is a physiologic variable of

fundamental importance. It is a component of water

potential and a measure of water status in a plant.

For mature, turgid cells of higher plants, changes of

water potential are largely reflected in changes of

turgor. For a long time, the direct measurement of

turgor was not possible (Steudle, 1993). Three

decades ago a pressure probe technique was

originally introduced to measure turgor and water

relations of higher plant cells (Husken et al., 1978).

Early experiments were made with a glass capillary

linked to a pressure chamber, filled with silicone oil.

After the vegetable cell to be punctured with the tip

of the capillary, a sensor was used to measure the

pressure in the chamber. Later, it was remarked that

a necessary condition for constructing cell pressure

probes is given by:

inol

(1)

where V

and V

are the internal volumes of the cell

and apparatus respectively, B is the elastic

coefficient of the cell, and c

is the coefficient of

compressibility of the oil. The condition imposed by

Figure 1: Schematic diagram of a pressure microprobe.

Equation (1) indicates that V

must be reduced in

several orders of magnitude, and the meniscus

formed at the tip of the capillary must be used as a

reference of measurement. From then to now the

usual procedure has been to detect the meniscus

position at the moment that the cell is punctured

manually, or automatically, to return the meniscus to

the original position. When this occurs the pressure

in the chamber is measured with a sensor. In the

Figure 1 is shown a schematic diagram representing

433

Bertucci-Neto V. and Estevão Cruvinel P..

VALIDATED MODEL OF A PRESSURE MICROPROBE FOR WATER RELATIONS OF PLANT CELLS.

DOI: 10.5220/0003539704330436

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 433-436

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

the pressure probe acting on a cell, with the

meniscus being observed by the microscope and

video camera. After the image treatment, the signal

equivalent to the meniscus position is sent to the

controller. The controller acts on the motor and

reducing gear causing the movement of the piston

returning the meniscus to the original position. Some

attempts were made to get the instrument automated

(Husken et al., 1978, and Cosgrove and Durachko,

1986) but there is no systematic description about it.

Manual measurements can be made during short

times but it can be difficult if one wants to register

long term behaviour. Moreover, manual operation is

based on the operator skill and in the subjective

interpretation of the image. By the other hand,

control system algorithms can be more easily

designed and implemented when the system plant is

reasonably known. Based on this, it is proposed a

dynamic model for the hydraulic system that can be

helpful to design a closed loop system aiming an

automated instrument. In addition, the mathematical

model can be useful to understand the contribution

of each physical parameter to the measurement

performance.

2 SYSTEM MODELLING

The system modelling is based on the analysis of

pipe flow. It is considered a cylindrical element

(radius=r, and length=L) in a pipeline and expressed

the loss in pressure due to the forces acting on the

fluid. Balancing the forces in terms of the pressure p

along the longitudinal axis y, including the retarding

force due to the shear stress τ

gives:

()

[]

()()

dyrrdppp

πτπ

=+−

(2)

resulting in:

=−

(3)

Integrating both sides of Equation (3) from the

pressure at the downstream end to the upstream end,

and along the length of the element, yields the

amount in pressure Δp that droped:

=Δ

(4)

Last equation shows the relation between shear

stress and the pressure drop. Δp can be equated to

the specific weight γ=ρg (density multiplied by

gravity acceleration) multiplied by the heading loss

. Then Equation (4) can be rewritten:

(5)

In the case of laminar flow in the pipe Newton’s law

of viscosity can be written as τ

being proportional

to the velocity gradient v related to the radius, with

constant of proportionality defined as the coefficient

of viscosity μ. Then Equation (5) can be written:

−==

(6)

Integrating last equation from the maximum velocity

(at the center of the pipe) to v, and from 0 to r,

becomes:

−=

(7)

Last equation shows that the velocity profile is a

parabolic curve. When r=0, v=v

. Substituting v=0,

and r=d

/2 (d

is the tube diameter), and considering

=2V, being V the mean velocity, then:

(8)

showing that the head loss is proportional to the

mean velocity. By setting Equation (8) equal to

Darcy’s equation (Vennard, 1961) it can be derived

an expression for the friction factor for laminar pipe

flow:

(9)

By the other hand, multiplying both sides of Darcy’s

equation by

g and equating to the same pressure

drop h

obtained in Equation (5):

fhp

ρττργ

=⇒===Δ

(10)

Using the friction factor given in the Equation (9)

and substituting in the last equation it is obtained an

expression that relates the shear stress to the

velocity, or:

(11)

The analysis that follows is described in Doebelin

(1990) that considered a gas system with tube

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

434

volume a small fraction of chamber volume.

However the flow considered here is liquid causing

a simplification because the spring effect that exists

due to the gas flow is negligible in liquid flow case.

Analysis consists of applying Newton’s law by

balancing the forces along the tube in the

longitudinal axis y. Initially is considered that

an initial arbitrary value) when p

changes slightly in some way. Then it is considered

at this point that p

and p

mean the excess pressures

over and above p

. The force f

due to the pressure p

is given by:

Apf

(12)

The viscous force f

due to the wall shearing stress is

given by the division of Equation (11) by the area of

the pipe wall:

yLVLf



πμπμ

88 ==

(13)

where y

is the liquid displacement due to p

action.

This displacement causes a volume change

=πd

/4 and pressure excess p

=πBd

/(4V

)

(B is the elastic coefficient). The equivalent force is

given by:

yBd

(14)

Applying Newton’s law along the longitudinal axis

implies to balance the forces and equate to the fluid

mass m multiplied by the acceleration a, or:

amfff

mvi

⋅

−−

(15)

Above equation is useful for uniform velocity

distribution. However, the quadratic velocity profile

verified in Equation (7) indicates that a correction

factor must be used in the right side of Equation

(15). In this case the quantity m.a must be multiplied

by 4/3. Then, Equation (15) can be rewritten as:

yLp



316

ρπ

πμ

=−−

(16)

Applying Laplace transform in Equation (16) yields:

()

(17)

Last equation relates the displacement of the

meniscus due to the pressure applied at the tip of the

capillary. Moreover, it permits an evaluation of the

dynamical behaviour by the variation of its physical

parameters.

3 EXPERIMENTAL SET UP AND

COMPARISON

The meniscus was observed with a video camera

coupled to a microscope. The video signal was

sampled at 70 ms and digitalized with a video board

installed in the personal computer. It was developed

a software based on Imaq Vision for LabView for the

meniscus detection. This software is based on

pattern recognition and gives as result the number of

pixels (Npixel) concerning to the previously chosen

initial position. It was coupled a “T” connection at

the tip of the capillary. The capillary was previously

filled with silicone oil. It was linked at one of the

inputs of the T connection an air duct supplied by an

air compressor. At the other input was coupled a

pressure sensor with reading rate equal to 10mV/psi.

After the air compressor to be switched on, the

readings of both meniscus position, and voltage

signal due to the sensor were collected and stored in

the computer. In the Figure 2 is shown the curve due

to the meniscus displacement (in Npixel) and the

curve due to the voltage signal in the pressure

sensor. It can be seen in Equation (17) that the final

value is L/B. This means that if the length L is

increased then the meniscus displacement is also

increased. It was used the following values for each

physical parameter in the Equation (17), with B, µ,

and ρ being attributed to the silicone oil, and L

chosen according to the optical resolution: L=0.15m;

=270 10

-6

m; ρ=900 Kg/m

;

B=2.18 10

N/m

;

μ=10

-3

Kg/m s. Substituting the above values results

in:

10.074.88.365

10556.5

)(

+⋅+

⋅

−

(18)

To compare the mathematical model to the

experimental response it is necessary to transform

the pressure sensor signal measured in volt in

pressure dimension. Then, the voltage signal must be

multiplied by (1/0.6mV) x psi, with 1psi=6894.6

N/m

. The relation between the meniscus

displacement in meter and Npixel was previously

measured with a rule adapted in the microscope lens.

It was found 1 pixel=1/6.36x10

m. Applying the

transformed input pressure signal to the Equation

VALIDATED MODEL OF A PRESSURE MICROPROBE FOR WATER RELATIONS OF PLANT CELLS

435

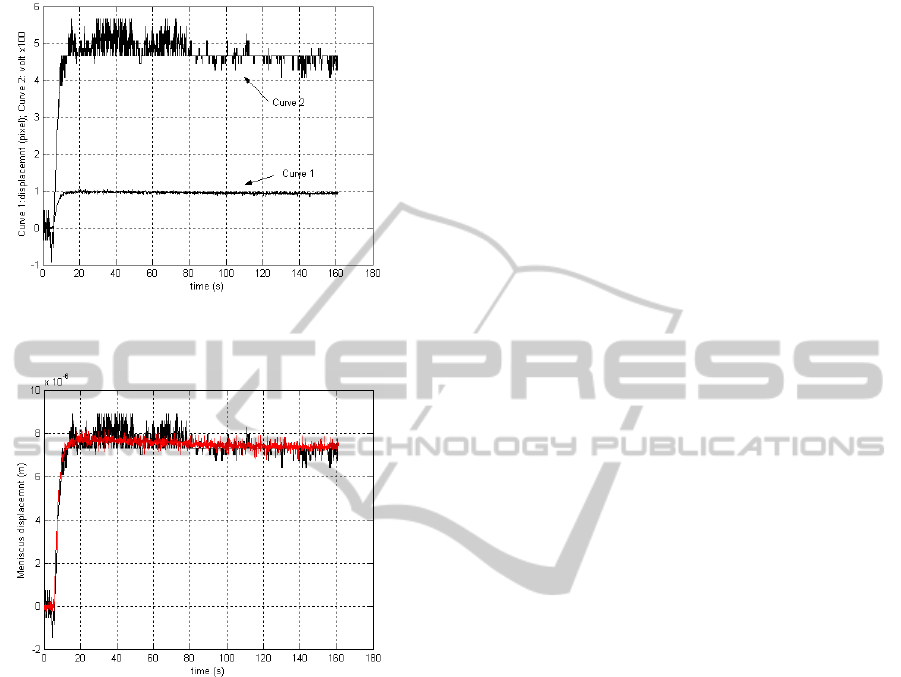
(18) results in the red curve showed in Figure 3. This

same figure shows the experimental curve.

Figure 2: Curve 1: meniscus displacement (Npixel). Curve

2: pressure sensor signal (volt x 100).

Figure 3: Meniscus displacement: experimental response

(black), and theoretical response (red).

4 CONCLUSIONS

Despite the noisy signal imposed by the meniscus

detection (mean=0.47 Npixel and variance=0.10

Npixel

) it can be seen in Figure 3 the strong

accordance between the theoretical and experimental

responses. The mathematical model could match the

dynamical behaviour and the steady state exhibited

in the experimental response. It was not considered

in the modelling the effects of the surface tension

and the glass compressibility because the magnitude

of both of them were previously known as

negligible. Experimental results show that the

proposed model can be applied in open and closed

loop designs according to the operation needs

(manual or automated). The modelling is also

justified in the evaluation of the contribution of each

physical parameter to the system response. This

permits to predict the importance of using high or

low viscosity silicone oil, a long or short pipe, or the

more or less compressible oil. All of these

considerations will be related to the system range

and performance.

ACKNOWLEDGEMENTS

This work was supported by Embrapa.

REFERENCES

Bertucci-Neto, V. 2005. Modelagem e automação em nova

técnica de medida para relações de água e planta.

Thesis (in portuguese). Escola de Engenharia de São

Carlos, Universidade de São Paulo. São Carlos.

Cosgrove, D. J.; Durachko, D. M. 1986. Automated

pressure probe for measurement of water transport

properties of higher plant cells. Review of Scientific

Instrument. v.57. n.10. p.2614-2619.

Doebelin, E. O. 1990. Measurement systems application

and design. 4. ed. New York: McGraw-Hill Publishing

Company.

Husken, D.; Steudle, E.; Zimmermann, U. 1978. Pressure

probe technique for measuring water relations of cells

in higher plants. Plant Physiology. v. 61. p. 158-163.

Steudle, E. 1993. Pressure probe technique: basic

principles and application to studies of water and

solute relations at the cell, tissue and organ level. Ed.

J. A. C. Smith and H. Griffiths . Oxford, UK: Bios

Scientific Publishers Ltd. p.5-36.

Vennard, J. K. (1961). Elementary fluid dynamics. 4. ed.

New York: John Wiley and Sons, Inc.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

436