OPTIMIZATION LEARNING METHOD FOR DISCRETE

PROCESS CONTROL

Ewa Dudek-Dyduch and Edyta Kucharska

Institute of Automatics, AGH University of Science and Technology, al. Mickiewicza 30, PL 30-059 Krakow, Poland

Keywords: Discrete Manufacturing Processes Control, Optimization Method, Learning Algorithm.

Abstract: The aim of the paper is to present a novel conception of the optimization method for discrete manufacturing

processes control. This method uses gathering information during the search process and a sophisticated

structure of local optimization task. It is a learning method of a special type. A general formal model of a

vast class of discrete manufacturing processes (DMP) is given. The model is a basis for learning algorithms.

To illustrate the presented ideas, the scheduling algorithm for a special NP-hard problem is given.

1 INTRODUCTION

The control of Discrete Manufacturing Process

(DMP) lies in determining the manner of performing

a certain set of jobs under restrictions referring to

machines/devices, resources, energy, time,

transportation possibilities, order of operation

performing and others. Most of control algorithms

are approximate (heuristic) due to NP-hardness of

the optimization problems. Within the frame of

artificial intelligence, one attempts at both formal

elucidation of heuristic algorithm ideas and giving

some rules for creating them (metaheuristics)

(Dudek-Dyduch and Fuchs-Seliger, 1993),

(Dudek-Dyduch and Dyduch, 1988), (Pearl, 1988),

and (Rajedran, 1994). The paper ties in with this

direction of research. It deals with formal modeling

of discrete manufacturing/production processes and

its applications for control/planning algorithms. It

presents the development of ideas given in

(Dudek-Dyduch, 2000). Its aim is twofold:

 To present a novel heuristic method that uses

a sophisticated local optimization and

gathering information during consecutive

search iterations (learning method);

 To present an intelligent search algorithm

based on the method for a certain NP-hard

scheduling problem, namely a scheduling

problem with state depended retooling.

The paper uses the formal model based on

the special type of the multistage decision process

given below.

2 FORMAL MODEL OF DMP

Simulation aimed at scheduling any DMP consists in

determining a sequence of process states and the

related time instances. The new state and its time

instant depend on the previous state and the decision

that has been realized (taken) then. The decision

determines the job to be performed, resources,

transport unit, etc. Manufacturing processes belong

to the larger class of discrete processes, namely

discrete deterministic processes (DDP). The formal

model of DDP given in (Dudek-Dyduch, 1990),

(Dudek-Dyduch, 1992), and (Dudek-Dyduch, 1993)

will be adopted here for DMP.

Definition 1. A discrete manufacturing/pro-

duction process (DMP) is a process that is defined

by the sextuple DMP=(U, S, s

, f, S

, S

) where U is

a set of control decisions or control signals, S=X×T

is a set named a set of generalized states, X is a set

of proper states, T





{0} is a subset of non

negative real numbers representing the time

instants, f:U×S



S is a partial function called

a transition function, (it does not have to be

determined for all elements of the set U×S),

=(x

), S



S, S



S are respectively: an initial

generalized state, a set of not admissible generalized

states, and a set of goal generalized states, i.e.

the states in which we want the process to take place

at the end.

It can be noticed, that DMP corresponds to some

multistage decision processes.

Dudek-Dyduch E. and Kucharska E..

OPTIMIZATION LEARNING METHOD FOR DISCRETE PROCESS CONTROL.

DOI: 10.5220/0003532400240033

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 24-33

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

The transition function is defined by means of

two functions, f=(f

) where f

U×X×T



determines the next state, f

U×X×T



T determines

the next time instant. It is assumed that the

difference



t =f

(u, x, t)-t has a value that is both

finite and positive.

Thus, as a result of the decision u that is taken or

realized at the proper state x and the moment t, the

state of the process changes for x’=f

(u, x, t) that is

observed at the moment t’=f

(u, x, t)=t+



Because not all decisions defined formally make

sense in certain situations, the transition function f is

defined as a partial one. As a result, all limitations

concerning the control decisions in a given state s

can be defined in a convenient way by means of so-

called sets of possible decisions U

(s), and defined

as: U

(s)={u



U: (u, s)



Dom f}.

At the same time, a DMP is represented by a set

of its trajectories that starts from the initial state s

. It

is assumed that no state of a trajectory, apart from

the last one, may belong to the set S

or has

an empty set of possible decisions. Only a trajectory

that ends in the set of goal states is admissible.

The control sequence determining an admissible

trajectory is an admissible control sequence

(decision sequence). The task of optimization lies in

the fact of finding such an admissible decision

sequence ũ that would minimize a certain criterion

In the most general case, sets U and X may be

presented as a Cartesian product U=U

×U

×...×U

X=X

×X

×...×X

i.e. u=(u

,...,u

), x=(x

,...,x

There are no limitations imposed on the sets; in

particular they do not have to be numerical. Thus

values of particular co-ordinates of a state may be

names of elements (symbols) as well as some

objects (e.g. finite set, sequence etc.). Particular u

represent separate decisions that must or may be

taken at the same time. The sets S

, S

, and U

are

formally defined with the use of logical formulae.

Therefore, the complete model constitutes

a specialized form of a knowledge-based model

(logic-algebraic model). According to its structure,

the knowledge on DMP is represented by coded

information on U, S, s

, f, S

, S

. Function f may be

defined by means of a procedure or by means of

IF..THEN rules. The basic structure of DMP (def.1)

is usually created on the basis of process technology

description. Based on additional expert knowledge

(or analysis of DMP) subsets of states can be

differentiated, for which best decisions or some

decision choice rules R (control rules) are known.

3 OPTIMIZATION LEARNING

METHOD

The method of solution search with information

gathering is a significant development of the method

presented in papers (Dudek-Dyduch, 1990),

(Dudek-Dyduch, 2000), which generates subsequent

process trajectories with the use of previously

obtained and analyzed solutions (admissible and

non-admissible trajectories) so as to generate

improved solutions.

The method uses local optimization tasks.

The task lies in the choice of such a decision among

the set of possibilities in the given state U

(s), for

which the value of a specially constructed local

criterion is the lowest. The form of the local

criterion and its parameters are modified in

the process of solution search.

The local criterion consists of three parts and is

created in the following way. The first part concerns

the value of the global index of quality for the

generated trajectory. It consists of the increase of the

quality index resulting from the realization of the

considered decision and the value related to the

estimation of the quality index for the final

trajectory section, which follows the possible

realization of the considered decision. This part of

the criterion is suitable for problems, whose quality

criterion is additively separable and monotonically

ascending along the trajectory (Dudek-Dyduch,

1990).

The second part consists of components related

to additional limitations or requirements.

The components estimate the distance in the state

space between the state in which the considered

decision has been taken and the states belonging to

the set of non-admissible states S

, as well as

unfavorable states or distinguished favorable states.

Since the results of the decision are known no

further than for one step ahead, it is necessary to

introduce the “measure of distance” in the set of

states, which will aid to define this distance. For that

purpose, any semimetrics can be applied. As we

know, semimetrics, represented here as



, differs

from metrics in that it does not have to fulfill

the condition



(a,b)=0



a=b.

The third part includes components responsible

for the preference of certain types of decisions

resulting from problem analysis. The basic form of

the criterion q(u,x,t) can be then represented as

follows:

q(u,x,t)=



Q(u,x,t)+̂Q(u,x,t)+



(u,x,t)+…+a



(u,x,t)+…+a



(u,x,t)+



(u,x,t)+…+b



(u,x,t)+…+ b



(u,x,t)

(1)

OPTIMIZATION LEARNING METHOD FOR DISCRETE PROCESS CONTROL

where:





Q(u,x,t) - increase of the quality index value

as a result of decision u, undertaken in

the state s=(x,t);

 ˆQ(u,x,t) - estimation of the quality index value

for the final trajectory section after

the decision u has been realized;





(u,x,t) - component reflecting additional

limitations or additional requirements in

the space of states, i=1,2,...,n;

 a

- coefficient, which defines the weight of i-th

component



(u,x,t) in the criterion q(u,x,t);





(u,x,t) - component responsible for

the preference of certain types of decisions,

j=1,2,...,m;

 b

- coefficient, which defines the weight of j-th

component responsibles for the preference of

particular decision types.

The significance of particular local criterion

components may vary. The more significant a given

component is, the higher value is of its coefficient. It

is difficult to define optimal weights a priori. They

depend both on the considered optimization problem

as well as the input date for the particular

optimization task (instance). The knowledge

collected in the course of experiments may be used

to verify these coefficients. On the other hand,

coefficient values established for the best trajectory

represent aggregated knowledge obtained in

the course of experiments.

The presented method consists in the

consecutive construction of whole trajectories,

whilst their generation always begins from the initial

state s

=(x

). For each generated trajectory, both

admissible and non-admissible, its final

characteristics is remembered and then used in

further calculations. The method is characterized by

the following features:

 A trajectory sequence is generated; each

trajectory is analyzed, which provides

information about the DMP taken control;

 Based on the analysis of so far generated

whole trajectories, it is possible to modify

coefficients used in local optimization or

change the form of local optimization

criterion when generating a new trajectory;

 In the course of trajectory creation,

the subsequent state of the process is being

analyzed and it is possible to modify the form

or/and parameters used in local optimization.

4 SCHEDULING PROBLEM

WITH STATE DEPENDED

RETOOLING

To illustrate the application of the presented method,

let us consider the following real life scheduling

problem that takes place during scheduling

preparatory works in mines. The set of headings in

the mine must be driven in order to render the

exploitation field accessible. The headings form a

net formally, represented by a nonoriented

multigraph G=(W,C,P) where the set of branches C

and the set of nodes W represent the set of headings

and the set of heading crossings respectively, and

relation P



(W×C×W) determines connections

between the headings (a partial order between the

headings).

There are two kinds of driving machines that

differ in efficiency, cost of driving and necessity of

transport. Machines of the first kind (set M1) are

more effective but the cost of driving by means of

them is much higher than for the second kind (set

M2). Additionally, the first kind of machines must

be transported when driving starts from another

heading crossing than the one in which the machine

is, while the second type of machines need no

transport. Driving a heading cannot be interrupted

before its completion and can be done only by one

machine at a time.

There are given due dates for some of

the headings. They result from the formerly prepared

plan of field exploitation. One must determine

the order of heading driving and the machine by

means of which each heading should be driven so

that the total cost of driving is minimal and each

heading complete before its due date.

There are given: lengths of the headings dl(c),

efficiency of both kinds of machines V

Dr(m)

(driving

length per time unit), cost of a length unit driven for

both kinds of machines, cost of the time unit waiting

for both kinds of machines, speed of machine

transport V

Tr(m)

and transport cost per a length unit.

The problem is NP-hard (Kucharska, 2006).

NP-hardness of the problem justifies the application

of approximate (heuristic) algorithms. A role of

a machine transport corresponds to retooling during

a manufacturing process, but the time needed for

a transport of a machine depends on the process state

while retooling does not.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

4.1 Formal Model of Problem

The process state at any instant t is defined as

a vector x=(x

,...,x

|M|

), where M=M1



M2.

A coordinate x

describes a set of heading (branch)

that has been driven to the moment t. The other

coordinates x

describes state of the m-th machine,

where m=1,2,...,|M|.

A structure of the machine state is as follows:

=(p,





)

(2)

where:

 p





{0} - represents the number of

the heading assigned to the m-th machine to

drive for p



C or no assignment for

the machine for p=0 (if the machine is not

assigned to a heading, i.e. the machine

remains idle at the crossing w);





W - the number of the crossing (node),

where the machine is located (if it is not

assigned to any heading, i.e. p=0) or

the number of the node, in which it finishes

driving the assigned heading c (information

about movement direction of the machine);





[0,∞) - the length of the route that remains to

reach the node



=w by the m-th machine,

whilst



=0 means, that the machine is in node



(0,dl(c)) means that the machine is

driving a heading, and the value of



is the

length that remains for the given heading c to

be finished, whilst



>dl(c) means that the

machine is being transported to the heading,

the value



is the sum of the length of heading

c and the length of the route until the

transportation is finished.

A state s=(x,t) belongs to the set of

non-admissible states if there is a heading whose

driving is not complete yet and its due date is earlier

than t. The definition S

is as follows:

={s=(x,t): (





C, c



)



d(c) < t}

(3)

where d(c) denotes the due date for the heading c.

A state s=(x,t) is a goal if all the headings have

been driven. The definition of the set of goal states

is as follows:

={s=(x,t) : s





(





C, c



)}

(4)

A decision determines the headings that should

be started at the moment t, machines which drive,

machines that should be transported, headings along

which machines are to be transported and machines

that should wait. Thus, the decision u=(u

,...,u

|M|

)

where the co-ordinate u

refers to the m-th machine

and u



{0}. u

=0 denotes continuation of

the previous machine operations (continuation of

driving with possible transport or further stopover).

=c denotes the number of heading c that is

assigned to be driven by machine m. As a result of

this decision, the machine starts driving the heading

c or is transported from the current location to

the node of the heading c, to which

the transportation route defined in the state s is

the shortest. This route is computed by the Ford’s

algorithm (a polynomial one).

Obviously, not all decisions can be taken in

the state (x,t). The decision u(x,t) must belong to

the set of possible (reasonable) decisions Up(x,t).

For example, a decision u

=c is possible only when

the c-th heading is neither being driven nor complete

and is available, i.e. there is a way to transport

machine to the one of the heading crossing adjacent

to the c-th heading or machine is standing in the one

of the heading crossings adjacent to the c-th heading.

Moreover, in the given state s=(x,t), to each

machine waiting in the node w, (it has not assigned

a heading to perform), we can assign an available

heading or it can be decided that it should continue

to wait. However, each machine which has been

previously assigned a heading and is currently

driving it or it is being transported to that heading,

can be only assigned to continue the current activity.

Also, none of the headings can be assigned to more

than one machine. The complete definition of the set

of the possible decision U

(x,t) will be omitted here

because it is not necessary to explain the idea of

the learning method.

Based on the current state s=(x,t) and

the decision u taken in this state, the subsequent

state (x’,t’)=f(u,x,t) is generated by means of

the transition function f. The transition function is

defined for each possible decision u(s)



(s).

Firstly, it is necessary to determine the moment

t’ when the subsequent state occurs, that is

the nearest moment in which at least one machine

will finish driving a heading. For that purpose, t

time of completion of the realized task needs to be

calculated for each machine. The subsequent state

will occur in the moment t’=t+



t, where



t equals

the lowest value of the established set of t

Once the moment t’ is known, it is possible to

determine the proper state of the process at the time.

The first coordinate x

of the proper state, that is the

set of completed headings, is increased by

OPTIMIZATION LEARNING METHOD FOR DISCRETE PROCESS CONTROL

Table 1: Particular parameters of the coordinate of the new machine state.

for the decision to continue the activity of the machine u

= 0:













ttfor

ttforp



’=



 



















































10,

0),(max

max,

0),(max

min

)(

MmfortV

Mmfor

cdl

tVt

cdl

mDr

mTr

mDr

mTr







for the decision to assign a new task to the machine u

= c:













ttfor

ttforc



’ =w

(c)













































2)(

10,

),(

max,

),(

min)(),(

)(

min

)(

min

)(min

MmfortVcdl

Mmfor

cmr

tVt

cmr

Vcdlcmr

mDr

mTr

mDr

mTr



the number of headings whose driving has been

finished in the moment t’.

Afterwards, the values of subsequent coordinates

in the new state are determined x’

=(p’,



’,



’), for

m=1,2...|M|, which represent the states of particular

machines.

Particular parameters of the coordinate of

the new machine state are determined in the way

described in Table 1, where w

adjacent to the heading c, in which the machine will

finish driving, and |r

min

(m,c)| is the length of the

shortest transportation route to the heading c for the

machine m.

4.2 Learning Algorithm

The algorithm based on the learning method consists

in generating consecutive trajectories. Each of them

is generated with the use of the specially designed

local optimization task and then is analyzed.

The information gained as a result of the analysis is

used in order to modify the local optimization task

for the next trajectory, i.e. for the next simulation

experiment. This approach is treated as a learning

without a teacher.

In the course of trajectory generation in each

state of the process, a decision is taken for which

the value of the local criterion is the lowest.

The local criterion takes into account a component

connected with cost of work, a component

connected with necessity for trajectory to omit

the states of set S

and a component for preferring

some decisions.

The first components is a sum of

Q(u,x,t) and

ˆQ(u,x,t) where

Q(u,x,t) denotes the increase of

work cost as a result of realizing decision u and

ˆQ(u,x,t) the estimate of the cost of finishing the set

of headings matching the final section of

the trajectory after the decision u has been realized.

The second component



(u,x,t)=E(u,x,t),

connected with the necessity for the trajectory to

omit the states of set S

, is defined by means of

a semimetrics.

The third component is aimed at reduction of

machine idleness time. Since the model considers

the possibility that the machines will stand idle in

certain cases, it seems purposeful to prefer decisions

which will engage all machines to for most of

the time. It is therefore necessary to reduce

the probability of selecting the decision about

machine stopover when headings are available for

driving and machines could be used for work. This

may be realized by using an additional auxiliary

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

criterion



(u,x,t)=F(u,x,t), which takes into

consideration penalty for a decision about a stopover

in the case of a machine which could have started

work.

Thus, the local criterion is of the form:

q(u,x,t)=



Q(u,x,t)+̂Q(u,x,t)+



E(u,x,t)+b



F(u,x,t)

(5)

where

, b

are weights of particular

components.

In the course of trajectory generation, the local

optimization task may be changed. Problem

analysis reveals that the moment all headings with

due dates are already finished, it is advisable to use

only cheaper machines. Formally, this corresponds

to the limitation of the set of possible decisions

Up(s).

Moreover, it is no longer necessary to apply

the

component

E(u,x,t)

in the local criterion.

The modified form of the criterion can be then

represented as follows:

q(u,x,t)=



Q(u,x,t)+̂Q(u,x,t)+ b



F(u,x,t)

(6)

In order to select a decision in the given state s, it

is necessary to generate and verify the entire set of

possible decisions in the considered state U

(s). For

each decision u

, it is necessary to determine

the state the system would reach after realizing it.

Such a potentially consecutive state of the process

will be represented as s

p_k

=(x

p_k

Afterwards, the criterion components are

calculated. The increase of cost



Q(u

,x,t) is the sum

of costs resulting from the activities of particular

machines in the period of time t

p_k

-t. The estimate of

the cost of the final trajectory section ˆQ(u

,x,t) can

be determined in a number of ways. One of these is

to establish the summary cost of finishing previously

undertaken decisions, whose realization has not been

completed yet, and the cost of a certain relaxed task,

realized in the cheapest way. Taking into

consideration that the estimate should take place

with the lowest number of calculations, relaxation

has been proposed which would include omitting

temporal limitations and the assuming the least

expensive procedure for finishing the remaining

headings; this would involve using the least

expensive machines.

The component of the local criterion E(u

,x,t)

uses the value of the estimated “distance” between

the state s

p_k

, and the set of inadmissible states.

The distance is estimated with the help of

semimetrics



(s,S

)=min{



(s,s’): s’



Assuming that the speed of transporting

the “fastest” machine is significantly higher than its

speed of performance, and this one in turn

significantly exceeds the speed of performance of

the remaining machines, it is possible to omit

the time of transporting the fastest machine. For

the sake of simplicity, let us assume that there is one

fastest machine.

One of the methods of determining

the component E(u

,x,t) is to calculate, for each not

realized and not assigned heading c with due date,

the time reserve rt

p_k

Taking into consideration these assumptions,

the time reserve is defined by the following formula:

)=d(c)-t



(c)-t

end

(7)

where:

 d(c) - due date for the heading c;





the headings situated along the shortest route

from the heading c to the so-called realized

area in the given state, by the fastest machine;

 t

end

- time necessary to finalize the current

activity of the fastest machine

The parameters t

end

and



situations:

a) “the fastest” machine may continue

the previously assigned task to drive another

heading.

b) heading c may be inaccessible and it might

be necessary to drive the shortest route to this spot

from the realized area, involving already excavated

headings as well as those assigned for excavation

together with relevant crossings. For the period of

time when the fastest machine finishes

the excavation of the previously assigned heading,

a fragment of this distance may be excavated by the

fastest of the remaining machines. When the heading

is accessible the time equals to the time of

excavating the length of the heading with the fastest

machine.

Finally, the component estimating the influence

of time limitations assumes the following form:

min ( ) 0

(,,)

min ( ) 0

min ( )

cpk

for rt s

Eu xt

for rt s

rt s



















(8)

As a result, the decision to be taken, from the set

of considered decisions, is the one for which the

subsequent state is most distant from the set of

non-admissible states.

The shape of the local criterion component

F(u

,x,t) in certain cases should make it purposeful

to prefer decisions which will engage all machines

OPTIMIZATION LEARNING METHOD FOR DISCRETE PROCESS CONTROL

for most of the time. It is therefore necessary to

reduce the probability of selecting the decision about

machine stopover when headings are available for

driving and machines could be used for work. For

that purpose, a penalty may be imposed for the

stopover of each machine that could potentially start

driving an available heading. The proposed form of

F(u

,x,t) is the following:

F(u

,x,t)=P



waitin

(9)

where:

 P - denotes the penalty for machine stopover,

(calculated for the decision about stopover

when there are still headings available for

work);

 i

waiting

- the number of machines that are

supposed to remain idle as a result of such

a decision.

The values a

and b

are respectively coefficients

defining the weight of particular components of

the local criterion q(u,x,t) and reflect current

knowledge about controls, whilst their values change

in the course of calculations. The higher the weight

of a given parameter, the higher its value.

The weights depend both on the considered

optimization problem as well as input data for

the particular optimization task (instance).

Coefficient values, as well as their mutual

proportions are not known nor can they be

calculated a priori.

The knowledge gained in the course of

experiments may be used to change weight values. If

the generated trajectory is non-admissible, then for

the subsequent trajectory, the value of weight a

should be increased; which means the increase of

the weight of the component estimating the distance

from the set of non-admissible states and/or

the increase of weight b

value, which would result

in lower probability of machine stopover.

Whereas, if the generated trajectory is

admissible, then for the subsequent trajectory the

values of this coefficients may be decreased.

4.3 Experiments

The aim of conducted experiments was to verify the

effectiveness of applying the components E(u,x,t)

and F(u,x,t) in the local criterion.

The research was conducted for the set of 10

heading networks. Each network is represented by

a planar graph, in which the vertex degrees equal

from 1 to 4. The lengths of headings are numbers

from the range [19, 120]. The number of headings

with due dates is approximately 25% of all headings.

The parameters of heading networks used in

simulation experiments are given in Table 2.

Also, two examples of network are presented in

Figure 1.

Two machines are used to perform the task

during our experiments, one of the first type and one

of the second type. Parameters for both types of

machines are given in the Table 3.

The effectiveness of component E(u,x,t) for each

network was tested by constructing 40 trajectories

with the changing value of coefficient a

and zero

value of coefficient b

Table 2: The heading network parameters.

Parameter GI-1a GI-1b GI-2

GI-3 GII-4 GII-5a GII-5b GII-6 GII-7 GII-8

Number of heading

20 20 20

20 24 27 27 29 67 68

Number of heading crossing

18 18 18

18 20 20 20 20 50 50

Length of the shortest

heading

20 20 22

19 30 30 30 30 30 30

Length of the longest

heading

109 109 106

120 81.59 107.52 107.52 94.75 114.65 111.95

Sum of the length of

the headings

1008 1008 1010 1066 1364.45 1863.07 1863.07 1869.88 4579.11 4607.81

Number of heading with

deadline

5 5 5

5 5 5 5 5 18 16

Minimum deadline

55 60 55

55 60 70 100 50 80 80

Maximum deadline

70 60 70

70 100 150 100 100 320 200

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

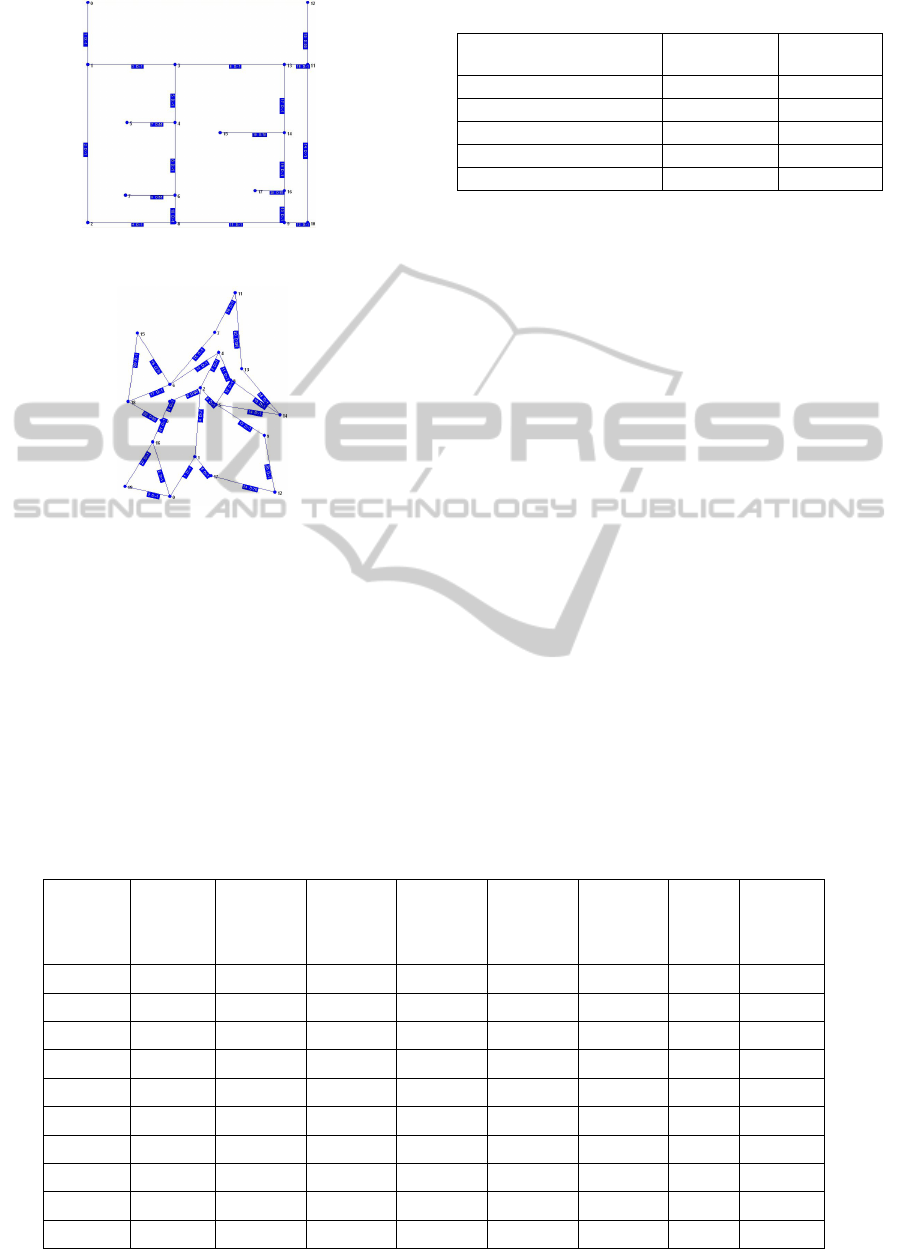
Figure 1a: Example of heading network - GI-1a.

Figure 1b: Example of heading network - GII-5.

Table 4 presents results for one of the tested

networks, i.e. for network GII-4.

The time reserve refers to the time that remains after

a given heading has been driven until the due date,

whilst the minus value means that the due date has

been exceeded. The symbol ”*” means that heading

driving has not commenced because the trajectory

reached a non-admissible state. Based on

the obtained results, it can be concluded that

increasing the value of E(u,x,t) increases

the probability of obtaining an admissible solution.

Table 3: Parameters of the machines.

Parameter Machine of

M1 type

Machine

of M2 type

Efficiency [m/h]

10.0 5.0

Transport speed [m/h]

100.0 unspecified

Driving cost [$/h]

200.0 50.0

Transport cost [$/h]

100.0 0.0

Waiting cost [$/h]

30.0 5.0

When the component E(u,x,t) was omitted,

an admissible solution was not found.

Table 5 presents in columns the best obtained

total cost at changeable value of coefficient b

responsible for the weight of component F(u,x,t) in

the local criterion. In most cases, the increase of

weight of this component resulted in increased total

costs, but at the same time the probability of finding

an admissible solution was higher. Moreover, in

some cases, the use of this component resulted in

decreased total costs of performing work. A lot of

this experiments have been conducted, they are

presented in (Kucharska, 2006). Unfortunately, they

must be omitted here because the limited length of

the paper.

The experiments have confirmed effectiveness

of the use of the component F(u,x,t).

To evaluate the effectiveness of the proposed

algorithm one has compared the obtained results

with the optimal solution. A complete review

algorithm for all considered heading network has

been applied. To reduce calculations, the generation

of each trajectory was interrupted when the lower

estimate of its cost in a given state was greater than

the best found solution.

Table 4: The effectiveness of applying parameter E(u,x,t) for the network GII-4.

Coeff. a

Total

cost

Time

reserve of

head. 4

Time

reserve of

head. 9

Time

reserve of

head. 12

Time

reserve of

head. 16

Time

reserve of

head. 22

Min.

reserve

Average

reserve

0 - 7.40 * * * * - -

1 - 12.90 * * * * - -

50 - 12.90 * -0.62 * * - -

5000 - 12.90 * -2.84 * * - -

7500 22887.64 12.90 4.02 7.68 5.15 11.64 4.02 8.28

25000 23153.10 13.18 32.10 48.01 1.46 2.67 1.46 19.48

50000 23359.93 12.90 21.73 48.01 38.90 30.34 12.90 30.38

75000 23204.35 25.18 19.42 48.01 20.54 25.59 19.42 27.75

500000 23027.78 27.47 20.13 19.71 40.06 29.18 19.71 27.31

2500000 23084.25 27.47 20.13 19.71 36.57 37.53 19.71 28.28

OPTIMIZATION LEARNING METHOD FOR DISCRETE PROCESS CONTROL

Table 5: Effectiveness of applying component F(u,x,t).

Network

Best found cost

=0 b

=0,5 b

=1 b

=2 b

GI-1a 17026.90 17026.90 17249.10 16922.00 16922.00

GI-2 * * * 17284.10 17284.10

GI-3 16359.90 16359.90 16359.90 16359.90 16359.90

GII-4 22665.17 22665.17 22667.89 22667.89 22667.89

GII-5a 30982.02 30946.33 31004.27 31004.27 31004.27

GII-5b 30888.34 30888.34 31139.72 31139.72 31139.72

GII-6 30662.32 30675.19 30675.19 30675.19 30675.19

GII-7 77428.92 77717.02 77288.44 77717.02 77717.02

Table 7: Comparison of results from the solution obtained by a complete review of the algorithm for which the calculations

were interrupted.

Network

Review algorithm

Best cost founded by

learning algorithm

Percentage

difference of cost

time to stop

calculation

best found cost

GI-1a 43h 48min 16480,00 16922.00 2,68%

GI-3 43h 41min 17448,90 16359.90 -6,24%

GII-4 44h 3min 23132,40 22665.17 -2,01%

GII-6 43h 38min 31142,54 30662.32 -1,54%

The lower bound was calculated as the sum of

the cost of the current part of trajectory and a cost

estimation of remaining part.

Optimal solution was found only for network

GI-2. In other cases, the calculations were

interrupted after more than 2 days. Only for four

networks an admissible solution has been found,

while for the other networks an acceptable solution

has not been found during 2 days.

The comparison between the optimal cost with

the best found cost is presented in Table 6. Error of

found solution is also given. It can be noticed that

the proposed learning algorithm has found very good

solution (almost optimal). It should be point out also

that the its calculation time was very short (a several

seconds). While the exact algorithm needs very long

time (over 40 hours).

Table 6: Comparison of results from the optimal solution.

Net-

work

Time for the

optimal

solution

Optimal

cost

The best

cost

found by

the

proposed

algorithm

Error of

found

solution

GI-2 43h 43min 59s 16524.40 17284.10 4.59%

The comparison of the learning algorithm results

with solution obtained by complete review algorithm

after over 40 hour are presented in Table 7. Also,

the time after which the calculation of the algorithm

was stopped, and the cost of which could be

determined at this time are given. Percentage

difference of cost is calculated as

(LAcost-RAcost)/RAcost where LA, RA denote best

cost calculated by learning algorithm and completed

review algorithm respectively.

The result of experiments shows that

the difference between sub-optimal cost and the best

found by the learning algorithm is small and in

the worst case is 4.59%. One can say that

the learning algorithm finds a better solution in most

cases.

Based on the obtained results, it can be

concluded that the application of the proposed

algorithm for the DMP problem yields very positive

results.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

5 CONCLUSIONS

The paper presents a conception of intelligent search

method for optimization of discrete manufacturing

processes control (scheduling, planning).

The method uses a sophisticated structure of local

optimization task. The structure as well as

parameters of the task are modified during search

process. It is done on a basis of gathering

information during previous iterations. Thus

the method is a learning one. The method is based

on a general formal model of discrete manufacturing

processes (DMP), that is given in the paper.

A large number of difficult scheduling problems

in manufacturing can be efficiently solved by means

of the method. Moreover, the proposed method is

very useful for another difficult scheduling

problems, especially for problems with state

depended resources. Managing projects, especially

software projects belongs to this class.

To illustrate the conception, some NP-hard

problem, namely a scheduling problem with state

depended retooling is considered and the learning

algorithm for it is presented. Results of computer

experiments confirm the efficiency of the algorithm.

REFERENCES

Dudek-Dyduch, E., 1990. Formalization and Analysis of

Problems of Discrete Manufacturing Processes.

Scientific bulletin of AGH Academy of Science and

Tech., Automatics vol.54, (in Polish).

Dudek-Dyduch E., 1992. Control of discrete event

processes - branch and bound method. Proc. of

IFAC/Ifors/Imacs Symposium Large Scale Systems:

Theory and Applications, Chinese Association of

Automation, vol.2, 573-578.

Dudek-Dyduch, E., 2000. Learning based algorithm in

scheduling. In Journal of Intelligent Manufacturing.

vol.11, no 2, 135–143.

Dudek-Dyduch, E., Dyduch, T., 1988. Scheduling some

class of discrete processes. In Proc. of 12th IMACS

World Congress, Paris.

Dudek-Dyduch, E., Dyduch, T., 1993. Formal approach to

optimization of discrete manufacturing processes. In

Hamza M.H. (ed), Proc. of the Twelfth IASTED Int.

Conference Modelling, Identification and Control,

Acta Press Zurich.

Dudek-Dyduch, E., Dyduch, T., 2006. Learning

algorithms for scheduling using knowledge based

model. In Rutkowski L.., Tadeusiewicz R. Zadech L.A.,

Żurada J.(ed) Artificial Intelligence and Soft

Computing , Lecture Notes in Artificial Intelligence

4029. Springer.

Dudek-Dyduch, E., Fuchs-Seliger, S., 1993. Approximate

algorithms for some tasks in management and

economy. In System, Modelling, Control. no 7, vol.1.

Johnsonbaugh R., Schaefer M., 2004. Algorithms. Pearson

Education International.

Kolish, R., Drexel, A., 1995. Adaptive Search for Solving

Hard Project Scheduling Problems. Naval Research

Logistics, vol.42.

Kucharska, E., 2006. Application of an algebraic-logical

model for optimization of scheduling problems with

retooling time depending on system state. PhD thesis

(in polish).

Pearl, J., 1988. Heuristics : Intelligent search strategies

for computer problem solving. Addison-Wesley

Comp. Menlo Park.

Rajedran, C., 1994. A no wait flow shop scheduling

heuristic to minimize makespan. In Journal of

Operational Research Society 45. 472–478.

Sprecher, A., Kolish, R., Drexel, A., 1993. Semiactive,

active and not delay schedules for the resource

constrained project scheduling problem. In European

Journal of Operational Research 80. 94–102.

Vincke, P., 1992. Multicriteria decision-aid. John Wiley

& Sons.

OPTIMIZATION LEARNING METHOD FOR DISCRETE PROCESS CONTROL