
ON THE DETECTION OF BINARY
CONCENTRATION-ENCODED UNICAST
MOLECULAR COMMUNICATION IN NANONETWORKS
Mohammad Upal Mahfuz, Dimitrios Makrakis and Hussein Mouftah
School of Information Technology and Engineering, University of Ottawa, K1N6N5 Ontario, Canada
Keywords: Molecular communication, Concentration encoding, Sampling-based detection, Energy-based detection,
Nanonetworks.
Abstract: Molecular communication is a new communication technique where transmitter and receiver communicate
by transmitting molecules and correspondingly modulating their specific characteristics. Molecular
communication is being considered as a new physical layer (PHY) option for a vast number of
communicating nanomachines that form “nanonetworks.” Thus it has become a promising option for a large
number of new applications, offering several benefits over conventional electromagnetic communications
based on radio waves or optics at nanoscale dimension. Concentration-encoding is a simple and good
technique to encode information with molecules. Incorrect detection of concentration-encoded signals
makes molecular communication a real challenge. This paper has addressed sampling-based and energy-
based detection approaches in detail for binary concentration-encoded molecular communication signals
based on diffusion in fluidic media.
1 INTRODUCTION
Molecular communication is a new physical layer
option that is being considered for communication
and networking among a huge number of natural and
man-made nanomachines (Akyildiz et al. 2008,
Mahfuz et al. 2010a, Mahfuz et al. 2010b). A
nanomachine is a tiny machine capable of
performing simple tasks e.g. sensing and actuation.
As shown in Fig.1 a transmitting nanomachine (TN)
transmits molecules in a fluidic medium, the
molecules propagate in the medium following the
diffusion process, and then finally the molecules are
received by the receiving nanomachine (RN).
Detection of concentration-encoded molecular
signals is very crucial in the sense that incorrect
detection of concentration-encoded signals would
result in wrong decoded bit, thus producing bit
errors, and finally the effect / reaction performed by
the RN would be erroneous. In this paper we have
explained two detection approaches, named
“sampling-based detection (SD)” and “energy-based
detection (ED),” for binary concentration-encoded
molecular communication in order to detect the
information bits transmitted by TN and that are
available at the location of RN in the form of
received throughput of the molecular propagation
channel. We have also shown threshold
characteristics for “known-reference” and “blind-
reference” cases for bit detection. In the former case,
RN knows the average transmission rate used by TN
(in molecules/second) beforehand, and thus RN can
compute the threshold concentration as a function of
known transmission rate for a given distance
between TN and RN. On the other hand, in blind-
reference case RN does not know the transmission
rate of molecules beforehand, and so RN computes
the threshold concentration as a function of available
throughput at its own location. Although threshold
computation is an important aspect for molecular
communication, it has not been addressed in depth
so far in open literature. The paper is organized as
follows: section-2 briefly discusses the throughput
of the channel, followed by section-3 discussing the
fundamental concepts of sampling-based (SD) and
energy-based (ED) detection methods for the
amplitude modulated concentration-encoded signal.
Finally, section-4 concludes the paper.
446
Upal Mahfuz M., Makrakis D. and Mouftah H..
ON THE DETECTION OF BINARY CONCENTRATION-ENCODED UNICAST MOLECULAR COMMUNICATION IN NANONETWORKS.
DOI: 10.5220/0003158504460449
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 446-449
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
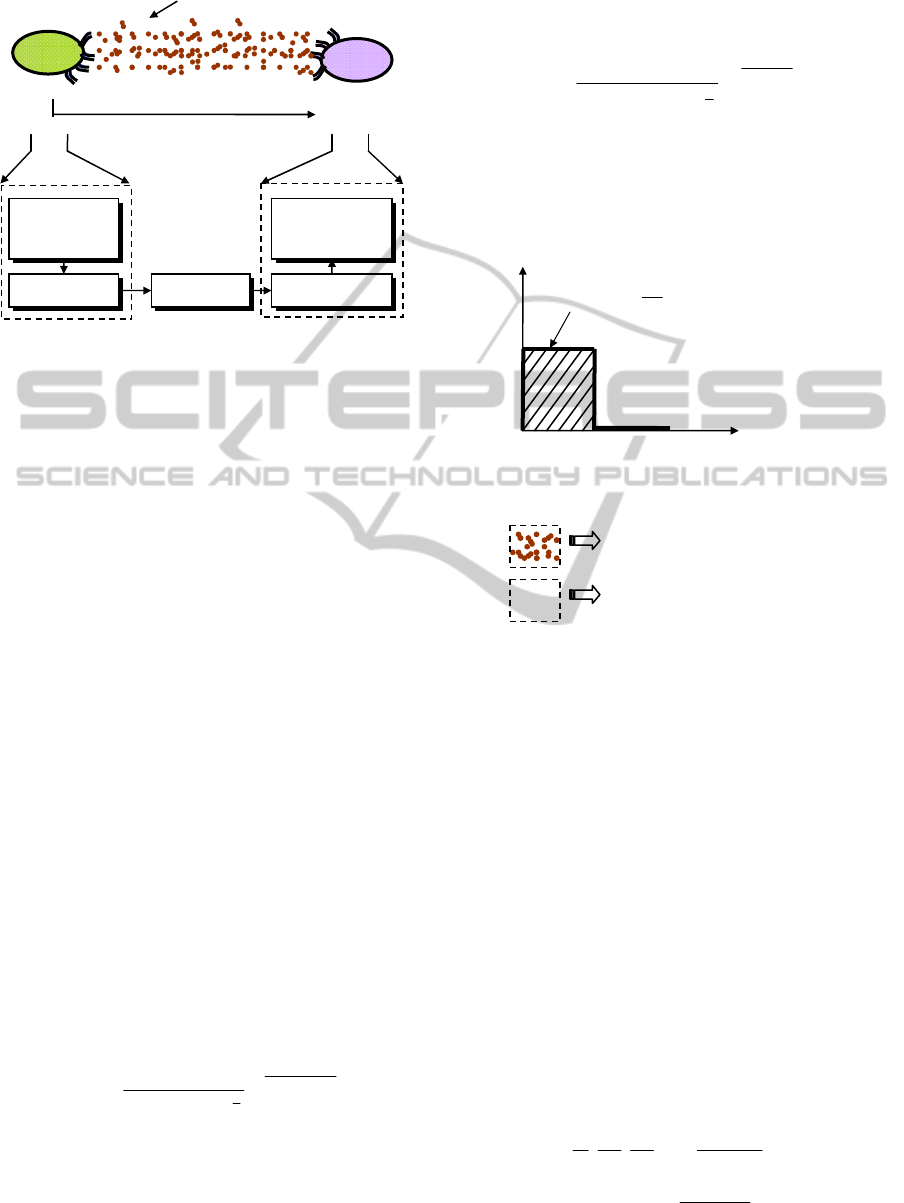
Figure 1: A generic molecular communication channel
between a transmitting nanomachine (TN) and a receiving
nanomachine (RN).
2 PROPAGATION OF
MOLECULES
We have assumed binary amplitude modulation for
the concentration-encoded signal. We assume that
TN is a nanomachine or a biological entity that can
emit only one kind of molecule. We consider
hypothesis H
1
as the case when bit ‘1’ is to be
transmitted, and hypothesis H
0
as the case when bit
‘0’ is to be transmitted. Correspondingly, TN
transmits
average
Q molecules per second on an average
for the entire bit duration of
T
b
seconds for H
1
, while
TN does not transmit any molecules at all for
H
0
. As
shown in Fig.2, transmission stimulation protocol
can be expressed as
1
0
;
()
0;
average
QH
Qt
H
⎧
=
⎨
⎩
(1)
Assuming a point source type TN the concentration
of molecules
(,)Urtin molecules per unit volume
at a three-dimensional space
ˆ
ˆˆ
rixjykz=⋅+⋅ +⋅
G
and
at time
t changes with time and space as the well-
known Roberts equation (Bossert and
Wilson 1963)
as shown below
()
{}
()
()
222
4
3
0
2
()
,,,
4( )
xyz
t
Dt
Q
Uxyzt e d
Dt
τ
τ
τ
πτ
−++
−
=⋅
−
∫
(2)
where
r
G
is the distance vector between TN and RN,
τ
is a dummy variable of integration, and D is the
diffusion constant of information molecules in the
medium in cm
2
/second unit. Considering spherical
symmetry Eq.(2) can be written as a function of
r (in
cm)
as (Berg 1993).
()
()
{}
()
2
4
3
0
2
()
,
4
r
t
Dt
Q
Urt e d
Dt
τ
τ
τ
πτ
−
−
=⋅
−
∫
(3)
where
r
2
=x
2
+y
2
+z
2
when a Cartesian coordinate
system is assumed. In a simple manner
U(r,t) is also
known as the throughput of the molecular
propagation channel.
Figure 2: Binary concentration-encoded molecular
signalling, Q
0
representing the total number of molecules
transmitted by TN during T
b
.
3 DETECTION APPROACHES
3.1 Sampling-based Detection (SD)
As shown in Fig.3 with SD approach the propagation
channel is excited with a random bit sequence of
N
bits transmitted by the TN, and correspondingly the
throughput
U(r,t) is sampled at any suitable time
instant during the bit duration
T
b
. However, with the
assumption that TN is in time-synchronization with
RN we assume that the sampling instants are at
exactly the middle of any bit duration and thus can be
expressed as
Samples
35 (21)
, , ,......., ,...
22 2 2
(2 1)
...,
2
bbb b
b
TTT n T
NT
t
−
−
=
(4)
t (seconds)
Q(t)
(0,0)
0
average
b
Q
Q
T
=
T
b
2T
b
(b) Binary modulation of transmission rate
Bit ‘1’
(Q
average
molecules/second)
Bit ‘0’
(No transmission of molecules)
(a) Input stimulation protocol
TN
RN
Information
molecules
Molecular propagation channel
Information
Source
Modulator
Reaction
or Effect
Demodulator Channel
U( r
G
,t)
r=0,
t=0
ON THE DETECTION OF BINARY CONCENTRATION-ENCODED UNICAST MOLECULAR COMMUNICATION
IN NANONETWORKS
447
where N is the total number of bits in the bit
sequence,
T
b
is the duration of each bit, and
1, 2,3,...,nN=
is the index of bits. As a result, the
detection variable or test statistic (Kay 1998)
SD
Z
for
detecting the
n
th
bit is denoted as
(2 1)
2
,.
b
SD
nT
ZUr
−
⎡⎤
=
⎢⎥
⎣⎦
(5)
For a given data rate f, bit duration is fixed at T
b
=1/f.
However, since throughput U(r,t) received at the
location of RN largely depends on the distance r
(Mahfuz et al. 2010b),
SD
Z
is a function of both
distance r and diffusion constant D. For all practical
reasons assuming D to remain constant over the
entire observation period T, we find that
SD
Z
becomes significantly affected by r. For known-
reference SD approach, RN has prior knowledge of
the transmission rate of input (i.e. Q(t)=Q
average
), and
thus the most common threshold can be given as
Known
SD
2
average
Q
K =
(6)
Figure 3: Sampling based (SD) detection for transmitted
bits {101100}. Sampling instants are shown in red arrows,
L
g
denoting the level gap between maximum and
minimum points of U(r,t) when a bit toggles.
Since
SD
Z
is significantly affected by r, known-
reference SD approach should be used in short-range
molecular communication (Mahfuz et al. 2010b).
Threshold for blind reference case is given below as
the average throughput
U(r,t) over the interval from 0
to 2
T
b
seconds as shown in transmission protocol in
Fig.2,
{}
Blind
SD
over time duration 0 to 2
Average ( , )
b
T
KUrt=
(7)
However,
Blind
SD
K is highly influenced by r as shown in
Fig.4 below.
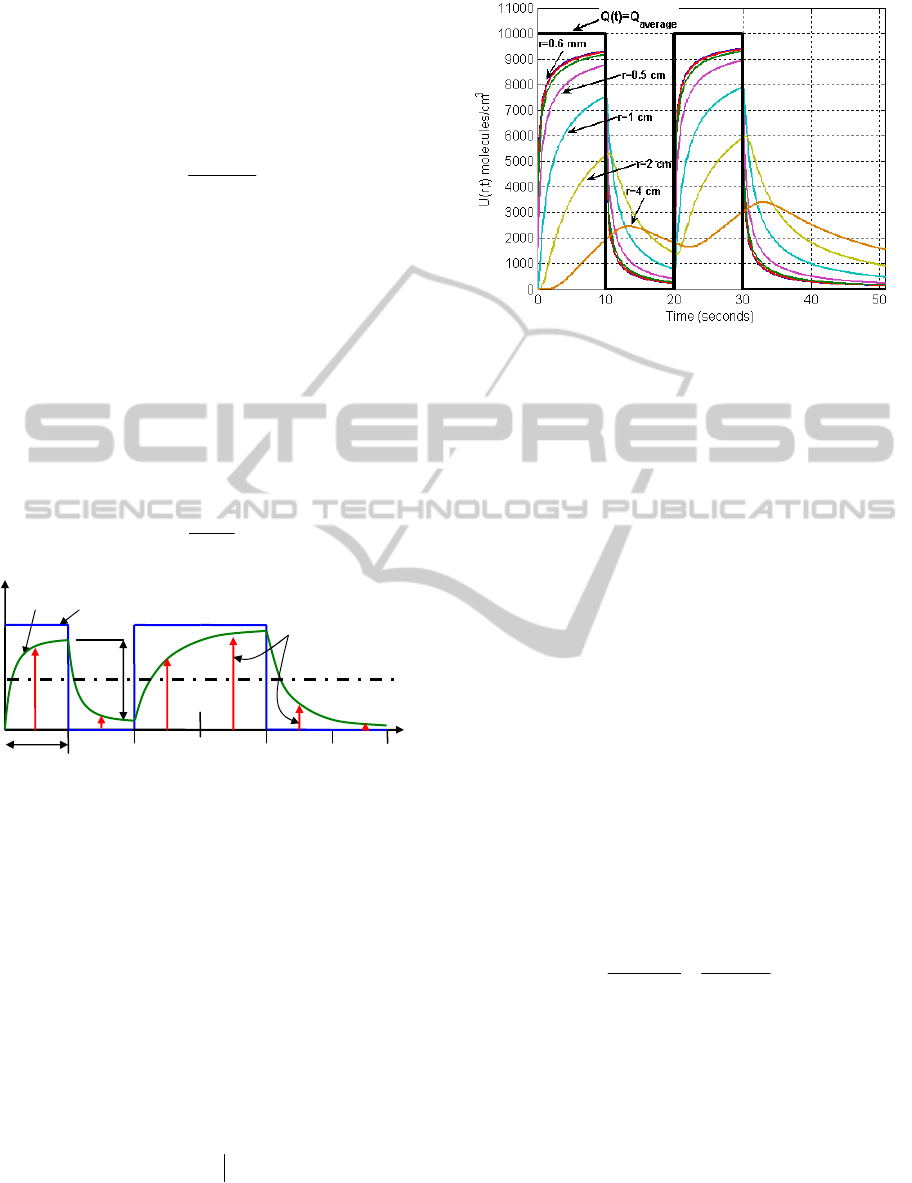
Figure 4: Distance dependence of throughput, with
Q
average
=10,000 molecules/sec., T
b
=10 seconds, random bit
sequence {10100} in air medium.
3.2 Energy-based Detection (ED)
As shown in Fig.5 with ED approach available
throughput U(r,t) in molecules per unit volume is
integrated over any entire bit duration T
b
seconds and
the resulting accumulated amount of molecules is
termed as the detection variable
ED
Z
for the
corresponding bit and expressed as
() ( )
(1)
,
b
b
nT
ED
nT
Z
nUrtdt
−
=
∫
(8)
where
1, 2,3,...,nN
=
is the index of the bit and N is
the total number of bits in the random bit sequence.
Referring to Fig.2, in known-reference ED approach
RN detects a bit when the accumulated molecules
during T
b
is greater than or equal to the threshold
Known
ED
K that is most commonly the half of the total
transmitted energy during 0 to 2T
b
seconds as shown
below
2
Known
0
ED
()
22
b
T
average b
Qtdt
QT
K ==
∫
(9)
The threshold given by Eq.(9) is independent of r,
however, as shown in Fig.4 the throughput U(r,t) is
highly influenced by the variation of distance r. As a
result, this distance-dependence of throughput makes
the threshold selection inappropriate for known-
reference ED approach. On the other hand, in blind-
reference ED approach RN does not know the
transmission rate of TN. As a result, RN can compute
the threshold as the average integral of throughput
for the duration from 0 to 2T
b
as shown in Fig.2.
t (sec.)
U(r,t)
Q(t)=Q
average
T
b
L
g
Samplin
g
Bit
‘1’
Bit
‘0’
Bit
‘1’
Bit
‘1’
Bit
‘0’
Bit
‘0’
2T
b
… nT
b
Threshol
d
3T
b
0
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
448

Thus the threshold for blind-reference case can be
expressed as
2
Blind
0
ED
(,)
2
b
T
Urtdt
K =
∫
(10)
as shown in the transmission protocol in Fig.2. As
shown in Fig.4 since throughput U(r,t) varies with
the varying distance, threshold in blind-reference
case should vary as per the variation of the distance
between TN and RN.
Figure 5: Concept of energy-based detection with a
random bit sequence {101100}.
4 CONCLUSIONS
In this paper detection methods for binary
concentration-encoded molecular communication
channel has been addressed. Sampling-based and
energy-based detection methods have been proposed
as possible detection schemes for concentration-
encoded signals. Three important factors that affect
the performance of detection methods are noise
immunity, distance-dependence of throughput, and
timing synchronization of TN and RN. The SD
approach detects the bit based on only one sample
value of the throughput taken at the sampling
instant. Thus SD approach is applicable for ideal
environment and for short ranges, and so it is not
recommended for most real cases where the
communication is impaired with noise and/or for
medium-to-long range communications. Since
throughput varies with varying distance a fixed
threshold for known-reference case tends to be a
strict selection, whereas for blind-reference case RN
has to compute the threshold from the throughput
only, making the threshold highly dependent on the
distance between TN and RN. Finally, timing
synchronization can be achieved by correctly
characterizing the propagation delay between TN
and RN. While a synchronizing clock for molecular
communication can be difficult, asynchronous
signalling (Moore et al. 2007) can also be used for
the purpose of detection of molecular signals.
ACKNOWLEDGEMENTS
The first author would like to thank the Natural
Sciences and Engineering Research Council of
Canada (NSERC) for the financial support in the
form of doctoral scholarship to carry out this
research work.
REFERENCES
Akyildiz, I. F., F. Brunetti, and C. Blazquez (2008)
“NanoNetworking: A New Communication
Paradigm,” Computer Networks, Vol. 52, pp. 2260-
2279, Elsevier, August.
Berg, H. C. (1993) Random Walks in Biology, Princeton
University Press.
Bossert, W. H., and E. O. Wilson (1963) “Analysis of
Olfactory Communication among Animals,” Journal
of Theoretical Biology, pp.443-469.
Kay, S. M. (1998) Fundamentals of Statistical Signal
Processing, Vol. 2: Detection Theory, Prentice Hall.
Mahfuz, M. U., D. Makrakis, and H. Mouftah (2010a)
“Characterization of Molecular Communication
Channel for Nanoscale Networks,” in Proc. 3
rd
International Joint Conference on Biomedical
Engineering Systems and Technologies (BIOSTEC
2010), Valencia, Spain, 20-23 January.
Mahfuz, M. U., D. Makrakis, and H. Mouftah (2010b)
“Spatiotemporal Distribution and Modulation
Schemes For Concentration-Encoded Medium-to-
Long Range Molecular Communication,” in Proc. 25
th
Biennial Symposium on Communications, Kingston,
ON, Canada, 10-12 May.
Moore, M., A. Enomoto, T. Suda, T. Nakano, and Y.
Okaie (2007) “Molecular Communication: New
Paradigm for Communication Among Nano-Scale
Biological Machines,” The Handbook of Computer
Networks, John Wiley & Sons Inc., November.
t (sec.)
Q(t)=Q
average
T
b
Bit
‘1’
Bit
‘0’
Bit
‘1’
Bit
‘1’
Bit
‘0’
Bit
‘0’
2T
b
… nT
b
Desired energy for the first Bit ‘1’
Interference energy from the first Bit ‘1’ to
the first Bit ‘0’
3T
b
U(r,t)
ON THE DETECTION OF BINARY CONCENTRATION-ENCODED UNICAST MOLECULAR COMMUNICATION
IN NANONETWORKS
449
