GENETIC ALGORITHM BASED ON DIFFERENTIAL

EVOLUTION WITH VARIABLE LENGTH

Runoff Prediction on an Artificial Basin

Ana Freire, Vanessa Aguiar-Pulido

Department of Comunications and Information Technologies, University of A Coruña

Campus Elviña s/n, A Coruña, Spain

Juan R. Rabuñal

Centre of Technological Innovation in Civil Engineering, University of A Coruña

Campus Elviña s/n, A Coruña, Spain

Marta Garrido

Water Engineering and Environmental Group, University of A Coruña

Campus Elviña s/n, A Coruña, Spain

Keywords: Differential evolution, Hydrology, Evolutionary computation.

Abstract: Differential evolution is a successful approach to solve optimization problems. The way it performs the

creation of the individual allows a spontaneous self-adaptability to the function. In this paper, a new method

based on the differential evolution paradigm has been developed. An innovative feature has been added: the

variable length of the genotype, so this approach can be applied to predict special time series. This approach

has been tested over rainfall data for real-time prediction of changing water levels on an artificial basin.

This way, a flood prediction system can be obtained.

1 INTRODUCTION

Differential evolution was firstly named in 1998 by

Kenneth Price and Rainer Storn (Storn and Price,

1997). This is a powerful evolutionary algorithm for

solving optimization problems over continuous

spaces. DE has been applied to several fields and its

good behaviour has become clear. The secret lies in

the way DE generates the population after each

generation (Storn and Price, 1997), (Feoktistov,

2006). This process uses three operators: mutation,

crossover and selection. The first two operators

generate the candidate vectors and the last one

decides which one enters the next generation.

1.1 Mutation

The population is initialized by a set of NP randomly

generated individuals (x

i,G

, i=1..NP). At each

generation, three mutually different individuals

(random vectors) are randomly chosen from the

population below (general mutation strategy). Then,

a mutant vector (v) is generated in the way written:



,



,

·

,



,

 (1)

i=1...NP

The parameter F (scaling factor) tries to manage

the trade-off between exploitation and exploration of

the search space.

Although only one mutation scheme was

presented here, there are several ways of

implementing this operator. Depending on the

problem, one strategy will be more suitable than

others. Some research works (Qin et al., 2009)

alternate different strategies and parameter values on

different generations depending on the cost function

value.

In (Feoktistov, 2006) several strategies are

divided in four groups:

1. RAND group: the trial individual is generated

207

Freire A., Aguiar-Pulido V., Rabuñal J. and Garrido M..

GENETIC ALGORITHM BASED ON DIFFERENTIAL EVOLUTION WITH VARIABLE LENGTH - Runoff Prediction on an Artiﬁcial Basin.

DOI: 10.5220/0003081402070212

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 207-212

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

without any information about the values of the

objective function.

2. RAND/DIR group: strategies that use values of

the objective function to determine the good

direction.

3. RAND/BEST group: the best individual is used

to form the trial one.

4. RAND/BEST/DIR group: combines the

advantages of the last two groups.

The strategy to choose is always defined by the

problem and the concrete objective function.

1.2 Crossover

Once the mutant vectors have been generated, the

crossover is performed in order to intensify the

search inside a region. This step is performed based

on the crossover constant (CR), which is given a

random value between 0 and 1. Then, the trial

vectors are generated as follows:



,





,1

,











,

,















j=1...D (2)

1. D represents the dimensionality of the problem.

2. randb(j) generates a random number between 0

and 1for the j component.

3. rnbr(i) generates a number between 1 and D

which ensures that u

i,G+1

gets at least one parameter

from 

i,G+1

1.3 Selection

Once these two operations have been performed, the

trial vector is compared to the target vector; if the

trial vector achieves a smaller cost function value, it

will be included in the next generation; otherwise,

the target vector will be kept.

The main idea of this approach is to adapt the

step length intrinsically along the evolutionary

process. As the evolution goes on, the population

converges and the step length becomes smaller.

2 MOTIVATION

Many problems need to calculate the parameters that

fit a function in order to establish a prediction based

on correlations. Therefore, a useful technique is to

consider a sliding window which includes some

prior values to the current one (t) in order to

calculate the next one (t+1). Time series prediction

is an example of this kind of problems.

If we want to apply the differential evolution

approach to this kind of problem, we must perform

an adaptation of the basic algorithm.

Therefore, this paper proposes a differential

evolution approach where the individuals can have

different lengths. On one hand, the length of the best

individual offers the size of the time window; on the

other hand, each gene corresponds to the coefficients

which weight each time t.

3 METHOD

Due to the variable genotype length approach,

several features were introduced apart from the

general search strategies described before.

Firstly, each individual can have different

lengths. This feature determines the mutation and

crossover operators, so the generic DE operators

must be changed as it is explained bellow.

With respect to the mutation operator, it includes

arithmetic operations to be executed over individuals

with different lengths. So, the following

considerations must be taken into account:

 The smallest individuals will be completed with

zeros until they reach the length of the

corresponding individual which will be added,

subtracted or multiplied to. By completing with

zeros, the resultant vector does not differ so much

with respect to its predecessors.

 Once the mutant vector is obtained, a mutation

length operator is applied with the aim of avoiding

the length increase resulting from the previous step.

This way, the mutant vector can keep or increase or

decrease its length in one unit. This new cell will

contain a random value. In future experiments, the

number of cells increased/decreased will be

introduced as a parameter in order to find the best

value.

A general scheme of the proposed mutation

scheme can be seen in Figure 1.

The crossover operator completes the length of

the target vector until the length of the target vector

is reached.

The selection operator is performed as it has

been explained before. The fitness function

penalizes the longest individuals adding the length

of the individual (weighted by an experimental

value) to the MSE. Longer individuals make the

equation more complex. Thus, small individuals are

more.

ICEC 2010 - International Conference on Evolutionary Computation

208

Figure 1: General scheme of the mutation process.

4 RESULTS

4.1 Problem Description

The method developed in this work was applied to

the field of Hydrology, more specifically, to the

prediction of the flow rate resulting from the rain.

Before explaining the results, several concepts must

be introduced (Dorado et al., 2003):

 A river basin is an area drained by rivers and

tributaries. In the case of an urban basin, the streams

and rivers are replaced by a sewage system.

 Run-off is the amount of rainfall that is carried

away from the river basin by streams and rivers.

 The modelling of the run-off flow in a typical

urban basin is that part of hydrology which aims to

model sewage networks. Its objective is to predict

the risk of rain conditions for the basin and to sound

an alarm to protect from flooding or from

subsidence.

In general, the goal of this type of problem is to

predict and model the flow of a typical urban basin

from the rain collected by a sensor. The transference

function between the rainfall and the runoff has

many different conditions, as street slopes or roof

types. The system is of such variability that it

becomes impossible to define an equation capable of

modelling the course of a drop of water from the

moment it falls to the instant in which it enters the

drain network. The course of water through the

network is quite complex and, although there are

equations for modelling it, they are subject to the use

of adjustment parameters which make them depend

on a calibration process.

There are several methods for calculating the

rainfall-runoff process (Viessmann et al., 1989).

One family is based on the use of transfer

functions, usually called “unit hydrographs”

(Hydroworks, 1995).

Another approach is based on hydraulic

equations, whose parameters are fixed by the

morphologic characteristics of the study area

(kinematic wave). Commercial packs for calculating

sewage networks usually provide both “unit

hydrographs” and “kinematic wave” modules.

The use of calculation methods not based on

physics equations, such as Artificial Neural

Networks and Genetic Programming (Drecourt,

1999), is becoming widespread in various civil and

hydraulic engineering fields.

In order to make a solution for this problem, we

use a variant of an Autoregressive Moving Average

Model.







∑













∑











 (3)

As we can see in (3) we need to search for the

optimal values of p (size of the input time window)

and q (size of the output time window) and for the

values of φ and θ coefficients. For this purpose, we

need a variable length codification of this problem.

4.2 Physical Model and Parameter

Configuration

In this work, synthetic data has been generated, by

simulating a rainfall scenario in a physic model done

GENETIC ALGORITHM BASED ON DIFFERENTIAL EVOLUTION WITH VARIABLE LENGTH - Runoff Prediction

on an Artificial Basin

209

to scale. It is placed in the Centre of Technological

Innovation in Civil Engineering (Cea et al., 2009).

This is an experimental model which simulates the

rainfall effect over a metallic structure like a basin.

This way, a superficial runoff is generated. This

experiment has been constructed in order to get an

equation for modelling the rainfall-runoff

transformation and then construct a virtual lab for

runoff predictions. Thereby, real experiments can be

avoided.

The constructed system is composed of these two

parts (Figure 2):

 Metallic structure: with a 2.0x2.5m rectangular

plant. It is composed of three plans with a 5% slope

each (Figure 2).

 Hydraulic system: metallic grid where the system

of rainfall simulation is fixed. It is composed of

polyethylene tubes connected to another one which

supplies the water.

 Equipment for runoff register: test tube for more

than 30 litters which collects the outgoing water.

Figure 2: The experimental design in the laboratory.

The process consists in opening the

dissemination system for a specified period and then

measuring the runoff.

As a result, the two graphics in Figure 3 have

been obtained. The first one represents the rainfall

over the basin and the second one represents the

runoff.

The proposed algorithm has been adapted

according to the problem described before.

Firstly, the individuals were divided in two parts:

one representing the coefficients θ

(i=0..p) and

another one representing the coefficients φ

(j=1..q).

Due to the nature of the problem, it would be

meaningless to combine both parts in the same

evolution process. This way, each individual is

composed of two parts which evolve independently,

but the fitness takes into account both parts together.

Secondly, following the conclusions achieved in

(Qin et al., 2009) and (Mayer et al., 2004) and our

own experiments, the configuration parameters were

set as follows:

 Population size (NP) = 500

 Crossover rate (CR) = 0.3

 Scaling Factor (F) = 0.5

The following strategy belongs to the

RAND/DIR group. Following the nomenclature

used in (Storn and Price, 1997), the chosen strategy

was DE/rand/2/bin. It consists in choosing five

random individuals and operating as follows (4):



,



,

·



,



,





,



,



 (4)

4.3 Discussion

Three different approaches were used in order to

establish a comparison with the method presented in

this paper:

Classical genetic programming (GP): a search

technique proposed by (Koza, 1992). This technique

generates algorithms and expressions represented as

a tree structure. GP has been applied to problems of

rainfall-runoff transformation (Drecourt, 1999), and

it generated complex expressions difficult to

understand.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

m/s

Inputdata

Rainfall

0.00005

0.0001

0.00015

0.0002

0.00025

0.0003

0.00035

0.0004

DesiredOutputData

Run‐off

Figure 3: Input and output of the simulation.

ICEC 2010 - International Conference on Evolutionary Computation

210

 Clonal Selection Algorithms (CSAs): these

algorithms are a type of Artificial Immune Systems

(AIS) (Bownlee, 2007). They are based on Burnet’s

clonal selection theory (Burnet, 1959; Burnet, 1976;

Burnet, 1978), which is inspired by Darwin’s theory

of natural selection to explain the diversity and

adaptability of life. This type of algorithm is

primarily focused on mimicking the clonal selection

principle, which is composed of three mechanisms:

clonal selection, clonal expansion and affinity

maturation via somatic hypermutation. The

implementation used was the Optimization

Immunological Algorithm (opt-IA) proposed in

(Cutello et al., 2004), as it has proved to have a good

performance in optimization problems (Cutello et

al., 2005). To the authors’ knowledge, this technique

has not been applied to rainfall-runoff

transformation problems before. This technique

returns a list of coefficients part of a formula, which

can be easily used to predict outputs.

 Hydrographs: this technique was explained

before, as a typical approach used for calculating

rainfall prediction.

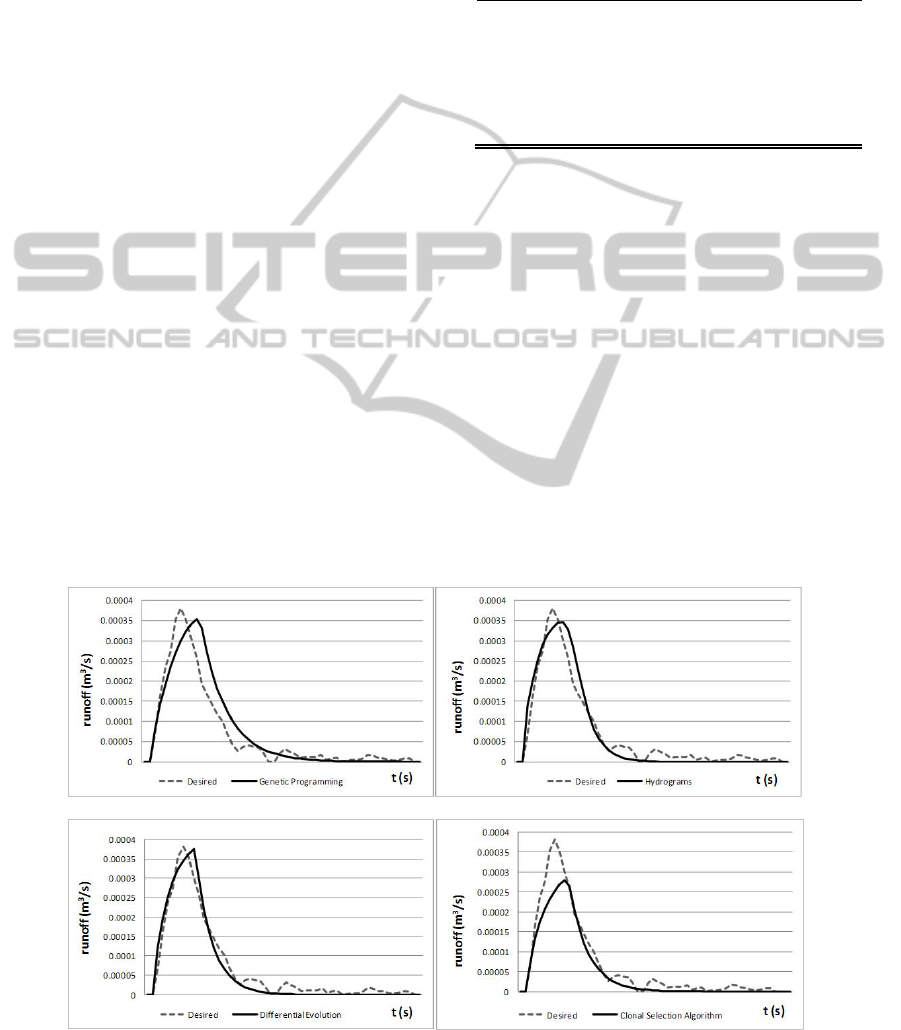
As it can be seen in Figure 4, the proposed method

fits the desired signal better than the other

approaches. In fact, if the Mean Square Error

obtained by these techniques is compared, the lowest

value is reached with the DE approach proposed in

this work.

The HEC-HMS software (HEC-HMS, 2010) has

been used to calculate the hydrographs’ MSE. This

software calculates the hydrograph produced by a

basin. With the rainfall and basin data as input, it

generates the output hydrograph in a graph or table.

Table 1: MSE obtained.

Method

MSE

Genetic Programming 2.50E-05

Clonal Selection Algorithm 1.89E-05

Hydrographs 1.79E-05

Differential Evolution

1.58E-05

The results corresponding to genetic

programming have been calculated with the

algorithm proposed in (Rabuñal et al., 2007).

The following equation (5) has been obtained by

applying the proposed algorithm to the described

data. Table 1 and Figure 4 show the results.





1.025·



0.463·





0.579·



0.119·



(5)

5 CONCLUSIONS

The main objective of this work has been the

construction of a virtual laboratory for calculating

the rainfall-runoff transformation without building a

physical model.

Figure 4: Rainfall-Runoff transformation predicted with the different techniques.

GENETIC ALGORITHM BASED ON DIFFERENTIAL EVOLUTION WITH VARIABLE LENGTH - Runoff Prediction

on an Artificial Basin

211

This way, an equation will be calculated in order

to predict a run-off value using previous rainfall

values.

Several approaches try to solve this problem in

different ways. In this article, a Differential

Evolution technique is proposed. The main included

feature is the variable length of the individuals in the

genetic population.

The results obtained have been compared with

three different techniques used for predicting the

rainfall-runoff transformation. The presented

approach gets good results.

ACKNOWLEDGEMENTS

This work was supported by the General Directorate

of Research, Development and Innovation

(Dirección Xeral de Investigación,

Desenvolvemento e Innovación) of the Xunta de

Galicia (Ref. 08MDS003CT). The work of Vanessa

Aguiar is supported by a grant from the General

Directorate of Research, Development and

Innovation of the Xunta de Galicia.

REFERENCES

Bownlee, J., 2007. Clonal Selection Algorithms, Complex

Intelligent Systems Laboratory (CIS), Centre for

Information Technology Research (CITR), Faculty of

Information and Communication Technologies (ICT),

Swinburne University of Technology, Melbourne,

Australia, pp. 13.

Burnet, F. M., 1959. The clonal selection theory of

acquired immunity. Vanderbilt University Press,

Nashville, Tenessee.

Burnet, F. M., 1976. A modification of Jerne's theory of

antibody production using the concept of clonal

selection. CA Cancer J Clin 26, 119-21.

Burnet, F. M., Clonal selection and after, in: Bell, G. I., et

al., Eds.), Theoretical Immunology, Marcel Dekker

Inc. 1978, pp. 63-85.

Cea, L., Garrido, M., Puertas, J., 2099. Urban flood

computations from direct precipitation data using a

two-dimensional shallow water model. The 8th

International Conference on Urban Drainage

Modelling. Japón.

Cutello, V., Narzisi, G., Nicosia, G., and Pavone ,M.,

2005. Clonal Selection Algorithms: A Comparative

Case Study Using Effective Mutation Potentials, in:

Jacob, C. and al., e., Eds.), 4th International

Conference on Artificial Immune Systems (ICARIS),

Vol. LNCS 3627. Springer-Verlag, Banff, Alberta,

Canada, pp. 13-28.

Cutello, V., Narzisi, G., Nicosia, G., Pavone, M., and

Sorace, G., 2004. How to Escape Traps using Clonal

Selection Algorithms, 1st International Conference on

Informatics in Control, Automation and Robotics

(ICINCO), Vol. 1. INSTICC Press, Setubal, Portugal,

pp. 322-326.

Dorado, J., Rabuñal, J. R., Pazos, A., Rivero, D. and

Santos, A., 2003. Prediction and modeling of the

rainfall-runoff transformation of a typical urban basin

using ANN and GP. Applied Artificial Intelligence,

vol. 17, pp.329-343.

Drecourt, J. P., 1999. Application of Neural Networks and

Genetic Programming to Rainfall-Runoff Modelling.

D2K Technical Report, vol. 0699-1-1, Danish

Hydraulic Institute, Denmark.

Feoktistov, V., 2006. Differential Evolution. In search of

solutions. Springer.

Hydroworks, 1995. User Manual. Hydraulic Research Ltd:

Wallingford.

HEC-HMS, http://www.hec.usace.army.mil/software/hec-

hms/, Accedida por última vez: Abril 2010.

Koza, J. R., 1992. Genetic Programming. On the

Programming of Computers by means of Natural

Selection. Cambrige, MA: The MIT Press.

Mayer, D. G., Kinghorn, B. P. and Archer, A. A.,

Differential evolution – an easy and efficient

evolutionary algorithm for model optimization,

Agricultural Systems, vol. 83, pp. 315-328, 2004.

Qin, A. K., Huang, V. L. and Suganthan, P. N., 2009.

Differential Evolution Algorithm with strategy

adaptation for global numerical optimization, IEEE

Trans. On Evolutionary Computation, vol. 13, no. 2,

pp. 398-417.

Rabuñal, J. R., Puertas, J., Suárez, J., Rivero, D., 2007.

Determination of the unit hydrograph of a typical

urban basin using genetic programming and artificial

neural networks. Hydrological Processes, vol. 21, pp.

476-485.

Storn, R. and Price, K. V., 1997. Differential evolution-A

simple and efficient heuristic for global optimization

over continuous Spaces, J. Global Optim., vol. 11, pp.

341-359.

Viessmann, W., Lewis, G. L. and Knapp, J. W., 1989.

Introduction to Hydrology. New York: Harper Collins.

ICEC 2010 - International Conference on Evolutionary Computation

212