COEVOLUTIONARY ARCHITECTURES WITH STRAIGHT LINE

PROGRAMS FOR SOLVING THE SYMBOLIC REGRESSION

PROBLEM

Cruz Enrique Borges, C´esar L. Alonso

∗

, Jos´e Luis Monta˜na

Departamento de Matem´aticas, Estad´ıstica y Computaci´on, Universidad de Cantabria, 39005 Santander, Spain

∗

Centro de Inteligencia Artiﬁcial, Universidad de Oviedo, Campus de Viesques, 33271 Gij´on, Spain

Marina de la Cruz Echeand´ıa, Alfonso Ortega de la Puente

Departamento de Ingenier´ıa Inform´atica, Escuela Polit´ecnica Superior, Universidad Aut´onoma de Madrid, Madrid, Spain

Keywords:

Genetic programming, Straight-line programs, Coevolution, Symbolic regression.

Abstract:

To successfully apply evolutionary algorithms to the solution of increasingly complex problems we must de-

velop effective techniques for evolving solutions in the form of interacting coadapted subcomponents. In this

paper we present an architecture which involves cooperative coevolution of two subcomponents: a genetic pro-

gram and an evolution strategy. As main difference with work previously done, our genetic program evolves

straight line programs representing functional expressions, instead of tree structures. The evolution strategy

searches for good values for the numerical terminal symbols used by those expressions. Experimentation has

been performed over symbolic regression problem instances and the obtained results have been compared

with those obtained by means of Genetic Programming strategies without coevolution. The results show that

our coevolutionary architecture with straight line programs is capable to obtain better quality individuals than

traditional genetic programming using the same amount of computational effort.

1 INTRODUCTION

Coevolutionary strategies can be considered as an in-

teresting extension of the traditional evolutionary al-

gorithms. Basically, coevolution involvestwo or more

evolutionary processes with interactive performance.

Initial ideas on modelling coevolutionary processes

were formulatedin (Maynard, 1982), (Axelrod, 1984)

or (Hillis, 1991). A coevolutionary strategy consists

in the evolution of separate populations using their

own evolutionary parameters (i.e. genotype of the in-

dividuals, recombination operators, ...) but with some

kind of interaction between these populations. Two

basic classes of coevolutionary algorithms have been

developed: competitive algorithms and cooperative

algorithms. In the ﬁrst class, the ﬁtness of an indi-

vidual is determined by a series of competitions with

other individuals. Competition takes place between

the partial evolutionary processes coevolving and the

success of one implies the failure of the other (see,

for example, (Rosin and Belew, 1996)). On the other

hand, in the second class the ﬁtness of an individual

is determined by a series of collaborations with other

individuals from other populations.

The standard approach of cooperative coevolution

is based on the decomposition of the problem into

several partial components. The structure of each

componentis assigned to a different population. Then

the populations are evolved in isolation from one an-

other but in order to compute the ﬁtness of an individ-

ual from a population, a set of collaborators are se-

lected from the other populations. Finally a solution

of the problem is constructed by means of the combi-

nation of partial solutions obtained from the different

populations. Some examples of application of coop-

erative coevolutionary strategies for solving problems

can be found in (Wiegand et al., 2001) and (Casillas

et al., 2006).

This paper focuses on the design and the study

of several coevolutionary strategies between Ge-

netic Programming (GP) and Evolutionary Algo-

rithms (EA). Although in the cooperative systems the

coevolving populations usually are homogeneous(i.e.

with similar genotype representations), in this case

Enrique Borges C., L. Alonso C., Luis Montaña J., de la Cruz Echeandia M. and Ortega de la Puente A..

COEVOLUTIONARY ARCHITECTURES WITH STRAIGHT LINE PROGRAMS FOR SOLVING THE SYMBOLIC REGRESSION PROBLEM.

DOI: 10.5220/0003075100410050

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 41-50

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

we deal with two heterogeneous populations: one

composed by elements of a structure named straight

line program (slp) that represents programs and the

other one composed by vectors of real constants. The

coevolution between GP and EA was applied with

promising results in (Vanneschi et al., 2001). In that

case a population of trees and another one of ﬁxed

length strings were used.

We have applied the strategies to solve symbolic

regression problem instances. The problem of sym-

bolic regression consists in ﬁnding in symbolic form

a function that ﬁts a given ﬁnite sample set of data

points. More formally, we consider an input space

X = IR

and an output space Y = IR. We are given

a set of m pairs sample z = (x

)

1≤i≤m

. The goal is

to construct a function f : X → Y which predicts the

value y ∈ Y from a given x ∈ X. The empirical error

of a function f with respect to z is:

( f) =

∑

i=1

( f(x

) − y

)

(1)

which is known as the mean square error (MSE).

In our coevolutionary processes for ﬁnding the

function f, the GP will try to guess the shape of the

function whereas the EA will try to adjust the coefﬁ-

cients of the function. The motivation is to exploit the

following intuitive idea: once the shape of the sym-

bolic expression representing some optimal function

has been found, we try to determine the best values of

the coefﬁcients appearing in the symbolic expression.

One simple way to exemplify this situation is the fol-

lowing. Assume that we have to guess the equation

of a geometric ﬁgure. If somebody (for example a GP

algorithm) tells us that this ﬁgure is a quartic func-

tion, it only remains for us to guess the appropriate

coefﬁcients. This point of view is not new and it con-

stitutes the underlying idea of many successful meth-

ods in Machine Learning that combine a space of hy-

potheses with least square methods. Previous work in

which constants of a symbolic expression have been

effectively optimized has also dealt with memetic al-

gorithms, in which classical local optimization tech-

niques as gradient descent (Topchy and Punch, 2001),

linear scaling (Keijzer, 2003) or other methods based

on diversity measures (Ryan and Keijzer, 2003) were

used.

The paper is organized as follows: section 2 pro-

vides the deﬁnition of the structure that will represent

the programs and also includes the details of the de-

signed GP algorithm. In section 3 we describe the

EA for obtaining good values for the constants. Sec-

tion 4 presents the cooperative coevolutionary archi-

tecture used for solving symbolic regression problem

instances. In section 5 an experimental comparative

study of the performanceof our coevolutionarystrate-

gies is done. Finally, section 6 draws some conclu-

sions and addresses future research directions.

2 GP WITH STRAIGHT LINE

PROGRAMS

In the GP paradigm, the evolved computer programs

are usually represented by directed trees with or-

dered branches (Koza, 1992). We use in this paper

a structure for representing programs called straight

line program (slp). A slp consists of a ﬁnite se-

quence of computational assignments where each as-

signment is obtained by applying some function to a

set of arguments that can be variables, constants or

pre-computed results. The slp structure can describe

complex computable functions using less amount of

computational resources than GP-trees, as they can

reuse previously computed results during the evalu-

ation process. Now follows the formal deﬁnition of

this structure.

Deﬁnition. Let F = { f

,..., f

} be a set of functions,

where each f

has arity a

, 1 ≤ i ≤ n, and let T =

,...,t

} be a set of terminals. A straight line pro-

gram (slp) over F and T is a ﬁnite sequence of com-

putational instructionsΓ = {I

,...,I

}, where for each

k ∈ {1,...,l}, I

≡ u

:= f

(α

,...,α

);with f

∈

F, α

∈ T for all i if k = 1 and α

∈ T ∪ {u

,...,u

k−1

}

for 1 < k ≤ l.

The set of terminals T satisﬁes T = V ∪ C where

V = {x

,...,x

} is a ﬁnite set of variables and C =

,...,c

} is a ﬁnite set of constants. The number of

instructions l is the length of Γ.

Observe that a slp Γ = {I

,...,I

} is identiﬁed

with the set of variables u

that are introduced by

means of the instructions I

. Thus the slp Γ can be de-

noted by Γ = {u

,...,u

}. Each of the non-terminal

variables u

represents an expression over the set of

terminals T constructed by a sequence of recursive

compositions from the set of functions F.

An output set of a slp Γ = {u

,...,u

} is any

set of non-terminal variables of Γ, that is O(Γ) =

,...,u

}. Provided that V = {x

,...,x

} ⊂ T is

the set of terminal variables, the function computed

by Γ, denoted by Φ

: I

→ O

, is deﬁned recursively

in the natural way and satisﬁes Φ

,...,a

) =

,...,b

), where b

stands for the value of the ex-

pression overV of the non-terminal variable u

when

we substitute the variable x

by a

; 1 ≤ k ≤ p.

Example. Let F be the set given by the three binary

standard arithmetic operations, F = {+,−, ∗} and let

T = {1, x

} be the set of terminals. In this situation

ICEC 2010 - International Conference on Evolutionary Computation

any slp over F and T is a ﬁnite sequence of instruc-

tions where each instruction represents a polynomial

in two variables with integer coefﬁcients. If we con-

sider the following slp Γ of length 5 with output set

O(Γ) = {u

Γ ≡











:= x

+ 1

:= u

∗ u

:= x

+ x

:= u

∗ u

:= u

− u

(2)

the function computed by Γ is the polynomial

= 2x

+ 1)

− 2x

Straight line programs have a large history in the

ﬁeld of Computational Algebra. A particular class

of straight line programs, known in the literature as

arithmetic circuits, constitutes the underling compu-

tation model in Algebraic Complexity Theory (Bur-

guisser et al., 1997). They have been used in lin-

ear algebra problems (Berkowitz, 1984), in quantiﬁer

elimination (Heintz et al., 1990) and in algebraic ge-

ometry (Giusti et al., 1997). Recently, slp’s have been

presented as a promising alternative to the trees in the

ﬁeld of Genetic Programming, with a good perfor-

mance in solving some regression problem instances

(Alonso et al., 2008). A slp Γ = {u

,...,u

} over F

and T with output set O(Γ) = {u

} could also be con-

sidered as a grammar with T ∪ F as the set of termi-

nals, {u

,...,u

} as the set of variables, u

the start

variable and the instructions of Γ as the rules. This

grammar only generates one word that is the expres-

sion represented by the slp Γ. Note that this is not

exactly Grammar Evolution (GE). In GE there is a

user speciﬁed grammar and the individuals are inte-

ger strings which code for selecting rules from the

provided grammar. In our case each individual is a

context-free grammar generating a context-free lan-

guage of size one.

Hence we will work with slp’s over a set F of

functions and a set T of terminals. The elements of T

that are constants, i.e. C = {c

,...,c

}, they are not

ﬁxed numeric values butreferences to numeric values.

Hence, specializing each c

to a ﬁxed value we obtain

a speciﬁc slp whose corresponding semantic function

is a candidate solution for the problem instance.

For constructing each individual Γ of the initial

population, we adopt the following process: for each

instruction u

∈ Γ ﬁrst an element f ∈ F is ran-

domly selected and then the function arguments of

f are also randomly chosen in T ∪ {u

,...,u

k−1

} if

k > 1 and in T if k = 1. We will consider popula-

tions with individuals of equal length L, where L is

selected by the user. In this sense, note that given a

slp Γ = {u

,...,u

} and L ≥ l, we can construct the

slp Γ

′

= {u

,...,u

l−1

′

,...,u

′

L−1

′

}, whereu

′

= u

and u

′

, for k ∈ {l,. . . ,L−1}, is any instruction. If we

consider the same output set for Γ and Γ

′

is easy to see

that they represent the same function, i.e. Φ

≡ Φ

′

Given a symbolic regression problem instance

with a sample set z = (x

) ∈ IR

× IR, 1 ≤ i ≤ m,

and let Γ be a speciﬁc slp over F and T obtained by

means of the specialization of the constant references

C = {c

,...,c

}. In this situation, the ﬁtness of Γ is

deﬁned by the following expression:

(Γ) = ε

(Φ

) =

∑

i=1

(Φ

) − y

)

(3)

That is, the ﬁtness is the empirical error of the

function computed by Γ, with respect to the sample

set of data points z.

We will use the following recombination opera-

tors for the slp structure.

slp-crossover. Let Γ = {u

,...,u

} and Γ

′

= {u

′

...,u

′

} be two slp’s over F and T. For the construc-

tion of an offspring, ﬁrst a position k in Γ is randomly

selected; 1 ≤ k ≤ L. Let S

= {u

,...,u

} be the set

of instructions of Γ involved in the evaluation of u

Assume that j

< ... < j

. Next we randomly select a

position t in Γ

′

with m ≤ t ≤ L and we substitute in Γ

′

the subset of instructions {u

′

t−m+1

,...,u

′

} by the in-

structions of Γ in S

suitably renamed. The renaming

function R applied to the elements of S

is deﬁned

as R (u

) = u

′

t−m+i

, for all i ∈ {1,...,m}. With this

process we obtain the ﬁrst offspring of the crossover

operation. For the second offspring we analogously

repeat this strategy, but now selecting ﬁrst a position

′

in Γ

′

The underlying idea of the slp-crossover is to in-

terchange subexpressions between Γ and Γ

′

. The fol-

lowing example illustrates this fact.

Example. Let us consider two slp’s:

Γ ≡











:= x+ y

:= u

∗ u

:= u

∗ x

:= u

+ u

:= u

∗ u

′

≡











:= x∗ x

:= u

+ y

:= u

+ x

:= u

∗ x

:= u

+ u

If k = 3 then S

= {u

} (in bold font). t must be

selected in {2,. . . , 5}. Assumed that t = 3, then the

ﬁrst offspring is:

≡











:= x∗ x

:= x+ y

:= u

∗ x

:= u

∗ x

:= u

+ u

that contains the subexpression of Γ represented by

, and the rest of its instructions are taked from Γ

′

COEVOLUTIONARY ARCHITECTURES WITH STRAIGHT LINE PROGRAMS FOR SOLVING THE SYMBOLIC

REGRESSION PROBLEM

For the second offspring, if the selected position in Γ

′

is k

′

= 4, then S

= {u

}. Now if t

′

= 5, the

second offspring is:

≡











:= x+ y

:= u

∗ u

:= x∗ x

:= u

+ y

:= u

∗ x

Mutation. When mutation is applied to a slp Γ, the

ﬁrst step consists in selecting an instruction u

∈ Γ at

random. Then a new random selection is made within

the argumentsof the function f ∈ F that appears in the

instruction u

. Finally the selected argument is substi-

tuted by another one in T ∪ {u

,...,u

i−1

} randomly

chosen.

As it is well known, the reproduction operation

applied to an individual returns an exact copy of the

individual.

3 THE EA TO ADJUST THE

CONSTANTS

In this section we describe an EA that provides

good values for the numeric terminal symbols C =

,...,c

} appearing in the populations of slp’s that

evolve during the GP process. Assume a population

P = {Γ

,...,Γ

} constituted by N slp’s over F and

T = V ∪C. Let [a,b] ⊂ IR be the search space for the

constants c

, 1 ≤ i ≤ q. In this situation, an individual

c is represented by a vector of ﬂoating point numbers

in [a,b]

There are several ways of deﬁning the ﬁtness of

a vector of constants c, but in all of them the cur-

rent population P of slp’s that evolves in the GP pro-

cess is needed. So, given a sample set z = (x

) ∈

×IR, 1 ≤ i ≤ m, thatdeﬁnes a symbolic regression

instance, and given a vector of valuesfor the constants

c = (c

,...,c

), we could deﬁne the ﬁtness of c with

the following expression:

(Γ

); 1 ≤ i ≤ N} (4)

where F

(Γ

) is computed by equation 3 and repre-

sents the ﬁtness of the slp Γ

after the specialization

of the references in C to the corresponding real values

of c.

Observe that when the ﬁtness of c is computed by

means of the above formula, the GP ﬁtness values of

a whole population of slp’s are also computed. This

could be a lot of computational effort when the size

of both populations increases. In order to prevent the

above situation new ﬁtness functionsfor c can be con-

sidered, where only a subset of the population P of

the slp’s is evaluated. Previous work in cooperative

coevolutionary architecturessuggests two basic meth-

ods for selecting the subset of collaborators (Wiegand

et al., 2001): The ﬁrst one in our case consists in the

selection of the best slp of the current population P

corresponding the GP process. The second one se-

lects two individuals from P: the best one and a ran-

dom slp.

Crossover. We will use arithmetic crossover (Schwe-

fel, 1981). Thus, in our EA, the crossover of two indi-

viduals c

and c

∈ [a,b]

produces two offsprings c

′

and c

′

which are linear combinations of their parents.

′

= λ·c

+(1−λ)·c

; c

′

= λ·c

+(1−λ)·c

(5)

In our implementation we randomly choose λ ∈

(0,1) for each crossover operation.

Mutation. A non-uniform mutation operator adapted

to our search space [a,b]

, which is convex, is used

(Michalewiczet al., 1994). The following expressions

deﬁne our mutation operator, with p = 0.5.

t+1

= c

+ ∆(t,b− c

), with probability p (6)

and

t+1

= c

− ∆(t,c

− a), with probability 1− p (7)

k = 1,...,q and t is the current generation. The func-

tion ∆ is deﬁned as ∆(t,y) = y · r · (1 −

) where r

is a random number in [0,1] and T represents the

maximum number of generations. Note that function

∆(t,y) returnsa value in [0,y] such that the probability

of obtaining a value of ∆(t,y) close to zero increases

as t increases. Hence the mutation operator searchs

the space uniformly initially (when t is small), and

very locally at later stages.

In our EA we will use q-tournament as the selec-

tion procedure.

4 THE COEVOLUTIONARY

ARCHITECTURE

In our case the EA for tuning the constants is subor-

dinated to the main GP process with the slp’s. Hence,

several collaborators are used during the computation

of the ﬁtness of a vector of constants c, whereas only

the best vector of constants is used to compute the ﬁt-

ness of a population of slp’s.

A basic cooperative coevolutionary strategy be-

gins with the initialization of both populations. First

the ﬁtness of the individuals of the slp’s population

are computed considering a randomly selected vector

of constants as collaborator. Then alternative genera-

tions of both cooperative algorithms in a round-robin

ICEC 2010 - International Conference on Evolutionary Computation

fashion are performed. This strategy can be general-

ized in a natural way by the execution of alternative

turns of both algorithms. We will consider a turn as

the isolated and uninterrupted evolution of one popu-

lation for a ﬁxed number of generations. Note that if

a turn consists of only one generation we obtain the

basic strategy. We display below the algorithm de-

scribing this cooperative coevolutionary architecture:

begin

Pop_slp := initialize_GP-slp_population

Pop_const := initialize_EA-constants_population

Const_collabor := random(Pop_const)

evaluate(Pop_slp,Const_collabor)

While (not termination condition) do

Pop_slp := turn_GP(Pop_slp,Const_collabor)

Collabor_slp := {best(Pop_slp),

random(Pop_slp)}

Pop_const := turn_EA(Pop_const,Collabor_slp)

Const_collabor := best(Pop_const)

end

5 EXPERIMENTATION

5.1 Experimental Settings

The experimentation consists in the execution of the

proposed cooperative coevolutionary strategies, con-

sidering several types of target functions. Two exper-

iments were performed.

For the ﬁrst experiment two groups of tar-

get functions are considered: the ﬁrst group in-

cludes 100 randomly generated univariate polyno-

mials whose degrees are bounded by 5 and the

second group consists of 100 target functions rep-

resented by randomly generated slp’s over F =

{+,−,∗, /,sqrt,sin,cos,ln,exp} and T = {x,c}, c ∈

[−1,1], with length 16. We will name this second

group “target slp’s”.

A second experiment is also performed solving

symbolic regression problem instances associated to

the following three multivariate functions:

(x,y,z) = (x+ y+ z)

+ 1 (8)

(x,y,z,w) =

w (9)

(x,y) = x y+ sin((x− 1) (y+ 1)) (10)

For every execution the sample set is constituted

by 30 points. In the case of the functions that belong

to the ﬁrst experiment, the sample points are in the

range [−1, 1]. For the functions f

and f

the points

are in the range [−100,100] for all variables. Finally

function f

varies in the range [−3,3] along each axis.

The individuals are slp’s over F =

{+,−,∗, /,sqrt} in the executions related to the

100 generated polynomials and to the functions f

and f

. The function set F is incremented with the

operation sin for the problem instance associated to

and also with the operations cos, ln and exp for

the group of target slp’s.

Besides the variables, the terminal set also in-

cludes two referencesto constants for thepolynomials

and only one reference to a constant for the rest of the

target functions. The constants take values in [−1,1].

The particular settings for the parameters of the

GP process are the following: population size: 200,

crossover rate: 0.9, mutation rate: 0.05, reproduc-

tion rate: 0.05, 5-tournament as selection procedure

and maximum length of the slp’s: 16. In the case of

the EA that adjusts the constants, the population in-

cludes 100 vector of constants, crossover rate: 0.9,

mutation rate: 0.1 and 2-tournament as selection pro-

cedure. For all the coevolutionary strategies, the com-

putation of the ﬁtness of an slp during the GP process

will use the best vector of constants as collaborator,

whereas in order to compute the ﬁtness of a vector of

constants in the EA process, we consider a collabo-

rator set containing the best slp of the population and

another one randomly selected. Both processes are

elitist and a generational replacement between pop-

ulations is used. But in the construction of the new

population, the offsprings generated do not necessar-

ily replace their parents. After a crossover we have

four individuals: two parents and two offsprings. We

select the two best individuals with different ﬁtness

values. Our motivation is to prevent premature con-

vergence and to maintain diversity in the population.

We compare the standard GP-slp strategy with-

out coevolution with three coevolutionary strategies

that follow the general architecture described in sec-

tion 4. We have implemented and executed over the

same sets of problem instances, the well known GP-

tree strategy with the standard recombination opera-

tors. Thus the obtained results are included in the

comparative study.

The ﬁrst coevolutionary strategy, named Basic

GP-EA (BGPEA), consists in the alternative execu-

tion of one generation of each cooperative algorithm.

The second strategy, named Turns GP-EA (TGPEA),

generalizes BGPEA by means of the execution of al-

ternative turns of each algorithm. Finally, the third

strategy executes ﬁrst a large turn of the GP algo-

rithm with the slp’s and then follows the execution

of the EA related with the constants until termination

condition was reached. This strategy is named Sep-

arated GP-EA (SGPEA). In the case of TGPEA we

have considered a GP turn as the evolution of the pop-

ulation of slp’s during 25 generations. On the other

hand, an EA turn consists of 5 generations in the evo-

COEVOLUTIONARY ARCHITECTURES WITH STRAIGHT LINE PROGRAMS FOR SOLVING THE SYMBOLIC

REGRESSION PROBLEM

lution of the population related to the constants. In

SGPEA strategy we divide the computational effort

between the two algorithms: 90% for GP and 10%

for EA. The computational effort (CE) is deﬁned as

the total number of basic operations that have been

computed up to that moment.

In the ﬁrst experiment one execution for each

strategy has been performed over the 200 generated

target functions. On the other hand, in the second ex-

periment we have executed all strategies 100 times for

each of the three multivariate functions f

, f

and f

For all the executions the evolution ﬁnished after 10

basic operations have been computed.

5.2 Experimental Results

Frequently, when different Genetic Programming

strategies for solving symbolic regression instances

are compared, the quality of the ﬁnal selected model

is evaluated by means of its corresponding ﬁtness

value over the sample set. But with this quality mea-

sure it is not possible to distinguish between good

executions and overﬁting executions. Then it makes

sense to consider another new set of unseen points,

called the validation set, in order to give a more

appropriate indicator of the quality of the selected

model. So, let (x

)

1≤i≤n

test

a validation set for the

target function g(x) (i.e. y

= g(x

)) and let f(x) be

the model estimated from the sample set. Then the

validation ﬁtness vf

test

is deﬁned by the mean square

error (MSE) between the values of f and the true val-

ues of the target function g over the validation set:

test

∑

i=1

( f(x

) − y

)

(11)

An execution will be considered successful if the

ﬁnal selected model f has validation ﬁtness less than

10% of the range of the sample set z = (x

)

1≤i≤30

That is:

test

≤ 0.1



max

1≤i≤30

− min

1≤i≤30



(12)

On the other hand, an execution will be spurious

if the validation ﬁtness of the selected model veriﬁes:

test

≥ 1.5|Q

− Q

| (13)

Were Q

and Q

represent, respectively, the ﬁrst and

third quartile of the empirical distribution of the exe-

cutions in terms of the validation ﬁtness. The spurious

executions will be removed from the experiment.

In what follows we shall present a complete statis-

tical comparative study about the performance of the

described coevolutionary strategies. For both experi-

ments we will show the empirical distribution of the

Table 1: Spurious and success rates for each strategy and

group of target functions.

[X] spurious success

SGPEA 13% 100%

TGPEA 8% 99%

BGPEA 11% 100%

GP− slp 12% 100%

GP−tree 12% 100%

SLP(F,T) spurious success

SGPEA 16% 98%

TGPEA 13% 99%

BGPEA 13% 98%

GP− slp 14% 96%

GP−tree 14% 99%

non-spurious executions as well as the values of the

mean, variance, median, worst and best execution in

terms of the validation ﬁtness. We also present sta-

tistical hypothesis tests in order to determine if some

strategy is better than the others. We consider a val-

idation set of 200 new and unseen points randomly

generated.

5.2.1 Experiment 1

We shall denote the polynomial set as P

[X] and the

set of target slp’s over F and T as SLP(F,T). Table

1 displays for each strategy the spurious and success

rates of the executions. Note that the success rate

is computed after removing the spurious executions.

Figure 1 presents the empirical distribution of the ex-

ecutions over the two groups of generated target func-

tions. This empirical distribution is displayed using

standard box plot notation with marks at best execu-

tion, 25%, 50%, 75% and worst execution, consider-

ing the validation ﬁtness of the selected model. Ta-

ble 2 speciﬁes the values of the validation ﬁtness for

the worst, median and best execution. Finally Table 3

shows the means an variances. Note that for these two

groups of functions one execution per target function

was performed.

Analyzing the information given by the above ta-

bles and ﬁgure we could deduce the following facts:

1. All methods have a similar rate of spurious execu-

tions and also the success rate is almost equal for

all strategies.

2. The empirical distributions of the non-spurious

runs are again very similar for all the studied

strategies. Probably for the group of polynomials,

SGPEA is slightly better than the others. Observe

in ﬁgure 1 that this strategy has the corresponding

box smaller and a little below than the other meth-

ods. SGPEA also has the best mean and variance

ICEC 2010 - International Conference on Evolutionary Computation

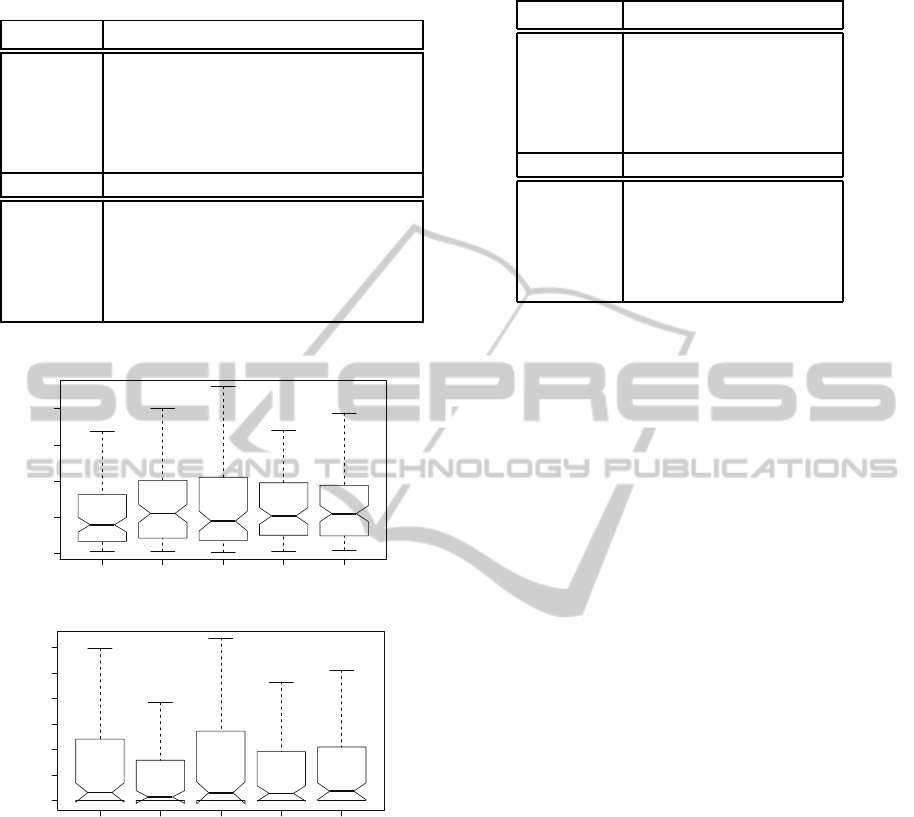
Table 2: Minimal, median and maximal values of the vali-

dation ﬁtness for each method and group of target functions.

[X] min med max

SGPEA 3.25· 10

−3

3.33· 10

−2

0.17

TGPEA 2.27· 10

−3

4.58· 10

−2

0.2

BGPEA 1.25· 10

−3

3.58· 10

−2

0.23

GP− slp 2.26· 10

−3

4.48· 10

−2

0.17

GP−tree 4.64· 10

−3

4.42· 10

−2

0.19

SLP(F,T) min med max

SGPEA 0 1.6· 10

−3

0.12

TGPEA 0 1.66· 10

−3

7.69· 10

−2

BGPEA 0 2.84· 10

−3

0.13

GP− slp 0 1.61· 10

−3

9.32· 10

−2

GP−tree 0 4.29· 10

−3

0.1

SGPEA TGPEA BGPEA GP−slp GP−tree

0.00 0.05 0.10 0.15 0.20

Polynomials

SGPEA TGPEA BGPEA GP−slp GP−tree

0.00 0.04 0.08 0.12

slp

Figure 1: Empirical distributions of the non-spurious exe-

cutions for both groups of functions and for each strategy.

values (table 3). Nevertheless for the group of tar-

get slp’s it seems that the best method is TGPEA.

3. All strategies perform quite well over the tar-

get functions of this experiment, specially for the

group of target slp’s. Considering the values of

mean and variance and the fact that for each func-

tion only one execution was performed, probably

the BGPEA method is a little worse than the oth-

ers.

With the objective of justify the comparative quality

of the studied strategies we have made statistical hy-

pothesis tests between them, which results are showed

Table 3: Values of means and variances.

[X] µ σ

SGPEA 4.39· 10

−2

3.83· 10

−2

TGPEA 6.03· 10

−2

5.23· 10

−2

BGPEA 5.49· 10

−2

5.22· 10

−2

GP− slp 5.19· 10

−2

3.82· 10

−2

GP−tree 5.62· 10

−2

4.26· 10

−2

SLP(F,T) µ σ

SGPEA 1.62· 10

−2

2.79· 10

−2

TGPEA 1.14· 10

−2

1.78· 10

−2

BGPEA 1.96· 10

−2

3· 10

−2

GP− slp 1.49· 10

−2

2.33· 10

−2

GP−tree 1.5 · 10

−2

2.23· 10

−2

in table 4. Roughly speaking, the null-hypothesis in

each test with associated pair (i, j) is that strategy i is

not better than strategy j. Hence if value a

of the el-

ement (i, j) in table 4 is less than a signiﬁcance value

α, we can reject the corresponding null-hypothesis.

From the results presented in table 4 and with sig-

niﬁcance values of α between 0.05 and 0.1, we can

conclude that for the group of polynomials the best

strategy is SGPEA whereas there is no clear winner

strategy for the group of target slp’s.

5.2.2 Experiment 2

In this experiment, the multivariate functions de-

scribed by the expressions 8, 9 and 10 have been con-

sidered as target functions. We have performed 100

executions for each strategy and function. In the fol-

lowing tables and ﬁgures we present for the new func-

tions the same results as those presented for the target

functions of experiment 1.

In termsof success rates, the coevolutionarymeth-

ods are of similar performance and they seem to be

better than the standard GP-slp strategy without co-

evolution. Nevertheless we can see that all the strate-

gies outperform the standard GP-tree procedure. This

fact is moreclear after observingin ﬁgure 2 the empir-

ical distributions of the non-spurious executions. For

the multivariate polynomialof degree two, f

, the best

strategy is SGPEA whereas for the linear polynomial

with four variables, TGPEA seems to be better than

the other strategies. In the case of the trigonometric

function f

it is not clear which is the best method.

But in any case, the standard GP-tree method is the

worst of the studied strategies.

In table 6 it can be seen that the validation ﬁt-

ness has a big range, specially for functions f

and

. Hence, the mean and variance, displayed in ta-

ble 7, have also big values for the above two target

functions. Indeed the values are very big for f

, al-

COEVOLUTIONARY ARCHITECTURES WITH STRAIGHT LINE PROGRAMS FOR SOLVING THE SYMBOLIC

REGRESSION PROBLEM

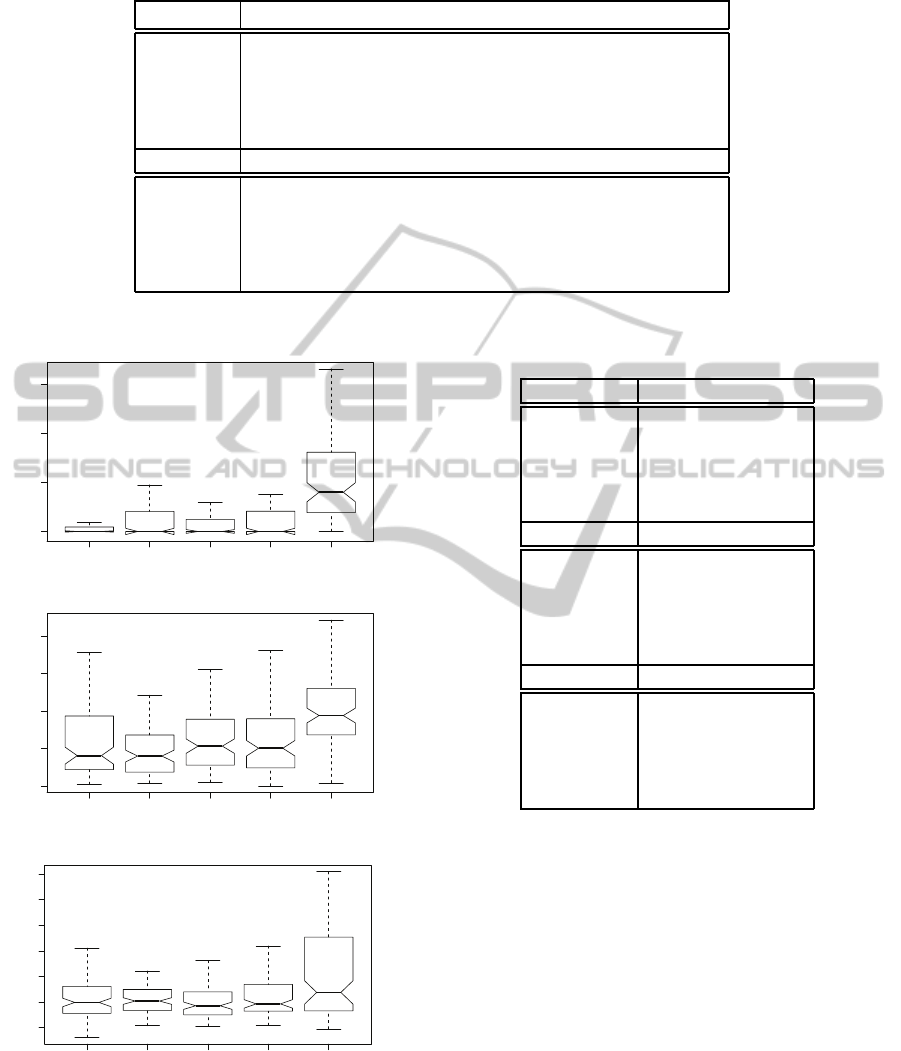
Table 4: Results of the crossed statistical hypothesis tests about the comparative quality of the studied strategies.

[X] SGPEA TGPEA BGPEA GP− slp GP− tree

SGPEA 1 2.51· 10

−2

0.27 8.9· 10

−2

6.1· 10

−2

TGPEA 0.78 1 0.8 0.53 0.45

BGPEA 0.9 0.3 1 0.12 0.17

GP− slp 0.99 0.28 0.59 1 0.4

GP−tree 1 0.61 0.77 0.75 1

SLP(F,T) SGPEA TGPEA BGPEA GP− slp GP− tree

SGPEA 1 0.82 0.44 0.82 0.39

TGPEA 0.54 1 0.14 0.44 0.28

BGPEA 0.99 1 1 0.93 0.7

GP− slp 0.74 0.93 0.49 1 0.39

GP−tree 0.82 0.99 0.49 0.9 1

SGPEA TGPEA BGPEA GP−slp GP−tree

0.0e+00 5.0e+07 1.0e+08 1.5e+08

(x, y, z)

SGPEA TGPEA BGPEA GP−slp GP−tree

0 200 400 600 800

(x, y, z, w)

SGPEA TGPEA BGPEA GP−slp GP−tree

0.4 0.5 0.6 0.7 0.8 0.9 1.0

(x, y)

Figure 2: Empirical distributions of the non-spurious exe-

cutions.

though the best execution over this function has val-

idation ﬁtness equal to zero for all methods. Note

that for the above two functions the points are in the

Table 5: Spurious and success rates of the executions over

the multivariate functions.

(x,y,z) spurious success

SGPEA 25% 74%

TGPEA 13% 69%

BGPEA 19% 66%

GP− slp 11% 62%

GP−tree 5% 12%

(x,y,z,w) spurious success

SGPEA 7% 42%

TGPEA 7% 49%

BGPEA 6% 41%

GP− slp 7% 39%

GP−tree 12% 14%

(x,y) spurious success

SGPEA 8% 100%

TGPEA 14% 100%

BGPEA 9% 100%

GP− slp 9% 100%

GP−tree 20% 100%

range [− 100,100] for all variables. Considering the

results that appear in these two tables, we could say

that the coevolutionary strategies outperform the non-

coevolutionary ones.

Finally, as it was done in experiment 1, we have

made for the three functions the crossed statistical

hypothesis tests between all pairs of the considered

strategies and the results are showed in table 8. Con-

sidering a signiﬁcant value α = 0.05 it seems that

for the function f

SGPEA is the best strategy but

there is no clear winner coevolutionary strategy for

the functions f

and f

. Nevertheless such results con-

ﬁrm that the coevolutionary methods are promising

strategies for solving symbolic regression problem in-

stances and that the slp structure is clearly better for

representing the models than the tree structure.

ICEC 2010 - International Conference on Evolutionary Computation

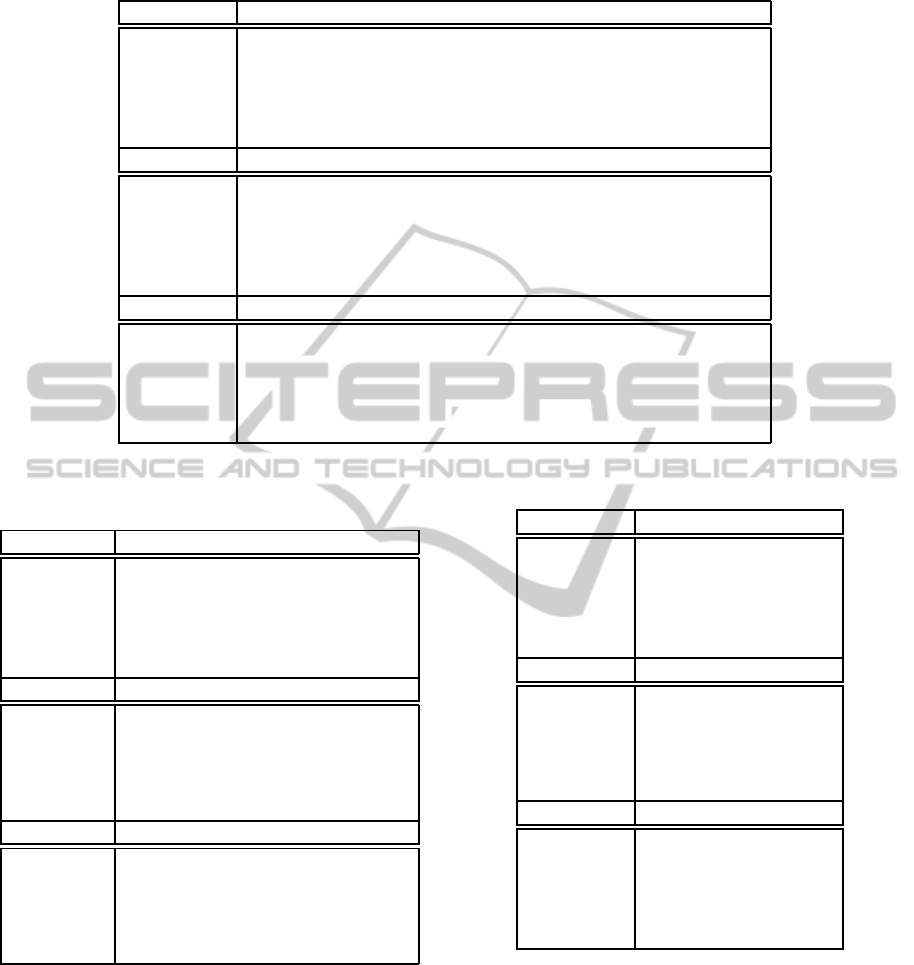
Table 8: Results of the crossed statistical hypothesis tests.

(x,y,z) SGPEA TGPEA BGPEA GP− slp GP−tree

SGPEA 1 3.39· 10

−4

1.41· 10

−3

9.23· 10

−5

4.53· 10

−31

TGPEA 1 1 1 0.44 7.13· 10

−19

BGPEA 0.97 0.12 1 2.66· 10

−2

7.46· 10

−24

GP− slp 0.91 0.43 0.9 1 3.47· 10

−15

GP−tree 1 1 1 1 1

(x,y,z,w) SGPEA TGPEA BGPEA GP− slp GP− tree

SGPEA 1 0.84 0.14 0.16 8.16· 10

−9

TGPEA 0.12 1 2.53· 10

−2

3.07· 10

−2

4.29· 10

−12

BGPEA 0.82 0.91 1 0.67 3.77· 10

−6

GP− slp 0.76 0.84 0.87 1 1.38· 10

−6

GP−tree 1 1 0.99 1 1

(x,y) SGPEA TGPEA BGPEA GP − slp GP− tree

SGPEA 1 0.41 0.96 0.28 2.06· 10

−2

TGPEA 0.32 1 0.84 0.37 5.23· 10

−3

BGPEA 0.35 4.65· 10

−2

1 2.84· 10

−2

1.29· 10

−2

GP− slp 0.44 0.51 0.99 1 5.86· 10

−2

GP−tree 0.93 0.42 0.88 0.34 1

Table 6: Minimal, median and maximal values of the vali-

dation ﬁtness for each method and target function.

(x,y,z) min med max

SGPEA 0 1 94412.42

TGPEA 0 1 4.74· 10

BGPEA 0 1 2.8· 10

GP− slp 0 1 3.75· 10

GP− tree 3.91· 10

−24

3.38· 10

1.65· 10

(x,y,z,w) min med max

SGPEA 10.53 156.64 710.84

TGPEA 17.3 148.17 484.58

BGPEA 21.76 193.92 621.22

GP− slp 2.4 184.95 723.69

GP− tree 18.73 359.32 859.69

(x,y) min med max

SGPEA 0.36 0.49 0.71

TGPEA 0.41 0.49 0.62

BGPEA 0.41 0.48 0.66

GP− slp 0.41 0.48 0.72

GP− tree 0.39 0.51 1.01

6 CONCLUSIONS

We have designed several cooperative coevolution-

ary strategies between a GP and an EA. The genetic

program evolves straight line programs that represent

functional expressions whereas the evolutionary al-

gorithm optimizes the values of the constants used

by those expressions. Experimentation has been per-

formed on several groups of target functions and we

Table 7: Values of means and variances.

(x,y,z) µ σ

SGPEA 1345.95 10899.09

TGPEA 6.11· 10

1.37· 10

BGPEA 1.98· 10

5.09· 10

GP− slp 6.5 · 10

1.11· 10

GP−tree 4.72· 10

4· 10

(x,y,z,w) µ σ

SGPEA 211.05 150.71

TGPEA 175.2 116.59

BGPEA 221.29 133.87

GP− slp 229.7 157.18

GP−tree 362.58 160.8

(x,y) µ σ

SGPEA 0.5 6.41· 10

−2

TGPEA 0.5 4.79· 10

−2

BGPEA 0.49 5.86 · 10

−2

GP− slp 0.51 6.65· 10

−2

GP−tree 0.55 0.13

have compared the performance between the stud-

ied strategies. In all cases the computational ef-

fort is ﬁxed to a maximum number of evaluations.

The quality of the selected model after the execution

was measured considering a validation set of unseen

points randomly generated, instead of the sample set

used for the evolution process. A complete statistical

study of the experimental results has been done. It

has been shown that the coevolutionary architectures

are promising strategies that in many cases are better

than the traditional GP algorithms without coevolu-

COEVOLUTIONARY ARCHITECTURES WITH STRAIGHT LINE PROGRAMS FOR SOLVING THE SYMBOLIC

REGRESSION PROBLEM

tion. We have also conﬁrmed that the straight line

program structure clearly outperforms the traditional

tree structure used in GP to codify the individuals.

In future work we wish to study the behavior of

our coevolutionary model without assuming previous

knowledge of the length of the slp structure. To this

end new recombination operators must be designed.

On the other hand we could include some local search

procedure into the EA that adjusts the constants. Also

the ﬁtness function could be modiﬁed, including sev-

eral penalty terms to perform model regularization

such as complexity regularization using the length of

the slp structure. Finally we might optimize the con-

stants of our slp’s by means of classical local opti-

mization techniques such as gradient descent or linear

scaling, as it was done for tree-based GP in (Keijzer,

2003) and (Topchy and Punch, 2001), and compare

the results with those obtained by the computational

model described in this paper.

ACKNOWLEDGEMENTS

This work is partially supported by spanish grants

TIN2007-67466-C02-02, MTM2004-01167 and

S2009/TIC-1650.

REFERENCES

Alonso, C. L., Montana, J. L., and Puente, J. (2008).

Straight line programs: a new linear genetic program-

ming approach. In Proc. 20th IEEE International

Conference on Tools with Artiﬁcial Intelligence (IC-

TAI), pages 517–524.

Axelrod, R. (1984). The evolution of cooperation. Basic

Books, New York.

Berkowitz, S. J. (1984). On comomputing the determinant

in small parallel time using a small number of pro-

cessors. In Information Processing Letters 18, pages

147–150.

Burguisser, P., Clausen, M., and Shokrollahi, M. A. (1997).

Algebraic Complexity Theory. Springer.

Casillas, J., Cordon, O., Herrera, F., and Merelo, J. (2006).

Cooperative coevolution for learning fuzzy rule-based

systems. In Genetic and Evolutionary Computation

Conference (GECCO 2006), pages 361–368.

Giusti, M., Heintz, J., Morais, J., Morgenstern, J. E., and

Pardo, L. M. (1997). Straight line programs in ge-

ometric elimination theory. In Journal of Pure and

Applied Algebra 124, pages 121–146.

Heintz, J., Roy, M. F., and Solerno, P. (1990). Sur la com-

plexite du principe de tarski-seidenberg. In Bulletin de

la Societe Mathematique de France, 118, pages 101–

126.

Hillis, D. (1991). Co-evolving parasites improve simulated

evolution as an optimization procedure. In Artiﬁcial

Life II, SFI Studies in the Sciences Complexity 10,

pages 313–324.

Keijzer, M. (2003). Improving symbolic regression with

interval arithmetic and linear scaling. In Procceedings

of EuroGP 2003, pages 71–83.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. The MIT Press, Cambridge, MA.

Maynard, J. (1982). Evolution and the theory of games.

Cambridge University Press, Cambridge.

Michalewicz, Z., Logan, T., and Swaminathan, S. (1994).

Evolutionary operators for continuous convex param-

eter spaces. In Proceedings of the 3rd Annual Confer-

ence on Evolutionary Programming, pages 84–97.

Rosin, C. and Belew, R. (1996). New methods for compete-

tive coevolution. In Evolutionary Computation 5 (1),

pages 1–29.

Ryan, C. and Keijzer, M. (2003). An analysis of diversity of

constants of genetic programming. In Procceedings of

EuroGP 2003, pages 409–418.

Schwefel, H. P. (1981). Numerical Optimization of Com-

puter Models. John Wiley and Sons, New-York.

Topchy, A. and Punch, W. F. (2001). Faster genetic pro-

gramming based on local gradient search of numeric

leaf values. In Proceedings of the 2001 conference

on Genetic and Evolutionary Computation (GECCO),

pages 155–162.

Vanneschi, L., Mauri, G., Valsecchi, A., and Cagnoni,

S. (2001). Heterogeneous cooperative coevolution:

Strategies of integration between GP and GA. In Proc.

of the Fifth Conference on Artiﬁcial Evolution (AE

2001), pages 311–322.

Wiegand, R. P., Liles, W. C., and Jong, K. A. D. (2001).

An empirical analysis of collaboration methods in co-

operative coevolutionary algorithms. In Proceedings

of the 2001 conference on Genetic and Evolutionary

Computation (GECCO), pages 1235–1242.

ICEC 2010 - International Conference on Evolutionary Computation