A GENETIC ALGORITHM APPROACH TO A 3D HIGHWAY

ALIGNMENT DEVELOPMENT

Botan M. Ahmad AL-Hadad and Michael Mawdesley

Department of Civil Engineering, University of Nottingham,University Park, Nottingham, U.K.

Keywords: Highway alignment, Genetic algorithms, Optimization.

Abstract: This paper reports for the possibility of developing a genetic algorithm (GA) based technique model to

optimize highway alignment. It suggests a novel technique to optimize a highway alignment in a three

dimensional space. The technique considers station points to simultaneously configure both horizontal and

vertical alignment rather than considering the existing conventional principles of design which deals with

both alignments in two different stages and uses horizontal intersection points (HIP), vertical intersection

points (VIP), tangents (T), curve radii (R), deflection angles (∆), grade values (± g %), and horizontal and

vertical curve fittings to depict the horizontal and vertical alignments. The proposed method is expected to

produce a global optimal or near optimal solution and also to reduce the number of highway alignment

design elements required and consequently reduce the constraints imposed on alignment planning and

design. The results obtained have good merits and encourage further investigations for better solutions.

1 INTRODUCTION

Highway alignment development aims to connect

two terminal points at minimum possible cost

subject to the design, environmental (natural features

and air pollution), economical, social, and political

constraints. The final alignment selection will also

be affected by the public view points and decision

makers’ policy. The most common cost components

that can be considered are construction,

maintenance, location, earthwork, environmental,

and user costs. The weight of each component is

affected by the user and/or designer preferences

and/or the purpose that the alignment is built for.

All these compenents and parameters must be

considered together. However an alignment that

makes one of the parameters optimal will rarely, if

ever, make all optimal. The problem of developing

and selecting an optimum alignment is therefore

very complex but very important.

1.1 The Conventional Approach

In conventional highway design projects, highway

engineers and planners select several candidates as

alternative solutions and evaluate their suitability for

the region’s environment until coming up with the

most suitable one (Wright and Ashford, 1998).

Horizontal and vertical alignments are considered

apart from each other and the vertical one is

optimized based on the ‘best’ selected horizontal

one. This process starts by fixing several horizontal

intersection points (HIP). The number of the HIPs

may depend on the length of the highway, natural

and manmade features, and the topography. The

successive HIPs are then connected by lines thus

forming a horizontal piecewise linear trajectory.

These lines are called tangents and the deflections in

direction between successive tangents at HIPs are

called Deflection angles. Later on and in a separate

procedure horizontal circular or spiral curves are

fitted at each HIP location to form the proposed

horizontal alignment. This alignment then undergoes

an evaluation process to know whether it suits the

environment or not. The evaluation may take the

form of cost consideration, damage to environment,

and socio-economic issues subject to several design

constraints that are imposed on the alignment. This

process, through numerous iterations, is repeated

and should continue until finding the most suitable

one.

In a different process the vertical alignment is

selected using the same concept as for the horizontal

alignment. First, the elevations along the selected

horizontal alignment are determined to form the

natural ground elevation profile (NGE). Later on, to

129

Ahmad AL-Hadad B. and Mawdesley M..

A GENETIC ALGORITHM APPROACH TO A 3D HIGHWAY ALIGNMENT DEVELOPMENT.

DOI: 10.5220/0003060201290136

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 129-136

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

generate the alignment grade line, several vertical

intersection points (VIPs) are fixed and

interconnected successively to form a vertical

piecewise linear trajectory. The number of VIPs is

mainly affected by the variations in ground

elevations. Parabolic curves are then fitted at VIPs to

depict the vertical alignment. The vertical grade line

of the alignment is then evaluated based on the

design requirements and the amounts of earthwork

for both cut and fill sections. The process will

continue repeatedly until finding the most suitable

one.

The selection of the final alternative alignment is

accomplished by focusing on the detailed design

elements. HIPs, deflection angles, curve radii, VIPs,

tangents, grade values, and sight distances are

among the design elements of highway alignment in

3D. Most of these design elements are constrained

by standard limits described by such documents as

the Design Manual for Roads and Bridges (DMRB,

1992-2008) and AASHTO design standards

(AASHTO, 1994).

As the two processes are considered apart from

each other, the generated alignment likely represents

a local optimum rather than a global one. This

approach takes into account many design elements

and, at the same time, neglects numerous possible

solutions due to non simultaneous consideration of

both alignments. This process is also very expensive

in terms of time.

Researchers have tried to speed up the process of

highway alignment planning and design and to find

better solutions. Attempts have been done to

optimize either horizontal or vertical or both

simultaneously. Calculus of variations by Shaw and

Howard (1982), numerical analysis by Chew et al

(1989), linear programming by Easa (1988), and

genetic algorithms by Jong (1998), Fwa et al.

(2002), and Tat and Tao (2003) are some of the

techniques that have been used. The work done by

Jong (1998) has also been extended to incorporate

more cost components, GIS integration, and to

formulate the model to handle the problem as a multi

objective problem. All these can be seen in (Jong

and Schonfeld, 1999) (Jha and Schonfeld, 2000)

(Maji and Jha, 2009). It should be noted that all

these studies are based on the conventional design

principles of highway alignment design which

consider HIP, VIP, tangents, and curve fittings.

Since its introduction, despite the extreme

development in computers and highway surveying

field instruments technologies (e.g. total station),

highway engineers and planners are still using the

same convensional design approach. None of the

studies has exploited the technology development to

explore the possibility of changing some ideas

imposed on highway alignment planning and design.

A question arises here, do we still need to keep the

same planning and design approach or do we need to

change to reflect technology development? That is

the question that this study seeks to answer.

1.2 The New Approach

This study introduces a novel technique for

alignment optimization. It suggests optimizing

simultaneously the horizontal and vertical alignment

of a highway through station points. Station points

as points along the centre line of alignment, which

are defiend by their X, Y, and Z coordinates, are

used to define the alignment configuration. This

research study is inspired by the fact that any

generated alignment by whatever method will finally

consist of a series of station points and it will be

implemented on the ground depending on those

station points. Figure 1 shows the difference in

alignment generation and configuration between the

traditional and proposed method.

In this study GA, as an evolutionary adaptive

search technique (Beasley et al, 1993), is used to

perform the search. Some modifications to suit the

nature of the problem have been included (Davis

1991; Mitchell 1996).

A variety of studies have proven that GA is an

efficient tool for planning and optimization

problems. Mathews et al (1999) applied GA to land

use planning, Mawdesley et al (2002) used GA for

construction site layout in project planning, Ford

(2007) used GA for housing location planning, Jong

(1998), Fwa et al (2002), Tat and Tao (2003), and

Kang (2008) used GA for alignment optimization

problems.

2 THE MODEL FORMULATION

2.1 The Study Boundary

The study area is defined and divided into

rectangular grid cells usually produced from a GIS

model of the area under consideration. The size of

the grid cells falls within the user preferences and

depends on the desired accuracy. Each grid cell may

handle one or more than one average value. In this

study two different values are assigned to each cell.

Average land unit cost values are used for the

alignment location dependent cost calculations while

average ground elevations are used to calculate the

ICEC 2010 - International Conference on Evolutionary Computation

130

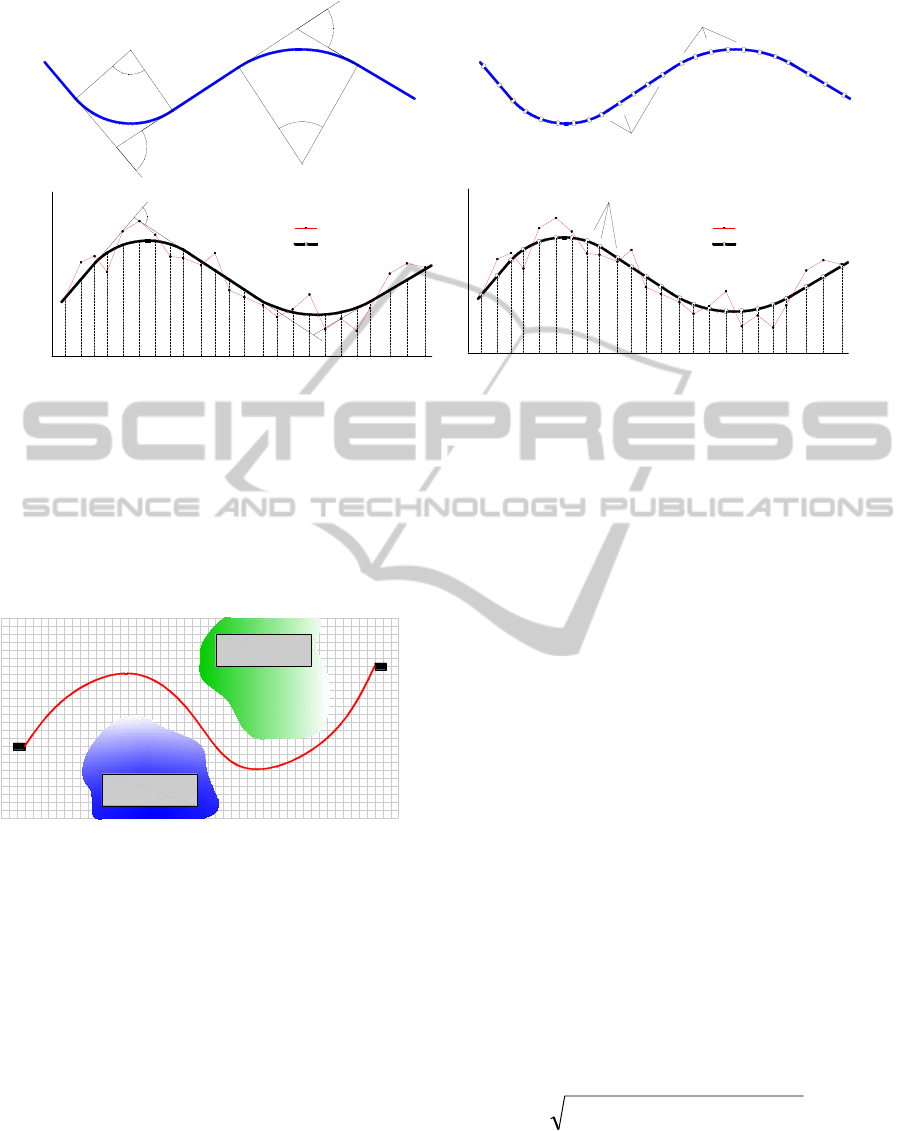
Figure 1: a & c) Horizontal and Vertical Alignment configuration with traditional method, b & d) Horizontal and Vertical

Alignment configuration using station points.

earthwork amount of cut and fill. For these purposes,

two different matrices are used for each set of data

to feed the model during the alignment development

process. Figure 2 shows a typical 2D format for a

study area:

Figure 2: Typical grid format (2D) of a study region.

2.2 The Model Cost Components

The goodness of any alignment is evaluated in terms

of cost. The lower the cost, the better will be the

solution. In general many costs could be included

and the optimum alignment should trade-off among

them. In this study, a three dimensional alignment is

modelled and tested upon few different cost

components which the experiments are based on.

These costs are related to:

1. Client or General Costs

• Length dependent cost (construction costs)

• Earthwork costs

• Location costs (environmental costs)

2. User Costs

• Fuel consumption costs

3. Geometric Design Costs

• Grade costs

• Horizontal curvature costs

• Vertical curvature costs

Other components are also possible for inclusion.

The following sections give some details for the

incorporated components.

2.2.1 Length Dependent Cost (C

Length

)

This cost directly affects the construction,

maintenance, and user costs and therefore it is

considered as one of the most influencing factors in

highway alignment optimization problems.

Highway alignment construction cost is a

function of its length. To calculate this cost, the

length of the alignment is multiplied by the unit

construction cost as:

Len

= L x Unit Construction Cost (1)

Where, L is the total length of the alignment. The

alignment length is a function of the x and y

coordinate of the station points (decision variables).

L =











)()(

iiii

YYXX

(1-1)

for all i = 0, 1, 2 … (n-1)

Where n is the total number of station points.

R 1

Deflection

Angle 1

PC 2

PT 2

PC 1

PT 1

HIP 1

R 2

R 1

Deflection

Angle 2

HIP 2

H Curve

Tangent

Station Points

( a ) ( b )

X Distances (Stations)

Elevations

VIP 1

g1 %

VIP 2

g2 %

g3 %

A = g2 - g1

NGE

Grade Line

Station Points

( c ) ( d )

Elevations

NGE

Grade Line

Start

End

High Unit Cost Area

(Sensitive Area

)

Proposed highway

alignment

High Unit Cost Area

(Sensitive Area)

A GENETIC ALGORITHM APPROACH TO A 3D HIGHWAY ALIGNMENT DEVELOPMENT

131

2.2.2 Location Dependent Cost (C

Location

)

This represents the costs of land acquisitions and

special requirements for construction at the locations

where the alignment passes through.

Location





xUCellCl

(2)

Where: C

Location

is the total alignment location cost;

is the length of the alignment located in a grid cell

(k) with a specific cost value; UCellC is the unit cell

cost of that cell; and p is the total number of cells

that the alignment passes through. Thus, (

∑











) where L is the length of the alignment.

2.2.3 User Costs (C

User

)

This cost represents the cost incurred by the users to

travel along the road. Here it is calculated by

multiplying the annual traffic volume (TV) by the

design life of the road (T) to give the total traffic

using the road. This in turn is multiplied by the unit

cost of the vehicle travelling unit length (UTC)

multiplied by the length of the alignment (L). Thus:

Use

= TV x T x UTC x L (3)

2.2.4 Earthwork Costs (C

)

This represents the cost of earthwork in terms of cut

and fill amount. An approximate method is used to

calculate the amount of cut and fill. The difference

in elevation between the grade line and natural

ground elevation for cut (h

) and fill (h

) is

calculated and directly multiplied by the length of

that section (l

), width of the road (w), and unit cost

of cut and/or fill. Thus:

l



x



h



orh











xwx



UFCorUCC



(4)

Where h

and h

is the average cut or fill depth

between station points (i+1) and (i) while l

is the

length of that section, and UFC or UCC is the unit

fill or cut cost.

2.2.5 Grade Violation Costs (G

Violation

)

This is a form of penalizing the solution and is

applied only when the grade of a segment between

two station points violates the maximum specified

grade. The difference in grade between the actual

calculated grade and the maximum grade is multi-

plied by a user defined cost factor.







G



xUDC





(5)

Where G

is the grade value between the points (i)

and (i-1) while UDC is the user defined cost factor.

2.2.6 Horizontal Curvature Violation Cost

(HC

Violation

)

Curvature of horizontal alignment is one of the

standard design requirements to ensure gradual

transition between two different directions safely at

the assigned design speed. The cost of violated

curvature according to chord definition at each

station point is considered as follow:



∑





HC





then:











HC





HC















(6)

Where HC

i_existing

is the existing curvature value at

point i, HC

i_allowable

is the allowable curvature at that

point, and CVC is the curvature violation cost.

2.3 The Fitness Function

In this paper, the costs above are combined linearly

to form the total cost (C

Total

) and the aim of the

process is therefore to minimize;

Total

= a1.C

Traffic

+ a2.C

Location

+ a3.C

Construction

a4.C

Earthwork

+ a5. G

Violation

+ a6. HC

Violation

(7)

Where; a1, a2, a3, a4, a5 and a6 are weighting

factors of the individual cost components.

Other combinations of fitness function could also be

used.

3 EXPERIMENTAL SETUP

3.1 Chromosome Representation

Using the ideas of station points introduced above,

the method defines alignment through generating

station points along the centre line of the alignment.

The x, y, and z coordinates of the station points are

considered as the decision variables of the alignment

ICEC 2010 - International Conference on Evolutionary Computation

132

The chromosome map is as shown in Figure 3. It

contains the three dimensional coordinates of each

station point. The station points appear in the order

in which they occur along the length of the

alignment.

Index (i) 0 1 2 … i … … n

Individual

(j)

Figure 3: Chromosome representation.

3.2 Initial Population Generation

An initial population of random individuals is

generated such that:

 All station points are within the study area.

min

≤ X

max

, Y

min

≤ Y

max

and Z

min

≤ Z

max

where i = 1, 2, … , n-1.

 The 3D components of each gene are encoded

using floating point numbers with single

precision.

 The first and last points (0 and n) are fixed as the

required terminal points.

 The station points are sorted in the order of their

X values (Xi ≤ Xi+1). This process is specific to

the initial population generation only.

3.3 Reproduction

3.3.1 Selection

In this study parents are selected according to their

fitness (based on ranking). The selected parents

undergo crossover and mutation to produce

offspring. The created offspring are then evaluated

by the fitness function. The fittest individuals are

merged into the population to breed in the next

generation while the bad solutions die off (Davis,

1991).

3.3.2 Crossover

In this paper a multiple random point crossover is

used to swap a segment or segments of genes

between two individuals to form two offspring. The

entire gene code (X, Y, and Z coordinates) within

the segments are swapped during this process.

3.3.3 Mutation

First, simple uniform mutation, as a standard GA

operator, is used to help the solution in evolving

over the successive generations. Different

parameters (e.g. number of individuals, number of

station points, mutation probability, number of

generations up to 100,000, and so on) have been

investigated. Moreover, different strategies have

been applied during the process. The strategies are

considered to be different mutation rates to select

different station points for mutation and dynamic

consideration of the study area. These strategies are

considered to test the level of effectiveness of the

applied method. None of these parameters and

strategies has produced a good solution.

Later, as an attempt to improve the effectiveness

of the mutation operator, the simple uniform

mutation is modified. This modified uniform

mutation (MUM) is based on that described by

Michalewicz (1999). It is adapted to associate a

number of station points with a single mutated one.

The trend of this mutation is to enhance the search,

reduce the messiness of the alignment configuration,

and to produce a smoother alignment. This operator,

as with simple uniform mutation, selects a gene

position (p) randomly and assigns a new random

value for its X, Y, and Z coordinates. Then the

operator generates two more locations (l

and l

)

provided that l

< p < l

. Then, all the genes (station

points) that locate between l

and p, and l

and p on

the other side are reallocated and put on a straight

line connecting the newly generated gene at (p) with

the selected genes at l

and l

4 EXPERIMENTAL RESULTS

4.1 Standard GA Tests

Figure 4 shows a typical result with simple uniform

mutation for a 2D highway alignment. A legend list

(Figure 5) is also provided to illustrate the land

feature configurations of the study region.

Figure 4: An alignment result for a horizontal highway

alignment using standard GA operators. (Land use grid

map).

A GENETIC ALGORITHM APPROACH TO A 3D HIGHWAY ALIGNMENT DEVELOPMENT

133

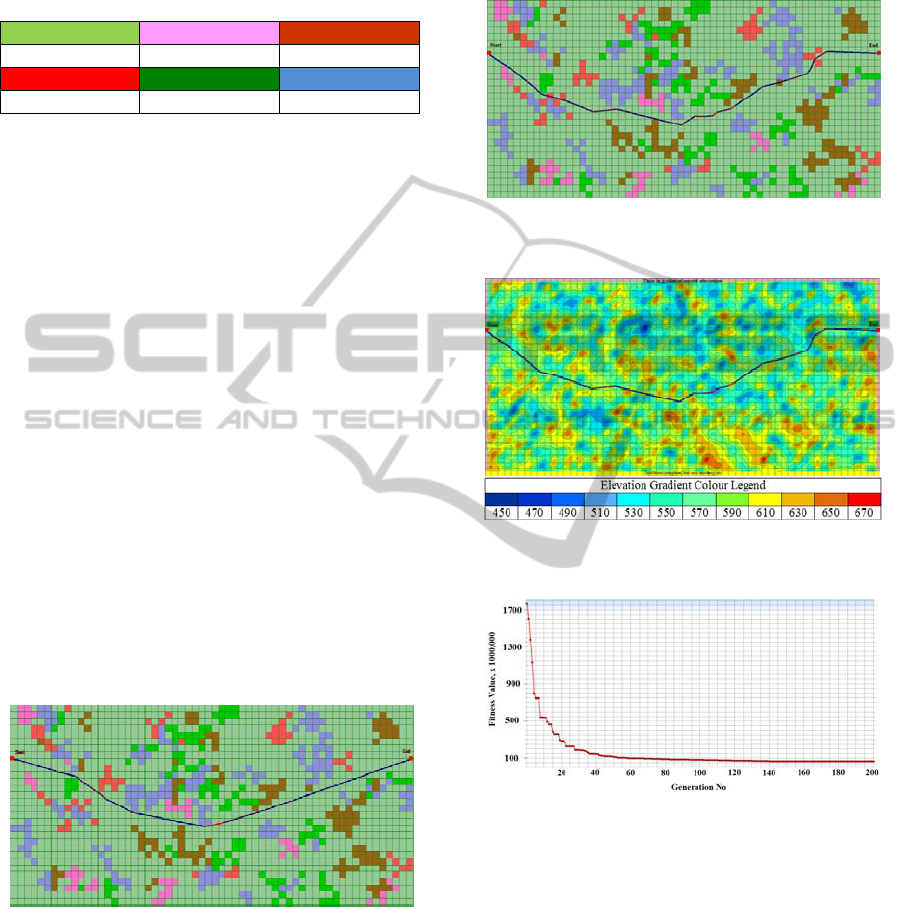
The result which obtained by this method was

not satisfactory even after 50,000 generations. The

fitness value of the final solution was 38,339,321

unit cost.

Low cost Moderate cost Normal cost

High cost Very high cost Most high cost

Figure 5: Cost colour legends of the land use grid maps.

4.2 Modified GA Tests

The modified GA formulation, which specified by

MUM as mentioned above, was also tested on a 2D

highway alignment as shown in Figure 6. The result

holds a fitness value 24,583,831 unit cost at

generation 1000. The resulting alignment is as

straight as possible, relatively smooth, and passes

through the low cost fields. The practicality of this

mutation was then tested on a 3D alignment as well.

The 3D result holds a fitness value 53,624,912 unit

cost at generation 2000. It worth to mention that this

operator, as for the 2D horizontal alignment, has the

following merits on the vertical profile:

a. It produces as low as possible earthwork costs.

b. It yields a relatively smooth alignment.

c. It tries to locate the alignment as close as possible

to the natural ground surface.

d. It tries to wind around the high and low elevation

locations to minimize cut and fill costs.

Typical results are shown in Figures 7 to 10.

Figure 6: Test result of a modified uniform mutation

(MUM) for a 2D alignment. (Land use grid map).

The two tests (2D and 3D) resulted in obtaining two

different horizontal alignment configurations

(Figures 6 & 7) due to the effect of the third

dimension (Z) on the final outcome. These

demonstrate that the horizontal and vertical

alignments are unlikely to be global optima unless

they are considered simultaneously. It should be

noted that the initial test was conducted without

considering the grade and curvature costs as they

need special techniques to handle them and these are

discussed in the succeeding sections.

Figure 7: Horizontal alignment test result of MUM for a

3D highway alignment. (Land use grid map).

Figure 8: Horizontal alignment result of MUM for a 3D

alignment on contour map.

Figure 9: Fitness graph. (Note: only the substantial

improvements over 200 generations are shown).

However, as is clear in the results, the modified

uniform mutation (MUM) method still keeps some

sharp bends (horizontally and vertically) throughout

the length of the alignment. These sharp bends are

expected from such a mutation method.

Furthermore, the vertical one possesses some

grades (upwards and downwards) which are greater

than the maximum permitted one. These alignment

criteria cannot be improved unless specific

algorithm techniques are developed and associated

with the search process. This needs to be considered

as constraints according to the geometric design and

safety requirements of the highway.

ICEC 2010 - International Conference on Evolutionary Computation

134

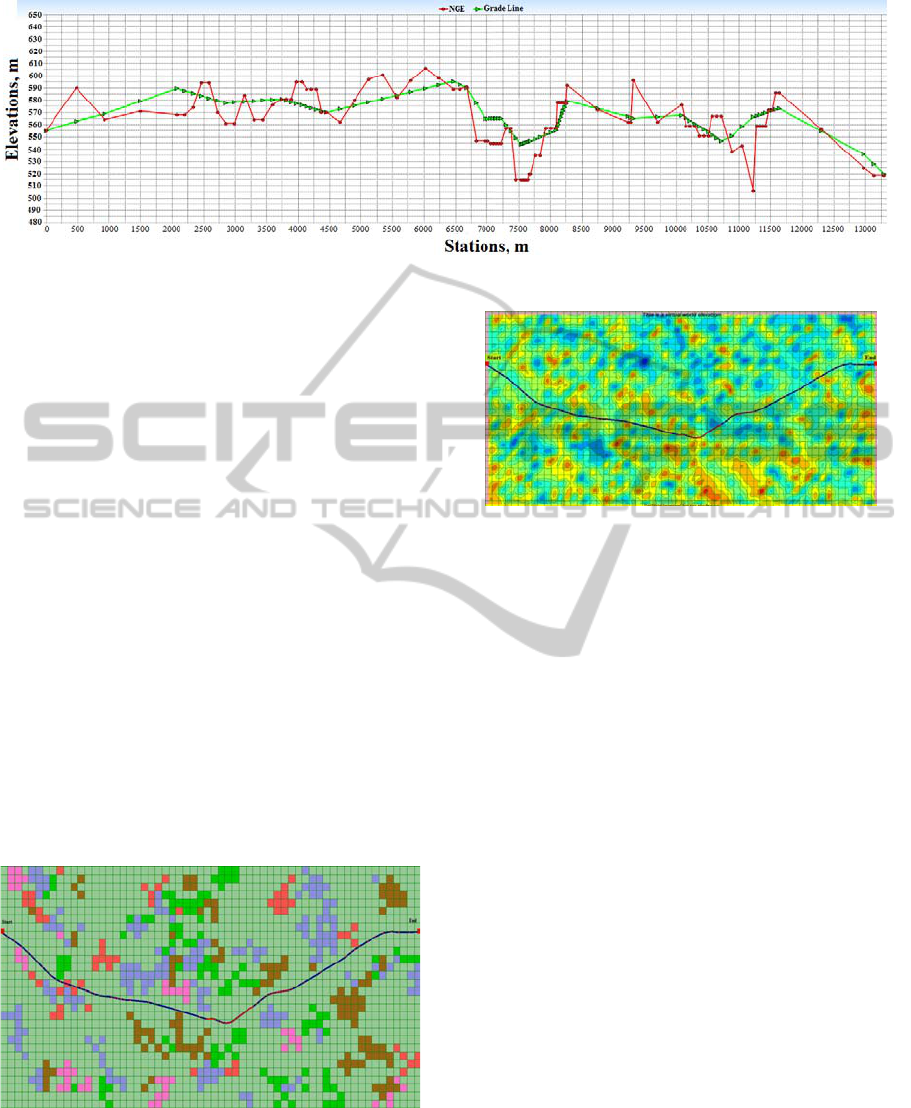
Figure 10: Vertical alignment profile result (grade line elevations) of MUM for a 3D highway alignment.

4.3 Grade and curvature Constraint

Handling Technique Tests

Three different algorithms are developed to handle

curvature for the horizontal alignment, curvature and

gradient for the vertical alignment. Penalty and

repair techniques are considered to look after the

point locations along the alignment that violate the

allowable horizontal curvature limits. Penalty is used

for maximum gradient violation while repair

technique is applied for vertical curvature violation.

The formulations of these techniques are based on

standard design requirements for both geometric

design and safety. These techniques are individually

applied to each single station point or location where

the violations exist.

Different experiments have been carried out to

test the effect of each technique separately and

simultaneously. The test results show that the

resulting solutions are improved significantly as

shown in Figure 11 to 13. The results show that the

solution is good with no or very few gradient and

curvature violations.

Figure 11: Horizontal alignment result for a 3D alignment

evolved with curvature and grading constraint handling.

(Land use grid map).

Figure 12: Horizontal alignment result for a 3D alignment

evolved with curvature and grading constraint handling.

(Contour map).

5 CONCLUSIONS

A three dimensional highway alignment

optimization model based on a genetic algorithm has

been developed. A new technique has been

introduced to define the alignment configuration.

Station points along the centre line of the alignment

have been used to generate alignments of different

configurations. Specific genetic algorithm operators

and constraint handling techniques were tested and

the results indicate that the method holds promises.

The results also show that the station point

technique is promising if it is assisted by constraint

handling algorithms to produce better solutions. It is

concluded that the constraint handling techniques

assisted in the improvement of the alignment

curvature characteristics and the reduction or

prohibition of the gradient violations.

However, the results show that further

developments and further investigations are required

to verify generating more realistic alignments. More

specific GA operators and further modifier and

constraint handling techniques will be investigated.

Moreover, the model needs to be tested on different

worlds and the model parameters need to be

determined and verified for applicability in real

world application problems.

A GENETIC ALGORITHM APPROACH TO A 3D HIGHWAY ALIGNMENT DEVELOPMENT

135

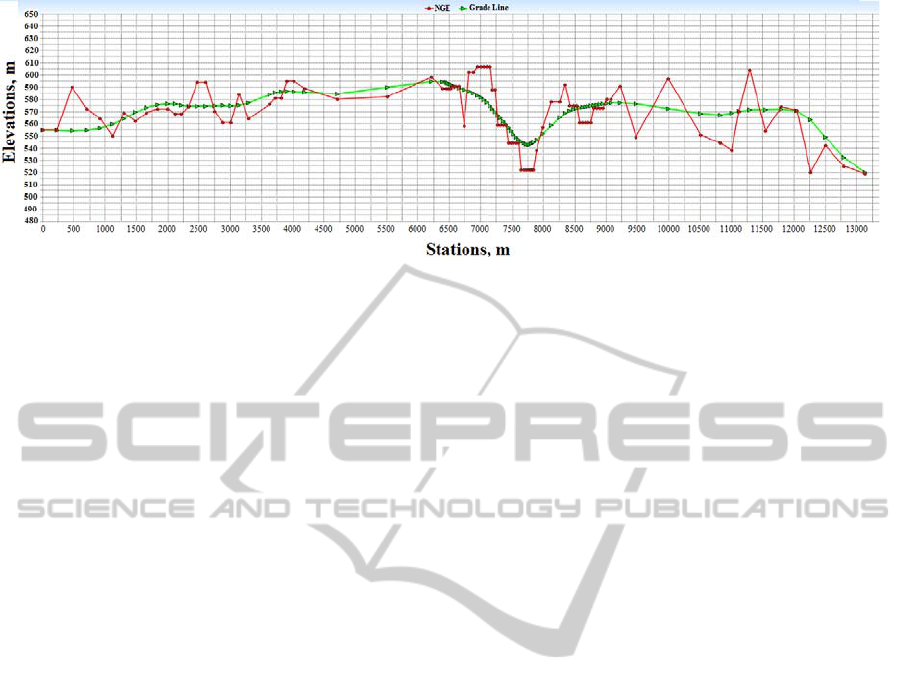
Figure 13: Vertical alignment profile for a 3D highway alignment evolved with curvature and grading constraint handling.

REFERENCES

American Association of State Highway and

Transportation Officials, 1994. USA.

Beasley, D., Bull, D. R., and Martin, R. R., 1993. An

Overview of Genetic Algorithms: Part 1

Fundamentals, University of Computing, 15(2), 58-69.

Chew, E. P., Goh, C. J., and Fwa, T. F., 1989.

Simultaneous Optimization of Horizontal and Vertical

Alignments of Highways, Transportation research,

Part B, 23(5), 315-329.

Davis, L., 1991. Handbook of Genetic Algorithms, Van

Nostrand Reinhold, New York, USA.

Design Manual for Roads and Bridges, (1992-2008). The

Highways Agency, UK.

Ford, M., 2007. A Genetic Algorithm Based Decision

Support System for the Sustainable Location of

development Allocations, Ph.D. Thesis, University of

Nottingham, UK.

Fwa, T. F., Chan, W. T. and Sim, Y. P., 2002. Optimal

Vertical Alignment Analysis for Highway Design,

Journal of Transportation Engineering, Vol. 128, No.

5, pp. 395 – 402.

Jha, M. K. and Schonfeld, P., 2000. Integrating Genetic

Algorithms and Geographic Information System to

Optimize Highway Alignments, Transportation

Research Record, 1719, 233-240.

Jong, J. C., 1998. Optimizing Highway Alignments with

Genetic Algorithms, Ph.D. dissertation, University of

Maryland, College Park, USA.

Jong, J. C. and Schonfeld, P., 1999. Cost Functions for

Optimizing Highway Alignments, Transportation Re-

search Record, 1659, 58-67.

Maji, A. and Jha, M. K., 2009. Multi-Objective Highway

Alignment Optimization Using A Genetic Algorithm,

Journal of Advanced Transportation, 43 (4), 481-504.

Mathews, K. B., Craws, S., Mackenzie, I., Elder, S. and

Sibbald, A. R., 1999. Applying Genetic Algorithms to

Land Use Planning. In: Proceedings of the 18

Workshop of the UK Planning and Scheduling Spatial

Interest Group, 1999, University of Salford, UK.

Mawdesley, M. J., AL-Jibouri, S. H. & Yang, H., 2002.

Genetic Algorithms for Construction Site Layout in

Project Planning, Journal of Construction Engineering

and Management, 128 (5), 418-426.

Michalewicz, Z., 1999. Genetic Algorithms + Data

Structures = Evolution Programs, Springer-Verlag,

USA.

Mitchell, M., 1996. An Introduction to Genetic

Algorithms, The MIT Press, USA.

Shaw, J. F. B. and Howard, B. E., 1982. Expressway

Route Optimization by OCP, Journal of

Transportation Engineering, ASCE, 108(3), 227-243.

Tat, C. W. & Tao, F., 2003. Using GIS and Genetic

Algorithms in Highway Alignment Optimization,

Intelligent Transportation System, 2, 1563-1567.

Wright, P. H. & Ashford, N. J., 1998. Transportation

Engineering: Planning and Design, John Wiley and

Sons, USA.

ICEC 2010 - International Conference on Evolutionary Computation

136