
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY
LOG ANONYMIZATION
Amin Milani Fard and Ke Wang
School of Computing Science, Simon Fraser University, BC, V5A 1S6, Burnaby, Canada
Keywords: Query Logs Data, Privacy-preserving Data Publishing, Transaction Data Anonymization, Item
Generalization.
Abstract: Web query log data contain information useful to research; however, release of such data can re-identify the
search engine users issuing the queries. These privacy concerns go far beyond removing explicitly
identifying information such as name and address, since non-identifying personal data can be combined
with publicly available information to pinpoint to an individual. In this work we model web query logs as
unstructured transaction data and present a novel transaction anonymization technique based on clustering
and generalization techniques to achieve the k-anonymity privacy. We conduct extensive experiments on the
AOL query log data. Our results show that this method results in a higher data utility compared to the state-
of-the-art transaction anonymization methods.
1 INTRODUCTION
Web search engines generally store query logs data
for the purpose of improving ranking algorithms,
query refinement, user modelling, fraud/abuse
detection, language-based applications, and sharing
data for academic research or commercial needs
(Cooper, 2008). On the other hand, the release of
query logs data can seriously breach the privacy of
search engine users. The privacy concern goes far
beyond just removing the identifying information
from a query. Sweeney (Sweeney, 2000) showed
that even non-identifying personal data can be
combined with publicly available information, such
as census or voter registration databases, to pinpoint
to an individual. In 2006 the America Online (AOL)
query logs data, over a period of three months, was
released to the public (Barbaro et al., 2006).
Although all explicit identifiers of searchers have
been removed, by examining query terms, the
searcher No. 4417749 was traced back to the 62-
year-old widow Thelma Arnold. Since this scandal,
data publishers become reluctant to provide
researchers with public anonymized query logs
(Hafner, 2006).
An important research problem is how to render
web query log data in such a way that it is difficult
to link a query to a specific individual while the data
is still useful to data analysis. Several recent works
start to examine this problem, with (Kumar et al.,
2007) and (Adar, 2007) from web community
focusing on privacy attacks, and (He et al., 2009),
(Terrovitis et al., 2008), and (Xu et al., 2008) from
the database community focusing on anonymization
techniques. Although good progresses are made, a
major challenge is reducing the significant
information loss of the anonymized data.
The subject of this paper falls into the field of
privacy preserving data publishing (PPDP) (Fung et
al., 2010), which is different from access control and
authentication associated with computer security.
The work in these latter areas ensures that the
recipient of information has the authority to receive
that information. While such protections can
safeguard against direct disclosures, they do not
address disclosures based on inferences that can be
drawn from released data. The subject of PPDP is
not much on whether the recipient can access to the
information or not, but is more on what values will
constitute the information the recipient will receive
so that the privacy of record owners is protected.
1.1 Motivations
This paper studies the query log anonymization
problem with the focus on reducing information
loss. One approach is modelling query logs data as a
special case of transaction data, where each
109
Milani Fard A. and Wang K. (2010).
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY LOG ANONYMIZATION.
In Proceedings of the International Conference on Security and Cryptography, pages 109-119
DOI: 10.5220/0002924901090119
Copyright
c
SciTePress

transaction contains several “items” from an item
universe I. In the case of query logs, each transaction
represents a query and each item represents a query
term. Other examples of transaction data are emails,
online clicking streams, online shopping
transactions, and so on. As pointed out in (Terrovitis
et al., 2008) and (Xu et al., 2008), for transaction
data, the item universe I is very large (say thousands
of items) and a transaction contains only a few
items. For example, each query contains a tiny
fraction of all query terms that may occur in a query
log. If each item is treated as a binary attribute with
1/0 values, the transaction data is extremely high
dimensional and sparse. On such data, traditional
techniques suffer from extreme information loss
(Terrovitis et al., 2008) and (Xu et al., 2008).
Recently, the authors of (He et al., 2009) adapted
the top-down Mondrian (LeFevre et al., 2006)
partition algorithm originally proposed for relational
data to generalize the set-valued transaction data.
We refer to this algorithm as Partition in this paper.
They adapted the traditional k-anonymity (Samarati,
2001) and (Sweeney, 2002) to the set valued
transaction data. A transaction database is k-
anonymous if transactions are partitioned into
equivalence classes of size at least k, where all
transactions in the same equivalence class are
exactly identical. This notion prevents linking
attacks in the sense that the probability of linking an
individual to a specific transaction is no more than
1/k.
Our insight is that Partition method suffers from
significant information loss on transaction data.
Consider the transaction data S={ t
1
, t
2
, t
3
, t
4
, t
5
} in
the second column of Table 1 and the item
taxonomy in Figure 1. Assume k = 2. Partition
works as follows. Initially, there is one partition
P
{food}
in which the items in every transaction are
generalized to the top-most item food. At this point,
the possible drill-down is food {fruit, meat,
dairy}, yielding 2
3
-1 sub-partitions corresponding to
the non-empty subsets of {fruit, meat, dairy}, i.e.,
P
{fruit}
, P
{meat}
, ..., and P
{fruit,meat,dairy}
, where the curly
bracket of each sub-partition contains the common
items for all the transactions in that sub-partition.
All transactions in P
{food}
are then partitioned into
these sub-partitions. All sub-partitions except
P
{
fruit,meat
}
violate k-anonymity (for k=2) and thus are
merged into one partition P
{food}
. Further partitioning
of P
{
fruit,meat
}
also violates k-anonymity. Therefore, the
algorithm stops with the result shown in the last
column of Table 1.
One drawback of Partition is that it stops
partitioning the data at a high level of the item
taxonomy. Indeed, specializing an item with n
children will generate 2
n
-1 possible sub-partitions.
This exponential branching, even for a small value
of n, quickly diminishes the size of a sub-partition
and causes violation of k-anonymity. This is
especially true for query logs data where query
terms are drawn from a large universe and are from
a diverse section of the taxonomy.
Figure 1: Food taxonomy tree.
Table 1: The motivating example and its 2-anonymization.
TID Original Data Partition
t
1
<orange, chicken, beef> <fruit, meat>
t
2
<banana, beef, cheese> <food>
t
3
<chicken, milk, butter> <food>
t
4
<apple, chicken> <fruit, meat>
t
5
<chicken, beef> <food>
Moreover, the Partition does not deal with item
duplication. As an example, the generalized t
3
in the
third column of Table 1 contains only one
occurrence of food, which clearly has more
information loss than the generalized transaction
<food, food, food> because the latter tells more
truthfully that the original transaction purchases at
least three items. Indeed, the TFIDF used by many
ranking algorithms critically depends on the term
frequency of a term in a query or document.
Preserving the occurrences of items (as much as
possible) would enable a wide range of data analysis
and applications.
1.2 Contributions
To render the input transaction data k-anonymous,
our observation is: if “similar” transactions are
grouped together, less generalization and
suppression will be needed to render them identical.
As an example, grouping two transactions <Apple>
and <Milk> (each having only one item) entails
more information loss than grouping two
transactions <Apple> and <Orange>, because the
former results in the more generalized transaction
<Food> whereas the latter results in the less
generalized transaction <Fruit>. Therefore, with a
proper notion of transaction similarity, we can treat
the transaction anonymization as a clustering
problem such that each cluster must contain at least
SECRYPT 2010 - International Conference on Security and Cryptography
110

k transactions and these transactions should be
“similar”. Our main contributions are as follows:
Contribution 1. For a given item taxonomy, we
introduce the notion of the Least Common
Generalization (LCG) as the generalized
representation of a subset of transactions, and as a
way to measure the similarity of a subset of
transactions. The distortion of LCG models the
information loss caused by both item generalization
and item suppression. We devise a linear-time
algorithm to compute LCG.
Contribution 2. We formulate the transaction
anonymization as the problem of clustering a given
set of transactions into clusters of size at least k such
that the sum of LCG distortion of all clusters is
minimized.
Contribution 3. We present a heuristic linear-time
solution to the transaction anonymization problem.
Contribution 4. We evaluate our method on the
AOL query logs data.
The structure of the paper is as follows. Section 2
describes problem statements. Section 3 gives our
clustering algorithm. Section 4 presents the detailed
algorithm for computing LCG. Section 5 presents
the experimental results. Section 6 reviews related
works. We conclude in Section 7.
2 PROBLEM STATEMENTS
This section defines our problems. We use the terms
“transaction” and “item”. In the context of web
query logs, a transaction corresponds to a query and
an item corresponds to a query term.
2.1 Item Generalization
We assume that there is a taxonomy tree T over the
item universe I, with the parent being more general
than all children. This assumption was made in the
literature (Samarati, 2001), (Sweeney, 2002), (He et
al., 2009), (Terrovitis et al., 2008). For example,
WordNet (Fellbaum, 1998) could be a source to
obtain the item taxonomy.
The process of generalization refers to replacing
a special item with a more general item (i.e., an
ancestor), and the process of specialization refers to
the exact reverse operation. In this work, an item is
its own ancestor and descendant.
Definition 1 (Transactions and Generalization). A
transaction is a bag of items from I (thus allowing
duplicate items). A transaction t’ is a Generalized
Transaction of a transaction t, if for every item i’t’
there exists one distinct item it such that i’ is an
ancestor of i. In this case, t is the Specialized
Transaction of t’.
The above transaction model is different from
(He et al., 2009) in several ways. First, it allows
duplicate items in a transaction. Second, it allows
items in a transaction to be on the same path in the
item taxonomy, in which case, each item represents
a distinct leaf item. For example, we interpret the
transaction <Fruit, Food> as: Fruit represents (the
generalization of) a leaf item under Fruit and Food
represents a leaf item under Food that is not
represented by Fruit. Also, if t’ is a generalized
transaction of t, each item i’t’ represents one
distinct item it. We say that an item it
is
suppressed in t’ if no i’t’ represents the item i.
Hence, our generalization also models item
suppression.
Example 1: Consider the taxonomy tree in Figure 1
and the transaction t=<Orange, Beef>. All possible
generalized transactions of t are <>, <Orange>,
<Beef>, <Orange, Beef>, <Fruit, Beef>, <Orange,
Meat>, <Fruit, Meat>, <Fruit>, <Meat>, <Food>,
<Orange, Food>, <Food, Beef>, <Fruit, Food>,
<Food, Meat>, and <Food, Food>. For t’=<Fruit>,
Fruit represents (the generalization) of some item
under the category Fruit (i.e., Orange), and Beef is a
suppressed item since no more item in t’ represents
it. For t’=<Food>, Food represents one item under
Food, therefore, one of Orange and
Beef in t is
suppressed. For t’=<Food, Food>, each occurrence
of Food represents a different item in t.
2.2 Least Common Generalization
The main idea of transaction anonymization is to
build groups of identical transactions through
generalization. We introduce the following notion to
capture such generalizations.
Definition 2 (LCG). The Least Common
Generalization of a set of transactions S, denoted by
LCG(S), is a common generalized transaction for all
of the transactions in S, and there is no other more
special common generalized transaction.
The following properties follow from the above
definition. The proof has been omitted due to the
space limit
Property 1 LCG(S) is unique for a given S.
Property 2 The length of LCG(S) (i.e. the number of
items in it) is equal to the length of the shortest
transaction in S. This property can be ensured by
padding the root item to LCG if necessary.
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY LOG ANONYMIZATION
111

Example 2: Consider the taxonomy tree in Figure 1.
Let S
1
= {<Orange, Beef>, <Apple, Chicken, Beef>},
LCG(S
1
) = <Fruit, Beef>. LCG(S
1
) cannot be <Fruit,
Meat> since <Fruit, Beef> is a more specialized
common transaction. For S
2
= {<Orange, Milk>,
<Apple, Cheese, Butter>}, LCG(S
2
)=<Fruit, Dairy>.
Dairy represents Milk in the first transaction and
represents one of Cheese and Butter in the second
transaction. Thus one of Cheese or Butter is
considered as a suppressed item. For S
3
= {<Orange,
Apple>, <Orange, Banana, Milk>, <Banana, Apple,
Beef>}, LCG(S
3
)=<Fruit, Fruit>, which represents
that all three transactions contain at least two items
under Fruit. Milk and Beef are suppressed items. For
S
4
= {<Orange, Beef>, <Apple, Milk>}, LCG(S
4
) =
<Fruit, Food>, where Food represents Beef in the
first transaction and Milk in the second transaction.
Here LCG contains both a parent and a child item.
Various metrics have been proposed in the
literature to measure the quality of generalized data
including Classification Metric (CM), Generalized
Loss Metric (LM) (Iyengar, 2002), and Discernibility
Metric (DM) (Bayardo et al., 2005). We use LM to
measure item generalization distortion. The similar
notion of NCP has also been employed for set-
valued data (Terrovitis et al., 2008) and (He et al.,
2009). Let M be the total number of leaf nodes in the
taxonomy tree T, and let Mp be the number of leaf
nodes in the subtree rooted at a node p. The Loss
Metric for an item p, denoted by LM(p), is defined
as (Mp-1) / (M-1). For the root item p, LM(p) is 1. In
words, LM captures the degree of generalization of
an item by the percentage of the leaf items in the
domain that are indistinguishable from it after the
generalization. For example, considering taxonomy
in Figure 1, LM(Fruit)=2/7.
Suppose that we generalize every transaction in a
subset of transactions S to a common generalized
transaction t, and we want to measure the distortion
of this generalization. Recall that every item in t
represents one distinct item in each transaction in S
(Definition 1). Therefore, each item in t generalizes
exactly |S
| items, one from each transaction in S,
where |S| is the number of transactions in S. The
remaining items in a transaction (that are not
generalized by any item in t) are suppressed items.
Therefore, the distortion of this generalization is the
sum of the distortion for generalized items, |S|Σ
it
LM(i), and the distortion for suppressed items. For
each suppressed item, we charge the same distortion
as if it is generalized to the root item, i.e., 1.
Definition 3 (GGD). Suppose that we generalize
every transaction in a set of transactions S to a
common generalized transaction t. The Group
Generalization Distortion of the generalization is
defined as GGD(S, t) = |S|Σ
it
LM(i) + N
s
, where N
s
is the number of occurrences of suppressed items.
To minimize the distortion, we shall generalize S
to the least common generalization LCG(S), which
has the distortion GGD(S, LCG(S)).
Example 3: Consider the taxonomy in Figure 1 and
S
1
={<Orange, Beef>, <Apple, Chicken, Beef>}. We
have LCG(S
1
) = <Fruit, Beef>. LM(Fruit)=2/7,
LM(Beef)=0, and |S
1
|=2. Since Chicken is the only
suppressed item, N
s
=1. Thus GGD(S
1
, LCG(S
1
)) =
2(2/7+0) + 1 = 11/7.
2.3 Problem Definition
We adopt the transactional k-anonymity in (He et al.,
2009) as our privacy notion. A transaction database
D is k-anonymous if for every transaction in D, there
are at least k-1 other identical transactions in D.
Therefore, for a k-anonymous D, if one transaction
is linked to an individual, so are at least k-1 other
transactions, so the adversary has at most 1/k
probability to link a specific transaction to the
individual. For example, the last column in Table 1
is a 2-anonymous transaction database.
Definition 5 (Transaction Anonymization). Given a
transaction database D, a taxonomy of items, and a
privacy parameter k, we want to find the clustering
C={S
1
,…,S
n
} of D such that S
1
,…,S
n
are pair-wise
disjoint subsets of D with each S
i
containing at least
k transactions from D, and Σ
i=1..|C|
GGD(S
i
, LCG(S
i
))
is minimized.
Let C={S
1
,…,S
n
} be a solution to the above
anonymization problem. A k-anonymized database
of D can be obtained by generalizing every
transaction in S
i
to LCG(S
i
), i=1,…,n.
3 CLUSTERING APPROACH
In this section we present our algorithm Clump for
solving the problem defined in Definition 5. In
general, the problem of finding optimal k-
anonymization is NP-hard for k3 (Meyerson et al.,
2004). Thus, we focus on an efficient heuristic
solution to this problem and evaluate its
effectiveness empirically. In this section, we assume
that the functions LCG(S) and GGD(S, LCG(S)) are
given. We will discuss the detail of computing these
functions in Section 4.
The central idea of our algorithm is to group
transactions in order to reduce GGD(S
i
, LCG(S
i
)),
subject to the constraint that S
i
contains at least k
SECRYPT 2010 - International Conference on Security and Cryptography
112

transactions. Recall GGD(S, LCG(S)) = |S|Σ
iLCG(S)
LM(i) + N
s
and from Property 2, LCG(S) has the
length equal to the minimum length of transactions
in S. All “extra” items in a transaction that do not
have a generalization in LCG(S) are suppressed and
contributes to the suppression distortion N
s
. Since
the distortion of generalizing an item is no more than
the distortion of suppressing an item, one heuristic is
to group transactions of similar length into one
cluster in order to minimize the suppression
distortion N
s
.
Based on this idea, we present our algorithm
Clump. Let D be the input transaction database and
let n=|D|/k be the number of clusters, where |D|
denotes the number of transactions in D:
Step 1 (line 2-5): We arrange the transactions in D
in the decreasing order of the transaction length, and
we initialize the i
th
cluster S
i
, i=1,…,n, with the
transaction at the position (i-1)k+1 in the ordered
list. Since earlier transactions in the arranged order
have longer length, earlier clusters in this order tend
to contain longer transactions.
For the comparison purpose, we also implement
other transaction assignment orders, such as random
assignment order and the increasing transaction
length order (i.e., the exact reverse order of the
above algorithm). Our experiments found that the
decreasing order by transaction length produced
better results.
Step 2 (line 6-12): For each remaining transaction t
i
in the arranged order, we assign t
i
to the cluster S
j
such that |S
j
|<k and GGD(S
j
{t
i
}, LCG(S
j
{t
i
})) is
minimized. Since this step requires computing
GGD(S
j
{t
i
}, LCG(S
j
{t
i
})), we can restrict the
search to the first r clusters S
j
with |S
j
|<k, where r is
a pruning parameter. Our order of examining
transactions implies that longer transactions tend to
be assigned to earlier clusters.
Step 3 (line 13-17): after all of the n clusters contain
k number of transactions, for each remaining
transaction t
i
in the sorted order, we assign it to the
cluster S
j
with the minimum GGD(S
j
{t
i
},
LCG(S
j
{t
i
})).
Algorithm 1: Clump: Transaction Clustering.
Input: Transaction database: D, Taxonomy: T, Anonymity
parameter: k, n=|D|/k
Output: k-anonymous transaction database: D*
Method:
1. Initialize S
i
for i=1,...,|D|;
2. Sort the transactions in D in the descending order of
length
3. for i = 1 to n do
4. assign the transaction at the position (i-1)k+1 to S
i
5. end for
6. while |S
j
|<k for some S
j
do
7. for each unassigned transaction t
i
in sorted order do
8. Let S
j
be the cluster such that |S
j
|<k and
GGD(S
j
{t
i
},LCG(S
j
{t
i
})) is minimized
9. LCG(S
j
) LCG(S
j
{t
i
})
10. S
j
S
j
{t
i
}
11. end for
12. end while
13. for each unassigned transaction t
i
do
14. Let S
j
be the cluster such that |S
j
|<k and
GGD(S
j
{t
i
},LCG(S
j
{t
i
})) is minimized
15. LCG(S
j
) LCG(S
j
{t
i
})
16. S
j
S
j
{t
i
}
17. end for
18. return LCG(S
i
) and S
i
, i=1,..., n
The major work of the algorithm is computing
GGD(S
j
{t
i
}, LCG(S
j
{t
i
})), which requires the
LCG(S
j
{t
i
}). We will present an algorithm for
computing LCG(S
i
) in time O(|T||S
i
|) in the next
section, where |T| is the size of the taxonomy tree T
and |S
i
| is the number of transactions in S
i
. It is
important to note that each cluster S
i
has a size at
most 2k. Since k is small, LCG can be computed
efficiently. In fact, the next lemma says that
LCG(S
j
{t
i
}) can be computed incrementally from
LCG(S
j
).
Lemma 1. Let t be a transaction, S be a subset of
transactions, and S’={LCG(S),t} consist of two
transactions. Then LCG(S{t}) =LCG(S’).
Proof: Omitted due to the space limit.
In words, the lemma says that the LCG of S
j
{t
i
}
is equal to the LCG of two transactions, LCG(S) and
t
i
. Thus if we maintain LCG(S
j
) for each cluster S
j
,
the computation of LCG(S
j
{t}) involves only two
transactions and takes the time O(|T|).
Theorem 1. For a database D and a taxonomy tree
T, Algorithm 1 runs in time O(|D|r|T|), where r is
the pruning parameter used by the algorithm.
Proof: We apply Counting Sort which takes O(|D|)
time to sort all transactions in D by their length.
Subsequently, the algorithm examines each
transaction once to insert it to a cluster. To insert a
transaction t
i
, the algorithm examines r clusters and,
for each cluster S
j
, it computes LCG(S
j
{t
i
}) and
GGD(S
j
{t
i
}, LCG(S
j
{t
i
})), which takes O(|T||S
j
|)
according to Theorem 2 in Section 4, where |S
j
| is
the number of transactions in S
j
. With the
incremental computing of LCG(S
j
{t
i
}) in Lemma
1, computing LCG(S
j
{t
i
}) takes time proportional
to |T|. Overall, the algorithm is in O(|D|r|T|).
Since |T| and r are constants, the algorithm takes
a linear time in the database size |D|.
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY LOG ANONYMIZATION
113

4 COMPUTING LCG
In the previous section, we make use of the
functions LCG(S) and GGD(S, LCG(S)) to determine
the cluster for a transaction. Since these functions
are frequently called, an efficient implementation is
crucial. In this section, we present a linear time
algorithm for computing LCG and GGD. We focus
on LCG because computing GGD is straightforward
once LCG is found.
4.1 Bottom-up Generalization
We present a bottom-up item generalization (BUIG)
algorithm to build LCG(S) for a set S of transactions.
First, we initialize LCG(S) with the empty set of
items. Then, we examine the items in the taxonomy
tree T in the bottom-up fashion: examine a parent
only after examining all its children. For the current
item i examined, if i is an ancestor of some item in
every transaction in S, we add i to LCG(S). In this
case, i is the least common generalization of these
items. If i is not an ancestor of any item in some
transaction in S, we need to examine the parent of i.
This algorithm is described in Algorithm 2. Let
S= <t
1
,…,t
m
>. For an item i, we use an array R
i
[1..m]
to store the number of items in a transaction of
which i is an ancestor. Specifically, R
i
[j] is set to the
number of items in the transaction t
j
of which i is an
ancestor. MinCount(R
i
) returns the minimum entry
in R
i
, i.e., min
j=1..m
R
i
[j]. If MinCount(R
i
)>0, i is an
ancestor of at least MinCount(R
i
) distinct items in
every transaction in S, so we will add MinCount(R
i
)
copies of the item i to LCG(S).
Algorithm 2 is a call to the recursive procedure
BUIG(root) with the root of T. Line 1-6 in the main
procedure initializes LCG and R
i
. Consider BUIG(i)
for an item i. If i is a leaf in T, it returns. Otherwise,
line 4-9 examines recursively the children i’ of i, by
the call BUIG(i’). On return from BUIG(i’), if
MinCount(R
i’
)>0, i’ is an ancestor of at least
MinCount(R
i’
) items in every transaction in S, so
MinCount(R
i’
) copies of i’ are added to LCG. If
MinCount(R
i’
)=0, i’ does not represent any item for
some transaction in S, so the examination moves up
to the parent item i; in this case, line 8 computes R
i
by aggregating R
i’
for all child items i’ such that
MinCount(R
i’
)=0. Note that, by not aggregating R
i’
with MinCount(R
i’
)>0, we stop generalizing such
child items. If i is the root, line 10-11 adds
MinTranSize(S)-|LCG| copies of the root item to
LCG, where MinTranSize(S) returns the minimum
transaction length of S. This step ensures that LCG
has the same length as the minimum transaction
length of S (Property 2).
Example 4: Let S={<Orange, Apple>, <Orange,
Banana, Milk>, <Banana, Apple, Beef>} and
consider the taxonomy in Figure 1. BUIG(Food)
recurs until reaching leaf items. Then the processing
proceeds bottom-up as depicted in Figure 2. Next to
each item i, we show o:R
i
, where o is the sequence
order in which i is examined and R
i
stores the
number of items in each transaction of which i is an
ancestor.
The first three items examined are Apple,
Orange, and Banana. R
Apple
= [1,0,1] (since Apple
appeared in transactions 1 and 3), R
Orange
= [1,1,0],
and R
Banana
= [0,1,1]. MinCount(R
i
)=0 for these
items i. Next, the parent Fruit is examined and
R
Fruit
= R
Apple
+ R
Orange
+ R
Banana
=[2,2,2]. With
MinCount(R
Fruit
) = 2, two copies of Fruit are added
to LCG, i.e., LCG(S)=<Fruit, Fruit> and we stop
generalizing Fruit.
A similar processing applies to the sub-trees at
Meat and Dairy, but no item i is added to LCG
because MinCount(R
i
)=0. Finally, at the root Food,
R
Food
= R
Meat
+ R
Dairy
= [0,1,1]. Note that we do not
add R
Fruit
because MinCount(R
Fruit
)>2, which signals
that the generalization has stopped at Fruit. Since
|LCG|=MinTranSize(S), no Food is added to LCG.
So the final LCG(S)=<Fruit, Fruit>. As mentioned
in Example 2, the two occurrences of Fruit indicate
that all three transactions contain at least two items
under Fruit.
Figure 2: BUIG’s processing order.
Algorithm 2: Bottom-up Item Generalization.
Input: Taxonomy: T, Set of m transactions: S = <t
1,
..., t
m
>
Output: LCG(S)
Method:
1. LCG ;
2. for each item iT do
3. for each t
j
S do
4. if t
j
contains i then R
i
[j] 1 else R
i
[j] 0
5. end for
6. end for
7. BUIG(root);
8. return LCG;
****
BUIG(i):
1. if i is a leaf in T then
2. return
SECRYPT 2010 - International Conference on Security and Cryptography
114

3. else
4. for each child i’ of i do
5. BUIG(i’);
6. if MinCount(R
i’
)>0 then
7. Add MinCount(R
i’
) copies of i’ to LCG
8. else R
i
R
i
+R
i’
/* examining the parent i */
9. end for
10. if i=root then
11. Add MinTranSize(S)-|LCG| copies of root to LCG
12. return
Theorem 2. Given a set of transactions S and a
taxonomy tree T of items, BUIG produces LCG(S)
and takes time O(|T||S|), where |S| is the number of
transactions in S and |T| is the number of items in
taxonomy tree T.
Proof: First, BUIG generalizes transactions by
examining the items in T in the bottom-up order and
stops generalization whenever encountering an item
that is a common ancestor of some unrepresented
item in every transaction in S. This property ensures
that each item added to LCD is the earliest possible
common ancestor of some unrepresented item in
every transaction. Second, BUIG visits each node in
T once, and at each node i, it examines the structures
R
i’
and R
j
of size |S|, where i’ is a child of i. So the
complexity is O(|T||S|).
4.2 A Complete Example
Let us illustrate the complete run of Clump using the
motivating example in Section 1.1. We reproduce
the five transactions t
1
to t
5
in Table 2, arranged by
the descending order of transaction length. Let k=2.
First, the number of clusters is m = 5/2 = 2, and the
first cluster S
1
is initialized to the first transaction t
1
and the second cluster S
2
is initialized to the third
transaction t
3
. Next, we assign the remaining
transactions t
2
, t
4
, and t
5
in that order. Consider t
2
. If
we assign t
2
to S
1
, LCG(S
1
{t
2
})={fruit,beef,food},
and GGD = 2(2/7+0+1) = 2.57. If we assign t
2
to
S
2
, LCG(S
2
{t
2
})={meat,dairy,food} and GGD =
2(1/7+2/7+1) = 2.85. Thus the decision is assigning
t
2
to S
1
resulting in S
1
={t
1
,t
2
} and LCG(S
1
)={fruit,
beef, food}.
Next, we assign t
4
to S
2
because S
1
has contained
k=2 transactions. So S
2
={t
3
, t
4
} and LCG(S
2
)=
<chicken,food>. Next, we have the choice of
assigning t
5
to S
1
or S
2
because both have contained
2 transactions. The decision is assigning t
5
to S
2
because it results in a smaller GGD, and LCG(S
2
)=
<chicken,food>. So the final clustering is S
1
={t
1
, t
2
}
and S
2
={t
3
, t
4
, t
5
}. The last column of Table 2 shows
the final generalized transactions.
Let us compare this result of Clump with the
result of Partition in the third column (which has
been derived in Section 1.1). For Clump, we
measure the distortion by ΣGGD(S
i
, LCG(S
i
)) over
all clusters S
i
. For Partition, we measure the
distortion by ΣGGD(S
i
, t
j
) over all sub-partitions S
i
where t
j
is the generalized transaction for S
i
. The
GGD for Clump is 2(2/7+0+1) + [3(0+1)+1] =
6.57, compared to [2(2/7+1/7)+1] + [3(1)+5] =
8.85 for the Partition.
Table 2: The motivating example and its 2-anonymization.
ID Original Data Partition Clump
T
1
<orange,chicken,beef> <fruit,meat> <fruit,beef,food>
T
2
<banana,beef,cheese> <food> <fruit,beef,food>
T
3
<chicken,milk,butter> <food> <chicken,food>
T
4
<apple,chicken> <fruit,meat> <chicken,food>
T
5
<chicken,beef> <food> <chicken,food>
5 EXPERIMENTS
We now evaluate our approach using the real AOL
query logs (Pass et al., 2006). We compared our
method Clump with the state-of-the-art transaction
anonymization method Partition (He et al., 2009).
The implementation of both algorithms was done in
Visual C++ and the experiments were performed on
a system with core-2 Duo 2.99GHz CPU with 3.83
GB memory.
5.1 Experiment Setup
Dataset Information. The AOL query log
collection dataset consists of 20M web queries
collected from 650k users over three months in form
of {AnonID, QueryContent, QueryTime, ItemRank,
ClickURL} and are sorted by anonymous AnonID
(user ID). Our experiments focused on anonymizing
QueryContent. The dataset has a size of 2.2GB and
is divided into 10 subsets, each of which has similar
characteristics and size. In our experiment, we used
the first subset. In addition, we merged the queries
issued by the same AnonID into one transaction
because each query is too short, and removed
duplicate items, resulting in 53,058 queries or
transactions with the average transaction length of
20.93.
We generated the item taxonomy T using the
WordNet dictionary (Fellbaum, 1998). According to
the WordNet, each noun has multiple senses. A
sense is represented by a synset, i.e., a set of words
with the same meaning. We used the first word to
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY LOG ANONYMIZATION
115

represent a synset. In pre-processing the AOL
dataset, we discarded words that are not in the
WordNet dictionary. We treated each noun as an
item and interpreted each noun by its most
frequently used sense i.e., the first synset. Therefore,
nouns together with the is-a-kind-of links among
them comprise a tree. The generated taxonomy tree
contains 25645 items and has the height 18. (We
will release the dataset and the taxonomy tree for
research if this work is published.)
We investigate the following four quality
indicators: a) distortion (i.e., information loss), b)
average generalized transaction length, which
reflects the number of items suppressed, c) average
level of generalized items (with the root at level 1),
and d) execution time. The distortion is measured by
ΣGGD(S
i
, LCG(S
i
)) over the clusters S
i
for Clump,
and by ΣGGD(S
i
, t
j
) over the sub-partitions S
i
for
Partition where t
j
is the generalized transaction.
Parameters. The first parameter is the anonymity
parameter k. We set k to 5, 7, 10, and 15. Another
parameter is the database size |D| (i.e., the number of
transactions). In our experiments, we used the first
1000, 10000, and 53,058 transactions to evaluate the
runtime and the effect of “transaction density” on
our algorithm performance. The transaction density
is measured by the ratio N
total
/ (|D||L|), where N
total
is the sum of number of items in all transactions, |D|
is the number of transactions, and |L| is the number
of leaf items in our taxonomy. |D||L| is the
maximum possible number of items that can occur
in |D| transactions. Table 3 shows the density of the
first |D| transactions. Clearly, a database gets sparser
as |D| grows. Unless otherwise stated, we set the
parameter r=10 (a parameter used by Clump).
Table 3: Transaction database density.
|D| 1,000 10,000 20,000 30,000 40,000 53,058
Density 0.28% 0.25% 0.20% 0.16% 0.14% 0.11%
5.2 Results
As discussed in Section 1.1, one of our goals is to
preserve duplicate items after generalization because
duplication of items tells some information about the
number of items in an original transaction, which is
useful to data analysis. To study the effectiveness of
achieving this goal, we consider two versions of the
result produced by Clump, denoted by Clump1 and
Clump2. Clump1 represents the result produced by
Clump as discussed in Section 4, thus, preserves
duplicate items in LCG. Clump2 represents the result
after removing all duplicate items from LCG.
Figures 3, 4, 5 show the results with respect to
information loss, average transaction length, and
average level of generalized items. Below, we
discuss each in details.
Information Loss. Figure 3 clearly shows that the
information loss is reduced by the proposed Clump
compared with Partition. The reduction is as much
as 30%. As we shall see shortly, this reduction
comes from the lower generalization level of the
generalized items in LCG, which comes from the
effectiveness of grouping similar transactions in our
clustering algorithm. However, the difference
between Clump1 and Clump2 is very small. A close
look reveals that many duplicate items preserved by
Clump1 are at a high level of the taxonomy tree. For
such items, generalization has a GGD close to that
of suppressing an item. However, this does not mean
that such duplicate items carry no information.
Indeed, duplicates of items tell some information
about the quantity or frequency of an item in an
original transaction. Such information is not
modelled by the GGD metric.
As the database gets larger, the data gets sparser,
the improvement of Clump over Partition gets
smaller. In fact, when data is too sparse, no
algorithm is expected to perform well. As the
privacy parameter k increases, the improvement
reduces. This is because each cluster contains more
transactions, possibly of different lengths; therefore,
more generalization and more suppression are
required for the LCG of such clusters. Typically, k in
the range of [5,10] would provide adequate
protection.
Average Generalized Transaction Length. Figure
4 shows the average length of generalized
transactions. Clump1 has significantly larger length
than Clump2 and Partition. This longer transaction
length is mainly the consequence of preserving
duplicate items in LCG by Clump1. As discussed
above, duplicate items carry useful information
about the quantity or frequency of items in an
original transaction. The proposed Clump preserves
better such information than Partition.
Average Level of Generalized Items. Figure 5
shows that the average level of generalized items for
Clump2 is lower than that for Partition which is
lower than that for Clump1 (recall that the root item
is at level 1). This is due to the fact that many
duplicate items preserved by Clump1 are at a level
close to the root. When such duplicates are removed
(i.e., Clump2), the remaining items have a lower
average level than Partition.
SECRYPT 2010 - International Conference on Security and Cryptography
116
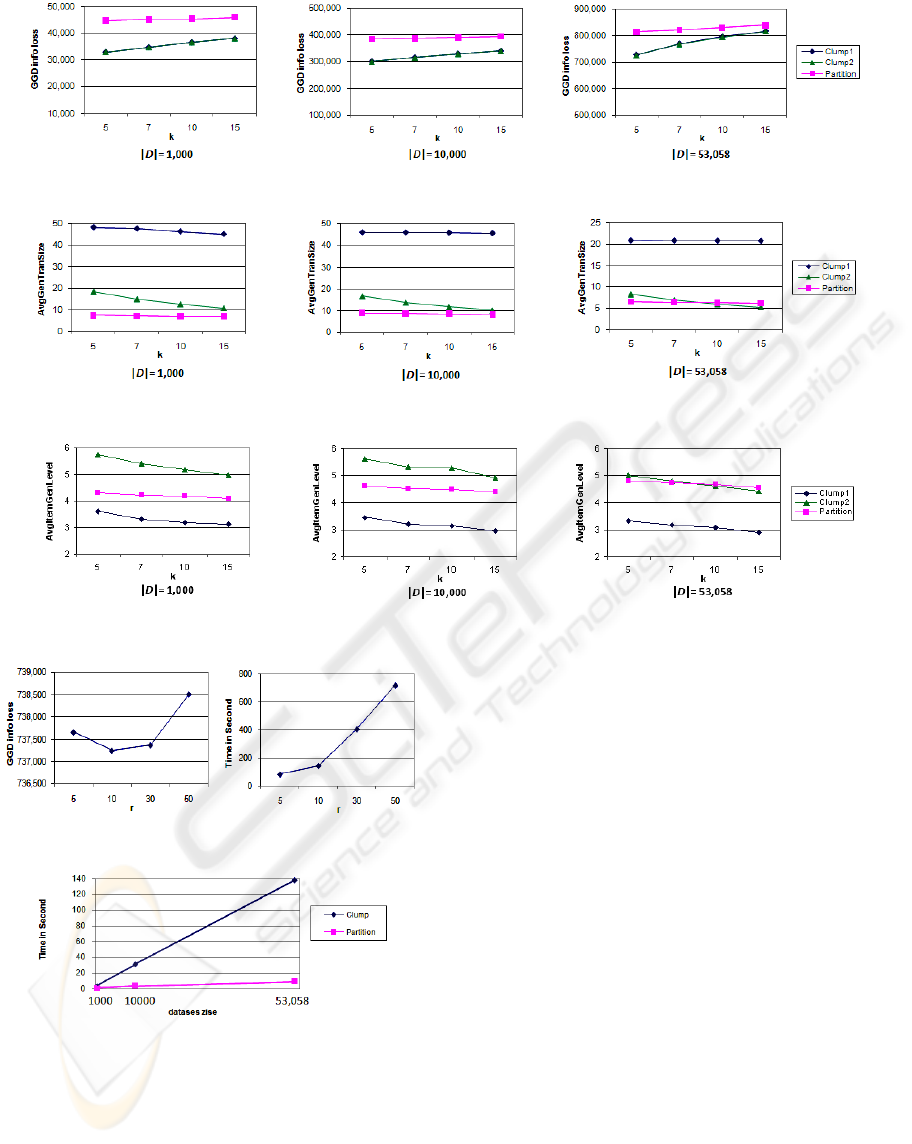
Figure 3: Comparison of information loss.
Figure 4: Comparison of average generalized transaction length.
Figure 5: Comparison of average level of generalized item.
Figure 6: Effect of r on Clump1.
Figure 7: Comparison of running time.
Sensitivity to the Parameter r. This is the number
of top clusters examined for assigning each
transaction. A larger r means that more clusters will
be examined to assign a transaction, thus, a better
local optimal cluster but a longer runtime. In this
experiment, we set |D|=53,058 and k=5. As shown in
Figure 6, we set r to 5, 10, 30, 50, and 100. This
experiment shows that a larger r does not always
give a better result since Clump works in a greedy
manner and by increasing the number of clusters to
examine, we may come up with a locally optimal
choice that later increases the overall information
loss. Our experiments show that r=10 achieves a
good result.
Runtime. Figure 7 depicts the runtime comparison
for k=5 and r=10. Clump takes longer time than
Partition does. In fact, the small runtime of Partition
is largely due to the fact that the top-down algorithm
stops partitioning the data at a high level of the
taxonomy because a sub-partition contains less than
k transactions. Thus, this small runtime is in fact at
the costly information loss. Clump takes a longer
runtime but is still linearly scalable with respect to
the data size. Considering the notably less
information loss, the longer runtime of Clump is
justified.
6 RELATED WORK
A recent survey (Cooper, 2008) discussed seven
query log privacy-enhancing techniques from a
policy perspective, including deleting entire query
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY LOG ANONYMIZATION
117

logs, hashing query log content, deleting user
identifiers, scrubbing personal information from
query content, hashing user identifiers, shortening
sessions, and deleting infrequent queries. Although
these techniques protect privacy to some extent,
there is a lack of formal privacy guarantees. For
example, the release of the AOL query log data still
leads to the re-identification of a search engine user
even after hashing user’s identifiers (Barbaro et al.,
2006). The challenge is that the query content itself
may be used together with publicly available
information for linking attacks.
In token based hashing (Kumar et al., 2007) a
query log is anonymized by tokenizing each query
term and securely hashing each token to an
identifier. However, if an unanonymized reference
query log has been released previously, the
adversary could employ the reference query log to
extract statistical properties of query terms in the log
and then processes the anonymized log to invert the
hash function based on co-occurrences of tokens
within queries.
Secret sharing (Adar, 2007) is another method
which splits a query into k random shares and
publishes a new share for each distinct user issuing
the same query. This technique guarantees k-
anonymity because each share is useless on its own
and all the k shares are required to decode the secret.
This means that a query can be decoded only when
there are at least k users issuing that query. The
result is equivalent to suppressing all queries issued
by less than k users. Since queries are typically
sparse, many queries will be suppressed as a result.
Split personality, also proposed in (Adar, 2007),
splits the logs of each user on the basis of “interests”
so that the users become dissimilar to themselves,
thus reducing the possibility of reconstructing a full
user trace (i.e. search history of a user). This
distortion also makes it more difficult for researchers
to correlate different facets.
The work on transaction anonymization is
studied in the database and data mining
communities. Other than the Partition algorithm (He
et al., 2009) we discussed in Section 1.1, some
techniques such as (h; k; p)-coherence (Xu et al.,
2008), using suppression technique, and k
m
-
anonymity (Terrovitis et al., 2008), using
generalization, have been proposed. Both works
assume that a realistic adversary is limited by a
maximum number of item occurrences that can be
acquired as background knowledge. As pointed out
in (He et al., 2009), if background knowledge can be
on the absence of items, the adversary may exclude
transactions using this knowledge and focus on
fewer than k transactions. The k-anonymity avoids
this problem because all transactions in the same
equivalence class are identical.
7 CONCLUSIONS
The objective of publishing query logs for research
is constrained by privacy concerns and it is a
challenging problem to achieve a good tradeoff
between privacy and utility of query log data. In this
paper, we proposed a novel solution to this problem
by casting it as a special clustering problem and
generalizing all transactions in each cluster to their
least common generalization (LCG). The goal of
clustering is to group transactions into clusters so
that the overall distortion is minimized and each
cluster has at least the size k. We devised efficient
algorithms to find a good clustering. Our studies
showed that the proposed algorithm retains a better
data utility in terms of less data generalization and
preserving more items, compared to the state-of-the-
art transaction anonymization approaches.
ACKNOWLEDGEMENTS
Authors would like to thank Junqiang Liu for his
assistance in implementation part and also reviewers
for their feedback. This research was supported by a
Natural Sciences and Engineering Research Council
of Canada (NSERC) Discovery Grant.
REFERENCES
Adar, E. (2007). User 4XXXXX9: Anonymizing query
logs, In Query Log Workshop, In WWW 2007.
Barbaro, M. and Zeller, T. (2006). A face is exposed for
AOL searcher no. 4417749, In The New York Times.
2006-08-09.
Bayardo, R. J., and Agrawal, R. (2005). Data privacy
through optimal k-anonymization. In ICDE 2005.
Cooper, A. (2008). A survey of query log privacy-
enhancing techniques from a policy perspective, In
ACM Transactions on the Web, Vol. 2, No. 4, 2008.
Fellbaum, C. (1998). WordNet, an electronic lexical
database, In MIT Press, Cambridge MA, 1998.
Fung, B., Wang, K., Chen, R., Yu., P. (2010). Privacy-
preserving data publishing: a survey on recent
developments. ACM Computing Surveys, Vol. 42,
Issue No 4, December 2010
Hafner, K. (2006). Tempting data, privacy concerns;
researchers yearn to use AOL logs, but they hesitate,
In The New York Times. 2006-09-13.
SECRYPT 2010 - International Conference on Security and Cryptography
118

He, Y., and Naughton, J. (2009). Anonymization of set
valued data via top-down, local generalization. In
VLDB 2009.
Iyengar, V. (2002). Transforming data to satisfy privacy
constraints, In SIGKDD 2002.
Kumar, R., Novak, J., Pang, B., and Tomkins, A. (2007)
On anonymizing query logs via token-based hashing.
In WWW 2007.
LeFevre, K., DeWitt, D. J., and Ramakrishnan, R. (2005).
Incognito: Efficient full-domain k-anonymity. In
SIGMOD 2005.
LeFevre, K., DeWitt, D. J., and Ramakrishnan, R. (2006)
Mondrian multidimensional k-anonymity. In ICDE
2006.
Meyerson, A., Williams, R. (2004). On the complexity of
optimal k-anonymity, In PODS 2004.
Pass, G., Chowdhury, A., and Torgeson, C. (2006). A
picture of search, The 1st International Conference on
Scalable Information Systems, Hong Kong, 2006.
Samarati, P. (2001). Protecting respondents’ identities in
microdata releases. In TKDE, vol. 13, no. 6, pp. 1010–
1027.
Sweeney, L. (2002). Achieving k-anonymity privacy
protection using generalization and suppression,
International Journal on Uncertainty, Fuzziness and
Knowledge-based Systems 10 (5), 2002, p.p 571–588.
Sweeney, L. (2000). Uniqueness of simple demographics
in the U.S. population, LIDAP-WP4 CMU,
Laboratory for International Data Privacy, 2000
Terrovitis, M., Mamoulis, N., and Kalnis, P. (2008).
Privacy preserving anonymization of set valued data.
In VLDB 2008.
Xu, Y., Wang, K., Fu, A., and Yu, P. (2008).
Anonymizing transaction databases for publication, In
SIGKDD 2008.
Xu, J., Wang, W., Pei, J., Wang, X., Shi, B., and Fu, A.
(2006). Utility-based anonymization using local
recoding. In SIGKDD 2006.
AN EFFECTIVE CLUSTERING APPROACH TO WEB QUERY LOG ANONYMIZATION
119
