ADAPTIVE MOTION ARTIFACT FILTER FOR

PHOTOPLETHYSMOGRAM EXTRACTION

O. Abdallah, A. Piera Tarazona, T. Martínez Roca, K. Abo Alam and A. Bolz

Institute of Biomedical Engineering, Karlsruhe Instiute of Technology, Germany

Keywords: Adaptive filter, Photoplethysmogram, Motion artifacts, Oxygen saturation, Pulse oximetry.

Abstract: Adaptive filters have been used to enable the robust measurement of photoplethysmogram (PPG) under

conditions of the motion artifact which causes a high noise to the signal. In this adaptive filter a noise

reference and a signal reference are used. The least mean square (LMS) method was applied to extract the

actual signal from the noisy one. For the first approximation to generate the reference signal, a low pass

filter is used. Based on the resulting signal, an appropriate reference signal is generated. This reference

signal is in turn subtracted from the detected signal to generate a noise signal. The generated noise signal is

modified to synthesize the noise reference signal. The synthesized reference noise is adjusted by the

adaptive algorithm to the real one contained in the measurement, and then subtracted from the detected

noisy signal. The filtered signals can be used to determine various physiological parameters such as the

fractional oxygen saturation or the other blood components. Calculating the oxygen saturation using the

filtered PPGs subjected to artifacts looks promising when compared to the calculated values using PPGs

without motion artifacts, for the same case.

1 INTRODUCTION

The photoplethysmogram (PPG) plays a central role

for noninvasive monitoring and early diagnosis. Not

only will PPG and the principle of spectroscopy be

used to calculate oxygen saturation and biochemical

concentrations in blood like hemoglobin and

glucose, but also in combination with other

measured parameters it will be used to calculate

more parameters and hence enables a valuable

diagnosis (

Mendelson, 1992), (Ali-Munive, 2002).

Pulse oximetry is a valuable and widely

employed non-invasive method to monitor oxygen

saturation. But motion artifacts, especially for

monitoring the fractional oxygen saturation, entail

great limitations and often become an

insurmountable obstacle in the utilization of this

technology, since they appear in the same

frequencies as the desired signal and their amplitude

order is quite large compared to the amplitude levels

of pulse signals. Due to this frequencies overlap,

indiscriminate filtering cannot be tolerated, for

reasons of signal clarity preservation (Abdallah,

2003), (Vora, 2004), (Masimo Corporation).

In order to develop a multisensor for diagnosing

cardiovascular diseases and computing the fractional

oxygen saturation, an adaptive filter, that allows the

detection of the PPG by one or more sensors under

conditions of motion artifacts, has been explored. By

this way, it will be possible to establish the

fractional oxygen saturation values even under

motion circumstances. The main advantage of the

algorithm implementing the adaptive filter is that it

needs just one PPG.

To develop a full-featured system successfully

without any other help, else one PPG signal, an

implementation based on a noise cancellation

configuration is carried out and the noise reference

necessary for its proper operation is synthesized

from the PPG signal itself. Amongst all the possible

adaptive algorithms that can be used, due to its low

computational cost, the Least Mean Square

algorithm has been selected, which improves the

quality of the PPGs by cancelling the effects of

motion artifacts.

Many experiments are performed to test the

capabilities of the proposed system. The results

indicate that the effects of motion artifacts are to a

large extent cancelled and the recovered PPG

signal’s quality is good enough for measuring the

fractional oxygen saturation of the haemoglobin in

blood. Further blood contents like glucose and

physiological parameters can be extracted in a way

187

Abdallah O., Tarazona A., Roca T., Alam K. and Bolz A. (2010).

ADAPTIVE MOTION ARTIFACT FILTER FOR PHOTOPLETHYSMOGRAM EXTRACTION.

In Proceedings of the Third International Conference on Biomedical Electronics and Devices, pages 187-190

DOI: 10.5220/0002743901870190

 SciTePress

that could allow monitoring them under artifacts.

2 METHOD

When a conventional adaptive filter system has to be

used, the first requirement consists of having two

signals:

• The input signal coming from the sensor.

• A reference signal that has to be an ideal version

of the input signal, as the adaptive algorithm

works to make the input signal as similar as

possible to the reference signal.

The first decision was to reject the use of a

conventional adaptive filter implementation, because

a priori there is no reference pulse signal for a given

person at every moment. So, we considered an

adaptive noise cancellation system as possible

solution. But, when we use an adaptive noise

cancellation system, two input signals are needed

again; now they are:

• The input signal or, expressed in other words, the

measurement coming from the sensor. That is to

say, the same requirement as the one presented

above.

• A noise reference signal that must be similar to the

real noise that our measurements contain, but not

necessarily equal to it, as in this case, the filter

tries to eliminate this real noise while leaving the

desired signal (pulse signal) unchanged. That is a

great advantage compared to having to generate a

perfect pulse signal, as unlike synthesizing a pulse

reference, synthesizing a noise reference similar to

the real noise coming from the sensor is actually

feasible.

We do not have that noise reference signal at our

disposal, and this fact leads us to synthesize this

second input by designing a synthesizer.

Figure 1: Block diagram of the Main Program.

A broad outline of the implementation of the

algorithm that has been devised is given in Figure 1,

where the interaction between the two principal

cornerstones of the design, the Adaptive Noise

Cancellation System and the Noise Reference

Synthesizer, can be noticed. Once we have correctly

generated a Noise Reference Signal by means of the

Synthesizer, it will be adjusted as much as possible

to the real noise contained in the corresponding

measurement by the adaptive filter. In our case, this

filter is composed of a noise cancellation

configuration which uses a Least Mean Square

algorithm as adaptive algorithm. What we get as

output from the system is a denoised pulse signal.

Figure 2: Block diagram of the Synthesizer.

The Synthesizer generates a Noise Reference, which

is necessary for the Adaptive Noise Cancellation

System, by means of generating an ideal pulse

signal, called Pulse Reference Signal. Figure 2

presents the basic block diagram of this Synthesizer.

Given that the Reference Signal has to follow the

Input Signal, it has to be created according to the

current Input Signal at each moment. For that

reason, it is, first of all, required to know the number

of periods that the corresponding Input signal has.

Therefore, in the Minima Detection block we search

and find all the pulse minima locations in the Input

Signal, since there are as many periods as there are

minima–1. In order to generate a more reliable

Reference Signal, the amplitude values of these

minima are also calculated along with the locations

and amplitude values of the maxima appearing in the

Input Signal, using the Maxima Detection block.

Each minimum and maximum’s amplitude are

adjusted to the corresponding Input Signal period.

Using the Interpolation block, the Reference Signal

is generated with as many periods as the current

Input Signal and with the same amplitude. Once this

pulse reference signal, Reference Signal, is

generated, we are able to obtain a noise model by the

following equation:

Noise Reference=Input Signal - Reference Signal (1)

As previously mentioned, an adaptive noise

cancellation system has two inputs, as shown in

Figure 3. One is the Input Signal, i.e. the signal

BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices

188

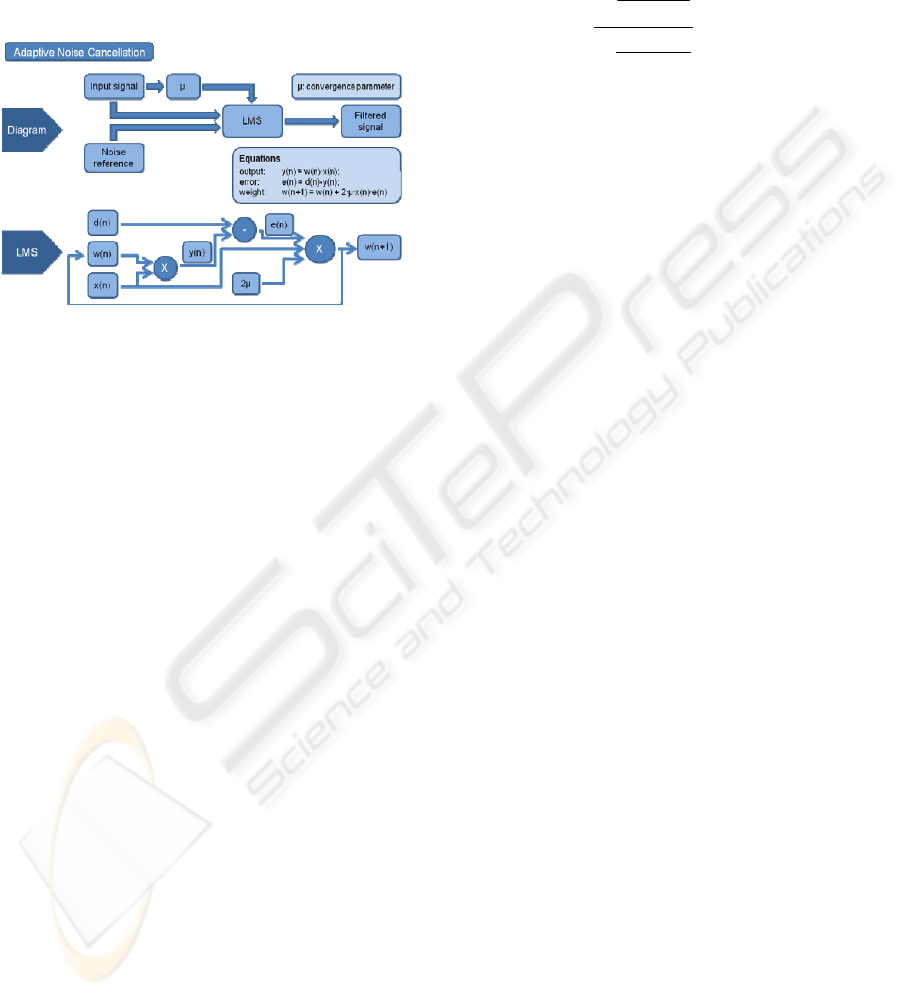
corrupted by noise, coming from the sensor, and the

other one is the Noise Reference, coming from the

Synthesizer output. Given that the Least Mean

Square algorithm provides adaptive filtering, the

Noise Reference is adjusted to the real noise

measured by the sensor and, as a result, the output,

Filtered Signal, naturally is the denoised signal.

Figure 3: Block diagram of the Adaptive Noise

Cancellation (ANC).

3 RESULTS

To make possible SpO2 measurements, we need to

compare two PPGs at the same time with two

different wavelengths. For that reason, we required a

multi-wavelength featured sensor such as the PHM

used at the institute's laboratory, which has eight

different LEDs.

In order to test our system capabilities, it was

essential to obtain somehow measurements with the

employed PHM sensor that simulates those taken in

real situations in which PPGs presents drawbacks

that make computing medical parameters by means

of photoplethysmography unfeasible.

With the purpose of simulating these kinds of

conditions at our laboratory, the sensor was

subjected to movement, thereby emulating typical

motion artifacts that are usually presented in the

pulse signal when it is measured under extreme

conditions such as within a moving ambulance.

The measurements were carried out alternatively

between intervals of time without movement and

intervals with movement of the finger, hand and

even arm varying in speed and intensity. Each

measurement from this PHM sensor contains as

many signals as LEDs on. Since we need two of

them, first we have to separate the signals. Once

these single signals are presented separately, we

select two of them that have been measured with the

proper wavelengths value like 970 nm and 660 nm.

Then they are already adapted for being filtered by

our system. Finally, the filtered signals obtained

after the program execution can already be used to

compute ratios regarding the SpO2, such as the so-

called Ω ratio:

(,)

Ω=

(2)

Where:

I(λ

, t

), I(λ

, t

), I(λ

, t

) and I(λ

, t

) are the light

intensities measured at the instants t

and t

, with the

wavelengths λ

and λ

, respectively.

As results, examples of each step of the process

described here are presented. First of all, examples

of the appearance of PHM measurements (and

therefore, multi-wavelength measurements) are

shown, both the whole measurement and a zoom of

it. Next, the output given by the recovery of each

single signal coming from only one LED is also

presented. To demonstrate the ability of the

proposed system to make possible a precise enough

computation of the SpO

, we have calculated the

value of the above-named Ω ratio for several

measurements. In order to make sure that the

adaptive filter works well enough to get accurate

SpO

readings, the main goals are: first, to prove that

the ratios obtained are included in an acceptable

range (bearing in mind that the values of this ratio

allow us to estimate the calibration that has to be

applied later to the exact calculation of the SpO

Next, it must be proved that the values for the ratio

when the signal is affected by motion artifacts keep

quite unchanging compared to those stretches of the

same signal where there is no noise.

Figure 4, shows the PHM measurements. There

are seven emitting diodes; each signal coming from

each LED presents a different mean amplitude level

and a reference level. After the recovery of each

single signal, and once the reference level has been

subtracted, the outcome of the Figure 5 is given,

which is the result of recovering each single signal

contained in the previous measurement.

From the group of four graphs on the top of the

Figure 6, the two on the left are parts (delimited by

and t

) without noise of two signals from the same

PHM measurement, corresponding to the signal

coming from the LED configured with infrared

wavelength and the LED configured with red

wavelength.

ADAPTIVE MOTION ARTIFACT FILTER FOR PHOTOPLETHYSMOGRAM EXTRACTION

189

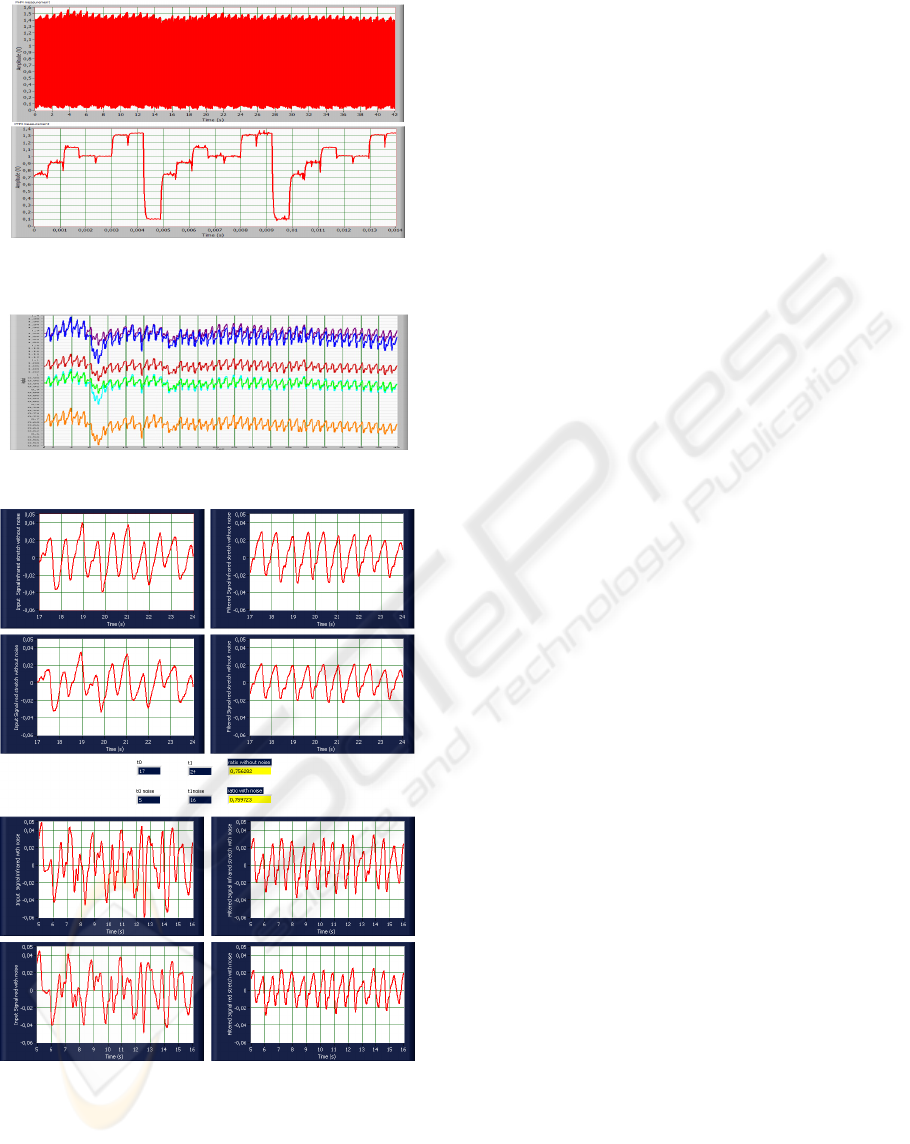
Figure 4: PHM measurement and detail of the different

signals appearing in the PHM measurement.

Figure 5: Signals recovered from a PHM measurement.

Figure 6: LabVIEW printing for filtering a PHM

measurement and computing Ω .

The two plots on the right are the result of filtering

these two signals. Analogously, the group of four

graphs on the bottom represents two parts (delimited

by t

noise and t

noise) with noise of the same two

signals from the same PHM measurement. In the

middle, the two values for the ratio Ω, one

corresponding to the noisy stretch of the signals and

the other one corresponding to the clean stretch are

presented.

4 CONCLUSIONS

Both, for long-term and short-term monitoring (for

example, in case of an emergency) of biosignals, the

use of an adaptive filter becomes essential. The

developed algorithm implementing the adaptive

filter is applicable to the PPG signal, which is

needed for the computation of several vital

parameters (such as SpO2, HR and blood pressure

fluctuations) and also for diagnosing. In fact, the

results indicate that the signal recovered from this

implementation has enough quality for measuring

the fractional oxygen saturation of the haemoglobin

in blood.

Furthermore, after a few modifications, this

algorithm can be used for electrocardiogram (ECG)

and it is also possible to carry out more adjustments

to other parameters such as electroencephalogram

(EEG), electrooculogram (EOG) and fetal ECG

(FECG).

REFERENCES

Abdallah, O., 2004, Optical Non-invasive Calculation of

Hemoglobin Components concentrations ans

Fractional oxygen Saturation Using a Ring Scatterin

Pulse Oximeter, Proc. of the SPIE-Photonics West

(BIOS), Volume 5325, pp. 51-61, San Jose, USA.

Ali-Munive A., Rodriguez P., Gomez S., Arce A. M. and

Rodriguez E., 2002, Correlación entre Pulsioximetría

y Saturación Arterial de Oxïgeno en Pacientes en

Cuidado Intensivo, Bogotá.

Masimo Corporation, http://www.masimo.com

Mendelson Y., 1992, Pulse Oximetry: Theory and

Applications for Noninvasive Monitoring, Clinical

Chemistry, Vol. 38, No. 9, pp. 1601-1607, Worcester.

Vora Vadana A. and Ahmedzai, S. H., 2004, Pulse

Oximetry in supportive and palliative care, Vol. 12,

No. 11, pp. 758-761, Sheffield, UK.

BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices

190