IMPROVED 2D MAXIMUM ENTROPY THRESHOLD

SEGMENTATION METHOD BASED ON PSO

Liping Zheng

School of Computer Science, Liaocheng University, Liaocheng, Shandong, China

Guangyao Li

CAD Research Center, Tongji University, Shanghai, China

Jing Liang

School of Electrical Engineering, Zhengzhou University, Zhengzhou, Henan, China

Quanke Pan

School of Computer Science, Liaocheng University, Liaocheng, Shandong, China

Keywords: Image segmentation, Entropy, PSO algorithm, Gray probability.

Abstract: Image segmentation plays an important role in the field of image processing. Threshold segmentation is a

simple and important method in image segmentation. Maximum Entropy is a common threshold

segmentation method. In order to adequately utilize gray information and spatial information of image, an

improved 2D entropy computation method is proposed. Otherwise, Particle Swarm Optimization(PSO)

algorithm is used to solve maximum of improved entropy. Maximum takes as the optimal image

segmentation threshold. In this paper, two CT images were segmented in experiment. Experimental results

show that this method can quickly and accurately obtain segmentation threshold. Otherwise, this method has

strong anti-noise capability and save computation time.

1 INTRODUCTION

Image segmentation is to separate pixel of the image

into some non-intersecting regions(Pal, 1993).

Image segmentation is the base of image processing.

Because of the complexity and diversity of image,

there isn’t a common segmentation algorithm. In

application, different algorithms are used according

to features of image and application purposes.

Threshold segmentation method is a widely used

and effective method for segmentation gray level

image. Segmentation results rely on the

segmentation threshold value. Therefore it is very

important to choose an optimal threshold value.

1.1 Threshold Segmentation Method

Threshold segmentation method is one of the most

essential methods in image segmentation. This

method utilizes features of pixels. That is said,

object pixels and background pixels of image can be

distinguished by their gray level values. In process

of segmentation, the histogram of the image is

usually used, other image information such as the

spatial information is not utilized(Glasbey, 1993).By

choosing an adequate threshold value and

segmentation image, object can be extracted from

their background. Selection criterion of

segmentation threshold value plays an important role

in threshold segmentation method.

In past years, many schemes have appeared in

literature. Many different selection criterions were

proposed, such as Otsu method(Otsu, 1979),

minimum error threshold value method(Kittler,

1986). In 1980, entropy-based selecting approach

was proposed(PUN, 1980). Kapur proposed the

one-dimension entropy threshold value

method(Kapur, 1985). When segment an image,

one-dimension threshold value method solely

depended on the gray-level distribution. While the

Signal-to-Noise of image is low and the background

of image is complex, segmentation results with

287

Zheng L., Li G., Liang J. and Pan Q. (2009).

IMPROVED 2D MAXIMUM ENTROPY THRESHOLD SEGMENTATION METHOD BASED ON PSO .

In Proceedings of the International Joint Conference on Computational Intelligence, pages 287-291

DOI: 10.5220/0002314302870291

 SciTePress

one-dimensional entropy segmentation method are

poor. Therefore, Abutaleb proposed two-dimension

entropy method in 1989(Abutaleb, 1989).

The two-dimension entropy is obtained from the

two-dimension histogram which is constructed with

using the gray value of image and the average gray

value of image. Two-dimension entropy method is a

region-dependent method. When computing optimal

threshold value, two-dimension entropy method

needs cost more time than one-dimension entropy

method.

In order to reduce the computation time and

improve accuracy of segmentation threshold value,

an improved 2D maximum entropy threshold

segmentation method is proposed. This method

narrows down the search space. And PSO algorithm

is used to solve the optimal segmentation threshold

value. PSO algorithm has advantages of quick

convergence. Therefore it can reduce computation

time. Improved 2D entropy is called spatial

difference attribute information value entropy

(SDAIVE). This improved threshold segmentation

method based on PSO is called PSO-SDAIVE

algorithm.

2 IMPROVEMENT OF 2D GRAY

HISTOGRAM

While segment image with 2D threshold value

method, associated entropy need to be computed and

obtain the optimal segmentation threshold

value(Sahoo, 1988). In order to reduce the solving

time and improve the searching efficiency, the 2D

gray histogram is improved in this paper.

2.1 2D Gray Histogram

In 2D gray histogram, the horizontal axis is the

gray-level value of pixel. It’s range is [0, L-1]; the

vertical axis is the average gray-level value of pixel.

It’s range is [0,L-1]. Let f(m,n) denotes the

gray-level value of pixel which located at point(m,n).

In image,

{ ( , ) | {1, 2,.... }, {1, 2,.... }}

mn m M n N∈∈.

Let g(m,n) is the average gray-level value of the

neighborhood of pixel(m,n). The whole number of

probability value of

((,),(,))

mn gmn is

In the plan of 2D gray histogram, object pixels

and background pixels locate the diagonal

neighborhood. Noise points and edge pixels are far

from diagonal.

2.2 2D D-value Attribute Gray

Histogram

In traditional 2D gray histogram, the search space is

big and the solving time of the optimal threshold

value is long. In order to narrow down the search

space, 2D gray histogram is improved. According to

pixel attributes, the searching region is reduced.

This improved 2D gray histogram is called 2D

D-value attribute gray histogram. The horizontal

axis of 2D D-value attribute gray histogram is gray

value. The vertical axis is the D-value between gray

value and average gray value. It denotes absolute

value of the difference between

(,)

and

(,)

mn .

The histogram with a given attribute is called

attribute histogram. In this paper, the associated

attribute condition is set. Suppose

(,)

fmn L<<

and

(,) (,)fmn gmn

−

< .The attribute condition

restricts the range of search space. That is the gray

value of pixel is between L

and L

. The average

gray value is also in given range. Only pixels which

satisfy attribute condition can be searched.

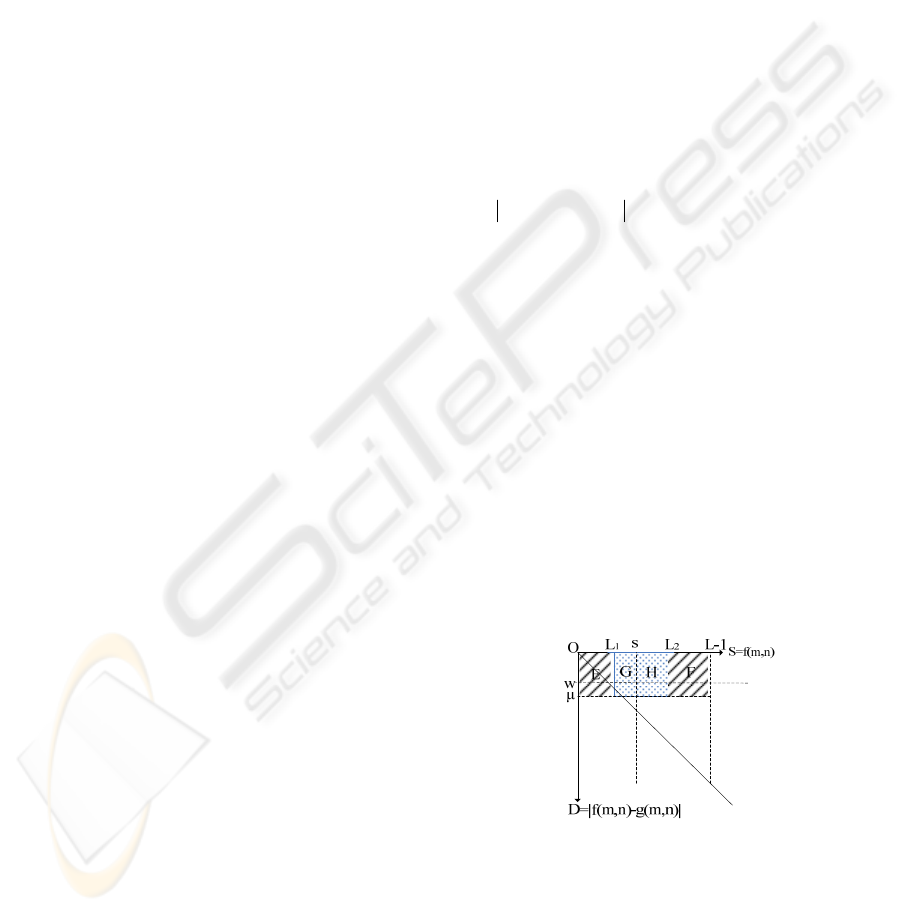
Figure1 shows the plan of 2D D-value attribute

gray histogram. According to attribute condition,

pixels in region G are searched. A pair of value (s,w)

represents segmentation threshold value. Impact of

noise points are reduced by using this improved gray

histogram.

Comparing with the traditional 2D gray

histogram, pixels in region G should satisfy the

following conditions:

(,)Lfmns

≤

≤ and

max{0, } ( , ) min{ , 1}Lw gmn swL

−

≤≤+−. Pixels

in region H should satisfy

1(,)

fmn L+≤ ≤ and

max{0, 1 } ( , ) min{ , 1}swgmn LwL

−≤ ≤ + −.

Figure 1: The plan of 2D D-value attribute gray histogram

3 THE IMPROVED 2D ENTROPY

The essence of image segmentation with entropy is

that utilize the gray probability of image. The gray

information of image includes the gray probability

IJCCI 2009 - International Joint Conference on Computational Intelligence

288

and associated gray value. Spatial information value

includes gray value, average gray value and other

information. In order to better utilize the gray and

spatial information of image, the improved

computation method of 2D entropy is proposed in

this paper.

3.1 Spatial Information Function

According to gray value i and average gray value j,

spatial information function is defined. When

computing image 2D entropy, pixel spatial

information value substitutes for gray probability.

Formula (1) shows computation of spatial

information function. In formula, IV denotes other

spatial gray value.

{

}

12 3

123 1 2 3

(, ) ( 1) ( 1)

1, 0 1, 0 1, 0 1

ij ij

Iij I c i c j cIV p

ccc c c c

== ++ ++

++=≤≤≤≤≤≤

(1)

In this paper, only consider gray value and

average gray. Suppose weights of gray and average

gray are same. Therefore, spatial information

function formula is reduced as formula (2).

( , ) 0.5( 1) 0.5( 1)

ij ij

Iij I i j p== + + +

(2)

Suppose m

is the total number of occurrence

(i,j). The joint probability function p

is defined as

formula(3).

, 0,1,..... 1

ij ij

Mmp

ij L

−−

=−

∑∑

(3)

Refer the 2D D-value attribute gray histogram

and compute the information value entropy. This

entropy is called spatial difference attribute

information value entropy (SDAIVE).

3.2 Computation of SDAIVE

Suppose threshold value pair (s,w), that is said, the

gray value is s, and the gray D-value is w.

According to figure 2, the gray value range and the

gray D-value range are confirmed.

Formula (4) defines the SDAIVE of object pixels

and background pixels. H’(O) is the SDAIVE of

object pixels. H’(B) is the SDAIVE of background

pixels.

'( ) ln

HO P

HB P

(4)

Formula (5) defines computation of P

. Formula

(6) defines P

denotes the gray information

quantity while gray value range is [L

,s]. P

denotes

the gray information quantity while gray value range

is [s+1,L

]. Formula (7) defines H

and H

(1) ( 1)

sws

OO ij

iLjL w

sws

iLjL w

PI I

==−

+++

∑∑

(5)

(1) ( 1)

LwL

BB ij

is js w

LwL

is js w

PI I

=+ =+−

+++

∑∑

(6)

sws

Oijij

iLjL w

ij ij

is js w

==−

=+ =+−

=−

∑∑

(7)

Formula (8) defines discriminant function of

SDAIVE. In this paper, the maximum of SDAIVE is

taken as the selection criterion of threshold value.

Formula (9) defines the maximum function.

Solve the maximum of SDAIVE with some

optimize algorithm and obtain the optimal

segmentation threshold. Then segment image with

the optimal threshold value (s,w)

(, ) '( ) '( )

(ln)

ln(

sws

ij ij

sws

iLjL w

sws

iLjL w

LwL

ij ij

LwL

is js w

LwL

is js w

sws

ij ij

iLjL w js

sw H O H B

==−

=+ =+−

==− =+

−

=×

∑∑

)

(ln)

ln( )

LwL

is w

LwL

sws

ij ij

iLjL w

is js w

sws L wL

iLjL w

is js w

=+ −

==−

=+ =+−

==−

=+ =+−

−

=×++

∑∑

(8)

(, ) ( (, ))

LsL wu

wArgMax sw

<< < <

(9)

4 SEARCHING SEGMENTATION

THRESHOLD WITH PSO

In this paper, PSO algorithm is used to solve the

IMPROVED 2D MAXIMUM ENTROPY THRESHOLD SEGMENTATION METHOD BASED ON PSO

289

SDAIVE maximum. PSO algorithm was jointly

proposed by the American sociologist and

psychologist of James Kennedy and electrical

engineer Russell Eberhart in 1995. The basic idea of

PSO algorithm was inspired by researching results

of behavior about bird groups and makes use of a

biological communities model which was proposed

by biologist Frank Heppner.

4.1 Basic Concepts of PSO Algorithm

PSO algorithm is a Swarm Intelligence Algorithm. It

takes particle as individual and flight with a certain

speed in the search space. These particles haven’t

quality and volume. Every particle has the simple

rules of conduct. According to the flying experience

of individuals and groups, particles can dynamically

adjust the flying speed.

Since 1995, researchers proposed different

algorithm models in different fields. Kenney

constructed simple PSO model. Eberhart

constructed PSO model with inertia weight factor.

YuhuiShi and Clerc constructed PSO model with the

shrinkage factor. Through a large number of

experimentations, the significance and role of

different control parameters in models were detailed

analysis. Corresponding reference values were

identified(Carlisle, 2001).

In PSO algorithm model, choices of parameters

are the focus of researching. There are six important

control parameters in PSO algorithm. They are

population size、cognitive learning rate c

、social

learning rate c

、the maximum of particle flying

speed

max

, the inertia weight factor

、constriction

factor K. The population size of particles refers the

number of particles in iterative process.

In these algorithm models, the basic and earliest

PSO model was defined by Eberhart and

Kennedy(Kennedy, 1995). It was called simple PSO

model. The specific model as formula (10):

( 1) () ( () ())

(() ())

(1) () (1)

id id id id

gd id

id id id

vt vt crPt xt

cr P t x t

xt xt vt

+= + −

+−

+= + +

(10)

4.2 Computation of Optimal Threshold

with simple PSO

In this paper, the simple PSO algorithm was used.

Because the sum of c

and c

should be 4, the

parameters c

＝c

＝2，r

＝r

＝0.5. In experiment,

the iterative formula of speed is simplified as

formula (11):

(1) () () ()2()

id id id gd id

vt vt Pt Pt xt

=++ −

(11)

Because gray value of pixel is integer, the

solving of SDAIVE maximum can take as integer

planning problem. Pixel particles move along the

gray value(V-direction) and the gray D-value(μ

-direction) at the same time. Speed and location of

particles need iterate in two directions at the same

time.

In this paper, t denotes the particle generation. i

denotes serial number of particle.

denotes the

speed change in gray value direction.

denotes

the speed change in gray D-value direction.

denotes the location change in gray value

direction

denotes the location change in gray

D-value direction.

()

and

()

are the

corresponding particle locations of the SDAIVE

maximum in t generation.

Iterative formulas of speed and location as

following:

(1)()() 2()

iv iv iv gv iv

vt vt Pt P xt

=++−

(12)

(1) () (1)

iv iv iv

xt xt vt

=++

(13)

(1)()() 2()

iiigi

vt vt Pt P xt

μμμμμ

=++−

(14)

(1) () (1)

iii

xt xt vt

μμμ

=++

(15)

By iteration, the location of SDAIVE maximum

is confirmed. That is said, the location of optimal

threshold is confirmed.

5 EXPERIMENT AND RESULTS

In order to validate the capability of algorithm which

is proposed in this paper, gray image needs be

segmented in experiment. CT image is a kind of gray

image. Therefore, two CT images were segmented in

experiment. Experiment results were analyzed.

Input two head CT image IM10 and IM10’. The

type of image is uint16. The gray range is [0, 65535].

Image IM10 hasn’t noise. IM10’ has ‘salt & pepper’

noise. Figure2 shows two head CT images.

In this experiment, bones need to be separated

from CT images. Therefore, bones were taken as

object and other tissues were taken as background.

Figure3 shows the 2D D-value attribute gray

histogram of IM10 and IM10’. According to

improved gray histogram, computed their H’(O) and

H’(B) of two images. The SDAIVE maximum of

image was solved with PSO. At last, optimal

IJCCI 2009 - International Joint Conference on Computational Intelligence

290

segmentation threshold values were obtained.

Figure 2: Input IM10 and IM10’.

Figure 3: The 2D D-value attribute gray histogram.

The optimal threshold value of IM10 is (2253,

500). The optimal threshold value of IM10’ is (2275,

525). Figure 4 shows the segmentation results of two

images.

Figure 4: The segmentation results of IM10 and IM10’.

Experiment results show that this improved

segmentation method has good anti-noise capability.

Otherwise, the search space is small. The time of

solving optimal threshold value is decreased. If

using genetic algorithm, the computation quantity is

also reduced, but the genetic algorithm is complex.

6 CONCLUSIONS

The one-dimension entropy method only considers

gray information. Otherwise, it has poor anti-noise

capability. Two-dimension entropy method considers

the spatial information, but the computing quantity

is large.

Improved 2D maximum entropy threshold

segmentation method based on PSO is called

PSO-SDAIVE algorithm. This algorithm not only

considers the spatial information, but also considers

the gray information and decreases the computing

quantity. Otherwise, the neighboring pixel control

parameter is set. The overly-smoothness of images

can be avoided.

In this paper, simple PSO model is used. In

future, we will research the solving method of

SDAIVE with different PSO models and search an

optimal PSO model with shortest time.

ACKNOWLEDGEMENTS

Subject is supported by National Natural Science

Foundation of China. The serial number is 60771065

and 60874075.

REFERENCE

Pal N R., Pal S K., 1993. A review on image segmentation

techniques. Pattern Recognition.

Glasbey, CA., 1993. An analysis of histogram-based

thresholding algorithms, CVGIP: Graphical Models

and Image Process.

Otsu N., 1979. A threshold value selection method from

grey-level histograms, IEEE Trans. System.

Kittler J. Illingworth M., 1986. Minimum error

thresholding. Pattern Recognition.

Pun T.,1980. A new method for grey-level picture

thresholding using the entropy of the histogram.

Signal Process.

Kapur J. N., Sahoo P.K., Wong A., 1985. A new method

for gray-level picture thresholding using the entropy of

the histogram. Computer Vision Graphics and Image

Processing.

Abutaleb A S.,1989. Automatic thresholding of gray-level

picture using two-dimensional entropies. Pattern

Recognition.

Sahoo P K, Soltani S., 1988. A svrvey of thresholding

techniques. Comput. Vision Graphics and Image

Process.

Kennedy J, Eberhart R. C., 1995. Particle Swarm

Optimization. In: Proc. IEEE Int’l. Conf. on Neural

Networks, IV. Piscataway, NJ: IEEE Service Center

Carlisle A, Dozier G., 2001. An Off-the-shelf PSO. In

Proceedings of the Workshop on Particle Swarm

Optimization. Indianapolis, IN: Purdue School of

Engineering and Technology, IUPUI(in press).

IMPROVED 2D MAXIMUM ENTROPY THRESHOLD SEGMENTATION METHOD BASED ON PSO

291