A PRUNING BASED ANT COLONY ALGORITHM FOR

MINIMUM VERTEX COVER PROBLEM

Ali D. Mehrabi

, Saeed Mehrabi

†

and Abbas Mehrabi

‡

Department of Mathematical and Computer Sciences, Yazd University, Yazd, Iran

†

Department of Computer Science, Shahid Bahonar University of Kerman, Kerman, Iran

‡

Department of Computer Engineering, Islamic Azad University, South Tehran Branch, Tehran, Iran

Keywords: Minimum vertex cover problem, Meta-heuristic approaches, Ant colony optimization algorithms.

Abstract: Given an undirected, unweighted graph G = (V , E) the minimum vertex cover (MVC) problem is a subset

of V whose cardinality is minimum subject to the premise that the selected vertices cover all edges in the

graph. In this paper, we propose a meta-heuristic based on Ant Colony Optimization (ACO) approach to

find approximate solutions to the minimum vertex cover problem. By introducing a visible set based on

pruning paradigm for ants, in each step of their traversal, they are not forced to consider all of the remaining

vertices to select the next one for continuing the traversal, resulting very high improvement in both time and

convergence rate of the algorithm. We compare our algorithm with two existing algorithms which are based

on Genetic Algorithms (GAs) as well as its testing on a variety of benchmarks. Computational experiments

evince that the ACO algorithm demonstrates much effectiveness and consistency for solving the minimum

vertex cover problem.

1 INTRODUCTION

1.1 Minimum Vertex Cover Problem

Given an undirected, unweighted graph G = (V , E),

the minimum vertex cover problem is to find a

subset of V such that for each edge in E, at least one

of its two end vertices is in the subset and that its

cardinality is minimum. Formally, given an

undirected, unweighted graph G = (V , E), the

minimum vertex cover problem seeks to find a

subset

VV ⊆'

satisfying

Eve

∈

)(

∪

, where

)(ve

denotes the edges incident on vertex v, such

that

is minimized.

In (Karp, 1972) the decision version of the

minimum vertex cover problem had been shown as

NP-complete. After then, the vertex cover problem

is one of the core NP-complete problems that have

been frequently used for delivering to NP-hardness

(Gary and Johnson, 1979). In practice, the minimum

vertex cover problem can be used to model many

real world situations in the areas of circuit design,

telecommunications, network flow and so on. For

example, whenever one wants to monitor the

operation of a large network by monitoring as few

nodes as possible, the importance of the MVC

problem comes into the rule (Papadimitriou and

Steiglitz, 1982).

Due to the computational intractability of the

problem, many researchers have instead focused

their attention on the design of approximation

algorithms for delivering quality solutions in a

reasonable time. An intuitive greedy approach for

solving the problem is to successively select the

vertex with the largest degree until all of the edges

are covered by the vertices in V'. This

straightforward heuristic is not a good one as

demonstrated by (Papadimitriou & Steiglitz 1982, p.

407). They considered regular graphs, each of which

consists of three levels. The first two levels have the

same number of vertices while the third level has

two vertices less than the number of vertices found

on the previous two levels. The regular graph for

k=3 can be found in (Papadimitriou and Steiglitz,

1982). As (Papadimitriou, 1994) shows, this greedy

algorithm never produces a solution which is more

than

)ln(n times the optimum, where n is the

number of vertices. However, the best

281

D. Mehrabi A., Mehrabi S. and Mehrabi A. (2009).

A PRUNING BASED ANT COLONY ALGORITHM FOR MINIMUM VERTEX COVER PROBLEM.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 281-286

DOI: 10.5220/0002313802810286

 SciTePress

approximation algorithm known for the minimum

vertex cover problem has been reported in (Khuri

and Back, 1994), in which at each iteration, we

randomly choose an edge, say

),( vu and add its

end points to current vertex cover being constructed

deleting them from the graph. The algorithm reveals

a performance guarantee of 2. As a part of our

experimental results, we compare our proposed

algorithm with two existing algorithms based on

GAs on this type of graphs. Finally (Dinur and

Safra, 2001) show that it is impossible to attain

approximate solutions to the minimum vertex cover

problem within any factor smaller than 1.36067,

unless

.NPP = After this, the meta-heuristic

approaches for solving the problem come into the

role.

In solving the minimum vertex cover problem,

we also have a solution for another graph problem:

The maximum independent set (MIS) problem (exact

definition of this problem can be found in (West,

2001), for example). The close relationship between

these problems is shown by the following Lemma

(see e.g. (Papadimitriou and Steiglitz, 1972)):

Lemma 1. For any graph G = (V , E) and V' ≤ V, the

following statements are equivalent:

● V' is the minimum vertex cover in G.

● V – V' is the maximum independent set of G.

Consequently, one can obtain a solution of the

maximum independent set problem by taking the

complement of solution to the minimum vertex

cover problem (Hifi, 1997). However, many meta-

heuristic approaches for solving the MIS have been

used, so far. Specifically, we have used a hybrid GA

for its solving which results in very near to optimum

solutions for a variety of large scale MIS problem

benchmarks (Mehrabi and et al., 2009).

1.2 Ant Colony Optimization

In the optimization literature, meta-heuristic also

foster a viable alternative for delivering quality

approximate solutions (Mehrabi and Mehrabi, 2009).

Like genetic algorithms, simulated annealing and

tabu search, the Ant Colony Optimization (ACO) is

a meta-heuristic using natural metaphor to solve

complex combinatorial optimization problems such

as the traveling salesman problem, graph coloring

problem (Costa and Hertz, 1997) and so on. The

general framework of the ACO algorithms is

presented in Fig. 1. Basically, the problem under

study is transformed into a weighted graph. Then,

the ACO algorithm iteratively distributes a set of

artificial ants onto the graph to construct the paths

corresponding to potential optimal solutions.

The optimization mechanism of the ACO is

based on two important features: The state transition

rule and the pheromone updating rule. The first one,

which is a probabilistic operation, is applied when

an ant is choosing the next vertex to visit. The

second one dynamically changes the preference

degree for the edges that have been traversed

through. As the literature shows, apply these two

simple parts of an ACO can solve many complex

optimization problems. This paper also explains

their role in algorithm by next section.

2 THE ACO ALGORITHM

As we mentioned, the structure of MVC problem is

different from those of problems which have been

solved by ACO in literature. In fact, the solution to

MVC is an unordered subset of vertices obtained by

each ant, while the most ACO-based solvers so far

get the solution as an ordered or unordered subset of

edges (Dorigo and Gambardella, 1997). So it

becomes more challenging and desirable to

transform the MVC problem characteristics into an

appropriate graph representation. Also, the

implementation of a standard ACO phases,

providing an efficient local heuristic for the state

transition rule and the design of pheromone updating

rule becomes an important issue. We devoted this

section for presenting our implementations in detail.

Figure 1: The outline of an ACO algorithm.

2.1 Graph Representation

Suppose that G = (V , E) denote the underlying

graph for MVC problem and the solution to this

IJCCI 2009 - International Joint Conference on Computational Intelligence

282

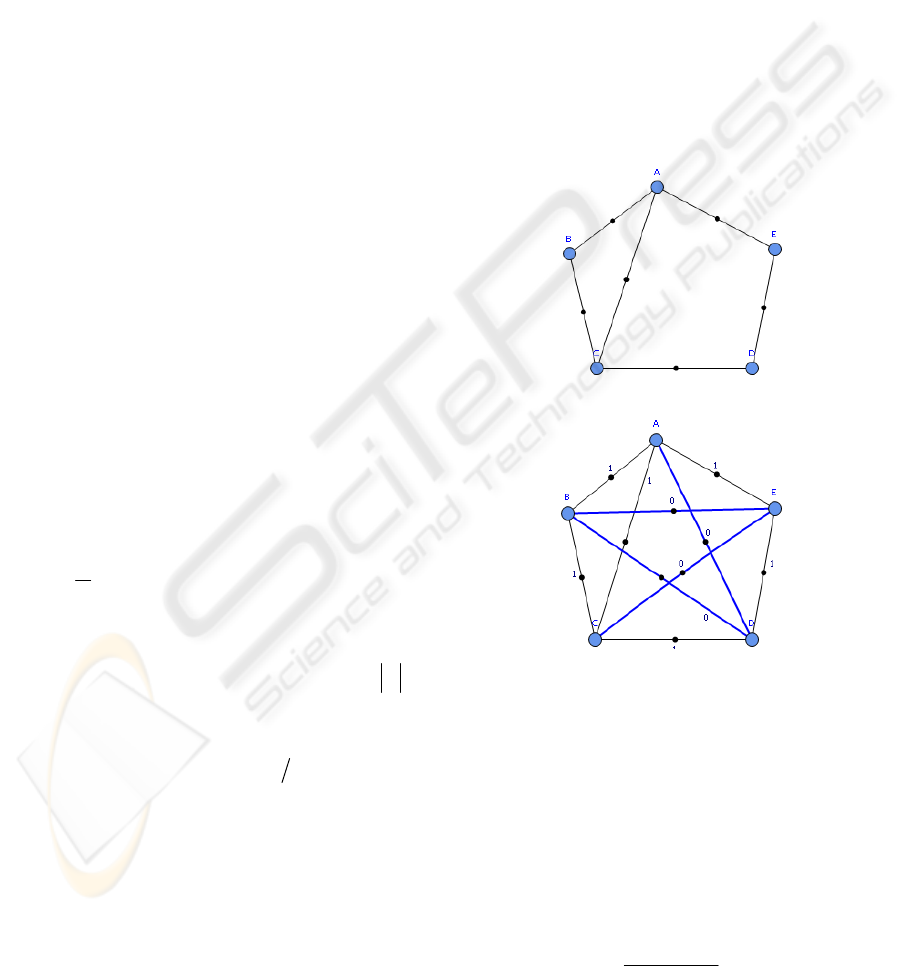
instance is an unordered vertex subset VV ⊆' .

Each ant should traverse some path across the edges

of graph to cover exactly and only the vertices in

'V , however this path may really do not exist. For

overcoming this problem, we constitute a complete

graph G

= (V , E

) including the vertex set V of G

such that every pair of vertices are connected by an

edge in E

. To aware some ant, say ant k, of

distinguishing between original and added edges in

, we define a binary connectivity function

{}

1,0: →

EC for each edge ),( ji as:

⎩

⎨

⎧

−∈

∈

EEji

Eji

jiC

),(0

),(1

),(

(1)

For a better understanding aims, we explained

our implementations on a graph with 5 vertices

which have shown in Fig. 2(a). Also, applying Eq.

(1) to it is given in Fig. 2(b). We know that this

special instance has more than one solution such as

{}

ECA ,, ,

{}

ECB ,, and so on, and so for most of

the solutions we can not find a corresponding path in

graph that covers exactly and only the solution

vertices. However, by our graph transformation the

solution paths, which can obtained in any order of

vertices, can be reached.

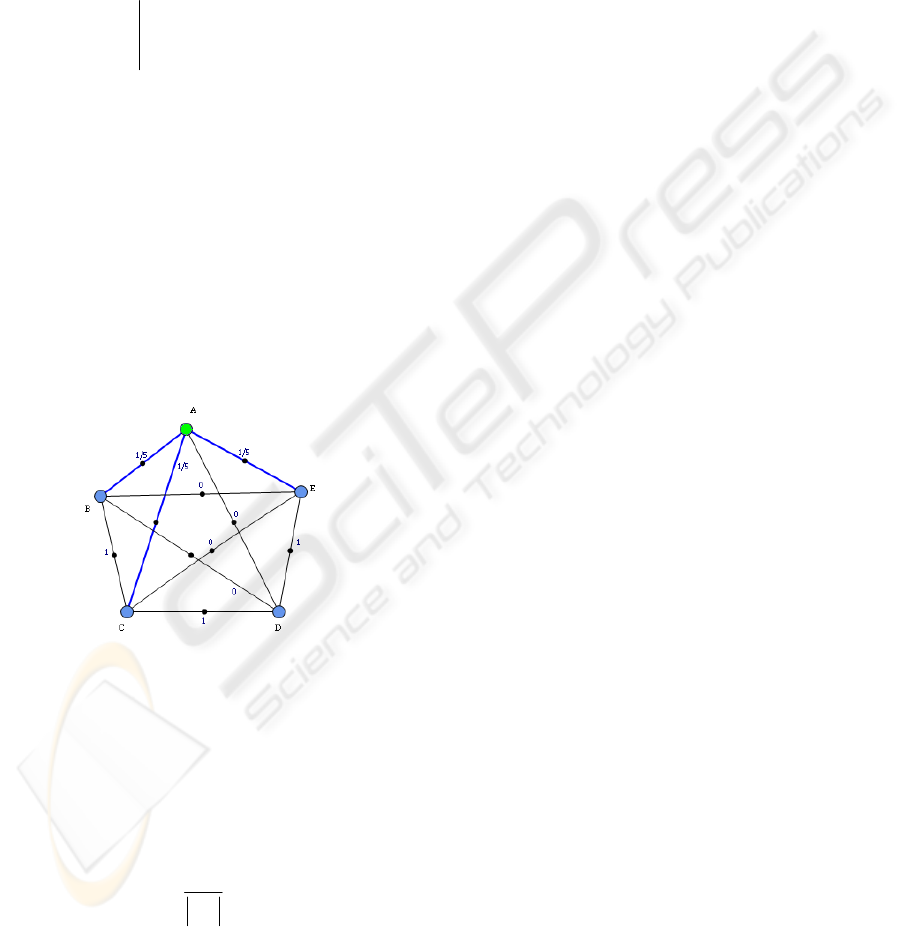
2.2 Connectivity Updating Rule

The value of an edge, connectivity value, in E is

updated when one of its edge vertices was visited by

some ant, say ant k, in the following way:

jiC

),( =

, if edge Eji ∈),( and either

vertex i or j is visited by ant k.

(2)

in which

n is the number of graph vertices, V .

Fig. 3 shows the graph of previous example in which

the connectivity values of edges

),( BA , ),( CA

and

),( EA

have been updated to 51 when vertex

is visited. The update settings according to Eq.

(2) have a twofold benefit. First, the desirability of

each vertex, as the next one to visit, can be evaluated

dynamically. To be exact, we define:

∑

∈

Ejr

jrCD

),(

(3)

as the preference number for vertex j. So, the larger

preference values the higher desirability of vertex j

for ant k. Second, since a solution to MVC is a

subset of vertices the ants may need to pass some

steps in order to complete their own tours. However,

D for all j, the ant k has completed its own

tour, a good stopping criteria. Note that, before

starting the next cycle, the connectivity values

should be reset using Eq. (1) to restore the original

graph information.

2.3 State Transition Rule

One of the main parts of an ACO-based solver,

which results the improvement in both optimality

and efficiency of the algorithm, is the state transition

rule. So we have devised an efficient pruning-based

heuristic for this phase of our ACO for MVC

problem.

(a)

(b)

Figure 2: An example. (a) The original graph instance. (b)

Illustration of our graph transformation.

Unlike the most of ACO-based solvers, that the

preference information is deposited on edges, we

(due to underlying problem characteristics)

deposited the preference information on vertices.

Our state transition rule which describes the

probability of selecting vertex j, as next vertex, for

ant k by:

∑

∈

βα

ητ

(4)

A PRUNING BASED ANT COLONY ALGORITHM FOR MINIMUM VERTEX COVER PROBLEM

283

where

A is the set of accessible vertices for ant k.

also,

and

represent the global pheromone

updating factor and local desirability scale for vertex

j, respectively. As the pruning part of Eq. (4), the ant

k is not forced to consider all of the vertices to select

the best one, vertex j. Instead, we define

V as the

visible set for ant k. In fact, we provide:

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

≥=

∑

∈

jrCjV 1),(

(5)

as the checklist for ant k and prune the other

vertices. We will show soon that this simple

heuristic of Eq. (5) results very high efficiency in

both time and solution optimality for MVC problem.

2.4 Pheromone Updating Rule

The ACO relies on the synergy among a population

of ant agents. Here, we use the global and local

pheromone updating rules as follows. First, at the

end of each cycle, the pheromone left on the vertices

of the currently best solution is reinforced. Suppose

that V'

is the currently best solution. For each vertex

Figure 3: Applying connectivity updating rule to our

running example.

Vi '∈ we will update its pheromone according to

global updating by:

iii

−= )1(

(6)

where

V '

=Δ

(7)

and

)1,0(∈

is a parameter which simulates the

evaporation rate of the pheromone intensity and

enables the ants to forget the bad decisions

previously done.

Second, we apply a local pheromone updating

rule to explore the solution space as far as possible

and permit new ants to visit the unvisited vertices

with a higher probability which leads to diversity of

the solutions obtained. This is accomplished by the

following rule:

')'1(

−

(8)

where

)1,0('

∈

is a parameter adjusting the

pheromone previously laid on vertex i and

is the

same as the initial value of pheromone laid on each

vertex before starting the algorithm. Reduction in

the pheromone intensity of the vertex i is obvious

from Eq. (8), as expected.

2.5 Stopping Criterion

The stopping criterion of an ACO could be a

maximum number of iterations, a constant CPU time

limit, or any other fixed criteria which leads to best

improvement of the algorithm. In this paper, we use

an alternative, a given number of iterations in which

no improvement on the solution is obtained.

3 EXPERIMENTAL RESULTS

In this section, we present the experimental results

obtained by MVC-AC for solving the problem.

The algorithm has been implemented by Java

programming language on windows platform and

Intel Pentium(R) 4 CPU 2.40 GHz processor. The

parameters used in our implementation are

=0.7

and

=0.3. The parameter setting for

has an

important role in the ACO algorithms. For some

fixed values of

and

, we run our algorithm

with different values of

. According to

experiences, MVC-AC with

=0.03 exhibits the

best performance for getting the optimum solution.

After that, we first, run our algorithm on regular

graphs of (Papadimitriou and Steiglitz, 1972), with

k=32 and k=66, namely "ps100" and "ps202",

respectively. We got the optimum solutions in 100

runs of MVC-AC, consistently. Our comparisons

with GENEsYs, a genetic algorithm software

package, from (Khuri and Back, 1994) and HGA of

Kotecha and Gambhava, 2003) on these graphs are

reported in Tables 1 and 2.

IJCCI 2009 - International Joint Conference on Computational Intelligence

284

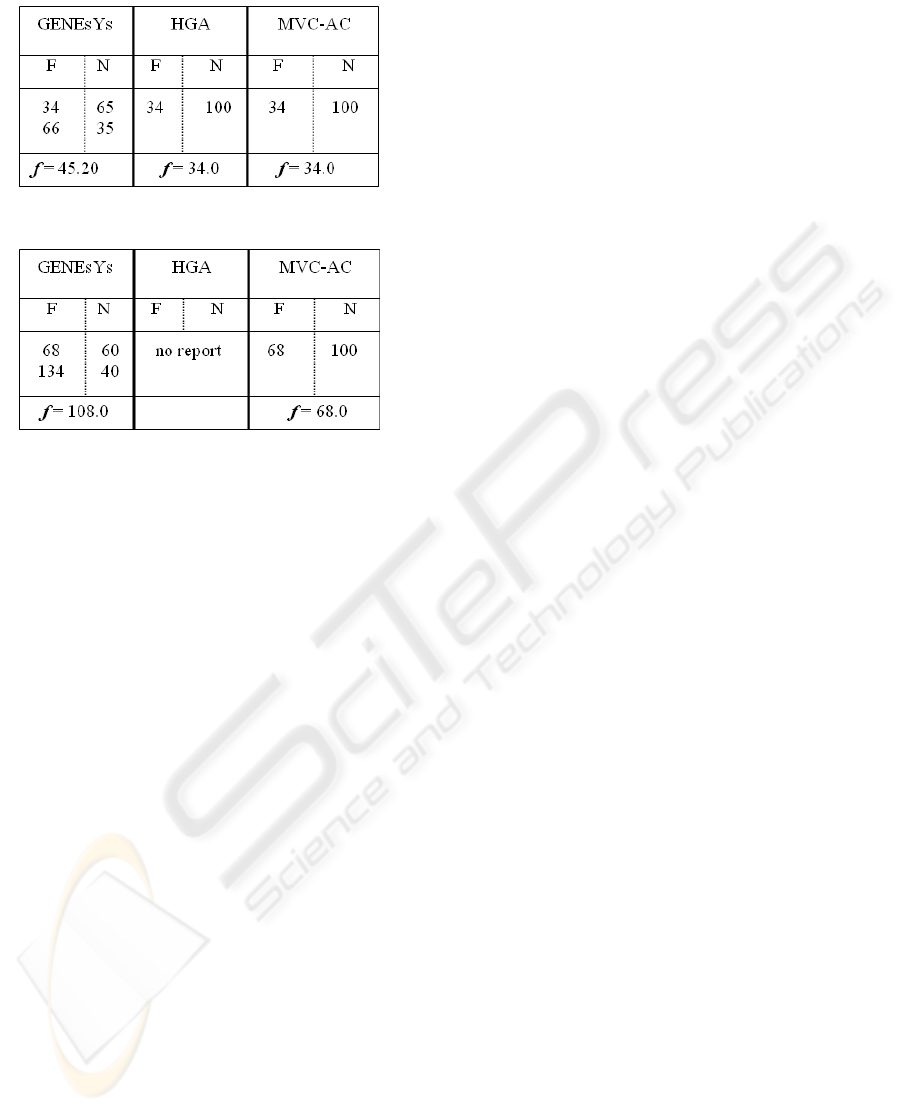
Table 1: Comparison results for "ps100" graph.

Table 2: Comparison results for "ps200" graph.

Then, we tested algorithm on more challenging

instances of random graphs which described in

(Khuri and Back, 1994). We got very surprising

results in comparison with Khuri and Back's results

(Khuri and Back, 1994) and vercov heuristic's

reported there. The results of 100 runs of MVC-AC

on "mvcp100-02", "mvcp100-03", "mvcp200-01"

and "mvcp200-02", which are more challenging,

summarized in Tables 3 and 4. According to

comparisons, MVC-AC treats very consistent and

effective for solving the minimum vertex cover

problem.

4 CONCLUSIONS

One of the most challenging problems of the graph

theory is the NP-complete minimum vertex cover

problem. In this paper, we introduced a simple but

efficient Ant Colony Optimization algorithm, called

MVC-AC, for solving this problem. Most of our

ACO components incorporate with the standard

ACO algorithms. According to ACO literature, we

speed up the ants traversal by considering a heuristic

into the state transition rule of our ACO. Also, by

introducing a new pruning based approach, the

visible set for each ant, we restricted the ant search

space only to vertices in its visible set, resulting

substantial improvement for both time and

convergence rate of the algorithm.

For experience, we compared our algorithm with

some efficient existing algorithms based on

evolutionary algorithms, such as GENEsYs and

HGA. Also a variety of benchmarks is used to test

MVC-AC. As the experimental results show, MVC-

AC not only outperforms the algorithms above, but

it also treats very efficient and consistent with for

solving the minimum vertex cover problem.

REFERENCES

D. Costa and A. Hertz, (1997), "Ants Can Color Graphs",

Journal of Operational Research Society 48, pp. 295-

305.

I. Dinur and S. Safra, (2001), "The Importance of Being

Biased", Technical Report, Department of Computer

Science, Tel Aviv University, Israel.

K. Kotecha and N. Gambhava, (2003) "A Hybrid Genetic

Algorithm for Minimum Vertex Cover Problem", In

Proc. of the 1

Indian International Conference on

Artificial Intelligence, India.

M. Dorigo, V. Maniezzo and A. Colorni, (1991), "Positive

Feedback as a Search Strategy", Technical Report, 91-

016, Politecnico idi Milano.

M. Dorigo and L. M. Gambardella, (1997), "Ant Colony

System: A Cooperative Learning Approach to the

Traveling Salesman Problem", IEEE Transactions on

Evolutionary Computation, 1(1) pp. 53-66.

M. Hifi, (1997), "A Genetic Algorithm-based Heuristic for

Solving the Weighted Maximum Independent Set and

Some Equivalent Problems", Journal of Operational

Research.

M. R. Gary and D. S. Johnson, (1979), "Computers and

Intractability: A Guide to the Theory of NP-

Completeness", San Francisco, CA: W. H. Freeman.

R. M. Karp, (1972), "Reducibility Among Combinatorial

Problems", In R. E. Miller and J. W. Theater (eds),

Complexity of Computer Computations, New York:

Plenum Press, 1972.

S. Khuri and Th. Bäck, (1994), "An Evolutionary

Heuristic for the Minimum Vertex Cover Problem", J.

Hopf., editor: Genetic Algorithms within the

Framework of Evolutionary Computation, pp. 86-90,

Max Plank Institut fur Informatic, Saarbrucken.

S. Mehrabi, A. Mehrabi and A. D. Mehrabi, (2009), "A

New Hybrid Genetic Algorithm for Maximum

Independent Set Problem", In Proceedings of the 4

International Conference on Software and Data

Technologies (ICSOFT'09), Sofia, Bulgaria.

S. Mehrabi and A. Mehrabi, (2009), "A New Genetic

Algorithm for Multiprocessor Scheduling Problem" (in

Persian), In Proceedings of the First National

Conference on Software Engineering (NSEC'09), pp.

127-132. Tehran, Iran.

C. H. Papadimitriou and K. Steiglitz, (1982),

"Combinatorial Optimization: Algorithms and

Complexity", Prentice Hall.

C. H. Papadimitriou, (1994), "Computational

Complexity", Addison Wesley, Reading, MA.

D. B. West, (2001), "Introduction to Graph Theory",

Prentice Hall, Inc.

A PRUNING BASED ANT COLONY ALGORITHM FOR MINIMUM VERTEX COVER PROBLEM

285

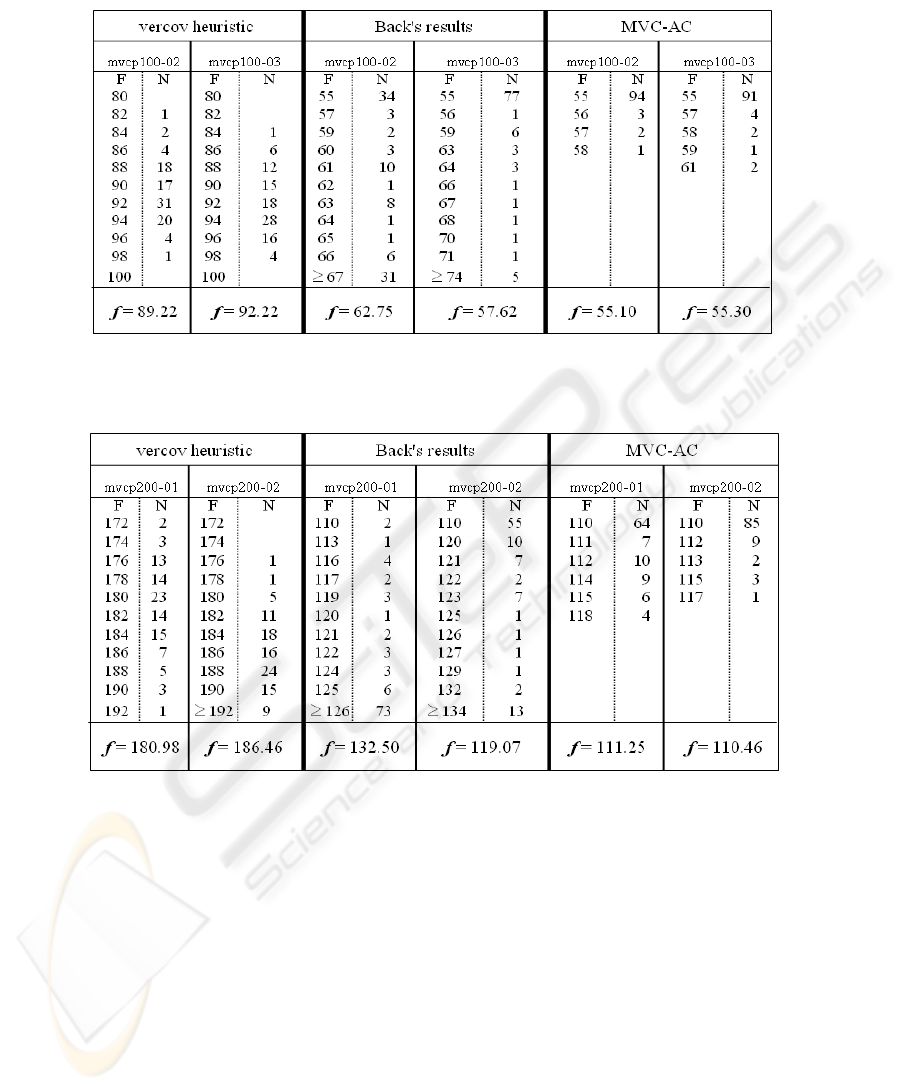
Table 3: The comparison of vercov heuristic and Back's results with MVC-AC results on "mvcp100-02" and "mvcp100-03"

random graph instances.

Table 4: The comparison of vercov heuristic and Back's results with MVC-AC results on "mvcp200-01" and "mvcp200-02"

random graph instances.

IJCCI 2009 - International Joint Conference on Computational Intelligence

286