MULTIPARTY COMPARISON
An Improved Multiparty Protocol for Comparison of Secret-shared Values
Tord Ingolf Reistad
Department of Telematics, O.S. Bragstads plass 2B, NTNU, Trondheim, Norway
Keywords:
Multiparty, Secret sharing, Comparison, Information hiding.
Abstract:
Given any linear secret sharing scheme with a multiplication protocol, we show that a set of players holding
shares of two values a,b ∈Z
p
for some prime p (written [a] and [b]), it is possible to compute a sharing [result]
such that [result] = ([a] < [b]). The protocol maintains the same security against active/adaptive adversaries
as the underlying secret sharing scheme.
1 INTRODUCTION
In the millionaire problem (Yao, 1982) two or more
millionaires want to know which one of them is richer
without revealing each other’s wealth. This was one
of the first protocols for multiparty computation, and
illustrates the challenges in multiparty protocols in
practical applications. As the goal of the protocol be-
tween the millionaires should not only keep the input
private, but also compute the result quickly.
In the millionaire problem each player (million-
aire) knows his own wealth, which is the input to that
is sent to the protocol. In a more generalized setting
the inputs might not be explicitly known to any sin-
gle party, but resulting from a linear combination of
secret inputs by several parties, or from an earlier in-
termediate result.
In general a multiparty computation (MPC) is a
computation between a number of parties P
1
,...,P
n
.
These parties have private inputs x
1
,...,x
n
and they
want to compute some function f on these inputs,
where f(x
1
,...,x
n
) = (y
1
,...,y
n
) such that P
i
learns
y
i
but nothing else. The players are mutually mis-
trusting and do not wish to share their inputs.
When considering concrete applications, the func-
tion f is often computed using Shamir secret shar-
ing scheme over a field Z
p
for some large odd prime
p. The function is computed using simulated integer
arithmetic. This means that although the values are
points in a finite field, they can be used as integer val-
ues in Z. This is analogous to current day computers
where each value is stored as a limited set of bits. The
difference is that in the multiparty protocol there is no
way to efficiently check for overflow, the prime p will
therefore have to be chosen such that all simulated in-
teger values are less than p for all possible inputs.
Although there exists efficient protocols for addi-
tion and multiplication of secret shared values, most
functions or algorithms f require additional operators
such as comparison and equality checking. This moti-
vates us in constructing specialized efficient protocols
that realizes such operators. These operatorprimitives
may be used repeatedly and any improvement in the
implementations of the primitive operators will lead
to a similar improvement in an overall application.
Comparison in a multiparty computation setting
could be solved by circuit based computations. All
inputs would then be split into bits. Comparison be-
tween inputs would then be easy, but this would make
addition and multiplication much more complicated
so the overall effect would be slower computer pro-
grams.
This work describes a protocol for one such primi-
tive operator, namely comparison (inequality-testing)
of secret shared values. That is, given two secret
shared values [a] and [b], a secret shared bit [result] =
[a < b] is obtained stating whether one value is larger
than the other without leaking any information. This
protocol is more efficient than all previously pub-
lished constant round protocols for comparison.
Section 2 discusses this work in relation to previ-
ously published papers. Sections 3 and 4 introduce
the model as well as a number of primitives required.
Most of these are well-known, and are included in or-
der to provide detailed analysis of our protocol. Sec-
tion 5 Gives first a high-level view of the protocol and
then discusses the details. Finally Section 6 gives the
325
Ingolf Reistad T. (2009).
MULTIPARTY COMPARISON - An Improved Multiparty Protocol for Comparison of Secret-shared Values.
In Proceedings of the Inter national Conference on Security and Cryptography, pages 325-330
DOI: 10.5220/0002233603250330
Copyright
c
 SciTePress

conclusion and further improvements.
2 RELATED WORK
Research on multiparty computation (MPC) has
mostly focused on either primitives for multiparty
computations or on some concrete applications such
as actions (Bogetoft et al., 2005; Fischlin, 2001;
Schoenmakers and Tuyls, 2004). This paper consid-
ers neither of these cases. It assumes underlying prim-
itives for multiparty computations with addition and
multiplication of field elements. It also does not con-
sider concrete applications as comparison of elements
are just one piece in a framework for multiparty com-
putations.
Damg˚ard et al. provided the first constant rounds
comparison in the present setting (Damg˚ard et al.,
2006), the protocol relied on bit-decomposition of
values this approach required O (ℓlog(ℓ)) secure mul-
tiplications where ℓ = log(p). Comparison was later
improved by Nishide and Ohta (Nishide and Ohta,
2007) who reduced the complexity to O (ℓ) multipli-
cations.
The most recent solutions have concentrated on a
binary representation of the values being compared.
Thus, unless a radically different approach is taken,
improving on the O (ℓ) bound does not seem feasi-
ble. The present work builds on sub-protocols and
ideas of (Damg˚ard et al., 2006), (Nishide and Ohta,
2007) and (Reistad and Toft, 2007) and aims at re-
ducing the constants hidden under big-O . These costs
hidden under big-O are becoming more relevant as
multiparty is implemented and used in practical ap-
plications (Bogetoft et al., 2008).
Table 1 compares the solution presented in this pa-
per to those of Damg˚ard et al., Nishide and Ohta, and
Reistad and Toft. Type A refers to comparison of ar-
bitrary values [a],[b] ∈ Z
p
, while R is for restricted
values [a],[b] < ⌊
p
4
⌋ and a prime p = 2
ℓ
−c where
c is a small integer; when using Z
p
to simulate in-
teger computation, it is not unreasonable to choose
p in such a way to accommodate these two assump-
tion. Furthermore to give the protocols equal footing
we assume that all protocols use the same underlying
protocols see section 4. E.g. the protocol for creating
random bitwise shared values are created using the
same protocol. For comparison of arbitrary values in
arbitrary fields it is assumed that the underlying pro-
tocol will have to be run two times for a total of 8ℓ
multiplications. For a well chosen p and restricted
values this complexity can be assumed to be close to
2ℓ. As the test becomes more efficient and the prob-
ability of having to run the underlying protocol twice
becomes insignificant.
A distinction is also made between online
complexity and pre-processing complexity. Pre-
processing are all the computations that can be made
independent of the private inputs. Online computa-
tions are all those computations that can only be made
once the private inputs are available.
3 MODEL
We assume a linear secret sharing scheme that allows
for multiparty addition and a multiplication of secret
shared values, to be shared among n > 2 parties. The
security properties of the secret sharing scheme are
inherited, i.e. if the secret sharing scheme is uncon-
ditionally secure against active/adaptive adversaries
then so is the protocols proposed. As as example,
consider Shamir’s scheme along with the protocols of
Ben-Or et al. (or the improved protocols of Gennaro
et al.) (Shamir, 1979; Ben-Or et al., 1988; Gennaro
et al., 1998).
The communication model is that there exist au-
thenticated private channels between each pair of par-
ties. The model assumes that in addition to sharing
values and performing secure arithmetic on Z
p
, the
parties may reveal (reconstruct) shared values. Re-
vealing a secret shared value ensures that the value
becomes known by all parties.
We use [a] to denote a secret sharing of a ∈ Z
p
among the n parties, where p is an ℓ-bit prime (ℓ > 7).
The operators are written using an infix notation. For
shared values [a] and [b], and constant c ∈Z
p
, compu-
tation of sums will be written as [a] + c and [a] + [b],
while products will be written c[a] and [a][b]. The first
three operator are computed locally, while the fourth
operator represents an invocation of the multiplication
protocol.
Sharings of bits, [b] ∈ {0, 1} ⊂ Z
p
will also be
considered. Boolean arithmetic is written using in-
fix notation, though it must be realized using field
arithmetic. Notably xor of two bits is constructed as
[b
1
]⊕[b
2
] = [b
1
]+[b
2
]−2[b
1
][b
2
] which is equivalent.
Values may also be bitwise shared, written [a]
B
.
Rather than having a sharing of a value itself, [a],
sharings of the bits of the binary representation of a
are given, i.e. [a
0
],...,[a
ℓ−1
] ∈{0,1} such that
[a]
B
=
ℓ−1
∑
i=0
2
i
[a
i
] (1)
for ℓ = ⌈log(p)⌉, with the sum being viewed as
occurring over the integers. Note that [a] is easily ob-
tained from [a]
B
as it is a linear combination.
SECRYPT 2009 - International Conference on Security and Cryptography
326

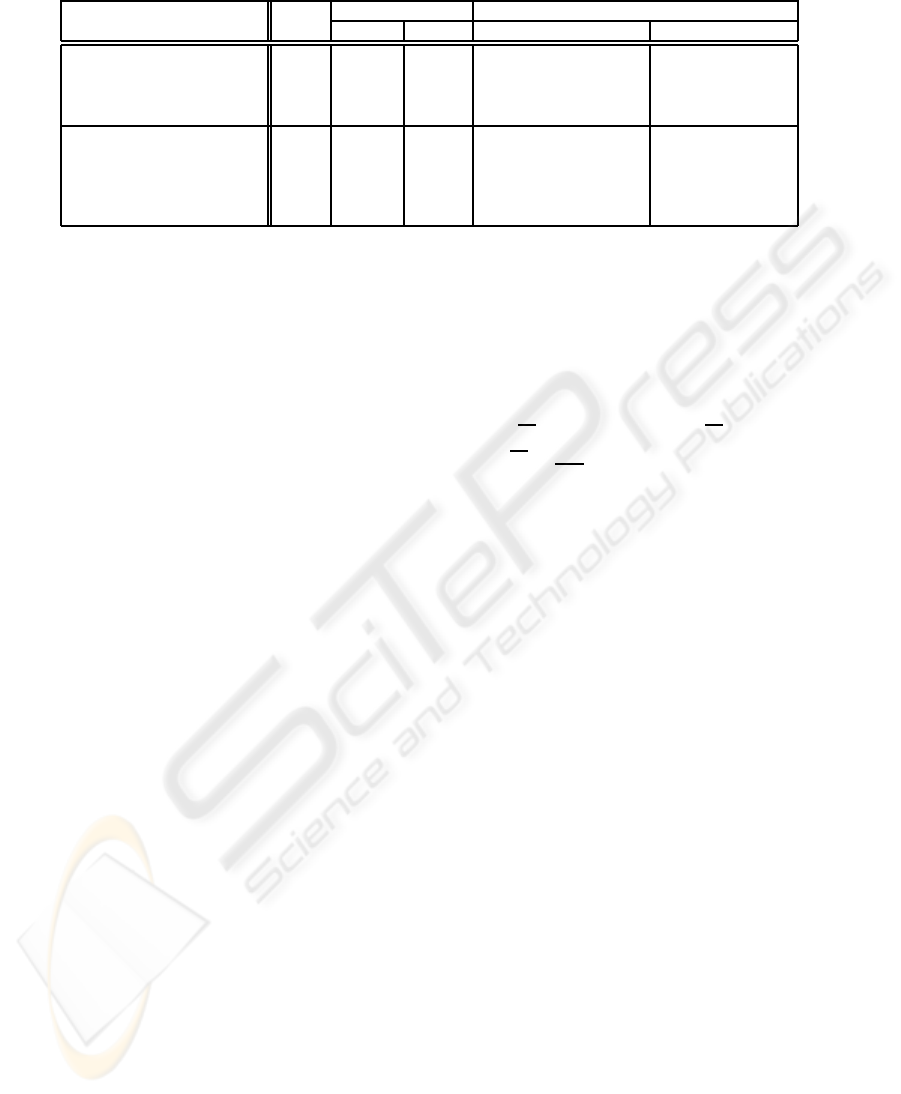
Table 1: Complexities of comparison protocols.
Presented in Type Rounds Multiplications
overall online overall online
(Damg˚ard et al., 2006) A 44 37 184ℓlog
2
(ℓ) + 209ℓ 21ℓ+ 56ℓlog
2
(ℓ)
(Nishide and Ohta, 2007) A 15 8 279ℓ+ 5 15ℓ+ 5
(Reistad and Toft, 2007) A 12 4 84ℓ+ 78log
2
(ℓ) + 17 18l + 5
This paper A 8 2 58.5ℓ+ 33 4.5ℓ
(Damg˚ard et al., 2006) R 44 37 184ℓlog
2
(ℓ) + 165ℓ 21ℓ+ 56ℓlog
2
(ℓ)
(Nishide and Ohta, 2007) R 13 6 49ℓ + 5 5ℓ + 1
(Reistad and Toft, 2007) R 10 2 17ℓ+ 26log
2
(ℓ) + 4 5ℓ
(Reistad and Toft, 2007) R 8 2 20ℓ+ 36log
2
(ℓ) + 6 5ℓ
This paper R 6 1,5 7,5ℓ + 11 1,5ℓ
Similarly a publicly known value c can be split
into bits, where c
i
represents the i’th bit of c. c
0
is the
least significant bit of c.
Complexity. When considering complexity, the fo-
cus of the analysis will be on communication. Simi-
lar to other work, focus will be placed on the number
of invocations of the multiplication protocol as this is
considered the most costly of the primitives. It is as-
sumed that invocations of the multiplication protocol
parallelize and multiplications are executed in parallel
when possible. When we say ”one round” we mean
one round of arbitrary many invocations of the mul-
tiplication protocol, all performed in parallel among
the parties.
Multiplication by constants and addition require
no interaction and is therefore considered cost-less.
The complexity of sharing and revealing is seen as
negligible compared to that of multiplication. Rounds
for reconstruction are disregarded as in other work.
4 SIMPLE PRIMITIVES
This section introduces a number of simple primitives
required below. Most of these sub-protocols are given
in (Damg˚ard et al., 2006) but are repeated here in or-
der to provide a detailed analysis as well as for com-
pleteness. Most of these are related to the generation
of random values unknown to all parties. It is impor-
tant to note that these may fail, however, this does not
compromise the privacy of the inputs – failure sim-
ply refers to the inability to generate a proper random
value (which is detected). Generally the probability
of failure will be of the order 1/p, which for simplic-
ity will be considered negligible, see (Damg˚ard et al.,
2006) for further discussion.
Random Element Generation. A sharing of a uni-
formly random, unknown value [r] may be generated
by letting each party share a uniformly random value
r
i
∈ Z
p
. The sum [r] =
∑
r
i
mod p of these is uni-
formly random and unknown to all, even in the face
of an active adversary. The complexity of this is as-
sumed to be equivalent to one invocation of the mul-
tiplication protocol.
Random Bits. The parties may create a uniformly
random bit [b] ∈ {0,1}. The parties may generate
a random value [r] and reveal its square, r
2
. If this
is 0 the protocol fails, otherwise they compute [b] =
2
−1
((
√
r
2
)
−1
)[r] + 1) where
√
r
2
is defined such that
0 ≤
√
r
2
≤
p−1
2
. The complexity is two multiplica-
tions in two rounds.
Creating Random Bitwise Shared Values. The
parties may create a uniformly random bitwise shared
value [r]
B
less than some m, k = ⌈log
2
(m)⌉, as de-
scribed in (Reistad and Toft, 2007). This is accom-
plished by generating k bits [r
k−1
],...,[r
0
] and verify-
ing that this represents a value less than m. The ver-
ification is done by creating a vector with elements
[e
i
] and revealing them. Note that this protocol will
be used to generate uniformly random bitwise shared
elements of Z
p
(done by setting m = p).
[e
i
] = [s
i
]

1+(m−1)
i
−[r
i
]+
k−1
∑
j=i+1
((m−1)
j
⊕[r
j
])

(2)
The notation (m−1)
i
denotes the i’th bit of m−1
and [s
i
] are random shares in Z
p
. Revealing the shares
[e
i
] gives a vector that will contain a 0 element only
when m −1 < [r]
B
⇔ [r]
B
≥ m for proof see (Reis-
tad and Toft, 2007). Note that this protocol will leak
information about the individual bits [r
i
] if there is a
0 element, but this coincides with discarding the bits
[r
i
].
The complexity of generating random bitwise
shared values consists of the generation of the k bits
and k masks, in addition there are needed k multipli-
cations to perform the masking. Overall this amounts
to 4k multiplications in three rounds as the [r
i
] and [s
i
]
may be generated in parallel. For added efficiency the
[e
i
] where (m−1)
i
= 1 do not need to be calculated or
revealed, as they are guaranteed to be non-zero. For
MULTIPARTY COMPARISON - An Improved Multiparty Protocol for Comparison of Secret-shared Values
327

m = 2
k
−c, where c is a small integer the complexity
can be reduced to 2k+ 2log(c).
Additional Improvement. The probability that the
protocol above fails to return a bitwise secret shared
value, depends upon m. The worst case scenario is
m = 2
k
+ 1, which makes the probability of failing
equal to 1/2. For 5 additional multiplications and no
extra rounds the probability of restarting can be low-
ered to an upper bound of 1/4 for all m. This is done
by noting that if the two highest order bits of m are
10, then the protocol fails if the products of the two
highest bits of [r]
B
is 1. The solution is therefore to
create 2 or sets of candidates for highest order bits.
The two bits in each of the candidates can be mul-
tiplied together and revealed, and the candidate only
used if the product is 0. This introduces no additional
rounds of communication as [t
k−1
t
k−2
] can be com-
puted in parallel with computing the bits.
[r
k−1
r
k−2
] = 4
−1
(
[t
k−1
t
k−2
]
q
t
2
k−1
q
t
2
k−2
+
[t
k−1
]
q
t
2
k−1
+
[t
k−2
]
q
t
2
k−2
+1)
(3)
Unbounded Fan-in Multiplications. It is possible
to compute prefix-products of arbitrarily many non-
zero values in constant rounds using the method of
Bar-Ilan and Beaver (Bar-Ilan and Beaver, 1989).
Given [a
1
],...,[a
k
] ∈ Z
∗
p
, [a
1,i
] = [
∏
i
j=1
a
j
] may be
computed for i ∈ {1,2,...,k} as follows.
Let u
0
= 1 and generate k random non-zero values
[u
1
],...,[u
k
], however, in parallel with the multipli-
cation of [u
j
] and its mask [v
j
], compute [u
j− 1
v
j
] as
well. Then [u
j− 1
u
−1
j
] may be computed at no cost as
[u
j− 1
v
j
] ·(u
j
v
j
)
−1
. Each [a
j
] is then multiplied onto
[u
j− 1
u
−1
j
] and all these are revealed. We then have:
[a
1,i
] =
i
∏
j=1
(a
j
u
j− 1
u
−1
j
) ·[u
i
] (4)
Privacy of the [a
j
] is ensured as they are masked
by the [u
−1
j
], and complexity is 5k multiplications in
three rounds. Regarding the preparation of the mask-
ing values as pre-processing, the online complexity is
k multiplications in a single round.
5 THE COMPARISON
PROTOCOL
The comparison protocol consists of 3 sub proto-
cols, the first sub-protocol transforms the comparison
[a] < [b] into a comparison [r]
B
> c, where [r]
B
is a
random secret shared value and c is a value known to
all parties. This transformation is done so the other
two protocols can work on individual bits.
The second sub-protocol transforms the compari-
son [r]
B
> c into a single [x] this share [x] is made in
such a way that [x] <
√
4p for all [r]
B
and c and the
least significant bit of [x] is equal to the result of the
comparison test between [r] and c.
The third sub-protocol extracts the least signifi-
cant bit of [x] <
√
4p efficiently. Once the least signif-
icant bit of [x] is extracted then the bit representing the
answer to the original comparison between [a] < [b] is
computed with two xor’s.
5.1 First Transformation
When [a],[b] <
p−1
2
and [z] = [a] −[b], then [a] < [b]
is equivalent to determining the least significant bit of
2[z], written [(2z)
0
]. The least significant bit of [(2z)
0
]
is found by computing and revealing c, where
[c] = 2[z] + [r]
B
= 2([a] −[b]) + [r]
B
(5)
c
0
is the least significant bit of c, [r
0
] is the least sig-
nificant bit of [r]
B
and [r]
B
is a random bitwise shared
value. We then have the following equation:

[a] < [b]

= [(2z)
0
] = c
0
⊕[r
0
] ⊕

[r]
B
> c

(6)
With this first transformation the comparison be-
tween [a] and [b] has then been transformed to the
problem of comparing [r]
B
> c. For more detail on
the transformation see (Reistad and Toft, 2007), and
for unbounded values of [a] and [b] see (Nishide and
Ohta, 2007).
The cost of this transformation is the creation of
one secret shared value and one secret shared xor. The
calculation of the secret shared value can be done in
3 rounds in parallel with other pre-processing and the
xor adds one online multiplication in one round.
Privacy follows from the security of the secret
sharing scheme. Revealing c does not leak informa-
tion, because [r]
B
is a uniformly random secret shared
value. Thereforethe distribution of c is also uniformly
random.
5.2 Computing X
Theorem 1. Given a random secret shared value
[r]
B
and a publicly known value c. Let the secret
shared value [x] be constructed as:
[x] =
l−1
∑
i=0
[r
i
](1−c
i
)2
∑
l−1
j=i+1
c
j
⊕[r
j
]
(7)
The least significant bit of [x], written [x
0
] is equal
to the value [r
i
], where i is the most significant bit
where [r
i
] 6= c
i
. Or in other words [x
0
] is equal to the
boolean statement ([r]
B
> c).
SECRYPT 2009 - International Conference on Security and Cryptography
328

Proof. Starting from the most significant bits we see
that [r
i
](1−c
i
) and the sum
∑
l−1
j=i+1
c
j
⊕[r
j
] are 0, as
long as [r
i
] = c
i
. Beginning with the highest order
bit where [r
i
] 6= c
i
, the expression [r
i
](1−c
i
) is equal
to [r
i
]. For lower order bits after the first one where
[r
i
] 6= c
i
, the sum
∑
l−1
j=i+1
c
j
⊕[r
j
] becomes non-zero.
Therefore all lower terms except the first one where
[r
i
] 6= c
i
become either. 0 or some value 2
k
, where
k < 1. 
For the greatest efficiency an even more complex
form for the function for [x] will be used. The function
[x] is essentially the same only that for each summa-
tion not one but two bits of [r
i
] and c
i
are considered at
the same time. Therefore [r
i
](1−c
i
) will be expressed
as r
i
> c
i
for 2 bits at a time, and c
j
⊕[r
j
] will only
return 1 if both pair of bits are equal. This ensures
that [x] < 2
l+1
2
.
This functions which compares two bits at a time
is more efficient. In addition it also avoids a problem
in the next protocol. As that the function [x] as stated
above has a worst case bit length of ℓ.
In the 2-bit version each pair of secret shared bits
have to be multiplied together at a cost of 0,5ℓ mul-
tiplications. This also computes the two bit version
of [r
i
](1−c
i
) and c
j
⊕[r
j
]. Computing 2
∑
l−1
j=i+1
c
j
⊕[r
j
]
can be done with fan-in multiplications in 2,5ℓ multi-
plications and the final multiplication costs 0,5ℓ. The
protocol therefore takes a total of 3, 5ℓ multiplications
and 3 rounds (as the random values for fan-in multi-
plications can be done in pre-processing). Privacy of
computing [x] is immediate as no value is revealed.
5.3 Extracting the Least Significant Bit
Extracting the last bit of a secret shared value [x],
where [x] <
√
4p, can be done efficiently. First a
bitwise secret shared random variable [s]
B
is created.
The the value d is calculated and revealed, where
[d] = [s]
B
+ [x] (8)
From this we can easily see that the least signifi-
cant bit of [x], written as [x
0
] is equal to [s
0
]⊕d
0
, when
d >
√
4p.
To create a generalized version for finding [x
0
],
[s]
B
will have to be split into 3 parts [s]
B
=
2
l−1
[s
l−1
]+ 2
l−2
[s
l−2
]+ [ ˆs]
B
. Note that two bits of in-
formation are needed from [s]
B
as in a worst case sce-
nario p might be 2
l−1
+ 1 and [s]
B
might be 2
l−1
−1.
We then have that [ˆs]
B
+[x] < 2
l−2
+
√
4p < p, for
all p. As [
ˆ
d] = [ ˆs]
B
+ [x] never will need a modulo p
reduction.
[x
0
] = [ ˆs
0
]
B
⊕[
ˆ
d
0
] (9)
The value [
ˆ
d
0
] cannot be revealed, as this would
leak information about [x], on the other hand there are
only 4 possible values for [
ˆ
d] based upon the value d,
and the shares [s
l−1
] and [s
l−2
]. Therefore following
equation need only one secret shared multiplication to
compute [
ˆ
d
0
]: (Note (d < 2
l−1
) returns 1 if d < 2
l−1
).
[
ˆ
d
0
] =(1 −[s
l−1
] −[s
l−2
] + [s
l−1
s
l−2
])d
0
+ ([s
l−2
] −[s
l−1
s
l−2
])(d
0
⊕(d < 2
l−2
))
+ ([s
l−1
] −[s
l−1
s
l−2
])(d
0
⊕(d < 2
l−1
))
+ ([s
l−1
s
l−2
])(d
0
⊕(d < (2
l−1
+ 2
l−2
))
Going from [
ˆ
d
0
] to [x
0
] adds one multiplication,
and going from [x
0
] to [[a] < [b]] also add one more
multiplication. Therefore once d is known it takes
3 multiplications in 2 rounds to compute the original
comparison. To save rounds all combinations of the
secret shared values [s
l−1
], [s
l−2
], [s
0
] and [r
0
] can be
pre-computed once [r]
B
and [s]
B
are known. This is
done with 11 multiplications and 2 rounds that run
in parallel with previous computations. The privacy
argument is the same as for the first transformation.
6 CONCLUSIONS AND FURTHER
WORK
We have presented a protocol for comparison in con-
stant rounds that is significantly faster than previous
versions. As the most time consuming part of a MPC
program is in many cases the comparison protocol,
the efficiency of the comparison protocol will directly
affect the speed of the program.
The comparison protocol in (Reistad and Toft,
2007) has be implemented in the VIFF framework
(http://viff.dk/) therefore the implementation of the
protocol in this paper will show in practice how ef-
ficient the two protocols are compared to each other.
Further improvements in the online computation
can also be done as the computation of 2
∑
l−1
j=i+1
c
j
⊕[r
j
]
when computing [x] in equation 7 can be split into
three multiplications.
•
∏
l−1
j=i+1
(1+ [r
j
]) can be pre-processed.
•
∏
l−1
j=i+1
(1 + c
j
) can be computed online without
multiparty multiplications.
• The last that product
∏
l−1
j=i+1
(1 −3 ·4
−1
(c
j
[r
j
]))
can be pre-computed in such two shares are cre-
ated and only one of them is opened depending
upon c
j
.
This will result in the same amount of pre-
computations, but will not require any online com-
putations only revealing values.
MULTIPARTY COMPARISON - An Improved Multiparty Protocol for Comparison of Secret-shared Values
329

ACKNOWLEDGEMENTS
The author would like to thank the anonymous re-
viewers for their comments, Stig Frode Mjølsnes and
Harald Øverby for useful discussions on the article
and Tomas Toft for comments and fruitful discussions
about MPC comparison.
REFERENCES
Bar-Ilan, J. and Beaver, D. (1989). Non-cryptographic fault-
tolerant computing in a constant number of rounds of
interaction. In Rudnicki, P., editor, Proceedings of the
eighth annual ACM Symposium on Principles of dis-
tributed computing, pages 201–209, New York. ACM
Press.
Ben-Or, M., Goldwasser, S., and Wigderson, A. (1988).
Completeness theorems for noncryptographic fault-
tolerant distributed computations. In 20th Annual
ACM Symposium on Theory of Computing, pages 1–
10. ACM Press.
Bogetoft, P., Christensen, D., D˚amgard, I., Geisler, M.,
Jakobsen, T., Krøigaard, M., Nielsen, J., Nielsen, J.,
Nielsen, K., Pagter, J., Schwartzbach, M., and Toft, T.
(2008). Multi-party computation goes live. Cryptol-
ogy ePrint Archive, Report 2008/068.
Bogetoft, P., Damg˚ard, I., Jakobsen, T., Nielsen, K., Pagter,
J., and Toft, T. (2005). Secure computing, economy,
and trust: A generic solution for secure auctions with
real-world applications. BRICS Report Series RS-05-
18, BRICS. http://www.brics.dk/RS/05/18/ .
Damg˚ard, I., Fitzi, M., Kiltz, E., Nielsen, J., and Toft,
T. (2006). Unconditionally secure constant-rounds
multi-party computation for equality, comparison, bits
and exponentiation. In Halevi, S. and Rabin, T., edi-
tors, Theory of Cryptography, volume 3876 of Lecture
Notes in Computer Science (LNCS), pages 285–304.
Springer.
Fischlin, M. (2001). A cost-effective pay-per-multiplication
comparison method for millionaires. In Naccache, D.,
editor, Topics in Cryptology – CT-RSA 2001, volume
2020 of Lecture Notes in Computer Science, pages
457–471. Springer-Verlag, Berlin, Germany.
Gennaro, R., Rabin, M., and Rabin, T. (1998). Simplified
vss and fast-track multiparty computations with appli-
cations to threshold cryptography. In PODC ’98: Pro-
ceedings of the seventeenth annual ACM symposium
on Principles of distributed computing, pages 101–
111, New York, NY, USA. ACM Press.
Nishide, T. and Ohta, K. (2007). Multiparty computa-
tion for interval, equality, and comparison without
bit-decomposition protocol. In PKC 2007 Interna-
tional Workshop on Theory and Practice in Public Key
Cryptography, Lecture Notes in Computer Science.
Springer-Verlag, Berlin, Germany.
Reistad, T. and Toft, T. (2007). Secret sharing compari-
son by transformation and rotation. In Preproceedings
ICITS, International Conference on Information The-
oretic Security 2007
Schoenmakers, B. and Tuyls, P. (2004). Practical two-
party computation based on the conditional gate. In
Lee, P. J., editor, Advances in Cryptology – ASI-
ACRYPT 2004, volume 3329 of Lecture Notes in
Computer Science, pages 119–136. Springer-Verlag,
Berlin, Germany.
Shamir, A. (1979). How to share a secret. Communications
of the ACM, 22(11):612–613.
Yao, A. (1982). Protocols for secure computation. In Pro-
ceedings of the twenty-third annual IEEE Symposium
on Foundations of Computer Science, pages 160–164.
IEEE Computer Society.
SECRYPT 2009 - International Conference on Security and Cryptography
330