PASSIVITY-BASED DYNAMIC BIPEDAL WALKING WITH

TERRAIN ADAPTABILITY

Dynamics, Control and Robotic Applications

Qining Wang, Long Wang, Jinying Zhu, Yan Huang and Guangming Xie

Intelligent Control Laboratory, College of Engineering, Peking University, Beijing 100871, China

Keywords:

Passive dynamic walking, Bipedal robots, Terrain adaptability, Modeling.

Abstract:

This paper presents an approach for passivity-based bipedal robots to achieve stable walking on uneven terrain.

A powered two-dimensional seven-link walking model with ﬂat feet and compliant ankles has been proposed to

analyze and simulate the walking dynamics. We further describe an optimization based control method, which

uses optimized hip actuation and ankle compliance as control parameters of bipedal walking. Satisfactory

results of simulations and real robot experiments show that the passivity-based walker can achieve stable

bipedal walking with larger ground disturbance by the proposed method in view of stability and efﬁciency.

1 INTRODUCTION

Stability guaranteed dynamic bipedal walking is one

of the keys but also one of the more challenging com-

ponents of humanoid robot design. Several actively

controlled bipedal robots are able to deal with such

dynamic stability when walk on irregular surface (Ya-

maguchi and Takanishi, 1997), step over obstacles

(Guan et al., 2006), climb stairs (Michel et al., 2007),

even if achieve bipedal running (Honda Motor, 2005).

However, to increase the autonomy of the robot, the

locomotion efﬁciency, which is far from that of hu-

man motion, has to be improved.

As one of the possible explanations for the ef-

ﬁciency of the human gait, passive dynamic walk-

ing (McGeer, 1990) showed that a mechanism with

two legs can be constructed so as to descend a gentle

slope with no actuation and no active control. Sev-

eral studies reported that these kinds of walking ma-

chines work with reasonable stability over a range of

slopes (e.g. (McGeer, 1990), (Collins et al. 2001))

and on level ground with kinds of actuation added

(e.g. (Collins et al. 2005), (Wisse et al., 2007)) show

a remarkable resemblance to the human gait. In spite

of having high energetic efﬁciency, passivity-based

walkers have limits to achieve adaptive locomotion on

rough terrain, which is one of the most important ad-

vantages of the legged robots. In addition, these walk-

ers are sensitive to the initial conditions of walking.

To overcome such disadvantages, several studies

proposed quasi-passive dynamic walking methods,

which implement simple control schemes and actua-

tors supplementarily to handle ground disturbances.

For example, (Schuitema et al., 2005) described a

reinforcement learning based controller and showed

that the walker with such controller can maximally

overcome −10mm ground disturbance. (Tedrake et

al., 2004) presented a robot with a minimal number

of degrees of freedom which is still capable of stable

dynamic walking even on level ground and even up

a small slope. (Wang et al., 2006) designed a learn-

ing controller for a two-dimensional biped model with

two rigid legs and curved feet to walk on uneven

surface that monotonically increases from 12mm to

40mm with a 2mm interval. In these studies, passivity-

based walkers are often modeled with point feet or

round feet. And the control parameter only includes

hip actuation. None of them analyzed the stability or

adaptability in quasi-passive dynamic walking with

ﬂat feet and ankle joint compliance which is more

close to human motion. In fact, ﬂat feet can offer

the advantage of distributing the energy loss per step

over two collisions, at the heel and at the toe (Kwan

and Hubbard, 2007), (Ruina et al., 2005). More-

over, experiments on human subjects and robot proto-

types revealed that the tendon of the muscle in ankle

joint is one mechanism that favors locomotor econ-

omy (Fukunaga et al., 2001), (Wang et al., 2007). It is

predictable that by controlling and optimizing the hip

actuation and ankle compliance, the passivity-based

bipedal walker may achieve adaptive bipedal locomo-

tion with larger disturbance on uneven terrain.

Wang Q., Wang L., Zhu J., Huang Y. and Xie G. (2009).

PASSIVITY-BASED DYNAMIC BIPEDALWALKING WITH TERRAIN ADAPTABILITY - Dynamics, Control and Robotic Applications.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 29-36

DOI: 10.5220/0002184200290036

 SciTePress

In this paper, we investigate how to control

passivity-based bipedal walkers to achieve stable

walking with terrain adaptability. A powered two-

dimensional seven-link walking model with ﬂat feet

and ankle compliance has been proposed to analyze

and simulate the walking dynamics. We hypothesized

that the nervous system that controls human locomo-

tion may use optimized hip actuation and joint com-

pliance to achieve stable bipedal walking on irregular

terrain. Actually, hip actuation will cause the walker

to change locomotive patterns. Furthermore, we use

both simulations and real robot prototype to explore

the performance of the passivity-based walkers when

walk on uneven terrain by utilizing a biologically in-

spired optimization based controller, which is adap-

tive and capable of selecting proper hip actuation and

ankle compliance in view of walking stability and ef-

ﬁciency.

This paper is organized as follows. Section II de-

scribes the walking dynamics of the biped with ﬂat

feet and ankle compliance. In Section III, we present

the optimization based walking control method. In

section IV, experimental results of stable locomotion

with terrain adaptability are shown. We conclude in

Section V.

2 PASSIVITY-BASED BIPEDAL

WALKER

Our model extended the Simplest Walking Model

(Garcia et al., 1998) with the addition of hip joint

actuation, upper body, ﬂat feet and linear spring

based compliance on ankle joints, aiming for adap-

tive bipedal locomotion with optimization based con-

troller. The model consists of an upper body (point

mass added stick) that rotates around the hip joint, a

point mass representing the pelvis, two legs with knee

joints and ankle joints, and two mass added ﬂat feet

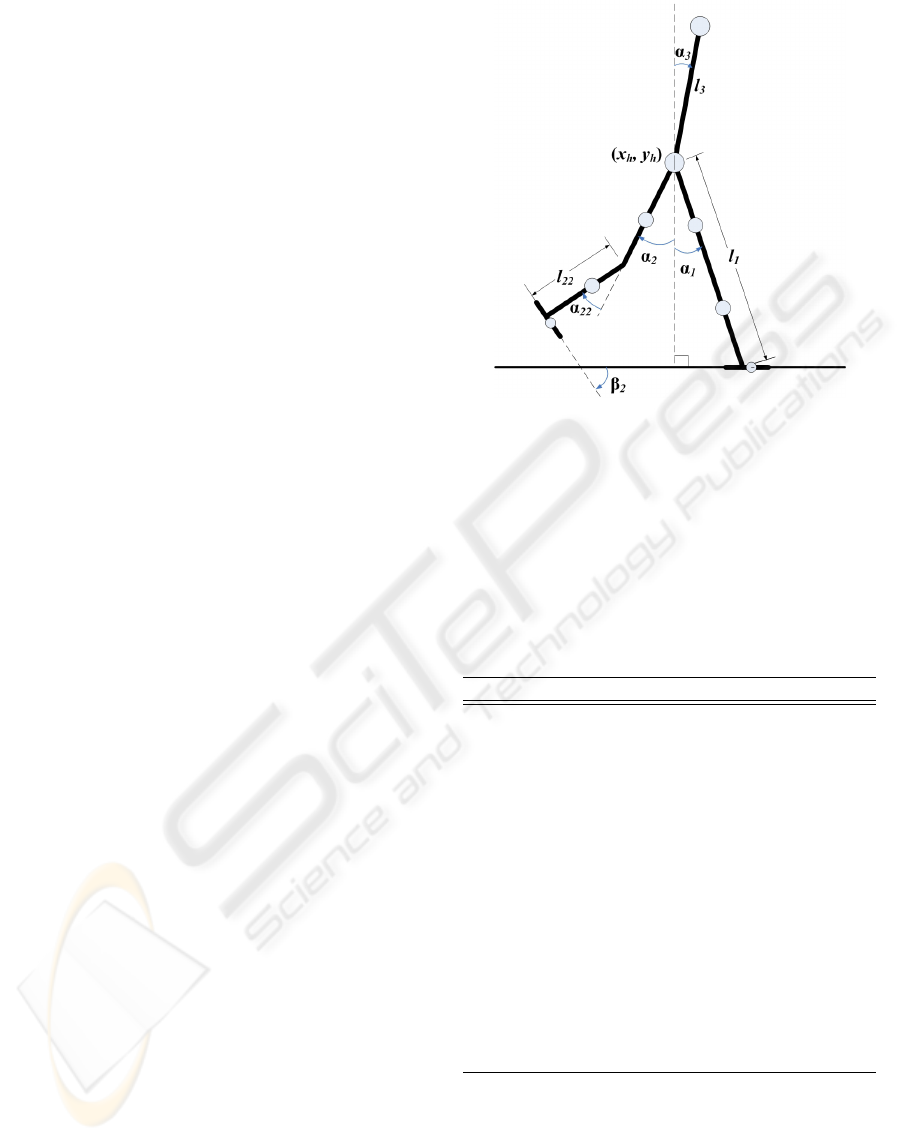
(see Fig. 1).

The mass of each leg is simpliﬁed as point masses

added on the Center of Mass (CoM) of the shank

and the thigh respectively. Similar to (Wisse et al.,

2004), a kinematic coupling has been used in the pro-

posed model to keep the body midway between the

two legs. In addition, our model added compliance

in ankle joints. Speciﬁcally, the ankle joints are mod-

eled as passive joints that are constrained by linear

springs. The model is implemented in MATLAB, us-

ing the parameter values shown in Table 1, which are

derived from the mechanical prototype.

The passive walker travels forward on level

ground. The stance leg keeps contact with the ground

while the swing leg pivots about the constraint hip.

Figure 1: Two-dimensional seven-link passive dynamic

walking model. Mechanical energy consumption of level

ground walking is compensated by applying a hip torque.

The global coordinates of the hip joint is notated as (x

, y

and α

are the angles between each leg and the vertical

axis in sagittal plane respectively. The knee joints and an-

kle joints are all passive joints. To simulate human ankle

compliance, the ankle joints of the model are constrained

by linear springs.

Table 1: Default Parameter Values for the dynamic walking

model and the following simulations.

Parameter Description Value

, m

leg mass 1.12kg

upper body mass 0.81kg

hip mass 15.03kg

, m

thigh mass 0.56kg

, m

shank mass 0.56kg

f 1

, m

f 2

foot mass 2.05kg

, l

leg length 0.7m

, l

shank length 0.35m

f 1

, l

f 2

foot length 0.15m

upper body length 0.5m

body width 0.15m

CoM of upper body 0.2m

, c

CoM of leg 0.2m

, c

CoM of shank 0.2m

k ankle stiffness 8.65Nm/rad

P hip torque 0.38Nm

To compensate the mechanical energy consumption,

similar to (Kuo, 2002), we added a hip torque P be-

tween the swing leg and the stance leg. When the ﬂat

foot strikes the ground, there are two impulses, ”heel-

strike” and ”foot-strike”, representative of the initial

impact of the heel and the following impact as the

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

whole foot contacts the ground.

The walking model can be deﬁned by the rectan-

gular coordinates x which can be described by the x-

coordinates and y-coordinates of the mass points and

the corresponding angles. The walker can also be de-

scribed by the generalized coordinates q. The springs

on the ankles constrain the foot vertical to the shank

when no heel-strike or foot-strike has occurred.

2.1 Constraint Equations

The constraint equations ξ

and ξ

used to detect heel

contact with ground are deﬁned as follows:



+ l

sinα

− l

f 1

cosα

− x

f 1

− l

cosα

− l

f 1

sinα





+ l

sinα

− l

f 2

cosα

− x

f 2

− l

cosα

− l

f 2

sinα



(1)

where x

f 1

and x

f 1

are the global x-coordinates of the

latest strike. When the ﬂat foot completely contacts

the ground, the constraint equations ξ

and ξ

used

to maintain foot contact with ground are deﬁned as

follows:



+ l

sinα

− x

f 1

− l

cosα





+ l

sinα

− x

f 2

− l

cosα



(2)

If only the heel contacts the ground, the constraint

equations ξ

and ξ

during the period before foot-

strike are deﬁned as follows:

= (x

+ l

sinα

− x

f 1

)

+ (y

− l

cosα

)

− l

f 1

= (x

+ l

sinα

− x

)

+ (y

− l

cosα

)

− l

f 2

(3)

Note that ξ

and ξ

are similar to constraining the an-

kle joint that connects shank and foot to move in a

circular orbit with heel as the center and distance be-

tween heel and ankle joint as the radius.

Similar to (Wisse et al., 2004), a reduced mass ma-

trix M

is introduced, which is deﬁned as follows:

] = [T ]

][T ] (4)

where the Jacobian T =

∂x

∂q

. Here x is the global co-

ordinates of the six pointmasses (stance shank with

foot, swing shank with foot, hip, stance thigh, swing

thigh, body), while M

is the mass matrix in global

coordinates. Matrix Ξ

transfers the independent gen-

eralized coordinates q into the constraint equation ξ

where i = 1,2,. . . , 6

dξ

(5)

Consequently, matrix

is deﬁned as follows:

∂(Ξ

˙q)

∂q

˙q (6)

2.2 Single Support Phase

Suppose that leg 1 (l

) is the stance leg, while leg 2

) is the swing leg. In the beginning of the single

support phase, the knee joint is locked (keep the shank

and the thigh in a straight line). The Equation of Mo-

tion (EoM) is described as follows:





¨q





−



(7)

where F

is the external force, while F

is the foot con-

tact force. Here, the external force F

is used to com-

pensate the mechanical energy consumption of level

ground walking, which deﬁned as follows:

} = [T ]

({F} − [M

]{ ¨x})

where F is the external force in global coordinates,

including gravity, hip actuation, and torque in com-

pliant ankle joints. Then when the swing leg is swung

forward, the knee joint releases the shank.

2.3 Heel-strike Phase

In this phase, leg 1 (l

) is still the stance leg, while leg

2 (l

) is the swing leg. The heel contacts the ground

(heel-strike occurs). The EoM of the model changes

to:





˙q





˙q

−

−eΞ

˙q

−



(8)

After the heel-strike, the foot rotates around the ankle

joint. The EoM of the model is:





0 0









¨q









−





(9)

Note that the constraint equations guarantee that the

stance leg maintains foot contact with ground and the

swing leg maintains heel contact with ground. In ad-

dition, the spring constant k in the compliant ankle

joints should not be too big. Otherwise, the stance leg

will lose contact with ground. In this phase, since the

foot rotates around the ankle joint, the force generated

by the springs on the swing leg should be considered

as external force. Thus, in this event, the mass matrix

M would not include the point mass of the swing foot.

2.4 Toe-strike Impulse

The proposed walking model with ﬂat feet introduces

a toe-strike impulse in addition to the heel-strike col-

lision. The EoM of the model is:





˙q





˙q

−

−eΞ

˙q

−



(10)

PASSIVITY-BASED DYNAMIC BIPEDALWALKING WITH TERRAIN ADAPTABILITY - Dynamics, Control and

Robotic Applications

0.2

0.4

0.6

0.8

−1.5

−1

−0.5

−2.5

−2

−1.5

−1

−0.5

0.5

(rad)

˙α

(rad /s )

˙α

(rad /s )

(a)

0 3 6 9 12 15 18 2121

0.25

0.3

0.35

0.4

0.45

0.5

0.55

0.6

time (sec)

walking velocity (m/s)

k=1.65 Nm/rad

k=8.65 Nm/rad

k=15 Nm/rad

k=25 Nm/rad

k=35 Nm/rad

stiff ankle

(b)

Figure 2: (a) Basin of attraction of the passive dynamic

walking model with ﬂat feet and compliant ankles. The

blue layers of points represent horizontal slices of a three-

dimensional region of initial conditions that eventually re-

sult in the cyclic walking motion. The ﬁxed point is indi-

cated with a red point, which is above one of the sample

slices. (b) Results of actively changing walking speed with

the same hip actuation and different ankle compliance (k

varies).

Note that in this phase, we consider that the ankle

joint of the swing leg is constrained to move in a cir-

cular orbit with toe as the center and distance between

toe and ankle joint as the radius. The force generated

by the spring on the swing leg should be considered

as external force, which can also be considered as the

constraint force of the circular orbit. After the toe-

strike, one step ends.

2.5 Effects of Hip Actuation and Ankle

Compliance

By application of the cell mapping method that has

been used in the several studies of passive dynamic

walking (e.g. (Wisse et al., 2004), (Wisse et al.,

2007)), we found that the model performs well in

the concept of global stability. The allowable er-

rors can be much larger than the results obtained in

(Wisse et al., 2004). This can be inspected by the

evaluation of the basin of attraction as shown in Fig.

2(a), which is the complete set of initial conditions

that eventually result in cyclic walking motion. One

can ﬁnd that cyclic walking with initial conditions

in Table 1, emerges even if the initial step is nearly

fourfold as large, e.g. {α

(0) = 0.8,

(0) = −2.3,

(0) = −0.8}. It indicates that passive dynamic

walking with ﬂat feet and ankle compliance may play

better on rough terrain with ground disturbance.

It has been examined that optimized hip actuation

can improve the stability of the passive walker (Kurz

and Stergiou, 2005). In addition, one can use the hip

actuation as the control parameter to achieve stable

walking on uneven terrain (Schuitema et al., 2005)-

(Ueno et al., 2006). In our model mentioned above,

ankle compliance k can also be used as a control pa-

rameter to affect the walking gait. As shown in Fig.

2(b), under the same change of hip actuation, different

ankle compliance reveals different responses in walk-

ing velocity transition. It indicates that more compli-

ance results in more visible sensitivity to the change

of hip torque. According to the analysis of basins of

attraction with different k (Wang et al., 2007), we ﬁnd

that a relatively small k will lead to more stable points.

However, more compliance in ankle joints may result

in often falling backward during walking. Thus, op-

timized ankle compliance may result in a more stable

bipedal walking that allows larger disturbance.

3 OPTIMIZATION BASED

WALKING CONTROL

In order to optimize the hip actuation and ankle com-

pliance which affect walking gait as analyzed above,

Particle Swarm Optimization (PSO) has been chosen

with a focus lying on quickly ﬁnding suitable results,

in view of time-consuming and adaptivity of the gait.

In the realization of the PSO algorithm, a swarm of

N particles is constructed inside a D-dimensional real

valued solution space, where each position can be a

potential solution for the optimization problem. The

position of each particle is denoted as X

(0 < i < N).

Each particle has a velocity parameter V

(0 < i < N).

It speciﬁes that the length and the direction of X

should be modiﬁed during iteration. A ﬁtness value

attached to each location represents how well the lo-

cation suits the optimization problem. The ﬁtness

value can be calculated by a ﬁtness function of the

optimization.

In this study, we used adaptive PSO with changing

inertia weight. The update equation for velocity with

inertial weight is described as follows:

k+1

= wv

+ c

(pbest

− x

) + c

(gbest

− x

)

(11)

where w is the inertia weight. v

is one component

of V

(d donates the component number) at iteration

k. Similarly, x

is one component of X

at iteration

k. pbest

(0 < i < N) and gbest are the personal best

position and the global best position at each iteration

respectively. c

and c

are acceleration factors. r

and

are random numbers uniformly distributed between

0 and 1. Note that each component of the velocity has

new random numbers. In order to prevent particles

from ﬂying outside the searching space, the ampli-

tude of the velocity is constrained inside a spectrum

[−v

max

, +v

max

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

3.1 Fitness Function and Optimization

Process

For a speciﬁc passive walker, the mechanical param-

eters (length and mass distribution) are constant. To

control passive dynamic walking on uneven terrain,

we focus the control parameters on hip actuation P

and ankle compliance k. Then the two-dimensional

parameter space is (P, k). Here a set of parameters

stands for a particle of PSO. Since the walker will be

optimized with integration of stability and efﬁciency,

the ﬁtness function is deﬁned as follows:

σ = σ

+ γσ

(12)

where σ

and σ

are the ﬁtness value to assess the sta-

bility and efﬁciency of each set of parameters respec-

tively. γ is the tuning factor to change the importance

of the two characteristics.

There are several methods to evaluate the stabil-

ity of the passive dynamic walking. In this study,

the stability will be quantiﬁed by the modulus of the

Jacobian matrix of the mapping function as deﬁned

in (Wisse et al., 2004). Here, we notate the maxi-

mal eigenvalue as λ

, which represents the decreas-

ing speed of the deviation. The stability grades varies

for different sets of parameters even they all have a

stable ﬁxed point. The smaller the λ

is, the faster the

deviation decreases and the more stable the walker is.

The similar conclusion can be obtained when all sets

of parameters only have an unstable ﬁxed point. The

larger the λ

is, the more far from the stable state the

walker is. Then we deﬁne the ﬁtness function of sta-

bility as the follows:

(13)

Similar to (Collins et al. 2005) and (Wisse et al.,

2004), the energetic efﬁciency of walking can be eval-

uated by the speciﬁc resistance as follows:

Θ =

MgL

(14)

where E is the cost of energy. In this study, the energy

cost is generated only by the hip torque. M is the total

mass of the model. g is the acceleration of gravity. L

is the length of distance the robot passed. Then the

ﬁtness function can be deﬁned as follows:

Mgl

(15)

From (12), (13) and (15), we can obtain the whole

expression of the ﬁtness function:

σ =

+ γ

Mgl

(16)

Figure 3: The control scheme to overcome ground distur-

bance with optimized hip torque and ankle compliance.

Additionally, to evaluate the walking motion after

overcoming ground disturbance, we introduce an-

other expression of ﬁtness function. We use further

walking distance d instead of the ﬁtness efﬁciency σ

Then the ﬁtness function can be rewritten as:

σ =

+ γd (17)

3.2 Gait Controller with Optimized

Parameters

After analyzing the effects of hip actuation and an-

kle compliance in the stability and adaptability of the

passive dynamic walker, we select P and k as the gait

control input. The output of the optimization simula-

tor P

(t) and k

(t) are added to the current actual hip

actuation P

(t) and ankle compliance k

(t) (see Fig.

3).

This results in extra hip torque to move the swing

leg more forward and prevent tripping. The purpose

of the failure-detection block in Fig. 3 is to monitor

in simulations the foot contact and the knee locking

in order to detect whether walking failed. A failure

means that the robot fell either backward or forward

or that it started running (both feet leave contact with

ground). There is a active control counter module in

the diagram. It is used to count the times of applying

active control (increasing or decreasing P or k) during

one continuous walking. The output of this module

make the simulator change P or k. With the dynamic

model that adequately describing the real robot, an

adaptive optimizing control scheme can be done with-

out manually set to teach the robot and without the

robot damaging itself.

4 EXPERIMENTAL RESULTS

All the simulation experiments used the dynamic

model mentioned in Section II which was imple-

PASSIVITY-BASED DYNAMIC BIPEDALWALKING WITH TERRAIN ADAPTABILITY - Dynamics, Control and

Robotic Applications

1 2 3 4 5 6

generation

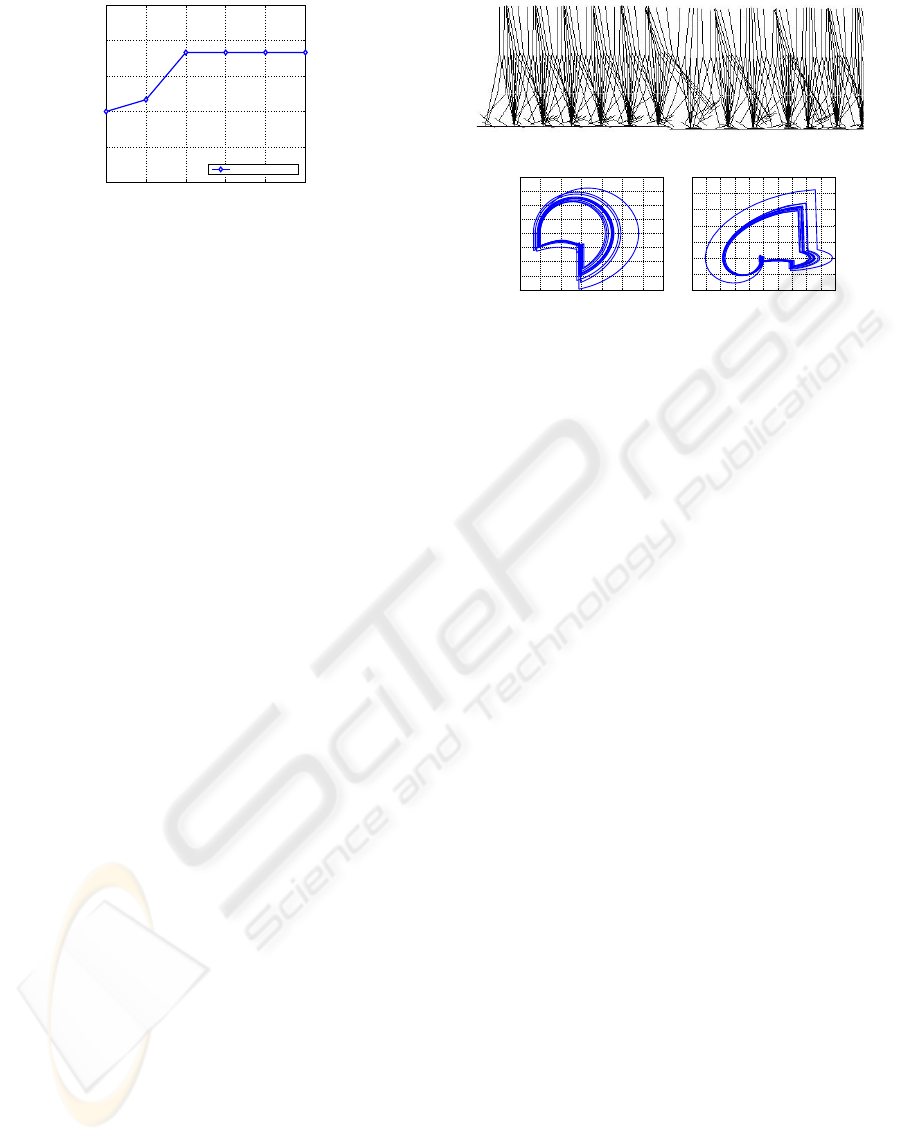
ground disturbance (mm)

adaptable disturbance

Figure 4: Maximum ground disturbance with optimized hip

torque and ankle compliance that keep unchanged during

stable walking.

mented in MATLAB, using the parameter values

shown in Table 1. The numerical integration of the

second order differential EoMs uses the Runge-Kutta

method, which is similar to the simulation methods

mentioned in (Wisse et al., 2004).

4.1 Parameter Optimization

Based on the adaptive PSO with proper inertial weight

mentioned above, we optimized the hip torque (hip

actuation) and ankle compliance to achieve adaptive

walking with maximal allowable ground disturbance

of the model with parameter values in Table 1. The

testing scenario is a ﬂoor with one step down. The

height of the step is gradually chosen from the range

from 1mm to 20mm. The initial particles which rep-

resent the parameter set of P and k are randomly se-

lected from the corresponding points in 2(a) that will

ﬁnally achieve stable walking. During the walking

simulation of the dynamic model, the ground distur-

bance gradually increase. The optimization process

evaluates the maximum ground disturbance of the dy-

namic model with certain P and k. During the walk-

ing, the selected P and k keep constant to overcome

gradually increased ground disturbance. The opti-

mization ﬁnally record the maximum ground distur-

bance in each generation. The ﬁtness function is (16).

Fig. 12 shows the results. It is clear that by apply-

ing the adaptive PSO, the optimization process can

quickly ﬁnd the optimal parameter set. It also in-

dicated that with optimized hip actuation and ankle

torque, the passive dynamic walker can achieve stable

walking with no active control even if there is −11mm

ground disturbance.

4.2 Walking on Uneven Terrain with

Control

Starting from the optimized P and k with no active

control during walking simulations, we add the con-

trol scheme shown in Fig. 3 to the walking motion.

(a)

−0.4 −0.2 0 0.2 0.4 0.6 0.8 1

−4

−3

−2

−1

angle of thigh (rad)

angular velocity of thigh (rad/s)

(b)

−1.2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6

−10

−5

angular velocity of shank (rad/s)

angle of shank (rad)

(c)

Figure 5: Adaptive locomotion with active control on un-

even terrain. This result is obtained every 10 frames during

a continuous walking. (a) is the stick diagram. (b) and (c)

are the angular trajectories of the thigh and shank respec-

tively.

A preset ground disturbance occurs at known time

during the level walking. The active control counter

determines the times of active control to change P

and k. In this simulation, the ground disturbance

varies from −15mm to −25mm. The ﬁtness function

of the optimization is (17). The counter ﬁrst makes

the optimization simulator to actively change P and

k once when ground disturbance occurs. There was

no optimized set of P and k that can overcome the

−25mm step. Then the counter makes the simulator

to actively change P and k twice when ground distur-

bance occurs. The walker successfully achieved sta-

ble walking with −25mm disturbance (see stick dia-

gram shown in Fig. 5(a)). Fig. 5(b) and (c) show the

trajectories of hip and knee during the adaptive walk-

ing.

Note that the cyclic walking was initially actuated

by a relatively small hip torque. After one time of ac-

tive control (varying P and k), the hip torque increased

to move the swing leg more forward and prevent trip-

ping. Since there was a second time of active con-

trol, the trajectories of the swing thigh and the swing

shank transited to bigger limit cycles. Such optimized

P and k ﬁnally stabilized the walking motion after a

step down occurred.

Fig. 6 shows the optimization process of the

hip actuation and ankle compliance during the walk-

ing with two times of active control. We set that if

the walker can walk stably for enough time after the

ground disturbance, the walking motion is adaptive

on the uneven ground. Speciﬁcally, the distance is

the product of walking speed times 25 seconds. Fig.

6(a) demonstrates the results of further distance after

ground disturbance each generation. After four gen-

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

1 2 3 4 5 6 7 8 9

generation

further distance (m)

(a)

17.6

17.8

18.2

18.4

18.6

14.5

15.5

hip torque (Nm)ankle compliance (Nm/rad)

further distance (m)

(b)

Figure 6: Optimization of hip actuation and ankle compli-

ance. Both P and k vary during the continuous walking.

(a) is the results of further distance after ground disturbance

each generation. (b) is the results of selecting hip actuation

and ankle compliance during optimization.

erations, the walker can ﬁnd optimized parameters to

overcome the step. Fig. 6(b) shows the process of

selecting P and k during the optimization. The ini-

tial hip torque is 5.5130Nm and ankle compliance is

12.2218Nm/rad. The two times of variance of P and

k are (18.0000Nm, 16.0000Nm/rad and (5.5000Nm,

15.4228Nm/rad) respectively.

Though there is no complex learning algorithm

in the control scheme, the walker can perform better

terrain adaptability comparing with other simulation

results (e.g. (Schuitema et al., 2005), (Wang et al.,

2006)).

4.3 Real Robot Experiments

To study natural and energy-efﬁcient bipedal walking,

we designed and constructed a bipedal robot proto-

type, 1.2m in height and 20kg in weight. With the bi-

secting hip mechanism similar to (Wisse et al., 2007),

the prototype has ﬁve Degrees of Freedom (DOFs).

Two commercial motors are used in the hip joints to

perform hip actuation. Each leg consists of a thigh

and a shank interconnected through a passive knee

joint that has a locking mechanism. Springs are in-

stalled between the foot and the plate that is pushing

the leg up while it is rotated around the ankle. To pre-

vent foot-scufﬁng, we modiﬁed the foot with arc in

the front and the back-end. Speciﬁc mechanical pa-

rameters are shown in Table 1. In the experiment, by

using the proposed method, the robot tried to walk on

natural ground outdoor. The natural ground is not a

strict continuous level ﬂoor, where random irregular-

ity of the ground and slight slippery occurred. Fig. 7

shows the result.

The robot can achieve three-dimensional sta-

ble walking on natural ground with more than 10

steps. Comparing to the results of terrain adapt-

ability of other real robot experiments (e.g. two-

dimensional walkers (Wisse et al., 2005), (Ueno et al.,

2006)), the successful three-dimensional walking of

the robot prototype shows that the quasi-passive dy-

Figure 7: A sequence of photos captured during au-

tonomous walking of the robot prototype on natural ground.

namic walker with optimized hip actuation and ankle

compliance can perform stable walking with larger

ground disturbance.

5 CONCLUSIONS

In this paper, we have investigated how to control

passivity-based bipedal walkers to achieve stable lo-

comotion with terrain adaptability. Satisfactory re-

sults of simulations and real robot experiments in-

dicated that having the ﬁxed mechanical parameters

during walking, the passivity-based walker can walk

on uneven terrain with larger ground disturbance by

optimized hip actuation and ankle compliance in view

of walking stability and efﬁciency. In the future, more

real robot experiments will be continued to overcome

more complex ground disturbance.

ACKNOWLEDGEMENTS

The authors would like to thank M. Wisse for shar-

ing the simulation ﬁles of the simplest walking model.

This work was supported by the National Natural Sci-

ence Foundation of China (No. 60774089), National

High Technology Research and Development Pro-

gram of China (863 Program) (No. 2006AA04Z258)

and 985 Project of Peking University.

REFERENCES

S. Collins, M. Wisse, A. Ruina, A three-dimensional

passive-dynamic walking robot with two legs and

knees, International Journal of Robotics Research,

vol. 20, pp. 607-615, 2001.

S. Collins, A. Ruina, R. Tedrake, M. Wisse, Efﬁcient

bipedal robots based on passive-dynamic walkers, Sci-

ence, vol. 307, pp. 1082-1085, 2005.

PASSIVITY-BASED DYNAMIC BIPEDALWALKING WITH TERRAIN ADAPTABILITY - Dynamics, Control and

Robotic Applications

R. Eberhart, J. Kennedy, Particle swarm optimization, Proc.

of the IEEE Conf. on Neural Network, 1995, pp. 1942-

1948.

T. Fukunaga, K. Kubo, Y. Kawakami, S. Fukashiro, H.

Kanehisa, C. N. Maganaris, In vivo behaviour of hu-

man muscle tendon during walking, Proc. Biol. Sci.,

vol. 268, pp. 229-233, 2001.

M. Garcia, A. Chatterjee, A. Ruina, M. Coleman, The sim-

plest walking model: stability, complexity, and scal-

ing, ASME Journal Biomechanical Engineering, vol.

120: pp. 281–288, 1998.

Y. Guan, E. S. Neo, K. Yokoi, and K. Tanie, Stepping over

obstacles with humanoid robots, IEEE Transactions

on Robotics, 22(5), pp. 958-973, 2006.

Honda Motor Co., Ltd. New asimo - running at

6km/h, http://world.honda.com/HDTV/ASIMO/New-

ASIMO-run-6kmh/, 2005.

M. Kwan, M. Hubbard, Optimal foot shape for a passive

dynamic biped, Journal of Theoretical Biology, vol.

248, pp. 331-339, 2007.

A. D. Kuo, Energetics of actively powered locomotion

using the simplest walking model, ASME Journal

Biomechanical Engineering, vol. 124, pp. 113-120,

2002.

M. J. Kurz, N. Stergiou, An artiﬁcial neural network that

utilizes hip joint actuations to control bifurcations and

chaos in a passive dynamic bipedal walking model,

Biol. Cybern., vol. 93, pp. 213-221, 2005.

T. McGeer, Passive dynamic walking, International Journal

of Robotics Research, vol. 9, pp. 68-82, 1990.

P. Michel, J. Chestnutt, S. Kagami, K. Nishiwaki, J.

Kuffner, and T. Kanade, GPU-accelerated real-time

3D tracking for humanoid locomotion and stair climb-

ing, Proc. of the IEEE/RSJ Int. Conf. on Intelligent

Robots and Systems, 2007, pp. 463–469.

A. Ruina, J. E. A. Bertram, M. Srinivasan, A collisional

model of the energetic cost of support work quali-

tatively explains leg sequencing in walking and gal-

loping, pseudo-elastic leg behavior in running and the

walk-to-run transition, Journal of Theoretical Biology,

vol. 237, no. 2, pp. 170-192, 2005.

E. Schuitema, D. Hobbelen, P. Jonker, M. Wisse, J. Karssen,

Using a controller based on reinforcement learning for

a passive dynamic walking robot, Proc. of the IEEE-

RAS Int. Conf. on Humanoid Robots, 2005, pp. 232-

237.

R. Smith, U. Rattanaprasert, and N. O’Dwyer, Coordination

of the ankle joint complex during walking, Huamn

Movement Science, vol. 20, pp. 447-460, 2001.

R. Tedrake, T. W. Zhang, M. F. Fong, H. S. Seung, Actu-

ating a Simple 3D Passive Dynamic Walker. In Proc.

IEEE Int. Conf. Robotics and Automation, 2004, pp.

4656-4661.

T. Ueno, Y. Nakamura, T. Takuma, K. Hosoda, T. Shibata

and S. Ishii, Fast and stable learning of quasi-passive

dynamic walking by an unstable biped robot based on

off-policy natural actor-critic, Proc. of the IEEE/RSJ

International Conference on Intelligent Robots and

Systems, 2006, pp. 5226-5231.

S. Wang, J. Braaksma, R. Babu ˇska, D. Hobbelen, Re-

inforcement learning control for biped robot walk-

ing on uneven surfaces, Proc. of the 2006 Interna-

tional Joint Conference on Neural Networks, 2006,

pp. 4173-4178.

Q. Wang, J. Zhu, L. Wang, Passivity-based three-

dimensional bipedal robot with compliant legs, Proc.

of the SICE Annual Conference, 2008.

M. Wisse, A. L. Schwab, F. C. T. Van der Helm, Passive

dynamic walking model with upper body, Robotica,

vol. 22, pp. 681-688, 2004.

M. Wisse, A. L. Schwab, R. Q. van der Linde, F. C. T.

van der Helm, How to keep from falling forward: el-

ementary swing leg action for passive dynamic walk-

ers, IEEE Transactions on Robotics, vol. 21, no. 3, pp.

393-401, 2005.

M. Wisse, G. Feliksdal, J. van Frankenhuyzen, B. Moyer,

Passive-based walking robot - Denise, a simple, efﬁ-

cient, and lightweight biped, IEEE Robotics and Au-

tomation Magazine, vol. 14, no. 2, pp. 52-62, 2007.

J. Yamaguchi and A. Takanishi, Development of a leg part

of a humanoid robot - development of a biped walk-

ing robot adapting to the humans’ normal living ﬂoor,

Autonomous Robots 4(4), pp. 369-385, 1997.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics