BUSINESS ANALYSIS IN THE OLAP CONTEXT

Emiel Caron

Erasmus University Rotterdam, ERIM Institute of Advanced Management Studies

P.O. Box 1738, 3000 DR, Rotterdam, The Netherlands

Hennie Daniels

a,b

Center for Economic Research, Tilburg University

P.O. Box 90153, 5000 LE, Tilburg, The Netherlands

Keywords: Business Intelligence, Multi-dimensional databases, OLAP, Sensitivity analysis, Explanation, Data mining.

Abstract: Today's multi-dimensional business or OnLine Analytical Processing (OLAP) databases have little support

for sensitivity analysis. Sensitivity analysis is the analysis of how the variation in the output of a

mathematical model can be apportioned, qualitatively or quantitatively, to different sources of variation in

the input of the model. This functionality would give the OLAP analyst the possibility to play with ``What

if...?''-questions in an OLAP cube. For example, with questions of the form: ``What happens to an

aggregated value in the dimension hierarchy if I change the value of this data cell by so much?'' These types

of questions are, for example, important for managers that want to analyse the effect of changes in sales,

cost, etc., on a product's profitability in an OLAP sales cube. In this paper, we describe an extension to the

OnLine Analytical Processing (OLAP) framework for business analysis in the form of sensitivity analysis.

1 INTRODUCTION

In this paper, a new OLAP database operator is

described that supports the analyst in answering

these managerial sensitivity analysis questions in an

OLAP data cube. For example, an analyst while

navigating an OLAP cube, might be interested in the

question: How is the profit in the year 2008 for a

certain product affected when its unit price is

changed ceteris paribus (c.p.) with one extra unit or

one percent in the sales model? Such question might

be `dangerous', when the change is not caused by a

variable in the base cube, but by a variable on some

intermediate aggregation level in the cube. The latter

situation makes the OLAP database mathematically

inconsistent.

Consistency in a set of OLAP equations is not

trivial because by changing a certain variable (c.p.),

a system of equations can become inconsistent. For

instance, missing data, dependency relations, and the

presence of non-linear relations in the business

model can cause an OLAP system to become

inconsistent. It is therefore important to investigate

the criteria for consistency and solvability in the

OLAP context. Our novel OLAP operator corrects

for such inconsistencies such that the analysts can

still carry out sensitivity analysis in the OLAP

context. Moreover, we elaborate on two important

mathematical conditions for sensitivity analysis in

the OLAP context namely consistency and

solvability of the system of OLAP equations. For

this purpose, we distinguish between linear systems

of OLAP equations, associated with dimension

hierarchies, and nonlinear systems of OLAP

equations, generally associated with business

models.

Sensitivity analysis in the OLAP context is

related to the notion of comparative statics in

economics or sensitivity analysis in engineering.

Where the central issue is to determine how changes

in independent variables affect dependent variables

in an economic model (Samuelson, 1941).

Comparative statics is defined as the comparison of

two different equilibrium states solutions, before and

after change in one of the independent variables,

keeping the other variables at their original values.

The basis for comparative statics is an economic

model that defines the vector of dependent variables

, y

, …, y

as functions of the vector of

325

Caron E. and Daniels H. (2009).

BUSINESS ANALYSIS IN THE OLAP CONTEXT.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

325-330

DOI: 10.5220/0001989103250330

 SciTePress

independent variables x

, x

, …, x

. In this paper we

apply comparative statics in the OLAP context

where we have a system of linear or nonlinear

equations with dependent variables on an aggregated

level of the cube, called non-base variables and

independent variables on the base level, called base

variables.

This research is part of our continued work on

extensions for the OLAP framework for business

diagnosis. Current OLAP databases have limited

capabilities for sensitivity and diagnostic analysis.

The goal of our research is to largely automate these

manual diagnostic discovery processes (Caron and

Daniels, 2007). In (Sarawagi et al., 1998) a similar

research approach is taken.

The remainder of this paper is organized as

follows. Section 2 introduces our notation for multi-

dimensional equations, followed by formal

description of consistency and solvability of systems

of OLAP equations in Section 3. In addition, we

show that systems of OLAP equations are consistent

and have a unique solution. In Section 4 the OLAP

framework is extended with sensitivity analysis

based on the consistency property. Subsequently, we

briefly describe a software implementation of our

model for OLAP sensitivity analysis. Finally,

conclusions are discussed in Section 6.

2 NOTATION AND EQUATIONS

The multi-dimensional OLAP database is a

framework used to provide business decision-makers

with the ability to perform dynamic data analysis.

With OLAP tools, users gain access to the data

warehouse. Decision-makers tend to have questions

that are often multi-dimensional in nature and

demand fast access to large amounts of aggregated

data. A typical business question might be: ``What

was the profit of product A this year, in region X,

per sales office, compared with the previous version

of the product, compared to the targeted profit?'' For

decision-making purposes it might be necessary that

the answer to this question is explored further, for

example on the quarter, month and week level. This

functionality is provided by OLAP.

Two important data schemata for the design of a

multi-dimensional database are the star schema and

the snowflake schema. OLAP typically uses a star

schema, where data is stored in fact tables and

dimension tables. In a star schema, one central fact

table is linked via foreign keys with several

dimension tables. Each dimension has its own single

table with a smaller set of data. The other important

multi-dimensional design approach, the snowflake

schema, is a non-redundant database design that

characterises itself by the normalized data approach

where data is further split into additional dimension

tables (Han and Kamber, 2005).

In both schemata data is organized using the

dimensional modelling approach, which classifies

data into measures (i.e., facts) and dimensions.

Measures are numeric and dimensions are

categorical data types. Measures like are the basic

units of interest for analysis. Dimensions correspond

to different perspectives for viewing measures.

Dimensions are usually organized as dimension

hierarchies, which offer the possibility to view

measures at different dimension levels (e.g. month

p quarter p year is a hierarchy for the Time

dimension). Aggregating measures up to a certain

dimension level, with functions like sum, count, and

average, creates a multidimensional view of the data,

also known as the data cube. A number of data cube

operations exist to explore the multidimensional data

cube.

Here we use a generic notation for multi-

dimensional data schemata that is particularly

suitable for combining the concepts of measures,

dimensions, and dimension hierarchies as described

in (Caron and Daniels, 2007). Therefore, we define a

measure y as a function on multiple domains:

ii i i

yDD D××× →

K R

(1)

Each domain

D has a number of hierarchies ordered

max

kk k

DD DppKp

, where

D is the lowest

level and

max

D is the highest level in

max

D . A

dimension’s top level has a single level instance

{

}

max

All

D = . For example, for the time dimension

we could have the following hierarchy

TTp

Tp , where

{

}

T All-T= ,

{}

T 2000,2001= , and

{

}

Q1,Q2,Q3,Q4T = . A cell in the cube is denoted

(, , , )

dd dK , where the 's

d are elements of

the domain hierarchy at some level, so for example

(2000, Amsterdam, Beer) might be a cell in a sales

cube. Each cell contains data, which are the values

of the measures y like, for example,

211

sales (2000,

Amsterdam, Beer). The measure’s upper indices

indicate the level on the associated dimension

hierarchies. If no confusion can arise we will leave

out the upper indices indicating level hierarchies and

write sales (2000, Amsterdam, Beer). Furthermore,

the combination of a cell and a measure is called a

data point. The measure values at the lowest level

cells are entries of the base cube. If a measure value

ICEIS 2009 - International Conference on Enterprise Information Systems

326

is on the base cube level, then the hierarchies of the

domains can be used to aggregate the measure

values using aggregation operators like SUM,

COUNT, or, AVG.

By applying suitable equations, we can alter the

level of detail and map low level cubes to high level

cubes and vice versa. For example, aggregating

measure values along the dimension hierarchy (i.e.

rollup) creates a multidimensional view on the data,

and de-aggregating the measures on the data cube to

a lower dimension level, creates a more specific

cube.

Here we investigate the common situation where

the aggregation operator is the summarization of

measures in the dimension hierarchy. So y is an

additive measure or OLAP equation (Lenz and

Shoshani, 1997) if in each dimension and hierarchy

level of the data cube:

11 1

(,,) (,,)

qn qn

ii i ii i

yaya

∑

KK KK

KK K K

(2)

where

∈ ,

aD∈ , q is some level in the

dimension hierarchy, and J represents the number of

level instances in

D . An example equation

corresponding to two roll-up operations reads:

212

420

102

sales (2001, All-Locations, Beer)

sales (2001.Q ,Country ,Beer).

∑∑

3 SOLVABILITY

In comparative statics in economics the central issue

is to determine how changes in independent

variables affect dependent variables in an economic

model. Comparative statics is based on an economic

model (i.e., a system of equations) that defines the

vector of dependent variables y as functions of the

vector of independent variables x. In the OLAP

context we have a system of linear equations with

dependent variables on an aggregated level of the

cube, called non-base variables and independent

variables on the base level, called base variables. A

condition for the application of comparative statics

is that the underlying system of equations is

mathematical consistent.

The data structure in an OLAP cube represents a

system of additive equations in the form of a

aggregation lattice (Han and Kamber, 2005). The

top of the lattice is the apex cube

max max max

ii i

and the

bottom of the the lattice is represented by the base

variables

00 0

. The upset of a base variable in the

lattice represents non-base variables on specific

levels of aggregation in the OLAP cube. For

example, the non-base variable

(1)

ii i i

+KK

is a

parent of the non-base variable

12 pn

ii i i

somewhere in the lattice. Roll-ups can be alternated

from one dimension to the next by the data analyst,

resulting in multiple paths from a base variable to a

non-base variable in the aggregation lattice.

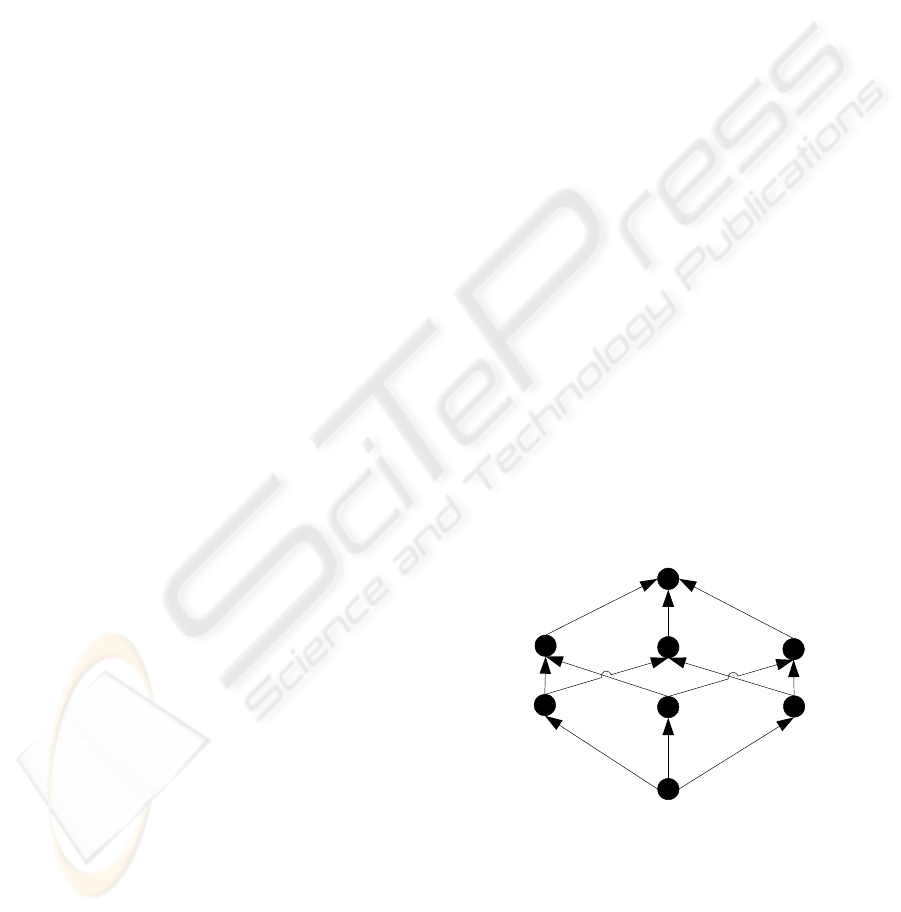
An example aggregation lattice is given for the

variable sales (

123

ii i

) from an example sales

datacube in figure 1, where the indices represent the

customer, product, and store dimension,

respectively. In the lattice the variable

101

y , which

has a number of data instances, has instances of the

root in its upset and instances of the variables

{

100

y ,

001

y ,

000

} in its downset. All non-base

variables

y are aggregated from instances of the base

variables

000

(customer, product,store)x . The length

of a path from a non-base variable

12 n

ii i

in the

lattice to a base variable

00 0

12 n

ii i++ +K .

Obviously, the sum of the indices of a non-base

variable corresponds with the number of

aggregations carried out. Non-base variable in the

system of OLAP equations are the result of

aggregation operators in the lattice structure.

Moreover, a non-base variable in the lattice

corresponds with a single equation expressed in a

unique set of base variables. This property can be

easily verified by substituting all equations in the

downset of a non-base variable from its current level

to the base level.

A system of OLAP equations as in equation (2),

where the functions are linear, can be written in

matrix form as:

z = c

(3)

where A is an m×n coefficient matrix of constants,

is an m×1 vector of constants, and

z is an n×1 vector

of variables for which we need solutions. In the next

section below, we discuss relevant matrix theory on

the conditions under which equation (3) is consistent

and solvable. Moreover, we transfer the matrix

theory to a system of implicit equations with

independent and dependent variables that

corresponds to a system of additive OLAP

equations. This system of equations lets us study the

impact of a change in one or more base variables

(c.p.) on a non-base variable. The matrix form of

this system of equations is A

z = 0; the matrix A is

partitioned as [A

], where A

is the coefficient sub

BUSINESS ANALYSIS IN THE OLAP CONTEXT

327

matrix for non-base variables and A

is the

coefficient sub matrix for base variables. And the

vector of variables

z is partitioned in non-base

variables

y and base variables x as z' = [y x].

The equations of the OLAP aggregation lattice

in (3) are rewritten in the following partioned matrix

form:

AAyx0+=

(4)

where A

is a m × n matrix of constants, A

is a m × l

matrix of constants,

y ∈ R

is vector of all non-base

variables, from all levels in the aggregation lattice,

for which solutions are needed, and

00 0 l

∈

R is a

vector of base variables that are given. The above

system of equations in (4) is the collection of all

possible drilldown equations in the OLAP database

by drilling down from the root of the lattice to the

base over all possible dimensions and dimension

hierarchies. This system of equations is clearly

overspecified, because a non-base variable in the

lattice might be the right hand side in multiple

drilldown equations. In fact, each possible drilldown

from one dimension to the next, results in an

additional equation for a non-base variable. From

the substation argument above it follows that

equation (4) has a unique solution y for a given set

of base variables x.

This implies

12 1

(| ) ()rank A A rank Ax−= , see

theorem 6.1 from (Schott, 1997), for all x so the

columns of A

are linear combinations of the

columns of A

, so

AZ= where a Z is a n × l

matrix of constants.

Furthermore, since the solution for y is unique

we have

()rank A n= because the null space of A

(){}NA 0= . So also Z is unique since

ZAZ= would imply

(*)0AZ Z−= and

because

(){}NA 0= , we have *

Z= . It is also

easy to show that

−

(5)

where

−

is the left generalized inverse (e.g. the

Moore-Penrose inverse) of

. This exists because

()rank A n= and satisfies

11 n

−

= , see theorem

6.6 from (Schott, 1997).

To show (5) note that

ZA= implies:

11211121 2

A A AA AA AZ A

−−

===

(6)

−

is another solution of

ZA= and there-

fore

−

= by uniqueness. Because of (6) it can

be shown that the OLAP aggregation lattice always

has a unique solution for the non-base variables for a

given a set of base variables.

4 SENSITIVITY ANALYSIS

Because a system of OLAP equations is uniquely

solvable, a change in a single base variable (c.p.) in

the aggregation lattice will result in a new unique

solution for the non-base variables. If a non-variable

(,,)

ii i

KK is changed with some magnitude

(c.p.) the aggregation lattice will obviously become

inconsistent because its down set variables are not

changed accordingly. This is demonstrated with the

following 2 example equations that are derived from

the aggregation lattice in Figure 1 where an instance

of the variable

101

is changed with some Δ:

111 101

101 100

1. ( , , )

2. (,,) (,,)

yya

ya ya

+Δ= +Δ

+Δ≠

∑

KK K K

In the first equation we see that variables in the

upset of

101

y incorporate the change resulting in a

consistent equation. However, in the second

equation we see that the system becomes

inconsistent, because in the down set of

101

y , i.e. the

variables on the right hand side of the equations,

remain on their initial values. In that case, sensitivity

analysis is ‘dangerous’ because it results in an

inconsistent system of OLAP equations.

101

000

010

100

011

110

111

001

product

Figure 1: Aggregation lattice for the sales cube.

Now we have to correct the down set of the variable

(,,)

ii i

KK for the change from each

associated lower level aggregation level to the base

cube level. This correction makes the sensitivity

procedure again useful for the complete aggregation

ICEIS 2009 - International Conference on Enterprise Information Systems

328

lattice. In the correction procedure all variables in

the down sets of siblings of

1 qn

ii i

(,,)

aKK have

to remain on their norm values and one variable on

each level of the down set of

(,,)

ii i

KK has

to be corrected with the specified change. The

variables on the base cube level are corrected in the

final step.

5 SOFTWARE IMPLEMENTAION

In this section, we shortly present the most important

concepts of the prototype software implementation

of the sensitivity analysis model in MS Excel/

Access in combination with Visual Basic. This

application is initially programmed to perform

experiments and analyses necessary for a case study.

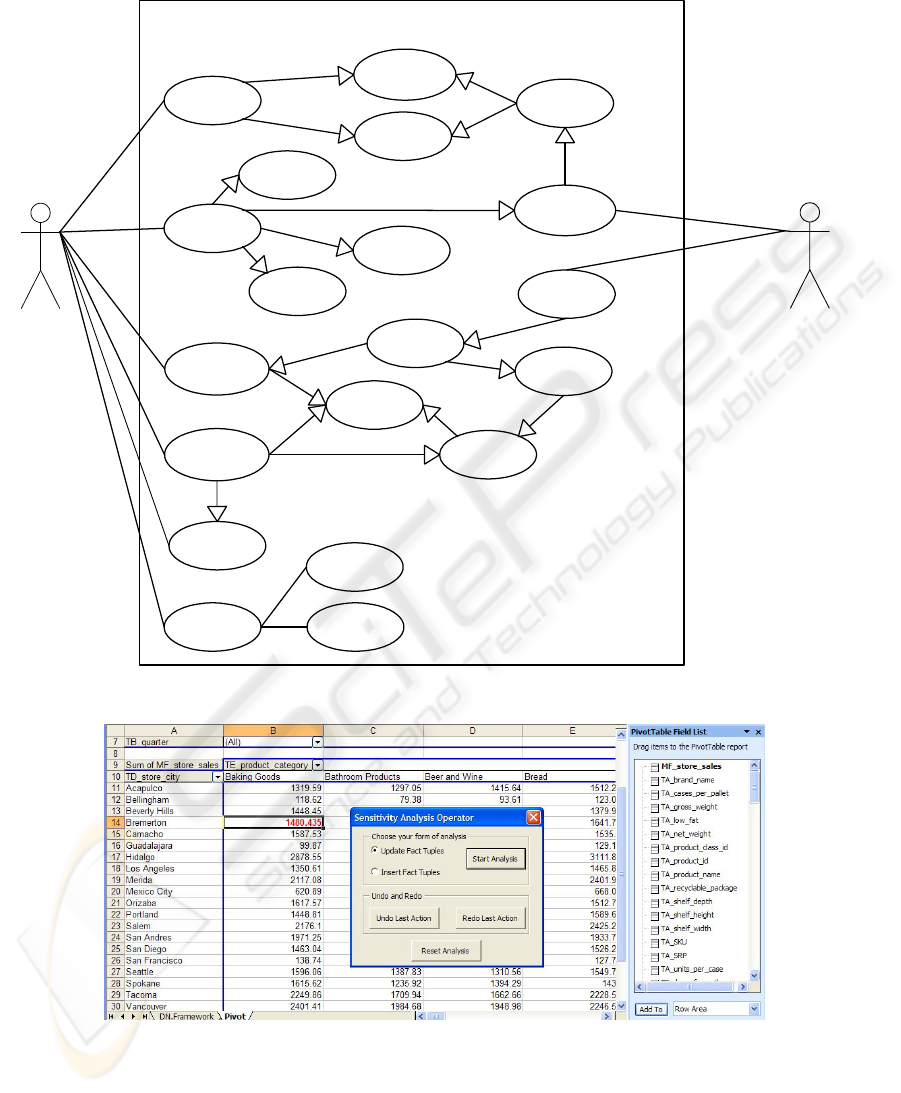
Fig. 2 depicts the UML use case of the program for

OLAP sensitivity analysis and Fig. 3 depicts the

GUI in an MS Excel environment.

For the user it is important to have an interface

that is easy in use. An organized lay-out will help

the user in getting maximum results. Another

important functionality of the prototype is the

dynamic environment. Different databases,

measures, dimensions and tables should all be

handled in an easy consistent manner. With this

dynamic prototype, the most important aspect of the

program, the sensitivity analysis, should not be

forgotten. The user needs a set of tools, which can

be used in order to perform the sensitivity analysis.

Features like the undo operation and error handling,

must also be taken into account. In order to get a

working prototype in Microsoft Excel, some

constraints must be made. The first constraint

applies to the input of the program. The database

must be a Microsoft Access database or some other

database that be accessed with ODBC, that is

modelled via a star schema. From this database, one

single measure can be selected for analysis. In order

to keep the data in the database valid, all sensitivity

analysis operations are done on a copy of the

original database. This makes sure that the original

data will not be modified and the user is able to

‘play’ with the data as much and extreme as he or

she wants. The copy has to be made on the

background without the notice of the user. After

each sensitivity analysis, the selected and changed

cell will be highlighted. From this point, a new

sensitivity analysis can be made by the business

analyst.

6 CONCLUSIONS

In this paper, an extension in the OLAP framework

has been developed and implemented in a prototype

application. The model for sensitivity analysis

describes the theoretical framework of this subject.

The prototype software implementation for

sensitivity analysis is an additional tool for business

analysts that want to analyse their company data

interactively. With this tool, they are able to ‘play’

with the data by doing sensitivity analyses.

ACKNOWLEDGEMENTS

We would like to thank Wim Zuiderwijk and Arno

van den Berg for their contributions to this research.

REFERENCES

E. Caron, H.A.M. Daniels, (2007). Explanation of

exceptional values in multi-dimensional business

databases. European Journal of Operational Research,

188, 884-897.

J. Han and M. Kamber, (2005). Data Mining: Concepts

and Techniques, San Francisco, CA, USA.

H. J. Lenz, A. Shoshani, (1997). Summarizability in

OLAP and statistical data bases, Statistical and

Scientific Database Management, 132–143.

P. A. Samuelson, (1941). The Stability of Equilibrium:

Comparative Statics and Dynamics, Econometrica, 9,

No 2, 97–120.

S. Sarawagi, R. Agrawal, R. Megiddo, (1998). Discovery-

driven exploration of OLAP data cubes, in: Conf.

Proc. EDBT ’98, London, UK, pp. 168–182.

J. R. Schott, (1997). Matrix analysis for statistics.

BUSINESS ANALYSIS IN THE OLAP CONTEXT

329

APPENDIX

Sensitivity Analysis Program

User

Open Database

Select Dimensions

«uses»

Create View

Define Delta

«extends»

«uses»

Select Record

Process Update

Find Records to

Update

«uses»

Create Query

«uses»

Stop Program

Get Base Variables

Create Query

Substract Measure

and Dimensions

«uses»

OLAP Database

Roll-Up

Drill-Down

Slice and Dice

Select Measure

«uses»

«extends»

Perform

Sensitivity Analysis

«extends»

«uses»

«extends»

Close Program

Reset

Undo

«extends»

Figure 2: Use cases for the OLAP sensitivity analysis application.

Figure 3: GUI OLAP sensitivity analysis application.

ICEIS 2009 - International Conference on Enterprise Information Systems

330