Prolegomena toward Algebraic Image Analysis

Igor Gurevich and Vera Yashina

Dorodnicyn Computing Center, Russian Academy of Sciences, Vavilov str. 40

Moscow, 119333 Russian Federation

Abstract. The paper is an extended abstract of analytical tutorial devoted to

algebraization of image analysis.

1 Summary

Automation of image processing, analysis, estimating and understanding is one of the

crucial points of theoretical computer science having decisive importance for

applications, in particular, for diversification of solvable problem types and for

increasing the efficiency of problem solving. The main subgoals are developing and

applying of mathematical theory for constructing image models accepted by efficient

pattern recognition algorithms and for standardized representation and selection of

image analysis transforms. Automation of image-mining is possible by combined

application techniques for image analysis, understanding and recognition.

The specificity, complexity and difficulties of image analysis and estimation (IAE)

problems stem from necessity to achieve some balance between such highly

contradictory factors as goals and tasks of a problem solving, the nature of visual

perception, ways and means of an image acquisition, formation, reproduction and

rendering, and mathematical, computational and technological means allowable for

the IAE.

The mathematical theory of image analysis is not finished and is passing through a

developing stage. It is only recently came understanding of the fact that only

intensive creating of comprehensive mathematical theory of image analysis and

recognition (in addition to the mathematical theory of pattern recognition) could bring

a real opportunity to solve efficiently application problems via extracting from

images the information necessary for intellectual decision making. The transition to

practical, reliable and efficient automation of image-mining is directly dependent on

introducing and developing of mathematical means for IAE.

This work was partially supported by the Russian Foundation for Basic Research Grant № 08-

01-00469, by the project “Algorithmic schemes of descriptive image analysis” of the

Program of Basic Research “Algebraic and Combinatorial Techniques of Mathematical

Cybernetics” of the Department of Mathematical Sciences of the RAS and by the project of

the Program of the Presidium of the Russian Academy of Sciences “Fundamental Problems

of Computer Science and Information Technologies” (the project no. 2.14)

Gurevich I. and Yashina V. (2009).

Prolegomena toward Algebraic Image Analysis.

In Proceedings of the 2nd International Workshop on Image Mining Theory and Applications, pages 3-8

DOI: 10.5220/0001963000030008

 SciTePress

During recent years there was accepted that algebraic techniques, in particular

different kinds of image algebras, is the most prospective direction of construction of

the mathematical theory of image analysis and of development of an universal

algebraic language for representing image analysis transforms and image models.

The purposes of this tutorial are:

• to set forth the state of the art of mathematical theory of image analysis;

• to consider the algebraic approaches and techniques acceptable for image

analysis;

• to present a methodology, mathematical and computational techniques for

automation of image mining on the base of Descriptive Approach to Image Analysis

(DAIA) and to consider an example (automated diagnosis of hematological deceases).

The program of the tutorial is following:

• Introduction «On a way to a unified theory»

The introduction presents a history of image analysis algebraization (M.Duff,

G.Matheron, J.Serra, J.von Neumann, S.Sternberg, S.Unger, and others).

• Chapter 1 “State of the art of mathematical theory of image analysis”.

In the chapter a current state of the mathematical theory of image analysis is

analyzed.

• Chapter 2 “The Algebraic Approaches and Techniques in Image Analysis.

Algebraization of Pattern Recognition (1970 – till now)”.

The chapter considers leading approaches in the mathematical theory of image

analysis oriented for automation of image analysis and understanding.

Chapter 2 consists of the two following sections: 2.1 «The Basic Theories»; 2.2

«Image Algebras».

Section 2.1 «The Basic Theories» describes three basic theoretical approaches in

the field of pattern recognition: 1) “Pattern Theory” (U.Grenander) – techniques for

data representation and transformation on the base of regular combinatorial structures

and algebraic and probabilistic means in pattern recognition; 2) “Theory of

Categories Techniques in Pattern Recognition” (M.Pavel) – formal descriptions of

pattern recognition algorithms via transforms of initial data preserving its class

membership; 3) “The Algebraic Approach to Recognition, Classification and

Forecasting Problems” (Yu.Zhuravlev) – mathematical set-up of a pattern recognition

problem, correctness and regularity conditions, multiple classifiers.

Section 2.2 «Image Algebras» contains a description of two known image

algebras: 1) Standard Image Algebra by G.Ritter – a unified algebraic representation

of image processing and analysis operations; 2) Descriptive Image Algebra by

I.Gurevich – a unified algebraic language for describing, performance estimating and

standardizing algorithms for image analysis, recognition and understanding.

• Chapter 3 “Descriptive Approach to Image Analysis and Understanding

(DAIA) and its main tools”

The chapter describes basic concepts and mathematical tools of DAIA of

I.B.Gurevich and his school (conceptualization of notions for characterizing images

in pattern recognition problems; basic model of image recognition process;

descriptive image models).

Chapter consists of the three following sections: 3.1 “Descriptive Approaches – basic

steps”; 3.2 “DAIA”; 3.3 “Descriptive Image Models”.

Section 3.1 «Descriptive Approaches – basic steps» contains a description of

papers in the field of pattern and image recognition in 1960’s, which gives main

attention to a formal description of initial data, and to a formalization of description

procedures of their transforms (F.Ambler, G.Barrow, R.Burstall, T.Evans, S.Kaneff,

R.Kirsh, R.Narasimhan, A.Rosenfeld, A.Shaw).

Section 3.2 «DAIA» contains a description of basic concepts of DAIA. The main

intention of DAIA is to structure different techniques, operations and representations

being applied in image analysis and recognition. The axiomatic and formal

constructions of DAIA establishes conceptual and mathematical base for representing

and describing images and its analysis and estimation. The DAIA provides an

opportunity to solve the problems connected with the development of formal

descriptions for an image as a recognition object as well as the synthesis of

procedures for an image recognition and understanding. The analysis of the problems

is based on the investigation of inner structure and content of an image as a result of

the procedures “constructing” it from its primitives, objects, descriptors, features and

tokens.

Section 3.3 «Descriptive Image Models (DIM)» contains a description of

mathematical objects providing representation of information carried by an image and

by an image legend (context) in a form acceptable for a recognition algorithm. This

section places high emphasis on multiple DIM and multi-aspect image

representations.

• Chapter 4 “Example”

Chapter “Example” demonstrates application of the descriptive techniques in an

application problem - automating of morphologic analysis of cytological specimens

(lymphatic system tumors).

This chapter consists of the three following sections: 4.1 “Problem set-up”, 4.2

“Mathematical means used for formal representation of a descriptive model of an

information technology for early diagnostic analysis of cytological specimens”; 4.3

“Discussion of the results’.

• Conclusions

The last chapter “Conclusions” discusses open questions of the mathematical theory

of image analysis. Future researches for development of this field are outlined.

The program of the tutorial is briefly presented at Table 1.

Table 1. Tutorial summary.

Name of a Part Content

Introduction

State of the art of mathematical theory of

image analysis.

2.1 The Basic Theories The Algebraic Approaches and Techniques

in Image Analysis. Algebraization of Pattern

Recognition (1970 – till now).

2.2 Image Algebras

Descriptive Approaches

DAIA

Descriptive Approach to Image Analysis and

Understanding (DAIA) and its main tools

Descriptive Image Models

Problem set-up

Mathematical means used for formal

representation of a descriptive model of an

information technology for early diagnostic

analysis of cytological specimens

Example

Discussion of the results

Conclusion

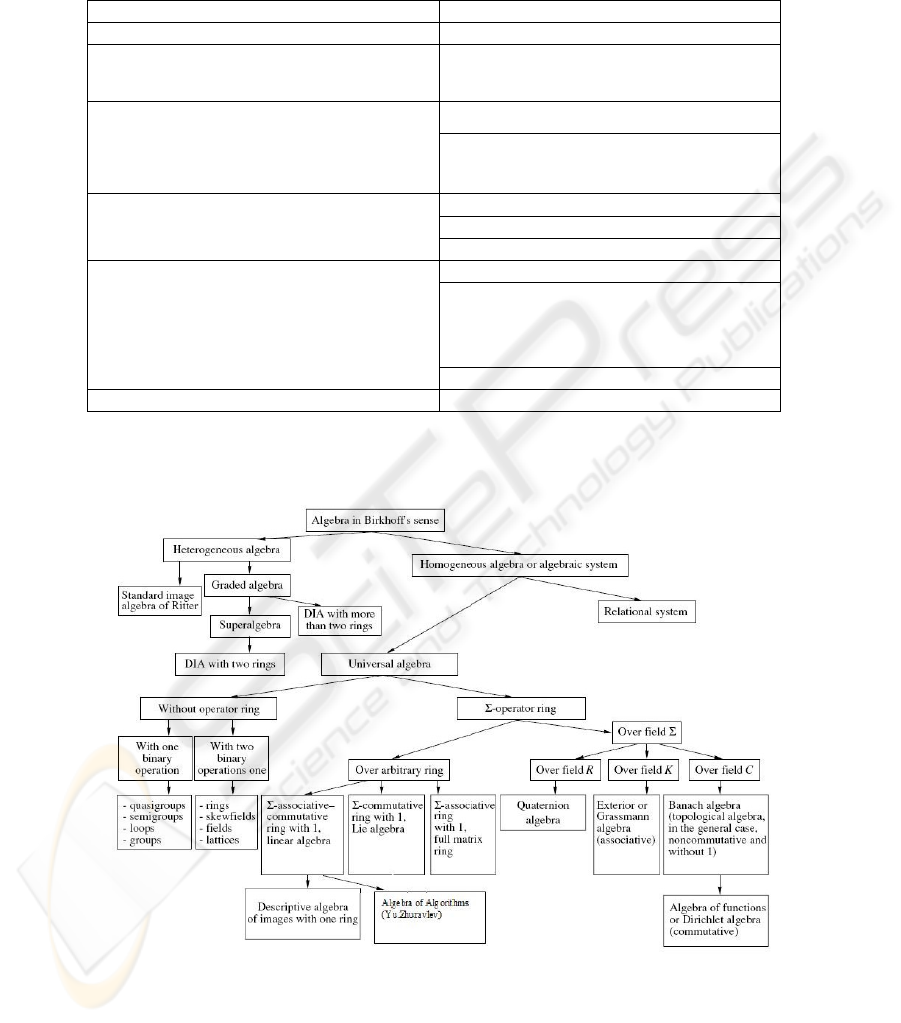
Figure 1 presents a classification reflecting the authors’ point of view on the

contemporary hierarchy of algebras and the place of DIA in this hierarchy.

Fig. 1. Algebraic links.

References

1. Birkhoff, G., Lipson, J. D., Heterogeneous Algebras, Journal of Combinatorial Theory,

Vol.8, 1970, pp. 115-133.

2. T.G. Evans. Descriptive Pattern Analysis Techniques: Potentialities and

Problems//Methodologies of Pattern Recognition (The Proceedings of the International

Conference on Methodologies of Pattern Recognition).- Academic Press, New York,

London, 1969.-pp. 149-157.

3. U. Grenander. General Pattern Theory. A Mathematical Study of Regular Structure.-

Clarendon Press, Oxford, 1993.

4. I.B. Gurevich. Descriptive Technique for Image Description, Representation and

Recognition//Pattern Recognition and Image Analysis: Advances in Mathematical Theory

and Applications in the USSR.- MAIK “Interpreodika”, 1991.-vol. 1- P. 50 – 53.

5. I.B. Gurevich, V.V. Yashina. Generating Descriptive Trees//Proceedings of 10th

International Fall Workshop on Vision, Modeling, and Visualization.- Infix, 2005.-P. 367-

374.

6. Gurevich, I.B., Yashina, V.V., Operations of Descriptive Image Algebras with One Ring.

In Pattern Recognition and Image Analysis: Advances in Mathematical Theory and

Applications. Pleiades Publishing, Inc. 2006. - Vol.16, No.3. - P. 298-328.

7. I.B. Gurevich, V.V. Yashina: Descriptive Approach to Image Analysis: Image Models.

Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applica-

tions, Vol.18, No.4. MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc. (2008) 518-

541.

8. I.B. Gurevich, V.V. Yashina, I.V. Koryabkina, H. Niemann, and O. Salvetti. Descriptive

Approach to Medical Image Mining. An Algorithmic Scheme for Analysis of Cytological

Specimens//Pattern Recognition and Image Analysis: Advances in Mathematical Theory

and Applications. - MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., 2008. -

Vol.18, No.4. - P. 542-562.

9. S.Kaneff. Pattern Cognition and the Organization of Information//Frontiers of Pattern

Recognition (The Proceedings of the International Conference on Frontiers of Pattern

Recognition, ed. Satosi Watanabe).- Academic Press, New York, London.- 1972.-pp. 193-

222.

10. Matheron, G., Random Sets and Integral Geometry, Wiley, New York, 1975.

11. P. Maragos. Algebraic and PDE Approaches for Lattice Scale-Spaces with Global

Constraints//International Journal of Computer Vision, vol.52, no.2/3, Kluwer Academic

Publishers. Manifactured in The Netherlands, 2003.-pp.121-137.

12. D. Marr, Vision, Freeman, New York, 1982.

13. R.Narasimhan. Picture Languages//Picture Language Machines (ed. S.Kaneff).- Academic

Press, London, New York.-1970.-pp. 1-30.

14. Pavel, M. Fundamentals of Pattern Recognition, New York, Marcell, Dekker, Inc., 1989.

15. Ritter, G.X., 2001. Image Algebra. Center for computer vision and visualization,

Department of Computer and Information science and Engineering, University of Florida,

Gainesville, FL 32611.

16. A. Rosenfeld. Picture Languages. Formal Models for Picture Recognition.-Academic Press,

New York, San Francisco, London, 1979.

17. Serra, J.: Image Analysis and Mathematical Morphology. L., Academic Press (1982)

18. A. Shaw. A Proposed Language for the Formal Description of Pictures//CGS Memo. 28,

Stanford University, February.- 1967.

19. Soille,P., Morphological Image Analysis. Principles and Applications (Second Edition). -

Springer-Verlag Berlin Heidelberg, New York, 2003 и 2004.

20. S.R. Sternberg. Grayscale morphology//Computer Vision, Graphics and Image Processing,

vol.35, no.3, 1986.-P. 333-355.

21. Unger, S.H., 1958. A computer oriented toward spatial problems. In Proceedings of the

IRE, 46, - P. 1744-1750.

22. Yu.I. Zhuravlev. An Algebraic Approach to Recognition and Classification

Problems//Pattern Recognition and Image Analysis: Advances in Mathematical Theory and

Applications.- MAIK "Nauka/Interperiodica", 1998.- Vol.8.-P.59-100.