AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE

INTERACTIVE LEARNING OF DATA STRUCTURES

From Algebraic Speciﬁcation to Implementation

Rafael del Vado V

ırseda

Dpto. de Sistemas Inform

aticos y Programaci

on, Universidad Complutense de Madrid, Spain

Keywords:

Virtual learning environments, Virtual universities and classrooms, Learning and teaching methodologies,

Computer supported education, Interactive learning, Data structures, Algorithmic schemes, Algebraic speciﬁ-

cation.

Abstract:

The high level of abstraction necessary to teach “data structures” and “algorithmic schemes” have been more

than a hindrance to students. In order to make a proper approach to this issue, we have developed and imple-

mented, during the last years, at the Computer Science Department of the Complutense University of Madrid,

an innovative interactive learning system according to the new guidelines of the European Higher Education

Area. In this paper, we present the new main contributions to this system. In the ﬁrst place, we describe

the tool called Vedya for the visualization of data structures and algorithmic schemes. In the second place,

the Maude system to execute the algebraic speciﬁcations of abstract data types using Eclipse, by which it is

possible to study from the more abstract level of a software speciﬁcation up to its speciﬁc implementation in

Java, thereby allowing the students a self-learning process.

1 MOTIVATION

The study of “data structures” and “algorithmic

schemes” constitute one of the essential aspects of the

academic formation of every engineer in Computer

Science. Nevertheless, the high level of abstraction

necessary to teach these topics occasionally hinders

its understanding to students. In order to make a

proper approach to this issue, we have developed and

implemented, during the last years, at the Computer

Science Department of the Complutense University of

Madrid, an innovative interactive learning system ac-

cording to the new guidelines of the European Higher

Education Area and the teaching model focused on

the student.

In this paper, we present the two main contribu-

tions to this system. On the one hand, the Vedya tool

(Segura et al., 2008), a visualization tool by means

of which it is possible to provide the student with a

complete learning system of both the main data struc-

tures and the more relevant algorithmic schemes. On

the other hand, the Maude system (Clavel and et al.,

2006) for the execution of “algebraic speciﬁcations”

of abstract data types using the language of formal

speciﬁcation provided by this system.

Thanks to the development environment Eclipse

(http://www.eclipse.org/ ), we have obtained a fully

complete system that is useful for the students as well

as the professors, that allows to go from the most

abstract level of data structures, provided by its al-

gebraic speciﬁcation in Maude, until its speciﬁc im-

plementation in a modern programming language as

happens with Java. All this learning process can be

guided and overseen in a completely autonomous way

by using the Vedya tool, through which it is possible

to make enquiries about the documentation related to

each of the algebraic speciﬁcations, to distinguish bet-

ween the behavior of the structure and its different im-

plementations through the use of different views or to

browse information regarding the cost of the different

implementations that have been proposed.

2 THE VEDYA TOOL

Vedya is an integrated interactive environment for

learning data structures and algorithmic schemes. It

covers the most common data structures: Stacks,

queues, binary search trees, AVL trees, priority

queues, and sorted and hash tables. Moreover, it also

provides other different types of abstract data types,

like one for an implementation of a “doctor’s ofﬁce”.

del Vado Vírseda R. (2009).

AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE INTERACTIVE LEARNING OF DATA STRUCTURES - From Algebraic Speciﬁcation to

Implementation.

In Proceedings of the First International Conference on Computer Supported Education, pages 27-32

DOI: 10.5220/0001844900270032

 SciTePress

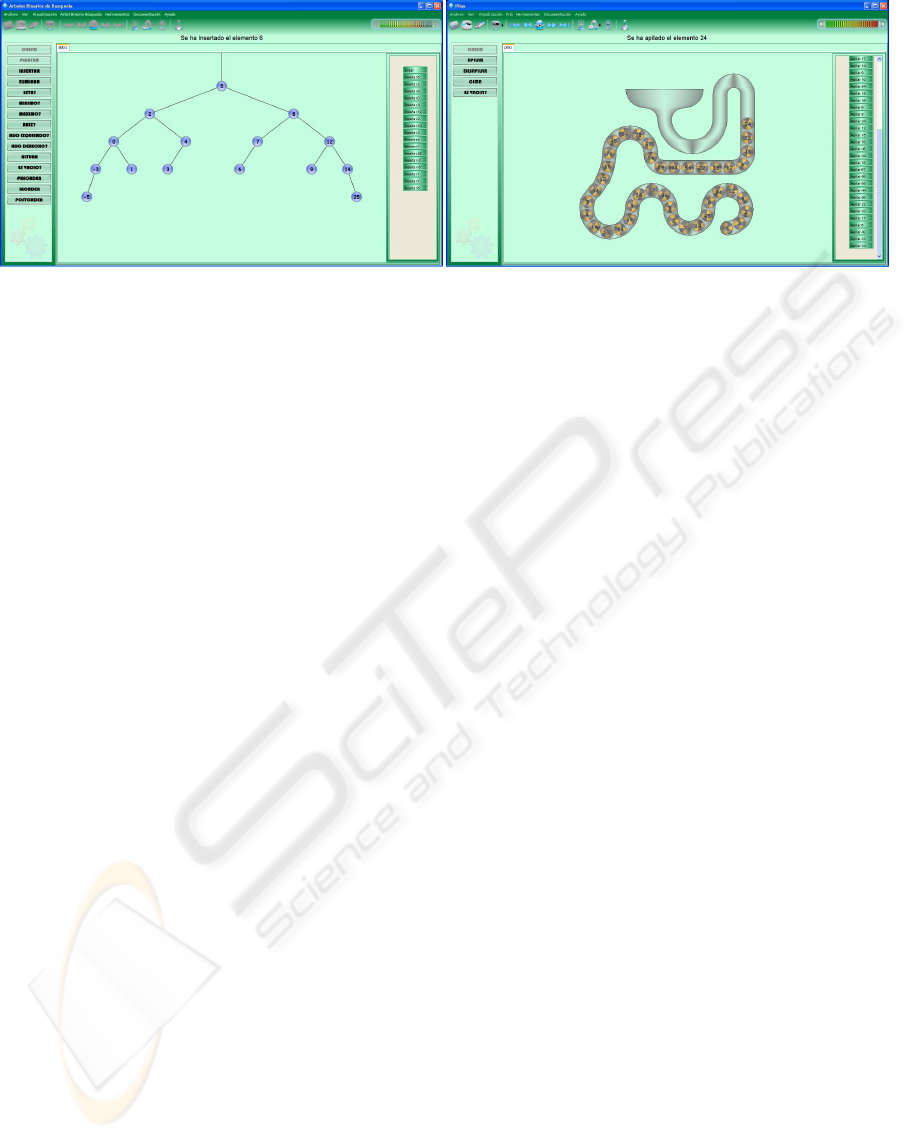
Figure 1: Data structures and algorithmic schemes in the Vedya tool.

Concerning the algorithmic schemes, it covers the

most common resolution methods (Brassard and Brat-

ley, 1996; Cormen et al., 2001; Neapolitan and Naim-

pour, 2003): divide and conquer, dynamic program-

ming, backtracking, and branch and bound. All data

structures and algorithmic schemes taught in the re-

lated study courses are thereby integrated in the same

environment: Vedya allows the execution of different

data structures and several sequences of operations on

the same structures at the same time making use of a

multi-windows and multi-frame system.

Currently, there are two versions of the Vedya tool.

The ﬁrst version contains all the data structures and

algorithmic schemes mentioned above while the new

one offers a subset of them in a more attractive vi-

sual environment. This last version can be found at

http://www.fdi.ucm.es/profesor/rdelvado/.

There are several options to use this tool. The

main one is the interactive execution, but it is also

possible to create simulations that are automatically

executed, to visualize tutorials and to solve tests

within the same environment. It also integrates a set

of animations that show how data structures are used

to solve certain problems. Figure 1 shows an example

of the main windows for data structures (stacks and

binary trees). The central panel is used to represent

the structure. In the case of linear structures and bi-

nary trees, drawing facilities are offered to allow the

expansion or contraction of the data structure or to

move it over the screen to see the hidden parts. On the

left, there is a list of the actions that can be executed.

Partial non-allowed actions are disabled. The right

panel shows the visualization of the actions that have

been already executed. Next, the user may continue

executing actions, go up on the sequence of actions to

see previous states or she/he may use the stimulation

facilities (standard buttons to execute, stop, move for-

ward and move backwards at the top of the screen) to

restart the sequence from the beginning. Notice that

just above the central panel the result of the last action

is shown.

There are two types of views: The one of data

structure behavior to intuitively comprehend its ope-

ration, and one or several implementation views, ei-

ther static or dynamic. On Figure 1 we show the spe-

ciﬁc behavior view of a stack. Representations of the

static implementation based on an array and dynamic

implementation based on pointers can be also shown.

Furthermore, the environment provides documen-

tation about algebraic speciﬁcation, the implementa-

tion code and the cost of each implementation. On the

top of the screen, there is a menu that facilitates mana-

ging the system. We can create a new data structure,

open an existing one or save the state of the editing

one. We can also execute the operations on the data

structure, use the simulation facilities and change the

execution speed of the animations.

The main window for the execution of algorith-

mic schemes looks similar. We have implemented

algorithmic schemes based on divide and conquer

of binary search and quicksort; algorithmic schemes

that solve backtracking problems (in its fractional and

non-fractional version) based on dynamic program-

ming; branch and bound, as well as the Dijkstra algo-

rithm to obtain minimum path in a graph.

As has been previously mentioned, Vedya is

complemented with tutorials on data types (stacks,

queues, binary search trees, red-black trees, prior-

ity queues, and 2-3-4 trees) and animations of algo-

rithms that show the use of a data structure to solve a

problem (evaluation of an expression in postﬁx form,

the transformation of an inﬁx expression to a postﬁx

one, breath-ﬁrst tree transversal, checking of palin-

dromes). Moreover, there are animations on graphs:

To obtain the minimum spanning tree using the Prim

and Kruskal algorithms and to compute minimum

paths using the Dijsktra algorithm.

Finally, Vedya offers the Vedya-Test tool to solve

CSEDU 2009 - International Conference on Computer Supported Education

fmod STACK{X :: TRIV} is fmod QUEUE{X :: TRIV} is

sort Stack{X} . sort Queue{X} .

op error : -> Stack{X} . op error : -> Queue{X} .

op error : -> X$Elt . op error : -> X$Elt .

op empty : -> Stack{X} . op empty : -> Queue{X} .

op push : X$Elt Stack{X} -> Stack{X} . op enqueue : Queue{X} X$Elt -> Queue{X} .

op pop : Stack{X} -> Stack{X} . op dequeue : Queue{X} -> Queue{X} .

op top : Stack{X} -> X$Elt . op first : Queue{X} -> X$Elt .

op isEmpty? : Stack{X} -> Bool . op isEmpty? : Queue{X} -> Bool .

var P : Stack{X} . var C : Queue{X} .

var E : X$Elt . var E : X$Elt .

eq pop(empty) = error . eq dequeue(empty) = error .

eq pop(push(E,P)) = P . ceq dequeue(enqueue(C,E)) = empty if isEmpty?(C) .

eq top(empty) = error . ceq dequeue(enqueue(C,E)) = enqueue(dequeue(C),E))

eq top(push(E,P)) = E . if not isEmpty?(C) .

eq isEmpty?(empty) = true . eq first(empty) = error .

eq isEmpty?(push(E,P)) = false . ceq first(enqueue(C,E)) = E if isEmpty?(C) .

endfm ceq first(enqueue(C,E)) = first(C)

if not isEmpty?(C) .

eq isEmpty?(empty) = true .

eq isEmpty?(enqueue(C,E)) = false

endfm

Figure 2: Algebraic speciﬁcations of stacks and queues in Maude.

tests. This tool can be independently executed

and allows teachers to create, modify or delete

questions in a database, and to create tests from

the database of questions. The student visualizes

the tests, solves them and obtains the correct so-

lutions. Questions are grouped by subject-matter

on the database, but it is possible to mix ques-

tions about different data structures in the same test.

The last version of this tool can be also found at

http://www.fdi.ucm.es/profesor/rdelvado/.

3 EXECUTION OF ALGEBRAIC

SPECIFICATIONS IN MAUDE

For the execution of algebraic speciﬁcations, the lan-

guage Maude (Clavel and et al., 2006) based on

rewriting logic has been used. Maude is a high-

level language and high-performance system support-

ing both equational and rewriting computation for a

wide range of applications. Maude and its formal tool

environment can be used in three mutually reinfor-

cing ways: as a declarative programming language,

as an executable formal speciﬁcation language, and as

a formal veriﬁcation system. Moreover, (Clavel and

et al., 2006) describes the equational speciﬁcation of

the data structures included in the Vedya tool now in

Maude syntax (stacks, queues, lists, binary and search

trees, AVL and 2-3-4 trees). The language is available

for Linux and MacOS at http://maude.cs.uiuc.edu, and

there are also extensions for its execution in Windows

at http://moment.dsic.upv.es.

The speciﬁcations can be executed in Eclipse

(http://www.eclipse.org/ ) by means of special “plug-

ins” developed in the Department of Information Sys-

tems and Computation of the Technical University of

Valencia (DISC-UPV) and in the Computational Lan-

guages and Sciences Department of the University of

alaga (DLCC-UMA). This environment facilitates

the student its usage by integrating the text editor with

the execution commands of the system. On the left,

there appear the developed projects; the central part

shows the editor and the execution panel of the sys-

tem is on it; on the inferior part, the control panel that

shows the result of the action. On the right part, the

user can open other windows that allow the deﬁnition

of different system options and depuration.

The basic element of a speciﬁcation in Maude is

a “module”. The language allows deﬁning the func-

tional modules used to deﬁne the data types; system

modules used to deﬁne rewriting systems and modu-

les focused on objects that allow the usage of syn-

tax of classes, objects and messages. The functional

modules for stacks and queues are showed with more

detail in Figure 2.

The language allows importing other modules,

deﬁning several data types, deﬁning operations on the

types and equations that deﬁne the behavior of those

operations. The modules can be customized, using

“theories” to such end in order to deﬁne the parame-

ters and “views” to relate the formal parameter to the

real parameter. The system has predeﬁned the abstract

data types most commonly used, as well as the most

common theories and views:

AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE INTERACTIVE LEARNING OF DATA

STRUCTURES - From Algebraic Specification to Implementation

view Int from TRIV to INT is

sort Elt to Int .

endv

fmod STACK-INTEGERS is

including STACK{vInt} .

endfm

fmod QUEUE-INTEGERS is

protecting QUEUE{Int} .

endfm

As can be observed, the syntax is similar to the one

used in several texts of algebraic speciﬁcations of data

types (Weiss, 1998).

In order to execute the speciﬁcation, the student

enters the text in the editor; then, she/he executes the

Maude system using the existing buttons in the con-

sole and enters the module. The system detects exis-

ting syntax errors and shows them on the console.

Once the module shows no more errors, the student

may reduce terms by using the equations of the modu-

le. To such end, the student may use the commands

chart placed at the top of the screen or she/he may

directly write the command in the editor and enter it

into the system. For example, in order to obtain the

ﬁrst of a queue, we can reduce the term:

red first(enqueue(enqueue(empty, 5),4)).

This term must be reduced over the module of the

queues using the integer number theory INT. In our

example, this module is named: QUEUE-INTEGERS.

The possibility of reducing terms, in an automatic

way, allows the students to carry out an initial test

of their speciﬁcations by detecting many of the errors

committed when deﬁning the operations using equa-

tions.

Another greater advantage of executing the speci-

ﬁcations is that the student comprehends the diffe-

rence between the parameterized module and the ins-

tantiated module by being able to reduce terms on

different modules. For example, a new module could

be named QUEUE-CHARACTERS on which terms of type

red first(enqueue(enqueue(empty, ’a’),’c’)).

can be easily reduced.

During the last academic courses, we have

done practical classes on the data structures

included in Vedya, which can be found at

http://www.fdi.ucm.es/profesor/rdelvado/.

Other examples of data types, such as “medieval

queues” or a “doctor’s ofﬁce” were also proposed

(Weiss, 1998). In all of them, the aim was to deﬁne

parameterized or instantiated data type with different

theories. The practical classes are complemented with

different terms that the student must reduce over some

type of instantiated modules to prove the speciﬁca-

tion, as well as proposals to make little changes in

some actions or erroneous deﬁnitions to detect them.

Taking into consideration that students from the

second year were involved, just a few of the lan-

guage facilities have been used. In superior courses

where students have more knowledge on the subject,

a richer language can be used (Clavel and et al., 2006)

(e.g., many-sorted equational speciﬁcations, order-

sorted equational speciﬁcations, equational attributes,

and membership equational logic speciﬁcations).

4 FROM SPECIFICATION TO

IMPLEMENTATION

The Vedya tool turns into a pedagogical instrument

of high practical interest since it attempts to address

the whole self-learning process of the main data struc-

tures, from the algebraic speciﬁcation in Maude until

the possible implementations in Java, within such a

powerful and integrated environment as the one that

has been described in the previous section by means

of the Eclipse system.

The students have their ﬁrst contact with the data

structures that they are going to study by means of

the usage of Vedya. For example, if their learning of

data structures is focused on binary search trees or li-

near data structures, they will start learning the corres-

ponding section of the tool, where they will be able to

experiment, freely and on their own, each one of the

actions offered by these structures (see Figure 1). In

order to strengthen and evaluate this intuitive know-

ledge, the student has, in addition, the possibility of

using the Vedya-Test tool.

Once the student has a clear idea of the informal

behavior of the data structure, she/he may start work-

ing on the Eclipse system. The ﬁrst step would be: to

formally capture that intuitive knowledge she/he has

obtained through the usage of Vedya in a speciﬁc al-

gebraic speciﬁcation written in Maude syntax. In or-

der to facilitate this difﬁcult step in the student’s self-

learning, she/he may use, interactively, the documen-

tation that is included in the manual of the Vedya tool.

Once the speciﬁcation (see Figure 2) is entered into

the Eclipse system, the student can now go on exe-

cuting little tests using Maude, in order to check

whether it coincides with the intuitive and informal

notion of data structure from which he initially de-

parted in Vedya. Such experience would allow the

student to reach the high level of abstraction that is

necessary in computer supported education for each

formal speciﬁcation of a software component, always

based on the intuitive and experimental knowledge.

CSEDU 2009 - International Conference on Computer Supported Education

Stacks 1 Stacks 2 Queues Sequences BST AVL RB Heaps

Group A (130) 76.4% 82.5% 77.8% 65.6% 82.2% 84.9% – 86.3%

Group B (59) 78.9% 83.6% 85.0% 63.6% 86.2% 87.7% 90.9% 90.2%

Group C (131) 76.2% 79.8% 73.5% 69.0% 83.5% – 68.9% 86.8%

2002/03 2003/04 2004/05 2005/06 2006/07 2007/08

Not attended 57.6% 45.3% 42.3% 64.7% 50.8% 40.2%

Passed 15.3% 22.2% 20.2% 18.2% 30.1% 42.6%

Failed 27.1% 32.5% 37.5% 17.1% 18.9% 17.2%

Figure 3: Students answering the tests and percentage of correct answers.

Once the algebraic speciﬁcation of the data struc-

ture is obtained, the next step would be to develop an

implementation in an object-oriented programming

language such as Java, by means of the facilities pro-

vided by the programming environment in Eclipse.

This time, the student may use the algebraic speciﬁca-

tion that she/he has built, as if dealing with an authen-

tic “instructions manual”. The main advantage of our

methodology is that the speciﬁcation behaves now as

a prototype of the data structures to be implemented,

in a way that the student is able to ﬁnd out the ex-

act behavior for all those moments of doubt that may

appear during the design process, even before she/he

is able to compile the program. In order to be able to

guide, in a more speciﬁc way, the step of speciﬁcation

to implementation, the student may make use again of

the Vedya tool. This time, the student may access to

the part that would correspond with the implementa-

tion of data structure that she/he is studying from the

options menu (see Figure 1). From there, she/he may

try different implementation possibilities based on ar-

rays or pointers.

Once the student is familiar with the different im-

plementations of the structure, she/he is ﬁnally ready

to properly decide on a suitable representation in the

Java language. The possibility of having understood

and previously evaluated the different implementa-

tions by means of Vedya allows the student the possi-

bility to acquire a clear knowledge of the algorithmic

cost of the chosen implementation in Java for each

speciﬁc operation of the data structure, so that this

would also be a decisive criterion at the moment of

designing its own implementations. In this part, the

“algorithmic schemes” part of the Vedya tool plays an

important role, since it allows the student to acquire a

good programming methodology.

5 EVALUATION

In order to obtain a detailed evaluation of the usage of

Vedya and Maude in our integrated system, we have

proposed several tests related to the behavior, speci-

ﬁcation, implementation and application of the main

data structures offered by the tool. We also collect stu-

dents’ opinion using Vedya in the “Data Structures”

academic subject at the second year, and in the “Pro-

gramming Methodology and Technology” subject at

the third year, respectively.

The vast majority of our engineering and com-

puter science students have taken an introductory pro-

gramming course in the ﬁrst academic year, typically

in Pascal. Although the learning of the main algo-

rithmic schemes and programming techniques is not a

prerequisite to the subject of “Data Structures”, many

students choose to take it either prior to, or concur-

rent with, “Programming Methodology and Techno-

logy”. As a result, although a pseudocode program-

ming language is the assumed language for “Data

Structures”, many students have enough knowledge

about C++ or Java programming languages through

the integrated programming laboratories of parallel

academic courses and subjects.

Taking into account this proﬁle, skills and back-

ground of our engineering and computer science

students, we have proposed 8 tests in the Virtual

Campus of the Complutense University of Madrid

(http://www.ucm.es/campusvirtual/CVUCM/). The

number of engineering students registered in the Vir-

tual Campus was just over 320 distributed in three

groups (130 in group A, 59 in group B, and 131 in

group C). Figure 3 shows the number of the students

who answered each of the tests in the corresponding

group.

We observe that, from the second test on, the num-

ber of students becomes stable in a number lightly low

to the number of students who access regularly to the

Virtual Campus. These numbers, though seemingly

high, are only between 23 % (75 students of 320) and

AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE INTERACTIVE LEARNING OF DATA

STRUCTURES - From Algebraic Specification to Implementation

37 % (118 of 320) of registered students, which shows

the high rate of students giving up in this topic from

the beginning.

Figure 3 also shows the percentage of correct ans-

wers in the three groups: In general, it is high, which

demonstrates the interest of the students who have

taken part. In group B, the percentage is slightly

higher than groups A and C; since 85 % of the stu-

dents who have decided to complete the tests across

the Virtual Campus of group B are not “new” students

of this academic subject.

Figure 3 shows the percentage of students that did

not attend the ﬁnal exam, those who passed, and those

who failed during the last six years. We observe that

in the last academic courses, in which we have ap-

plied the Vedya tool, we have reduced by 14% the

percentage of students giving up the course with res-

pect to the previous course, and at the same time,

we have increased by 12% the percentage of students

that passed the exam. The percentage of students that

failed the exam increased by 2% due to the rise of

students attending the exam. Comparing with previ-

ous courses (2003 to 2004) the percentage of students

that passed has increased between 8% (with respect

to the course 2003/04) and 15% (with respect to the

course 2002/03).

6 CONCLUSIONS

In this paper, we have described the usage of an in-

novative educational environment for the interactive

learning of data structure and algorithmic schemes by

means of the visualization tool called Vedya and the

speciﬁcation language Maude with its programming

environment in the Eclipse system.

In the last years, many papers on visualization of

data structures and algorithms have been written. For

example, a tool with a similar style is presented in

(Chen and Sobh, 2001). Nevertheless, there is a lack

in many of them of a graphic user interface of data

structures and algorithms or they can only be executed

in a few operative systems. In this sense, Vedya is

something more than a simple tool for the execution

of data structure as has been shown in Section 2 and

(Segura et al., 2008).

The application of Vedya and Maude in a com-

plete system as Eclipse allows the students the possi-

bility of acquiring the capacity of implementing, cor-

rectly and properly, a data structure according to its

formal algebraic speciﬁcation, using in their design,

the proper algorithmic schemes. As a consequence, it

is possible to provide the students with a complete

and professional methodology of software develop-

ment that is very useful in the current teaching of

Computer Science.

During the academic courses 2006/07 and

2007/08, we have carried out a detailed study in class-

room on the application of this innovative educational

environment by the Virtual Campus of the Com-

plutense University of Madrid, in the “Data Struc-

ture” and “Programming Methodology and Techno-

logy” courses corresponding to the second and third

academic courses of Computer Science.

As future work, we plan to design an Intelligent

Tutoring System in order to guide the interactive self-

learning process of data structures from the algebraic

speciﬁcation to the real implementation.

ACKNOWLEDGEMENTS

This work has been partially supported by the Spanish

National Projects FAST-STAMP (TIN2008-06622-

C03-01), MERIT-FORMS (TIN2005-09027-C03-03)

and PROMESAS-CAM (S-0505/TIC/0407).

REFERENCES

Brassard, G. and Bratley, P. (1996). Fundamentals of algo-

rithms. Prentice Hall.

Chen, T. and Sobh, T. (2001). A tool for data structure

visualization and user-deﬁned algorithm animation. In

Frontiers in Education Conference.

Clavel, M. and et al. (2006). All about maude. A high per-

formance logical framework. In How to Specify, Pro-

gram and Verify Systems in Rewriting Logic, LNCS.

Springer.

Cormen, T., Leiserson, C., Rivest, R., and Stein, C. (2001).

Introduction to Algorithms. The MIT Press.

Neapolitan, R. and Naimpour, K. (2003). Foundations of al-

gorithms using C++ pseudocode. Jones and Bartlett.

Segura, C., Pita, I., del Vado, R., Saiz, A. I., and Soler,

P. (2008). Interactive Learning of Data structures and

algorithmic schemes. In ICCS, volume 5101 of LNCS,

pages 800–809. Springer.

Weiss, M. (1998). Data Structures and Problem Solving

Using Java. Addison-Wesley.

CSEDU 2009 - International Conference on Computer Supported Education