
SCORING OF BREAST TISSUE MICROARRAY SPOTS
THROUGH ORDINAL REGRESSION
Telmo Amaral, Stephen McKenna
School of Computing, University of Dundee, Dundee, U.K.
Katherine Robertson and Alastair Thompson
School of Medicine, University of Dundee, Dundee, U.K.
Keywords:
Breast tissue microarrays, Scoring, Immunohistochemistry, Ordinal regression.
Abstract:
Breast tissue microarrays (TMAs) facilitate the study of very large numbers of breast tumours in a single
histological section, but their scoring by pathologists is time consuming, typically highly quantised, and not
without error. This paper compares the results of different classification and ordinal regression algorithms
trained to predict the scores of immunostained breast TMA spots, based on spot features obtained in previous
work by the authors. Despite certain theoretical advantages, Gaussian process ordinal regression failed to
achieve any clear performance gain over classification using a multi-layer perceptron. The use of the entropy
of the posterior probability distribution over class labels for avoiding uncertain decisions is demonstrated.
1 INTRODUCTION
Tissue microarrays (TMAs) are a high-throughput
technique proposed by Kononen (Kononen et al.,
1998), to facilitate the study of large numbers of tis-
sue samples on a single histological section; a TMA
section contains hundreds of small spots of tissue ar-
ranged in a grid-pattern. TMAs are now extensively
utilised in the study of cancers. TMAs are constructed
by taking cylindrical biopsies (named cores) from
donor blocks of formalin fixed wax embedded tissue
(tumour or normal) and inserting them into a recipi-
ent wax block in a grid arrangement. Sections of the
TMA block are cut and provide targets for parallel
in situ detection of DNA, RNA, and protein targets
in each specimen on the array. Every TMA section
contains an array of spots of tissue, each spot being
a section of one of the cores previously inserted into
the microarray block. Consecutive sections allow the
rapid analysis of hundreds of molecular markers in the
same set of specimens on only a few histological sec-
tions. Camp (Camp et al., 2000) concluded that two
cores per patient are sufficient to adequately represent
the expression of three common antigens in invasive
breast carcinoma.
Immunohistochemistry is carried out to detect
protein expression in the tissue spots. For example,
antibodies directed against progesterone receptor can
be used to detect nuclear expression of progesterone
receptor in breast tumours. Once immunohistochem-
istry is carried out, the assessment by pathologists of
the stained breast TMA sections starts with the clas-
sification of each tissue spot. In our experience, the
spots are usually one of several types, namely: tu-
mour, normal, stroma, fat, blood, or invalid (no spot
present or spot un-assessable). This initial classifi-
cation must be carried out prior to assessing the im-
munostaining (level of expression of the protein of
interest, e.g. progesterone receptor) due to the fact
that the donor cores embedded in the TMA are not
always homogeneous throughout their length; there
may be tumour in the top third of the core, but the
remainder of the core may be stroma. Therefore, to
ensure correct analysis, each tissue spot on the TMA
section should first be classified as to the type of tis-
sue present. The degree of immunostaining is then as-
sessed and assigned a score. Once all of the spots have
been scored, the scores can be compared. Applying
this procedure to breast TMA sections incorporating
large numbers of tissue samples is time consuming
and suffers from inter- and intra-observer variability,
perceptual errors, and severe quantisation that leads
to the loss of potentially valuable information. Thus,
there is strong motivation for the development of au-
243
Amaral T., McKenna S., Robertson K. and Thompson A. (2009).
SCORING OF BREAST TISSUE MICROARRAY SPOTS THROUGH ORDINAL REGRESSION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 243-248
DOI: 10.5220/0001808202430248
Copyright
c
SciTePress

tomated methods for quantitative analysis of breast
TMA image data.
Most of the published work on automated “rank-
ing” of breast tissue sections aims not at pre-
dicting immunohistochemical scores, but rather at
distinguishing between different Bloom-Richardson
grades, given tissue sections stained solely with
Hematoxylin & Eosin. Petushi (Petushi et al., 2006)
used supervised learning (namely linear, quadratic,
neural network, and decision tree classifiers) to dis-
tinguish low, intermediate, and high grades of histol-
ogy slides, based on tissue texture parameters derived
from spatial information on cell nuclei distribution.
Axelrod (Axelrod et al., 2008) performed step-wise
forward Cox regressions with clinical and pathologi-
cal factors and image features describing nuclear mor-
phometry, densitometry, and texture, to distinguish
low, intermediate, and high worst grades. More re-
cently, Doyle (Doyle et al., 2008) used a support vec-
tor machine (SVM) to distinguish low and high grades
from digitised histopathology, based on textural and
nuclear architecture features. Additional recent work
on nuclear grading has been published by Chapman
(Chapman et al., 2007), Dalle (Dalle et al., 2008), and
Zhang (Zhang et al., 2008). In contrast, Kostopoulos
(Kostopoulos et al., 2007) applied k-nearest neigh-
bour weighted votes classification to colour-textural
features, in order to predict the oestrogen receptor’s
(ER) positive status of biopsy images, traditionally
assessed via a scoring protocol that takes into ac-
count the percentage of epithelial nuclei that are im-
munopositive.
In this paper, we compare the results of ordi-
nal regression and classification algorithms trained
to predict the immunoscores of breast TMA spots.
Ordinal regression differs from classification in that
the existence of an order between the different cat-
egories is taken into account. So, in the prediction
of tumour scores, ordinal regression should in prin-
ciple achieve better results than classification. We
trained neural network classifiers and ordinal regres-
sion algorithms based on Gaussian processes to pre-
dict the Quickscores (Detre et al., 1995) of breast
TMA spots subjected to progesterone receptor im-
munohistochemistry which results in nuclear staining
in positive cases. A Quickscore is composed of two
integer values, namely a value between 0 and 6 that
estimates the proportion of epithelial nuclei that are
immunopositive, and a value between 0 and 3 that es-
timates the strength of staining of those nuclei (these
values will henceforth be referred to as QSP and QSS,
respectively). In our experiments, each spot is charac-
terised by two features obtained in previous work by
the authors, derived from colour and texture features
of pixels, as summarised in section 2.
The remainder of this paper is organised as fol-
lows. Section 3 provides an overview of the data and
algorithms. Section 4 describes the experiments car-
ried out and presents their results. Section 5 discusses
the results and section 6 presents some conclusions
and recommendations.
2 PREVIOUS WORK
Our previous work included the classification of
breast-TMA spots into two classes, as to the pres-
ence or absence of immunopositive epithelial nu-
clei (regardless of the type of spot) (Amaral et al.,
2008). The analysed data consisted of 110 spots (2
for each of 55 participants) subjected to progesterone-
receptor (PR) nuclear staining and whose immunos-
tates (positive or negative) were assigned by a pathol-
ogist. In addition, the contours of several hundred ep-
ithelial nuclei were marked within randomly selected
sub-regions and labelled as immunopositive or neg-
ative. In a first stage, the pixels within annotated
sub-regions were used to estimate the likelihoods of
RGB and differential invariant features (computed for
two scales up to the 2nd order) for three classes,
namely: epithelial positive, epithelial negative, and
background. Assuming these features to be inde-
pendent, their likelihoods were then used to classify
the pixels of whole spots into the three considered
classes, using Bayes’ rule. In a second stage, the pre-
viously classified pixels were used to compute fea-
tures for each spot that aimed to formalise the two
Quickscore values assigned by pathologists. A gener-
alised linear model (GLM) was then trained to clas-
sify spots as to their immunostate, based on the two
computed features. A leave-2-out experiment was
carried out, in order to assess the ability of the sys-
tem to deal with data from new participants. Differ-
ent combinations of features were tested, leading to
the conclusion that the use of differential invariants in
addition to colour yielded a small improvement in ac-
curacy. The most favourable combination of features
resulted in a correct-classification rate of 84%.
3 MATERIALS AND METHODS
3.1 Data
The data used in this work consist of two features
(extracted as described previously in section 2) char-
acterising each of 190 breast TMA spots of normal
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
244

or tumour tissue subjected to progesterone receptor
(PR) nuclear staining, along with the Quickscore val-
ues assigned to those spots by a pathologist. The digi-
tised TMA slides originate from the National Cancer
Research Institute’s Adjuvant Breast Cancer (ABC)
Chemotherapy Trial (Adjuvant Breast Cancer Trials
Collaborative Group, 2007).
3.2 Algorithms
Two types of neural networks were trained to classify
spots into their QSP and QSS values, namely single-
layer networks (also called generalised linear models,
or GLMs) and two-layer networks (also called multi-
layer perceptrons, or MLPs) (Bishop, 2006). The
GLMs were trained through the iterated re-weighted
least squares (IRLS) algorithm. The learning al-
gorithm used with the MLPs was scaled conjugate-
gradients (SCG) optimisation. For both types of net-
work, softmax was chosen as the activation function.
The Netlab (Nabney, 2002) implementations of the
GLM and the MLP were used.
For the prediction of QSP and QSS values through
ordinal regression, we employed the Gaussian process
techniques reported by Chu (Chu and Ghahramani,
2005), briefly summarised in the following. Consid-
ering a data set composed of n samples, where the
ith sample is a pair of input vector x
i
∈ R
d
and target
y
i
∈ {1, 2, ..., r} (without loss of generality). Gaussian
processes assume each x
i
to be associated with an un-
observable latent function f (x
i
) ∈ R (a zero-mean ran-
dom variable), on which the ordinal variable y
i
in turn
depends. The process is specified by the covariance
matrix for the set of functions, whose elements can
be defined by Mercer kernel functions. In this work,
we used two types of kernel, namely a linear kernel
and a Gaussian kernel, as defined in equations 1 and
2, respectively.
Cov[ f (x
i
), f (x
j
)] = κ
o
∑
κ
a
x
ς
i
x
ς
j
(1)
Cov[ f (x
i
), f (x
j
)] = κ
o
exp(−
κ
a
2
d
∑
ς=1
(x
ς
i
− x
ς
j
)
2
) (2)
Every Gaussian process has a number of hyper-
parameters that need to be optimised, such as κ
o
and
κ
a
in the formulas above. In this work, for each
type of kernel, two Bayesian techniques were used for
hyper-parameter learning, here referred to simply as
maximum a posteriori estimate (MAP) and expecta-
tion propagation (EP). We used the Gaussian process
algorithms made available by Chu (Chu and Ghahra-
mani, 2005).
Along with the predicted score for each spot, both
the classification and ordinal regression algorithms
output r real values that can be interpreted as the
posterior probabilities of the spot belonging to each
score. As discussed later in section 5, this type of out-
put proved to be useful.
The batch code used to run the experiments and
process their results was implemented in Matlab.
4 EXPERIMENTS AND RESULTS
Leave-one-out experiments were carried out to pre-
dict the QSP and the QSS values of the 190 available
spots, for the classification and ordinal regression al-
gorithms described previously in section 3. For each
value type (QSP and QSS), two types of experiment
were carried out. In the first case, the models were
trained to predict raw Quickscore values. These ex-
periments are referred to as Raw in table 1. In the
second case, the models were trained to predict col-
lapsed Quickscore values, obtained from the raw val-
ues as shown in equations 3 and 4. These experiments
are referred to as Collapsed in table 1. In addition, the
raw predicted values resulting from the first case were
collapsed a posteriori, so as to be comparable with
those resulting from the second case. These modified
results are referred to as Raw c.a.p. in table 1.
v
QSP.collapsed
=
0 if v
QSP.raw
= 0
1 if v
QSP.raw
∈ {1, 2}
2 if v
QSP.raw
∈ {3, 4}
3 if v
QSP.raw
∈ {5, 6}
(3)
v
QSS.collapsed
=
0 if v
QSS.raw
= 0
1 if v
QSS.raw
∈ {1, 2}
2 if v
QSS.raw
= 3
(4)
Chu (Chu and Ghahramani, 2005) reported results
for various data sets and algorithms, to support the
comparison between algorithms. The result reported
for each experiment consists of the mean absolute er-
ror (i.e. the average deviation of the prediction from
the true target) over all test samples, along with the
standard deviation of partial mean absolute errors.
Each partial error is computed over the test samples
included in a given random partition of the data. For
each data set, a number of random partitions is de-
fined. A standard deviation computed in this way,
however, has the disadvantage of depending on the
partitioning of the data (specifically, on the number
of test samples per partition). In our work, for each
experiment, we chose to compute the mean and stan-
dard deviation of the absolute error over all samples.
These values are presented in table 1, the best results
on each row being typed in boldface.
SCORING OF BREAST TISSUE MICROARRAY SPOTS THROUGH ORDINAL REGRESSION
245

Table 1: Means and standard deviations of the absolute errors yielded by the various experiments.
Target QS value Algorithm
Netlab Gaussian process ordinal regression
GLM MLP MAP EP
Lin. Gau. Lin. Gau.
P Raw 1.400 ±1.677 0.926 ±1.215 1.126 ±1.397 0.921 ±1.172 0.900 ±1.129 0.888 ±1.175
P Raw c.a.p. 0.774 ±0.935 0.516 ±0.733 0.626 ±0.805 0.537 ±0.702 0.500 ±0.680 0.503 ±0.698
P Collapsed 0.684 ±0.870 0.432 ±0.677 0.579 ±0.757 0.426 ±0.619 0.463 ±0.639 0.426 ±0.611
S Raw 0.937 ±1.097 0.763 ±0.988 0.937 ±1.106 0.784 ±1.003 0.800 ±1.025 0.779 ±0.994
S Raw c.a.p. 0.674 ±0.727 0.547 ±0.655 0.663 ±0.729 0.558 ±0.662 0.568 ±0.677 0.553 ±0.655
S Collapsed 0.589 ±0.626 0.495 ±0.589 0.526 ±0.606 0.495 ±0.561 0.489 ±0.589 0.489 ±0.561
For each experiment, besides the values reported
in table 1, a confusion matrix was computed. The
matrices for some of the experiments are shown in
Table 2.
0 0.5 1 1.5 2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
entropy threshold
(66)-qs-s-c-be-gpor-ep--gau
proportion of spots
mean absolute error
a) QSS Collapsed, EP Gau
0 0.5 1 1.5 2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
entropy threshold
(96)-qs-p-c-be-gpor-ep--gau
proportion of spots
mean absolute error
b) QSS Collapsed, EP Gau
Figure 1: Fraction of processed spots, and mean absolute er-
ror over those spots, versus confidence threshold, for two of
the experiments (lower entropy means higher confidences.
As mentioned previously in section 3, all of the
employed algorithms output, along with each predic-
tion, a posterior probability distribution over the r
targets. The entropy of a posterior distribution can
be used as a simple measure of classification or or-
dinal regression confidence (the lower the entropy,
the higher the confidence). For two of the experi-
ments, figure 1 shows the fraction of test spots that
can be predicted below a given entropy threshold.
Also shown is the mean absolute error computed over
each fraction of spots.
5 DISCUSSION
Models trained to predict collapsed Quickscore values
consistently yielded better mean absolute errors than
models trained to predict the same Quickscores in raw
format (collapsed only a posteriori for the purpose
of comparison). This difference in quality of the re-
sults was also reflected in the confusion matrices. All
matrices for the prediction of raw Quickscores (QSPs
or QSSs, regardless of the algorithm) showed one or
two middle targets with zero predictions, but this ef-
fect was not observable in the matrices for the predic-
tion of collapsed Quickscores. To illustrate this, ta-
bles 2(a) and (b) show the matrices for the prediction
of raw and collapsed QSPs, respectively, via the EP
algorithm with Gaussian kernel; and tables 2(c) and
(d) show the matrices for the prediction of QSSs via
MLP and EP with Gaussian kernel, respectively. This
may indicate a lack of training examples for middle
targets, or inadequacy of the features used to charac-
terise TMA spots, or even that the number of scoring
ordinals used in practice is excessive.
The GLM algorithm performed poorly. Besides
yielding the highest mean absolute error in every ex-
periment, the prediction of collapsed QSPs yielded a
confusion matrix that showed a middle target with no
predictions, something that did not happen with any
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
246
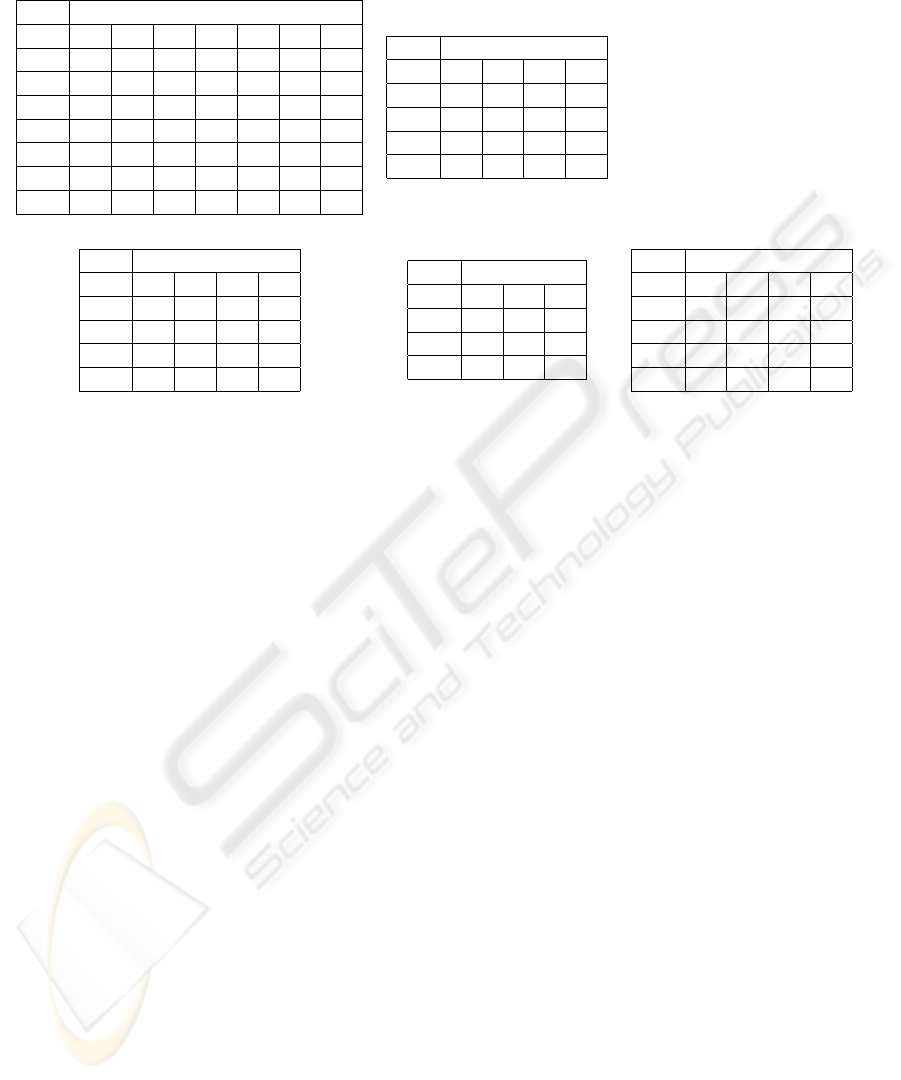
Table 2: Confusion matrices for some of the experiments.
(a) QSP Raw, EP, Gau (b) QSP Collapsed, EP, Gau.
Test Predicted
0 1 2 3 4 5 6
0 65 00 04 00 01 00 00
1 16 00 02 00 00 00 00
2 13 00 08 00 03 00 01
3 03 00 08 00 04 03 00
4 04 00 04 00 04 04 02
5 03 00 03 00 02 01 07
6 00 00 01 00 00 04 17
Test Predicted
0 1 2 3
0 59 11 02 00
1 21 15 06 01
2 03 09 18 07
3 01 03 06 28
(c) QSS Raw, MLP (d) QSS Collapsed, EP, Gau (e) QSP Collapsed, GLM
Test Predicted
0 1 2 3
0 68 00 00 04
1 15 00 00 16
2 08 00 00 29
3 13 00 02 35
Test Predicted
0 1 2
0 52 20 00
1 16 28 24
2 06 21 23
Test Predicted
0 1 2 3
0 65 00 03 04
1 39 00 02 02
2 19 00 09 09
3 05 00 05 28
other algorithm. This matrix is shown in table 2(e).
Ordinal regression with EP and Gaussian kernel
could be said to be the best algorithm, based solely
on the mean absolute errors. It yielded an error that
was always either the lowest or very close to the low-
est. However, the large values of the absolute error’s
standard deviation shown in table 1 seem to render a
comparison between algorithms inconclusive.
It should also be noted that the MLP algorithm
performed surprisingly well, when compared with the
ordinal regression methods. This suggests that further
research to improve the ordinal regression method is
needed, given the expectation that formulating the tis-
sue scoring problem as ordinal regression should rep-
resent an advantage over classification. A possibil-
ity would be to investigate modifications to the ordi-
nal regression algorithms that could model the way
in which pathologists mislabel the ground-truth. The
MLP also consumed a computational time per TMA
spot that is is at least one order of magnitude below
that taken by the ordinal regression (tenths of second
versus several seconds).
As the entropy threshold set on the predic-
tions was decreased (i.e., as the minimum confi-
dence threshold is increased), the mean absolute error
tended to decrease, as exemplified in Figures 1(a) and
(b). This suggests that it is possible to automatically
process, with quite low mean errors, reasonable frac-
tions of spots that are more unequivocal, while iden-
tifying the more difficult spots that cannot dispense
with human assessment.
6 CONCLUSIONS
AND RECOMMENDATIONS
This paper compared the results of ordinal regres-
sion and classification algorithms trained to predict
the scores of breast tissue sections. Purely in terms
of mean absolute errors, ordinal regression via EP
with Gaussian kernel yielded the best results in most
experiments, but the MLP classifier’s performance is
practically at the same level. The reasons behind this
should be further investigated. In turn, GLM was
found to perform poorly. Models trained to predict
collapsed ordinal targets achieve considerably better
results than models trained to predict raw targets (col-
lapsed only a posteriori for comparison). It would be
interesting to further investigate this limitation, too.
By setting confidence thresholds, it should be pos-
sible to use the methods discussed in this paper to
process reasonable fractions of spots with low mean
absolute errors. Future work should also investigate
how to take into account the costs of different kinds
of error (e.g. predicting a score of 2 as 1 should in
principle have a lower cost than predicting a 1 as 0),
and build those into the ordinal regression model.
REFERENCES
Adjuvant Breast Cancer Trials Collaborative Group (2007).
Polychemotherapy for early breast cancer: Re-
sults from the international adjuvant breast cancer
SCORING OF BREAST TISSUE MICROARRAY SPOTS THROUGH ORDINAL REGRESSION
247

chemotherapy randomized trial. Journal of the Na-
tional Cancer Institute, 99(7):506–515.
Amaral, T., McKenna, S., Robertson, K., and Thompson,
A. (2008). Classification of breast-tissue microarray
spots using colour and local invariants. In IEEE In-
ternational Symposium on Biomedical Imaging: From
Nano to Macro, pages 999–1002, Paris, France. IEEE.
Axelrod, D., Miller, N., Lickley, H., Qian, J., Christens-
Barry, W., Yuan, Y., Fu, Y., and Chapman, J. (2008).
Effect of Quantitative Nuclear Image Features on Re-
currence of Ductal Carcinoma In Situ (DCIS) of the
Breast. Cancer Informatics, 4:99–109.
Bishop, C. M. (2006). Pattern Recognition and Ma-
chine Learning (Information Science and Statistics).
Springer-Verlag New York, Inc., Secaucus, NJ, USA.
Camp, R., Charette, L., and Rimm, D. (2000). Validation
of tissue microarray technology in breast carcinoma.
Laboratory Investigation, 80(12):1943–1949.
Chapman, J., Miller, N., Lickley, H., Qian, J., Christens-
Barry, W., Fu, Y., Yuan, Y., and Axelrod, D. (2007).
Ductal carcinoma in situ of the breast (DCIS) with
heterogeneity of nuclear grade: prognostic effects of
quantitative nuclear assessment. BMC Cancer, 7:174.
Chu, W. and Ghahramani, Z. (2005). Gaussian processes
for ordinal regression. Journal of Machine Learning
Research, 6:1019–1041.
Dalle, J., Leow, W., Racoceanu, D., Tutac, A., and Putti,
T. (2008). Automatic Breast Cancer Grading of
Histopathological Images. In International Confer-
ence of the IEEE Engineering in Medicine and Biol-
ogy Society, pages 3052–3055.
Detre, S., Saccani Jotti, G., and Dowsett, M. (1995). A
”quickscore” method for immunohistochemical semi-
quantitation: validation for oestrogen receptor in
breast carcinomas. Journal of Clinical Pathology,
48(9):876–878.
Doyle, S., Agner, S., Madabhushi, A., Feldman, M., and
Tomaszewski, J. (2008). Automated grading of breast
cancer histopathology using spectral clustering with
textural and architectural image features. In IEEE In-
ternational Symposium on Biomedical Imaging: From
Nano to Macro, pages 496–499. IEEE.
Kononen, J., Bubendorf, L., Kallionimeni, A., Brlund, M.,
Schraml, P., Leighton, S., Torhorst, J., Mihatsch, M.,
Sauter, G., and Kallionimeni, O. (1998). Tissue mi-
croarrays for high-throughput molecular profiling of
tumor specimens. Nature Medicine, 4(7):844–847.
Kostopoulos, S., Cavouras, D., Daskalakis, A., Bougioukos,
P., Georgiadis, P., Kagadis, G., Kalatzis, I., Rava-
zoula, P., and Nikiforidis, G. (2007). Colour-Texture
based image analysis method for assessing the Hor-
mone Receptors status in Breast tissue sections. In
International Conference of the IEEE Engineering
in Medicine and Biology Society, pages 4985–4988.
IEEE.
Nabney, I. (2002). NETLAB: algorithms for pattern recog-
nition. Springer-Verlag, New York.
Petushi, S., Garcia, F., Haber, M., Katsinis, C., and Tozeren,
A. (2006). Large-scale computations on histology im-
ages reveal grade-differentiating parameters for breast
cancer. BMC Medical Imaging, 6:14.
Zhang, J., Petushi, S., Regli, W., Garcia, F., and Breen, D.
(2008). A study of shape distributions for estimating
histologic grade. In International Conference of the
IEEE Engineering in Medicine and Biology Society,
pages 1200–1205.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
248
