LOCMAX SIFT

Non-Statistical Dimension Reduction on Invariant Descriptors

Dávid Losteiner

Péter Pázmány Catholic University, H-1083 Budapest, Práter u. 50/a, Hungary

László Havasi and Tamás Szirányi

Distributed Event Analysis Research Group, Hungarian Academy of Sciences, H-1111 Budapest, Kende u. 13-17. Hungary

Keywords: SIFT, Dimension reduction, DTW, Image descriptors.

Abstract: The descriptors used for image indexing - e.g. Scale Invariant Feature Transform (SIFT) - are generally

parameterized in very high dimensional spaces which guarantee the invariance on different light conditions,

orientation and scale. The number of dimensions limit the performance of search techniques in terms of

computational speed. That is why dimension reduction of descriptors is playing an important role in real life

applications. In the paper we present a modified version of the most popular algorithm, SIFT. The

motivation was to speed up searching on large feature databases in video surveillance systems. Our method

is based on the standard SIFT algorithm using a structural property: the local maxima of these high

dimensional descriptors. The weighted local positions will be aligned with a dynamic programming

algorithm (DTW) and its error is calculated as a new kind of measure between descriptors. In our approach

we do not use a training set, pre-computed statistics or any parameters when finding the matches, which is

very important for an online video indexing application.

1 INTRODUCTION

Image descriptors are basic features in video

processing applications. There are several real-life

areas such as object recognition; video indexing or

searching in image databases where stable image

features play the most important role (Lowe, 1999).

An early concept was only to find specific keypoints

of digital images (Mikolajczyk and Schmid, 2005)

but nowadays we use much more stable features, so

called descriptors, to exploit a considerable amount

of usable information from an image area.

Building a huge database from video frames is

very time consuming if the dimensionality is high. In

our case – as one of the most preferred ways – the

Scale Invariant Feature Transformation (SIFT)

produces a very long and accordingly responsible

vector about a point and its environment. However,

when the matching of these points is based on a

simple method - e.g. an Euclidian distance on

vectors of the same size -, in case of large amount of

data some serious problems could emerge. The cost

of these can be reduced using e.g. PCA to decrease

the vectors’ dimension but this means some extra

pre-computation steps on a given patch set to get the

eigenspace (Ke and Sukthankar, 2004). However, it

results in a significantly lower dimension compared

to standard 128 element vectors, but it is also needed

to be executed offline.

We discuss here some other ways to decrease

dimensions and to make the computing effort of

searching much lower.

The motivation was to find an alternative for the

conventional matching method which is required to

determine the two smallest distances in the dataset.

For a small number of descriptors it works perfectly,

but in larger databases this quotient leads to possible

false matches.

We will present lower dimension descriptors

which are based on the structural properties of the

SIFT descriptors to narrow the space where we have

to search. On the other hand, decreasing the

descriptors’ dimension results in the loss of a part of

information so the error distance computation needs

to focus on really relevant SIFT properties. Another

benefit to other solutions that locmax (local

192

Losteiner D., Havasi L. and Szirányi T. (2009).

LOCMAX SIFT - Non-Statistical Dimension Reduction on Invariant Descriptors .

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 192-195

DOI: 10.5220/0001799401920195

 SciTePress

maximas on SIFT descriptor) does not need pre-

computed statistics (Hua et al, 2007) or any training

dataset (Mikolajczyk and Schmid, 2001).

The paper is organized as follows. In Section 2

we introduce the locmax SIFT features. Then we

propose a new error-distance on locmax SIFT

parameters by using the DTW method and applying

its effort for matching the most significant peaks.

Finally, we demonstrate the efficiency of the

proposed metric and the new methodology.

2 PROPOSED DESCRIPTOR

The idea came from the analysis of correctly

matched SIFT descriptor vectors (Lowe 2004). An

important property of these is the corresponding

local peaks are close on descriptor vectors. All the

descriptors never fit each other completely; they are

just very similar to each other. For example, the

rotation of an object can produce some changes in

the feature vector because of the discrete

transformation but it will not really act on local

maxima peaks (hereafter called locmax). We will

show that slight changes caused by different maxima

do not affect significantly the matching processes.

In our attempts, when using the local maxima,

only 3 neighboring values are checked so the 128

long descriptor may contain no more than 128/3=42

locmax positions. In practice this number spans from

15 to 32 considering our experiments where on

10000 SIFT descriptor we get around 20 as average

number of peaks (with near Gaussian distribution).

This simple restriction decreases the vector

dimension significantly

Here we exploit the fact that the locmax statistics

of the same point in different instances can be

changed but its structure can be related to the other

in the modified version as well. Our experiments

show that these locmaxes are stable enough for

matching, and reduce the dimension of the search.

The other motivation was to work around the above

mentioned standard distance calculation and thereby

to use a threshold value at finding pairs.

2.1 Extraction of LocMax Values

The only thing to do with the standard SIFT

descriptors is to extract locmax positions and values.

The extraction of locmaxes based on a simple search

of local maxima among the neighboring descriptor

values. The simplest case is to use a 3 element wide

window for this step.

As we mentioned above, the locmax descriptors

yield much lower dimension vector. From our

perspective the important information are the

indexes and the values of these extremes.

As we will show, for the calculation of distances

between two locmax vectors we used the retrieved

positions. This distance will be low in case of

similar maxima positions, but the source SIFT

descriptors also include low maxima values. If these

low values are just slightly higher than its

neighboring ones then there will be also local

maxima.

For this reason we use the values as weighting

factors at a distance calculation, and the matching

does not depend on them directly. The most

dominant values of the descriptor vector take the

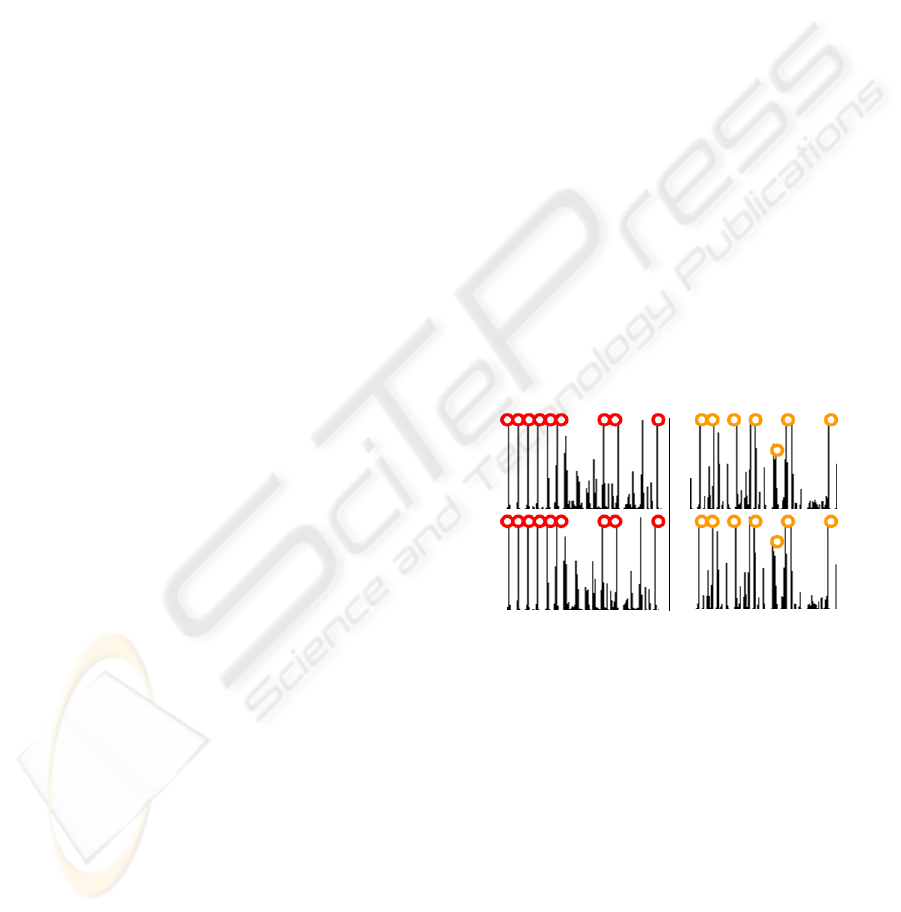
same positions (Figure 1) hence if the difference is

low between those positions the current weighted

distance will be also low. In case of a high

difference the current position match is just a

‘casual’ correspondence and we should compensate

the distance among weights as described later. In the

optimal case it means that only really similar

locmaxes have a low distance from their

counterparts.

For the further detailed description of the

weighted distance calculation see Section 2.2.

Figure 1: Standard way for pairing descriptors. Local

maximas take the same positions.

2.2 Comparison of LocMax

Descriptors

The SIFT values are to be normalized according to

the global maxima in the range of [0, 1] for each

descriptor. This is necessary because the weighting

function only uses the structural similarity among

the descriptors.

Using only the position indexes is not enough to

get the correct distance because it is not just the

position but also the weight that is determining the

structural similarity (2). Because of the possible

difference between two locmax vector lengths, we

used the DTW (Dynamic Time Warping) algorithm

LOCMAX SIFT - Non-Statistical Dimension Reduction on Invariant Descriptors

193

(Myers and Rabiner, 1981) to compare the positions

and to get the error distance. The algorithm is

successfully used in signal processing tasks such as

speech recognition and text processing.

Before running the DTW we have to calculate

the distance between position vectors, which

generates a distance matrix D :

() ( )

(, ) () ( )

wi w j

Di j p i p j e

−

=− +

(1)

where p

and p

are position vectors, w

and w

are

normalized values from SIFT. Next, using the

normalized weights, we will correct the matrix and

increase the distance if necessary:

(, ) (, ) (1 () ( ))

ij Dij wi w j=⋅+−

(2)

Using this compensation, the DTW algorithm is

now ready to compute distances on weighted D

distance matrix. If the weights are different the

above mentioned function will enhance the possibly

low distance and in case of equivalent values it has

no effect really (Figure 2). The DTW follows the

classical algorithm of (Myers and Rabiner, 1981);

just the format of the input has changed, instead of

using vectors we used the compensated D matrix.

This results the distance matrix D. This method was

used to compare two locmax descriptors and get our

own metric on positions and values.

()

TW D

dist

(3)

where k is the number of DTW steps.

Figure 2: Example for weighted matrix created from

correct locmax match.

To get some extra speed up we use a default high

value if the positions are unlikely far from each

other so the DTW never will run on that area. Using

this locmax distance no more effort is needed to

search after the best and second best Euclidian

distance (Lowe, 2004) and we can easily rank the

descriptors.

The mentioned algorithm ends with a simple

nearest neighbor search where there is no need for a

threshold value. The distances tell us a measure of

similarity between SIFT vector structures. The

paired locmaxes were taken from a ground truth set,

of course. In the paper, test images and homography

data are from the data set used for performance

evaluation of the descriptors (Mikolajczyk and

Schmid, 2005), however, our goal is not a

comparative study among different descriptors

(Figure 3).

The complexity of this distance calculation

requires more computation (Table 1). To reduce the

computational steps, we used the above suggested

default high value on positions which are too far

from the main diagonal on D. This default value can

be easily set to a fairly high number. This way the

computation is reduced to a given band along the

diagonal.

The DTW algorithm runs twice on the weighted

distance matrix D: first it determines the distance

field, then finds the minimum route on it that will

also produce the k number of steps (3). Because of

setting up the far positions, the DTW does not need

to deal with uninteresting parts of D distance matrix.

Instead of working on an N-by-M matrix we should

just use the relevant information which cannot be

determined directly, because it depends on position

distances and the limit of allowed distance L

on D.

Table 1: Computation costs of locmax distances.

3 EXPERIMENTAL RESULTS

We have shown a novel distance calculus for SIFT

matching for achieving more effective indexing and

retrieval solutions with reduced dimensionality. We

compared the standard SIFT, the descriptors reduced

with PCA algorithm (Joliffe, 1986) using 20

dimension descriptors, and the locmax approach.

The results in Table 2 show the precision as a

percentage value in case of adding two and more

images and in brackets the total number of found

descriptor pairs. The correctness of the matching

was also tested geometrically with the given ground

truth homographies (Mikolajczyk and Schmid,

2005). The higher precision value means the higher

rate of correct matches. These values mean how the

percentage of correctly founded matches change to

the reference descriptor set (number in brackets) if

we add new elements to the database. Our primary

goal was not to overcome any previous SIFT

Calculating D matrix

(

)

()

NM L Dij⋅− <

DTW

()

NM L Dij k

⋅

−< +

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

194

Table 2: Number of matches on SIFT and locmax-SIFT descriptors.

Graffiti +Boat +Bark + Bikes

#descr. on image 900+1083 +844 +1255 +597

SIFT 94% (402) 87% (394) 87% (394) 83% (386)

SIFT (PCA) 81% (555) 76% (589) 60% (760) 57% (769)

locmax 89% (411) 83% (415) 78% (426) 74% (432)

Figure 3: Samples from used image dataset [4] (Graffiti, Boat, Bark, Bikes).

method, but to create a lower dimensional descriptor

which is stable enough.

The most of false matches came from textured

regions because the locmax vectors contain only the

most significant parts of SIFT features (e.g. Bark,

see Figure 3). Certainly the dimension reduction

causes loss of information, thus there will be similar

local maxima positions from such areas. Another

problem is the uncertainty of good and false

matches.

In summary, higher precision leads to better

detection rates for object retrieval (Schügerl et al,

2007). The proposed method can improve the

precision rate in the reduced dimensions.

4 CONCLUSIONS

This paper introduced a new type of error-distance

calculation on SIFT descriptors with decreased

dimension. The method uses only a dynamic set of

local maxima of standard feature vectors, and after

calculating a weighted position distance we use the

DTW algorithm for comparing locmax features, and

get a novel metric on descriptors. This makes

possible the unsupervised (non-linear) dimension

reduction which is the key step to construct an

effective search tree in the future.

In future works we will focus on perfecting the

weight function to improve the matching scores,

according to other structural properties of SIFT

descriptors. Another plan is to integrate it in a lower

dimensional tree structure.

REFERENCES

Brown, M. and Lowe, D. G., 2003. Recognizing

Panorama, Proceedings of Ninth IEEE International

Conference on Computer Vision Vol.2 pp. 1218- 1225

Hua, G., Brown, M., Winder, S., 2007. Discriminant

Embedding for Local Image Descriptors, IEEE

International Conference on Computer Vision, Rio de

Janeiro, Brazil, pp. 1-8.

Joliffe, I.T., 1986. Principal Component Analysis.

Springer-Verlag.

Ke, Y., and Sukthankar, R., 2004. PCA-SIFT: A More

Distinctive Representation for Local Image

Descriptors. CVPR 2004. Proceedings of the 2004

IEEE Computer Society Conference on, Vol.2 , pp.

506-513.

Lowe, D., 1999. Object recognition from local scale-

invariant features. In Proceedings of International

Conference on Computer Vision, pp. 1150–1157.

Lowe, D., 2004. Distinctive image features from scale-

invariant keypoints. International Journal of

Computer Vision. pp. 91-110.

Mikolajczyk, K. and Schmid, C., 2001. Indexing based on

scale invariant interest points. In Proceedings of

International Conference on Computer Vision, pp.

525–531.

Mikolajczyk, K. and Schmid, C., 2005. A performance

evaluation of local descriptors. IEEE Transaction on

Pattern Analysis and Machine Intelligence, pp.

27(10):1615–1630.

Myers, C. S. and Rabiner, L. R. 1981. A comparative

study of several dynamic time-warping algorithms for

connected word recognition. The Bell System

Technical Journal, pp. 60(7):1389-1409.

Schügerl, P., Sorschag, R., Bailer, W., Thallinger, G.,

,2007. Object Re-detection Using SIFT and MPEG-7

Color Descriptors, Multimedia Content Analysis and

Mining, Springer-Verlag, pp. 305-314.

LOCMAX SIFT - Non-Statistical Dimension Reduction on Invariant Descriptors

195