
EIGENVECTOR ANALYSIS FOR OPTIMAL FILTERING
UNDER DIFFERENT LIGHT SOURCES
Juha Lehtonen, Jussi Parkkinen
Department of Computer Science and Statistics, University of Joensuu, P.O. Box 111, FI-80101 Joensuu, Finland
Timo Jaaskelainen
Department of Physics and Mathematics, University of Joensuu, P.O. Box 111, FI-80101 Joensuu, Finland
Alexei Kamshilin
Department of Physics, University of Kuopio, P.O. Box 1627, FI-70211 Kuopio, Finland
Keywords: Color spectrum, Eigenvector, Filtering, Illuminant, Sampling interval.
Abstract: Eigenvectors from Standard Object Colour Spectra (SOCS) set were used with several other spectra sets to
find the optimal sampling intervals for optimal number of eigenvectors. The sampling intervals were
calculated for each eigenvector separately. The analysis was applied not only for different sets of reflectance
spectra, but also for spectra sets under different real light sources and standard illuminations. It is shown
that 20 nm sampling interval for eigenvectors from SOCS set can be used for reflectance data and data
under such light sources which spectrum is smooth. However, data under peaky real fluorescent light
sources and standard F-illuminant require accurate 5 nm or even narrower sampling interval for the first few
eigenvectors, but can be wider with some of the others. These eigenvectors from SOCS set are shown to be
applicable for the other data sets. The results give guidelines for the required accuracy of eigenvectors under
different light sources that can be considered e.g. in eigenvector-based filter design.
1 INTRODUCTION
Color is usually represented with three components,
such as with RGB color coordinate system. In many
cases, this is not enough. Trichromatic
representations of color are depended on the used
device and illumination, and those are affected by
metameric issues (Morovic, 2002). These problems
can be avoided with accurate spectral representation
of color. The use of spectral color is becoming more
and more popular. Spectra are needed for example in
telemedicine (Nishibori, 2002), e-commerce, digital
art museums (Martinez et al., 2002), art restoration,
quality control (Hyvärinen et al., 1999) etc.
However, accurate spectral color measurement
devices are expensive and measurement may be
difficult in a noisy environment. Accurate non-
compressed spectral data require also a lot of
memory, which will cause problems in using, storing
and transferring tasks (Hauta-Kasari et al., 2006).
Spectral dimensionality has been widely studied.
This consists of finding the required sampling
interval of color spectra (Buchsbaum & Gottschalk,
1984; Maloney, 1986; Bonnardel & Maloney, 2000;
Lehtonen et al., 2006), and transforming the spectra
to another lower dimensional space (Parkkinen et al.,
1989; Hyvärinen et al., 2001; Schettini, 1994; Early
& Nadal, 2004). One widely used method is
Principal Component Analysis (PCA) (Parkkinen et
al., 1989), where the data dimensionality is reduced
with the eigenvectors of the data. Several
applications based on PCA, such as non-negative
filters for imaging have been developed (Piché,
2002). By Hauta-Kasari et al., (1998), the
eigenvector-based non-negative filters make it
possible to produce the inner-product set in
hardware level. From the measured data, accurate
spectral information can be computed.
However, to the authors’ knowledge, optimal
number of eigenvectors under different illuminants
95
Lehtonen J., Parkkinen J., Jaaskelainen T. and Kamshilin A. (2009).
EIGENVECTOR ANALYSIS FOR OPTIMAL FILTERING UNDER DIFFERENT LIGHT SOURCES.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 95-100
DOI: 10.5220/0001798700950100
Copyright
c
SciTePress

combined with the required spectral accuracy of the
eigenvectors has not been studied. Here we will
create such sets of eigenvectors under different light
sources that can be used for several other color data
sets. This includes also a study of required spectral
accuracy of eigenvectors. The results can be used
e.g. in filter design to create optimal number of non-
negative color filters for different illuminants, which
can be used generally for accurate color
measurements (Piché, 2002; Hauta-Kasari et al.,
1998).
2 THEORY
A widely used method for reducing the dimensions
of color spectra is Principal Component Analysis
(PCA) (Parkkinen et al., 1989). Let C be a
correlation matrix
.
1
1
∑
=
=
N
i
T
ii
SS
N
C
(1)
Here S
i
is ith spectrum of a spectra set S and N is the
number of spectra. The h first eigenvectors of the
spectra set ordered by the largest eigenvalues can be
calculated. The inner-product set P is then formed
with equation
()
,,...,,
21
SP
T
h
τττ
=
(2)
where
()
h
τ
τ
τ
,...,,
21
and T denotes the eigenvectors
and matrix transpose, respectively. The data can be
reconstructed back to spectra with the linear
combination of
()
h
τ
τ
τ
,...,,
21
and inner-product set
P.
If spectra data set is well defined, one might use
the eigenvectors calculated from it to reduce the
dimensionality of any other spectra set. In this study,
we try to use the eigenvectors of a data set with
different other data sets and optimize the sampling
intervals of the eigenvectors. Each eigenvector was
sampled to several sampling intervals
straightforward and then interpolated back with
Lagrange interpolation used by Fairman (1985)
before reconstruction of spectra. Such number of
eigenvectors and sampling intervals were chosen
that the reconstructed spectra have good quality. For
this, several quality and error measurements were
done defined in chapter 4. This analysis was studied
with the reflectance spectra and also with spectra
under different real light sources and standard
illuminants. However, since the eigenvectors are
sampled and interpolated, those are not orthogonal
after conversion, and calculating with PCA is not
straightforward. A pseudoinverse matrix is required
to fix the orthogonality, and the reproduction can be
calculated with
() ()
,
1
SS
T
rr
T
rrr
ττττ
−
⎥
⎦
⎤
⎢
⎣
⎡
=
(3)
where
r
τ
is the sampled and interpolated
eigenvectors
),,...,,(
21
r
h
rr
τττ
and S
r
is the
reconstructed spectra set. In this study, a term
eigenvector index is used to denote the eigenvector
index number 1...h, where the eigenvectors are
ordered in descending order by the eigenvalues.
3 DATA SETS
Ten different spectra sets (University of Joensuu,
2008; Japanese Standards Association, 1998;
Kohonen et al., 2006; Funt & Lewis, 2000;
Farnsworth, 1957; Jaaskelainen et al., 1994;
Pantone, 2008) were used, listed in Table 1. The
spectra originally measured with wider sampling
interval than 1 nm were interpolated with Lagrange
method shown by Fairman (1985) to 1 nm data and
treated as original data. According to Lehtonen et al.
(2006) and Sándor et al. (2005) this can be done,
since interpolated reflectance spectra are very near
to spectra measured with 1 nm. Spectral values
outside 400...700 nm range were eliminated.
Table 1: Data sets.
Data set Nr.
of
spectra
Original
wavelength
area [nm]
Original
sampling
[nm]
Dupont
1
120 400...700 4
FM100
2
85 400...700 5
Wood
3
1,056 390...850 5
Lumber 272 380...2700 1
Munsell Glossy
4
1,600 380...780 1
Munsell Matte
4
1,269 280...800 1
Object Spectral Reflect-
ance Database (OSRD)
1
170 400...700 4
Pantone
5
922 380...780 1
Printed Colors 2,240 380...780 1
Standard Object Colour
Spectra (SOCS)
6
49,392 400...700 5, 10
1
Funt & Lewis, 2000.
2
Farnsworth, 1957.
3
Jaaskelainen et al.,
1994.
4
University of Joensuu, 2008.
5
Pantone, 2008.
6
Japanese
Standards Association, 1998.
At first, eigenvectors from different data sets
were tried to be used separately for other data sets.
According to tests, suitable eigenvectors can be
calculated from both Munsell sets (University of
Joensuu, 2008), from Pantone set (Pantone, 2008)
and from Standard Object Colour Spectra (SOCS)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
96
set (Japanese Standards Association, 1998). The
spectra of the Munsell sets and Pantone set vary a
lot. For example Munsell set describes the colors of
CIE L*a*b* coordination well, and therefore the
eigenvectors are formed for the whole coordination.
However, both Munsell sets and also Pantone set
had problems with Wood data set (Jaaskelainen et
al., 1994), requiring near 20 eigenvectors for good
result, but this problem was not an issue in any set
with eigenvectors of SOCS set. SOCS data set
includes 49,392 spectra from photographic
materials, printed colors, paints, textiles, human
skin, flowers and leaves. This is a wide collection of
color spectra and therefore, the eigenvectors of this
set can represent several types of data well.
The sampled and interpolated eigenvectors from
SOCS data set were calculated. These eigenvectors
were used as a base for calculating the inner-
products of other spectra sets and for reconstruction.
The required number of eigenvectors and the needed
sampling interval of eigenvectors were found with
calculating the quality of reconstructed spectra. The
number of eigenvectors was chosen as the smallest
possible. This procedure was also experimented with
the reflectance data, data under four different real
light sources and five standard illuminants A, D65,
F2, F8 and F11. Spectra of the real light sources are
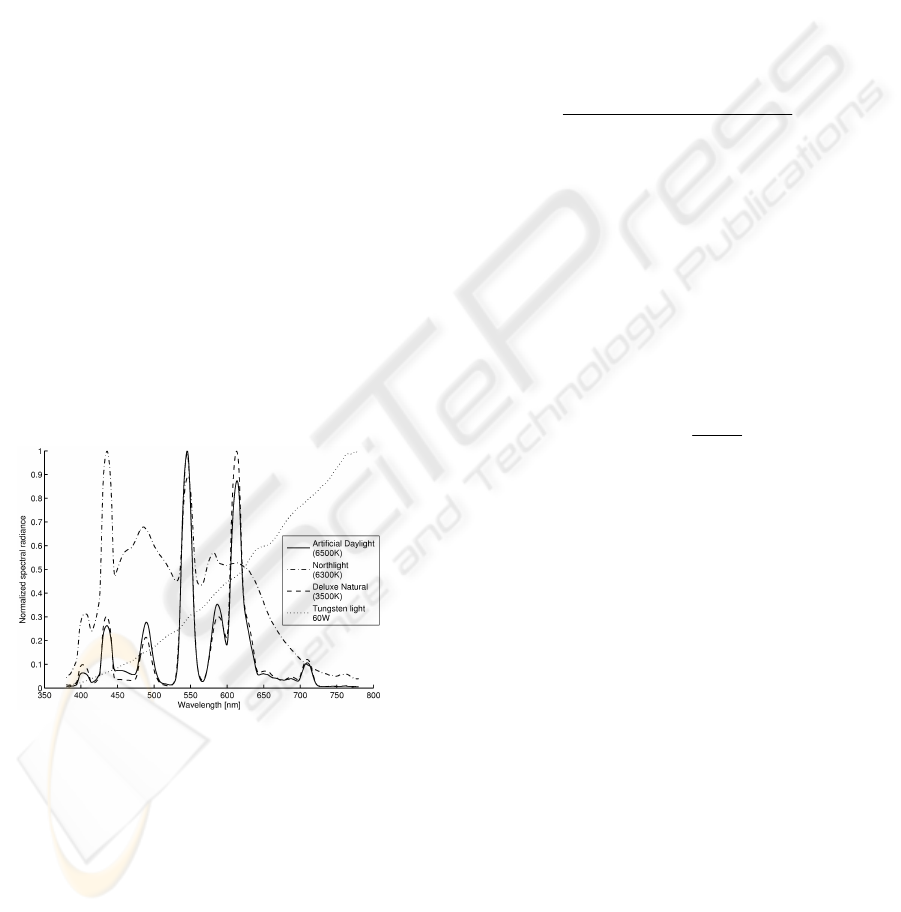
shown in Figure 1. In these cases, also the SOCS
data was converted under the light source or
illuminant before PCA calculations.
Figure 1: Spectra of the real light sources.
4 QUALITY AND ERROR
MEASURES
Two quality measures and one error measure were
used to define the quality of reconstructed spectra.
The error measure is ΔE, which measures the visual
color difference in CIE L*a*b* color coordination as
()
,***
2/1
222
baLE Δ+Δ+Δ=Δ
(4)
where ΔL*, Δa* and Δb* are the component
differences between the original and reconstructed
color values in CIE L*a*b* color space. According
to Ohta and Robertson (2005), ΔE = ~1.0 is usually
discriminable. Parkkinen et al. (1989) use color limit
of average ΔE < 0.5. Equal-energy spectrum was
used as illuminant with calculating the tristimulus
values.
Goodness-of-Fit Coefficient (GFC) (Hernández-
Andrés et al., 2001) is a correlation based quality
measure between two spectra, measuring the
similarity of two spectra. It is defined as
() ()
,
2/1
1
2
2/1
1
2
1
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
∑∑
∑
==
=
n
k
r
k
n
k
o
k
n
k
r
k
o
k
GFC
ss
ss
ε
(5)
where n is number of channels in spectrum. Terms
o
k
s and
r
k
s are the wavelength channel values of
original and reconstructed spectra, respectively.
According to Hernándes-Andrés et al. (2001), good
limit for this quality measure is 0.999 and accurate
limit 0.995.
Peak Signal-to-Noise Ratio PSNR is widely used
quality measure in image compression, defined as
,
ˆ
log10
2
10
MSE
PSNR
s
ε
ε
=
(6)
where ε
MSE
is Mean Square Error and s
ˆ
is the
theoretical maximum of a channel value in
spectrum.
Based on Parkkinen et al. (1989), Ohta &
Robertson (2005) and Hernandéz-Andrés et al.
(2001), the quality and error limits were chosen as
average ΔE < 0.5, average GFC > 0.999 and average
PSNR > 40 dB. To obtain accurate results, all of
these limits must be satisfied in spectra
reconstruction. Also, when selecting a suitable
number of eigenvectors and sampling interval, it is
required that all narrower sampling intervals and
higher number of PCA components must satisfy
with the limits.
The quality and error measures and the selected
limits were compared with each other with the data
sets under Artificial Daylight source, illuminant F11
and illuminant D65. With each light source, the GFC
limit 0.999 and PSNR limit 40 dB correspond well
with each other, and both accept and reject same
sampling intervals. Similar result is found with ΔE
compared to GFC or PSNR for the data under
Artificial Daylight source. However, the ΔE limit is
EIGENVECTOR ANALYSIS FOR OPTIMAL FILTERING UNDER DIFFERENT LIGHT SOURCES
97
more unforgiving with data under F11 illuminant,
accepting 1...4 nm sampling intervals, whereas GFC
and PSNR accept only 1...2 nm sampling intervals.
Also, ΔE error does not always correspond with the
sampling interval. With some cases the average
visual error is smaller but the average spectral error
is higher with wide sampling interval than with
narrow sampling interval. Some small variations can
also be found with the quality measures, e.g. with
F11 illuminant GFC and PSNR values are better
with 5 nm sampling interval than 4 nm interval. For
these reasons, also all more accurate sampling
intervals than the selected one must satisfy with the
limits.
5 PARAMETER SELECTIONS
The results of the required number of PCA
components and sampling intervals of different
eigenvectors with different reflectance data sets and
data sets under Artificial Daylight source are shown
in Table 2. The eigenvectors of SOCS data is used.
For all reflectance data sets, 20 nm interval is
enough for the eigenvectors. The required number of
eigenvectors varies between 6...11, depending on the
variety of colors in data set and data set difference
from SOCS set. However, majority of the data sets
can be represented with eight eigenvectors. For data
under Artificial Daylight source, 4...6 nm interval is
needed for the first eigenvector, but can be wider
with most of the data sets with higher index
eigenvectors. Also, 4...8 eigenvectors are required
depending on the data set.
The overall results of the reflectance data sets
and data sets under different light sources are shown
in Table 3. Here, the total averages of different
quality and error measures were used, weighted
equally between different sets. With reflectance data
and data under smooth light sources the required
sampling interval for SOCS eigenvectors is 20 nm.
In average for all data sets, ten PCA components are
required with the reflectance data and data under
D65 illuminant. Eight PCA components are enough
for data under illuminant A and Tungsten light
source. The required sampling interval for the first
few eigenvectors of SOCS are 4...5 nm with data
sets under real fluorescent light sources, but interval
can be wider for higher index eigenvectors.
Depending on the light source, 5...8 PCA
components are required. For data under F-
illuminants, 1...3 nm interval is needed, but with F2
and F11, the interval can be wider for higher index
eigenvectors. In average for all data sets, 5...10 PCA
components are required depending on the light
source. It was also found that 0...2 less eigenvectors
from SOCS set are enough for the use with SOCS
spectra set alone, compared to use with other data
sets. Some average and bad examples of spectra
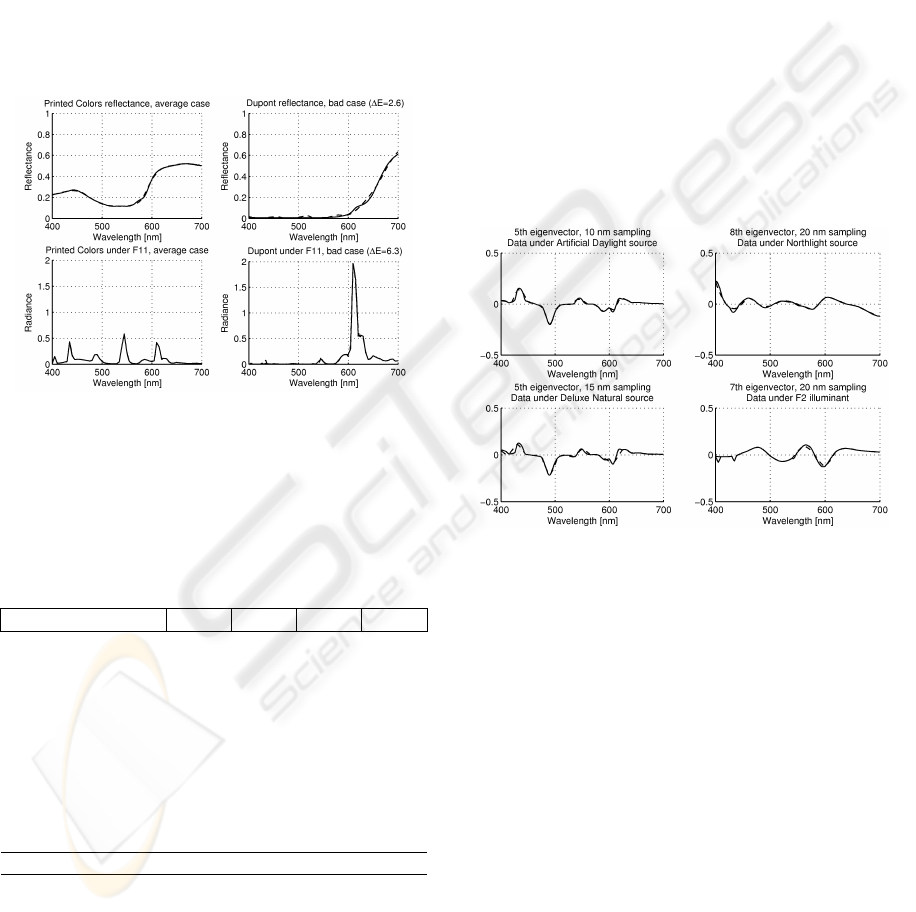
reconstruction are shown in Figure 2 when the
eigenvectors of SOCS data with sampling intervals
shown in Table 3 are used.
Table 2: Required sampling intervals of eigenvectors of
SOCS data when used with different data sets.
Reflectance Eigenvector index
data set 1 2 3 4 5 6 7 8 9 10 11
Dupont 20 20 20 20 20 20 20 20 20 - -
FM100 20 20 20 20 20 20 20 20 - - -
Forest 20 20 20 20 20 20 20 20 20 20 20
Lumber 20 20 20 20 20 20 - - - - -
Munsell G. 20 20 20 20 20 20 20 20 - - -
Munsell M. 20 20 20 20 20 20 20 20 - - -
OSRD 20 20 20 20 20 20 20 20 20 20 -
Pantone 20 20 20 20 20 20 20 20 - - -
Printed Col. 20 20 20 20 20 20 - - - - -
SOCS 20 20 20 20 20 20 20 20 - - -
Data under Eigenvector index
Artif. Dayl. 1 2 3 4 5 6 7 8
Dupont 5 4 5 11 9 11 20 10
FM100 4 7 6 11 15 - - -
Forest 5 9 9 20 13 10 8 -
Lumber 6 9 8 6 - - - -
Munsell G. 5 7 6 5 15 - - -
Munsell M. 5 7 5 11 15 - - -
OSRD 5 5 5 15 6 13 10 20
Pantone 4 7 6 9 11 14 - -
Printed Col. 5 5 9 13 14 - - -
SOCS 5 7 9 10 11 - - -
Table 3: Required average sampling intervals of
eigenvectors of SOCS data when used with all data sets
and under different light sources.
All data sets Eigenvector index
Light source 1 2 3 4 5 6 7 8 9 10
Reflectance 20 20 20 20 20 20 20 20 20 20
Artif. Daylight 5 7 5 5 10 - - - - -
N
orthlight 5 12 12 13 8 6 8 20 - -
Deluxe Natural 4 4 5 9 15 - - - - -
Tungsten lamp 20 20 20 20 20 20 20 20 - -
A 20 20 20 20 20 20 20 20 - -
D65 20 20 20 20 20 20 20 20 20 20
F2 1 3 5 9 13 6 20 - - -
F8 2 1 3 3 1 2 3 1 3 -
F11 2 6 3 7 6 3 7 7 - -
The spectra from each group and each light
source were divided in four groups based on the
resulted average quality and error calculations. The
average relative numbers of spectra in different error
groups for different light sources are shown in Table
4, when quality and error measures are weighted
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
98
equally between the test sets. SOCS data was not
included in the test sets, it was only used to form the
eigenvectors. In general, over 90% of the spectra
sets are located in highest quality groups a) and b).
Only exceptions are found with Artificial Daylight
source and F11 illuminant, where the relative
number is 80%. Only about 1% of the spectra give
high error, see group d). A small exception is found
with F11 illuminant, where the number of bad
spectra is 3.8%. However, most of these spectra are
selected as bad only because PSNR values very near
30 dB is achieved, but not quite. If this quality limit
was changed to PSNR = 28 dB, the relative number
of bad spectra would be 1.6%.
Figure 2: Some average and bad examples of spectrum
reconstruction. Original spectrum is shown as solid line
and reconstructed one as dashed line.
Table 4: Relative number of spectra distributed with
quality and error measures when eigenvectors of SOCS
data with sampling interval listed in Table 3 is used.
All data sets,
not SOCS
Light source a) b) c) d)
Reflectance 83.7% 14.8% 1.5% 0.0%
Artificial Daylight 40.1% 42.8% 15.4% 1.7%
N
orthlight 57.4% 34.9% 6.8% 0.9%
Deluxe Natural 56.5% 35.7% 6.7% 1.2%
Tungsten lamp 68.9% 20.9% 9.0% 1.2%
A 74.3% 21.5% 3.8% 0.4%
D65 64.4% 33.8% 1.8% 0.0%
F2 56.4% 34.1% 8.3% 1.2%
F8 62.8% 26.4% 9.5% 1.3%
F11 30.5% 47.7% 18.0% 3.8%
Average 59.5% 31.3% 8.1% 1.2%
a) (ΔE < 0.5) AND (GFC > 0.999) AND (PSNR > 40dB)
b) (0.5 ≤
ΔE < 1.0) AND (0.995 < GFC ≤ 0.999) AND
(34dB < PSNR ≤ 40dB)
c) (1.0 ≤
ΔE < 3.0) OR (0.990 < GFC ≤ 0.995) OR
(30dB < PSNR ≤ 34dB)
d) (
ΔE ≥ 3.0) OR (GFC ≤ 0.990) OR (PSNR ≤ 30dB)
6 CONCLUSIONS
For reflectance data and data under those light
sources, which spectrum is smooth, the eigenvectors
are also smooth, and wide 20 nm sampling interval
is enough. For data under real fluorescent light
sources, the peaky dominating shape caused by the
light source is located in the eigenvectors, and the
required sampling interval is accurate in lower
indexes, near 5 nm, but can be a bit wider with some
higher indexes, near 10 nm. F-illuminants require
more accurate sampling interval compared to real
fluorescent light sources, between 1...7 nm
depending on the eigenvector index. Since the
higher index inner-products do not contain much
overall information, the corresponding eigenvectors
can have some more errors than lower index
eigenvectors. Few examples of errorous
eigenvectors are shown in Figure 3.
Figure 3: Some bad examples of eigenvectors with wide
sampling. Original eigenvector is shown as solid line and
reconstructed one as dashed line.
The data set under a light source, which
spectrum is peaky, require also few less PCA
components compared to reflectance data or data
under a smooth light source. The aggressive shape of
peaky light source limits the spectra more similar to
each other and therefore less PCA components are
required.
The results show also that eigenvectors defined
from large variety of data, such as from SOCS data
set, work very well generally with other data sets.
The required sampling interval of eigenvectors
depends on the eigenvector index and the light
source. All data sets under a light source give similar
sampling intervals, but the required number of
eigenvectors is different with different data sets and
light sources. However, a general required number
of eigenvectors was found for different light sources
EIGENVECTOR ANALYSIS FOR OPTIMAL FILTERING UNDER DIFFERENT LIGHT SOURCES
99

separately, which can be used to generate low errors.
The results can be useful in applications based on
eigenvectors, such as in designing optimal non-
negative filters for different light sources.
REFERENCES
Bonnardel V., and Maloney, L., 2000. Daylight,
biochrome surfaces and human chromatic response in
the Fourier domain, J. Opt. Soc. Am. A 17(4), 677–
686.
Buchsbaum, G., and Gottschalk, A., 1984. Chromacity
coordinates of frequency-limited functions, J. Opt.
Soc. Am. A 1(8), 885–887.
Early, E., and Nadal, M., 2004. Uncertainty analysis for
reflectance colorimetry, Color Res. Appl. 29(3), 205–
216.
Fairman, H., 1985. The calculation of weight factors for
tristimulus integration, Color Res. Appl. 10(4), 199–
203.
Farnsworth, D., 1957. The Farnsworth-Munsell 100-Hue
Test, Munsell Color Company. Baltimore, MD,
revised ed.
Funt, B., and Lewis, B., 2000. Diagonal versus affine
transformations for color correction, J. Opt. Soc. Am.
A 17(11), 2108-2112.
Hauta-Kasari, M., Lehtonen, J., Parkkinen, J., and
Jaaskelainen, T., 2006. Image Format for Spectral
Image Browsing, J. Imag. Sci. Tech. 50(6), 572-582.
Hauta-Kasari, M., Wang, W., Toyooka, S., Parkkinen, J.,
and Lenz, R., 1998. Unsupervised Filtering of Munsell
Spectra, Proc. of the Third Asian Conference on
Computer Vision, Vol. I, Hong Kong, 248-255.
Hernández-Andrés, J., Romero, J., and Lee Jr., R., 2001.
Colorimetric and spectroradiometric characteristics of
narrow-field-of-view clear skylight in Granada, Spain,
J. Opt. Soc. Am. A 18(2), 412–420.
Hyvärinen, T., Herrala, E., and Dall'Ava, A., 1999. Direct
sight imaging spectrograph: A unique add-on
component brings spectral imaging to industrial
applications, Proc. SPIE 3740, 468-471.
Hyvärinen, A., Karhunen, J., and Oja, E., 2001.
Independent Component Analysis, Wiley.
Jaaskelainen, T., Silvennoinen, R., Hiltunen, J., and
Parkkinen, J., 1994. Classification of the reflectance
spectra of pine, spruce and birch, Appl. Opt. 33, 2356-
2362.
Japanese Standards Association, 1998. Standard object
colour spectra database for colour reproduction
evaluation, TR X 0012.
Kohonen, O., Parkkinen, J., and Jaaskelainen, T., 2006.
Databases for Spectral Color Science, Color Res. Appl.
31(5), 2006, 381-390.
Lehtonen, J., Parkkinen, J., and Jaaskelainen, T., 2006.
Optimal Sampling of Color Spectra, J. Opt. Soc. Am.
A 23(12), 2983–2988.
Maloney, L., 1986. Evaluation of linear models of surface
spectral reflectance with small number of parameters,
J. Opt. Soc. Am. A 3(10), 1673–1683.
Martinez, K., Cupitt, J., Saunders, D., and Pillay, R., 2002.
Ten years of art imaging research, Proc. IEEE 90(1),
28-41.
Morovic, P., 2002. Metamer sets, Ph.D. dissertation,
University of East Anglia.
Nishibori, M., 2002. Problems and solutions in medical
color imaging, Proc. of Second International
Symposium on Multispectral Imaging and High
Accurate Color Reproduction, Chiba, Japan, 2002, 9-
17.
Ohta, N., and Robertson, A., 2005. Colorimetry
Fundamentals and Applications, Wiley.
Pantone, 2008. http://www.pantone.com.
Parkkinen, J., Hallikainen, J., and Jaaskelainen, T., 1989.
Characteristic spectra of Munsell colors, J. Opt. Soc.
Am. A 6(2), 318–322.
Piché, R., 2002. Nonnegative color spectrum analysis
filters from principal component analysis
characteristic spectra, J. Opt. Soc. Am. A 19(10),
1946–1950.
Sándor, N., Ondró, T., and Schanda, J., 2005. Spectral
Interpolation Errors, Color Res. Appl. 30(5), 348-353.
Schettini, R., 1994. Deriving spectral reflectance functions
of computer-simulated object colours, Comput. Graph.
Forum 13(4), 211–217.
University of Joensuu Color Group, 2008. Spectral
Database, http://spectral.joensuu.fi.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
100
