ESTIMATION OF ASYMMETRY IN 3D FACE MODELS

Natalya Dyshkant and Leonid Mestetskiy

Department of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, Moscow, Russia

Keywords:

Facial asymmetry, Quantitative estimation of asymmetry, Surface comparison, Delaunay triangulation, Mini-

mum spanning tree.

Abstract:

This paper proposes a new estimation of facial asymmetry in 3D face models of humans and an algorithm to

compute it. We consider models derived by 3D scanning method. Each model is given as a cloud of points in

3D space and can be considered as a discrete single-valued function of two variables. We present an approach

for constructing a disparity measure between original face model and its reﬂected model. Main stages of pro-

posed algorithm are construction Delaunay triangulations of two models and general Delaunay triangulation,

function interpolation on basis of triangulations localization in each other and comparison of functions on sep-

arate triangles of general triangulation. Further using elementary manipulations of reﬂected model algorithm

searches such position that two models constitute a maximum matching so that the corresponding disparity

measure will be minimal. We carry out computing experiments on database consisting of about 200 face mod-

els. These experiments have indicated that the proposed estimation is stable for different models of one and

the same person.

1 INTRODUCTION

A human face is only approximately bilaterally sym-

metrical with respect to the plane that divides it into

two halves. The aims of this paper are to deﬁne a

degree of such approximation, i.e. degree of facial

asymmetry, and to propose an algorithm to compute

it. A problem of facial asymmetry estimation ap-

pears in such applications as preventionism of child

eyesight anomalies (Knizhnikov, 2005), cosmetology

(facial surgery), psychological and medical (includ-

ing dental) research, etc. Hypothesis checking of

correlation between diagnoses made by ophthalmol-

ogist and measures of facial asymmetry is described

in (Murynin, 2004). Also facial asymmetry can im-

prove results of biometric identiﬁcation (Mitra, 2007)

and facial expression recognition (Teng, 2006) algo-

rithms.

Current 3D imaging technologies allow to re-

ceive three-dimensional models of human faces in

real time.

A model derived by 3D scanning method (see Fig-

ure (1)) is presented as a cloud of point in 3D space

and can be considered as a discrete single-valued

function of two variables z = F(x, y). The z axis rep-

resents front-back displacements of the head. Domain

of each function is a certain discrete set G = {x, y}.

It is proposed to compute sum or mean value of

height difference between points of original and re-

ﬂected 3D models (Liu, 2003) in papers related to fa-

cial asymmetry estimation. This means that values of

two functions (corresponded to original and reﬂected

models) are known in each point of the set G. Ac-

tually models derived by 3D scanning don’t initially

have such property. So a shortage of proposed estima-

tions is that the preprocessing is required. It can cause

loss of observational accuracy. Moreover, it is impos-

sible to use such estimations for computing disparity

measure between two models when we search such

position that models constitute a maximum match-

ing. Main shortages of existed asymmetry estimation

methods are low numericalefﬁciency or loss of source

data accuracy. Therefore the problem of facial asym-

metry estimation is still an urgent problem.

In this paper we propose a new estimation of facial

asymmetry that is computable directly from 3D face

model and an algorithm to calculate it. We present

an approach for constructing a disparity measure be-

tween original face model and its reﬂected model.

Let us remark that functions of original and reﬂected

models are deﬁned on two different discrete sets. We

use elementary manipulations of reﬂected model for

searching such its position that corresponds to mini-

mum of disparity measure. Finally, we deﬁne quanti-

402

Dyshkant N. and Mestetskiy L. (2009).

ESTIMATION OF ASYMMETRY IN 3D FACE MODELS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 402-405

DOI: 10.5220/0001793804020405

 SciTePress

tative asymmetry estimation of 3D model as the min-

imum disparity measure between this model and its

reﬂection.

Figure 1: Receiving of 3D model of human face.

Now we introduce the following concept. Dispar-

ity measure between two models is a spacial volume

between the corresponding surfaces. It is also allowed

to use ”weighted” volume. In this case similarity of

some surface patches will have greater weight than

similarity of others. The mathematical problem has

the following content. Suppose surfaces are given by

functions f(x, y) and g(x, y) on discrete sets G

and

respectively, G

and G

are contained inside a cer-

tain general rectangle R,

f(x, y) and ˆg(x, y) are contin-

uous on R analogs of functions f(x, y) and g(x, y), that

are derived by interpolation: ∀(x, y) ∈ G

f(x, y) =

f(x, y) and ∀(x, y) ∈ G

g(x, y) = ˆg(x, y), function

µ(x, y) deﬁnes weight of surface fragments in accor-

dance with signiﬁcance of their similarity, ∆( f, g) —

disparity measure between functions; then we have:

∆( f, g) =



f(x, y) − ˆg(x, y)



µ(x, y)dxdy.

It is required to design a numerically efﬁcient

method to compute this measure that provide good

accuracy. We can obtain acceptable accuracy using

piecewise-linear approximation of surfaces by trian-

gles of Delaunay triangulations of discrete point sets.

Also, there is a problem of efﬁcient computation of

measure for functions when triangulations are con-

structed on different sets of nodes.

Our method based on constructing of new De-

launay triangulation on union of two discrete sets.

As the union process can be implemented in linear

time (Mestetskiy, 2004) then the total time to com-

pute the proposed measure is comparable with time of

constructing Delaunay triangulation, i.e. O(N logN),

where N — the total amount of points in two sets.

Consequently, the proposed method allows to avoid

quadratic search in surface comparison that deter-

mines its advantage and novelty.

2 3D FACE DATABASE

Three-dimensional models used in this research were

derived by 3D scanner developed in ”Artec Group

company”. The database contains 191 models of 8

different persons. All persons have a neutral facial

expression.

Each model is represented as collection of points

with coordinates (x, y, z) in space. All distances have

a scale of one to one, i.e. correspond to real sizes of

a human face. Amount of points in models changes

from 1000 to 3000, and its mean value is about

1500 − 2000.

Each model has been normalized in such a way

that the end of nose coincides with coordinate ori-

gin, the z axis represents front-back displacements of

a head, the y axis — up-downdisplacements (see Fig-

ure (2)). So we may assume that model is bilaterally

located with respect to the Oyz plane. Note that the

described normalization is assumed only as approxi-

mate.

3 ALGORITHMS

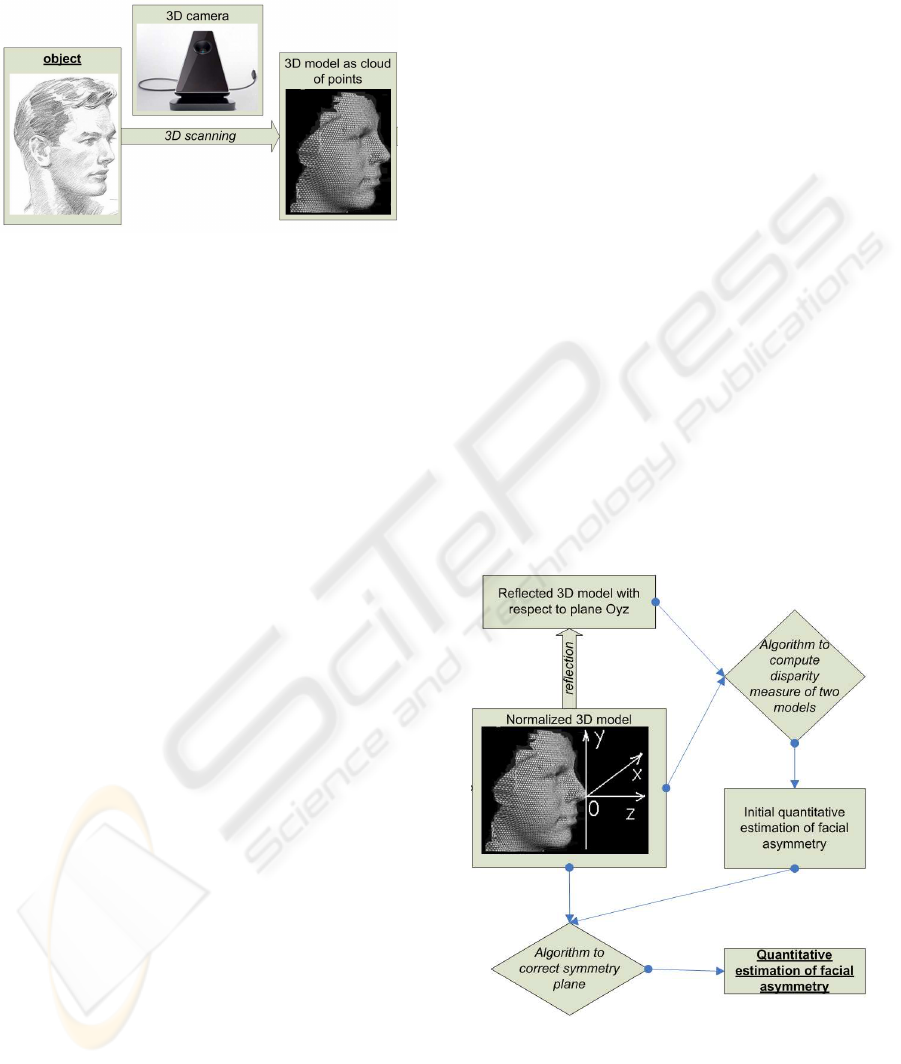
General scheme of presented approach is given on

Figure (2).

Figure 2: General scheme and main stages of presented ap-

proach.

After model normalization in the coordinate sys-

tem we construct its symmetrical reﬂection.

The proposed method of computing a quantitative

estimation of facial asymmetry consists of two stages:

ESTIMATION OF ASYMMETRY IN 3D FACE MODELS

403

1) computing initial estimation as disparity measure

between original and reﬂected models and 2) correc-

tion of symmetry plane of a model.

3.1 Computing Disparity Measure

between Two Models

Main steps of algorithm for computing disparity mea-

sure between two models are:

1. Delaunay triangulation construction of each dis-

crete set;

2. location of each discrete set in triangulation of the

other set;

3. linear interpolation of each function on the other

set using barometrical coordinates;

4. constructing of general triangulation of two dis-

crete sets on basis of merger algorithm;

5. function comparison on particular cells of the gen-

eral triangulation. Positional relationships of the

spatial triangles given by functions are analyzed

during this comparison .

3.2 Searching Symmetry Plane of

Model

As we assume that model’s normalization in coordi-

nate system is approximate, we try to transform co-

ordinates using small shifts and rotations by small an-

gles about the coordinateaxes. One process of surface

comparison may be implemented very efﬁciently so it

is possible to organize a guided search of such dis-

crete set’s transformation that provides the maximum

matching. The aim of this correction is to ﬁnd such

position of the Oyz symmetry plane that the value of

quantitative asymmetry estimation is minimum.

It can be assumed that we minimize estimation not

by all six parameters of elementary manipulations but

only by three of them because it is obvious that shifts

along the y and z axes doesn’t have an inﬂuence on

asymmetry estimation and we also don’t consider ro-

tation about the x axis as we have full face photogra-

phy.

We make small transformation of the coordinate

system: shift along the x axis, then rotation by the

angle ϕ about the z axis and, ﬁnally, rotation by the

angle ψ about the y axis. In such a way G

will trans-

form to G

(x, ϕ, ψ) and G

— to G

(x, ϕ, ψ). f and

g will also be transformed. Denote by Φ(x, ϕ, ψ) =

∆( f(x, ϕ, ψ), g(x, ϕ, ψ)) disparity measure between

transformed surfaces.

The problem of searching the optimal symmetry

plane reduces to minimization of Φ(x, ϕ, ψ). For this

purpose we use alternating-variable descent method

combining with algorithm of golden section.

Notice that function Φ is ravine, i.e. change δ of

variables ϕ or ψ causes a greater change of function

value than the same change δ of variable x. We are

taking into account this property of function during

minimization procedure.

In table 1 there are values of initial estimation of

facial asymmetry (after stage 1) and estimation after

symmetry plane correction for 4 different face models

of one person. To understand signiﬁcance of these

values let us remark that volume of ﬂuid in tablespoon

is approximately equal to 15000 cmm.

Table 1: Initial and corrected estimations of facial asymme-

try.

Model’s Initial asymmetry Corrected asym-

number estimation (cmm) metry estimation

(cmm)

1 47 466,361 24 072,518

2 49 192,110 25 205,272

3 43 473,767 24 421,316

4 46 280,040 22 263,813

An optimal shift along the x axis is about 2, 4−2, 6

mm for models from the database, values of optimal

angles about the y and z axes are about 0, 015 rad.

4 COMPUTING EXPERIMENTS

The described method for comparison of models was

implemented, and there also has been made multiple

computing experiments for all stages of algorithm.

As experimental estimations have shown, each of

stages, except stage of triangulation constructions,

is implemented in linear for number of mesh nodes

time. Delaunay triangulation is implemented in time

O(N logN). Triangulation construction deﬁnes com-

putational complexity of the proposed approach.

Running time for different stages of algorithm

during comparison of human’s face surfaces are ad-

duced in table (2). The three-dimensional portraits

consisting approximately from 3000 points were used

here. Computing experiments were conducted using

AMD Athlon 2600+ processor and 512 Mb operative

memory.

Results of computing experiments on the database

demonstrate that the proposed estimation is stable for

different models of one and the same person.

The experiments indicate that the initial estima-

tion varies strongly for several models od the same

person. Neverthelessthe stage of symmetry plane cor-

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

404

Table 2: Running time for different stages of algorithm.

Stage of algorithm Time (sec)

Construction of two triangulations 0,124

Construction of two MSTs 0,203

Location of triangulations 0,015

Function interpolation < 0,001

Construction of general triangulation 0,109

Computing disparity measure



− F



0,031

Total time 0,497

rection increases many times stability of the estima-

tion.

In average for the database spread in values of ini-

tial asymmetry estimation is 36 000-40000 cmm. On

the other hand, spread in values of corrected asymme-

try estimation is 9000-11000 cmm.

To estimate approximation accuracy of real head

model we perform the following experiments. We

compute change of asymmetry estimation of initial

model and model received by thinning, i.e. point re-

jection of the corresponding discrete set. Points for

rejection are selected randomly. Suppose make re-

jection of about 1 500 points of models consisted of

approximately 3 000 points; then asymmetry estima-

tion will not strongly change. After rejection of more

amount of points the asymmetry estimation begins in-

creasing (see Figure (3)).

Figure 3: Facial approximation accuracy.

5 CONCLUSIONS

In this paper we deﬁne a quantitative estimation to

compute facial asymmetry directly from 3D face

model. We introduce disparity measure between two

models and compare original face model and reﬂected

model. We propose algorithms to compute the estima-

tion and to determine the optimal symmetry plane of

model.

The proposed method has the following advan-

tages: computing efﬁciency, possibility of paralleling.

Besides, the described approach possesses some uni-

versality in comparison with others as it is suitable for

comparison of any models given by functions on dis-

crete sets. The proposed measure can be adapted for

each concrete application, for example, by means of

introducing measure on a surface.

The results of computing experiments carried out

on the database show stability of the proposed estima-

tion for different models of one and the same person

and numerical efﬁciency of the algorithm.

ACKNOWLEDGEMENTS

The authors are grateful to Gleb Gusev and Si-

mon Karpenko from ”Artec Group Company”

(http://artec-group.com) for given face models. The

research was supported by the Russian Foundation for

Basic Research (grants 08-01-00670, 08-07-00305-

a).

REFERENCES

Knizhnikov, Y. F., H. R. N. (2005). Application of digital

photogrammetry for diagnosing pathology of stereo-

scopic vision (in Russian). Society for Industrial and

Applied Mathematics.

Liu, Y., P. J. (2003). A quantiﬁed study of facial asymmetry

in 3d faces. In Robotics Institute, Carnegie Mellon

University, CMU-RI-TR-03-21. Pittsburgh, PA.

Mestetskiy, L., T. E. (2004). Delaunay triangulation: re-

cursion without space division of vertices (in russian).

In Graphicon 2004, International Conference on com-

puter graphics. Moscow.

Mitra, S., L. N. (2007). Understanding the role of facial

asymmetry in human face identiﬁcation. In Statistics

and Computing, Vol. 17, January, 2007, pp. 57 - 70.

Murynin, A. B., K. V. F. (2004). Estimation of bilateral fa-

cial symmetry breaking using a stereoscopic computer

vision system. In Graphicon 2004, International Con-

ference on computer graphics. Moscow.

Teng, K. (2006). Expression classiﬁcation using wavelet

packet method on asymmetry faces. In tech. report

CMU-RI-TR-06-03, Robotics Institute. Carnegie Mel-

lon University.

ESTIMATION OF ASYMMETRY IN 3D FACE MODELS

405