REAL-TIME PIECEWISE PERSPECTIVE PROJECTIONS

Haik Lorenz and J

urgen D

ollner

Hasso-Plattner-Institute, University of Potsdam, Germany

Keywords:

Non-planar projections, Geometry shaders, Geometry ampliﬁcation, Non-photorealistic rendering.

Abstract:

This paper presents an approach to real-time rendering of non-planar projections with a single center and

straight projection rays. Its goal is to provide optimal and consistent image quality. It operates entirely in

object space to remove the need for image resampling. In contrast to most other object-space approaches, it

does not evaluate non-linear functions on the GPU, but approximates the projection itself by a set of perspective

projection pieces. Within each piece, graphics hardware can provide optimal image quality. The result is a

coherent and crisp rendering. Procedural textures and stylization effects greatly beneﬁt from our method as

they usually rely on screen-space operations. The real-time implementation runs entirely on GPU. It replicates

input primitives on demand and renders them into all relevant projection pieces. The method is independent of

the input mesh density and is not restricted to static meshes. Thus, it is well suited for interactive applications.

We demonstrate it for an analytic and a freely designed projection.

1 INTRODUCTION

The pinhole camera model is the most widely used

model for depicting three-dimensional worlds. To-

day’s graphics hardware is tailored to the underlying

projection types: planar perspective or orthographic

projections. Nonetheless, numerous applications in

computer graphics require other, non-pinhole projec-

tion types:

• They are inevitable when using non-planar dis-

plays, such as cylindrical or spherical walls, to

compensate for distortions (Jo et al., 2008).

• Some natural phenomena, such as caustics, reﬂec-

tions, or refractions off curved surfaces, can be

described by a projection (Wei et al., 2007).

• They can also deliberately introduce distortions

to provide improved perception of a virtual en-

vironment. This includes increased ﬁeld of view

and lens effects (Popescu and Aliaga, 2006; Brosz

et al., 2007).

• Arts and non-photorealism achieve dramatic ef-

fects using irregular projections (Wood et al.,

1997; Agrawala et al., 2000; Glassner, 2004a;

Glassner, 2004b).

• Images of particular projection types serve as stor-

age for parts of the plenoptic function (Rade-

macher and Bishop, 1998). Most commonly,

these are cubical, spherical, or paraboloidal im-

ages used for rendering reﬂections or refractions

in real-time (Heidrich and Seidel, 1998; Wan

et al., 2007).

Non-pinhole projections have been discussed exten-

sively in literature, resulting in various camera mod-

els, e.g., (L

offelmann and Gr

oller, 1996; Yu and

McMillan, 2004; Brosz et al., 2007). They cannot be

rendered directly with today’s graphics hardware. In-

stead, ray-tracing is commonly used (L

offelmann and

oller, 1996). A large body of work exists on imple-

menting ray-tracing on GPU for various phenomena

and scene conditions. (Popov et al., 2007; Wei et al.,

2007) present recent approaches and good surveys of

related methods. Mostly, they use the GPU as power-

ful stream processor instead of as rasterization device

and thus rarely beneﬁt from built-in capabilities such

as anisotropic texture ﬁltering, perspective-correct in-

terpolation, or screen-space derivatives.

This paper focuses on enabling these high qual-

ity rasterization capabilities of current GPUs for non-

pinhole projections. Our approach achieves a signiﬁ-

cantly improved and consistent image quality regard-

less of the input mesh while maintaining real-time

performance (Fig. 1). In particular, we do not use ray

tracing or image resampling, but directly render the

non-pinhole projection. At the same time, we enable

the rasterization hardware to work under perspective

projections exclusively and hence with optimal qual-

147

Lorenz H. and Döllner J. (2009).

REAL-TIME PIECEWISE PERSPECTIVE PROJECTIONS.

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 147-155

DOI: 10.5220/0001786401470155

 SciTePress

Figure 1: A 360

◦

cylindrical view of a city rendered using

a piecewise perspective projection. The city model contains

35,000 triangles and the view uses 160 pieces. At a resolu-

tion of 1600 × 1200, an NVidia 8800GTS achieves 55 fps

with 16x anisotropic texture ﬁltering and 16x antialiasing.

Our technique enables the use of screen-space-dependent

rendering effects such as solid wireframe (Bærentzen et al.,

2006) or pen-and-ink style (Freudenberg et al., 2001).

ity. As a result, procedural textures and stylization

effects can be used instantly regardless of the actual

projection. These properties are achieved by approx-

imating the non-pinhole projection through a set of

connected but disjoint perspective projections. This

construction limits our approach to projections with a

single center and straight projection rays (Single Cen-

ter Of Projection – SCOP).

1.1 Real-time Scop on Gpu

A straightforward and efﬁcient approach to real-

time single-center projections is the implementation

as image-based post-processing effect (Yang et al.,

2005; Trapp and D

ollner, 2008). The rendering con-

sists of two steps: First, a perspective projection is

rendered into an offscreen buffer. Second, this buffer

is used as texture for rendering a deformed mesh.

The offscreen buffer can contain a cube map to en-

able 360

◦

views. This approach is capable of ren-

dering all SCOP effects. It is image-based since the

actual deformation happens after, not during, render-

ing the scene. Its advantages are easy implementation

and good support by graphics hardware. The major

drawback is image quality. The resampling in step

two inevitably introduces blurring artifacts that espe-

cially degrade edges, detailed geometry, procedural

textures, and stylization effects. Today’s hardware ca-

pability of antialiasing through multi-sampling does

not improve image quality substantially as it applies

before resampling.

Object-space approaches do not suffer from im-

age resampling artifacts as they render the image

directly. A simple solution is applying the non-

pinhole projection in the vertex shader (Spindler et al.,

2006). Then a triangle’s vertices are projected cor-

rectly, but the interior and edges are rasterized in-

correctly in a linear fashion. This is acceptable as

long as a triangle’s size on screen and thus the ras-

terization error is limited. Hence, interactive environ-

ments require dynamic reﬁnement. Approaches in-

clude precomputed static levels of detail (Sander and

Mitchell, 2005), progressive meshes (Hoppe, 1996),

adaptive mesh reﬁnement (Boubekeur and Schlick,

2008; Tatarinov, 2008), dynamic mesh reﬁnement

(Lorenz and D

ollner, 2008), or hardware tessellation

units (Tatarchuk, 2007; Casta

no, 2008). They vary

in the distribution of computation between CPU and

GPU. The rendered mesh must be free of T-junctions

to prevent artifacts due to correct vertex location but

incorrect edge rasterization. Even with reﬁnement,

the incorrect rasterization greatly ampliﬁes Z-Buffer

artifacts, such as inaccurate near plane clipping and

interpenetrations of parallel triangles. A solution is

emitting correct depth values in the fragment shader.

This reduces depth test performance and increases

fragment processing overhead due to a disabled early

z-test (Persson, 2007).

A more sophisticated solution is using non-linear

rasterization. Since the rasterizer is a hardwired com-

ponent, (Hou et al., 2006) and (Gascuel et al., 2008)

render a bounding shape for each primitive and use

ray intersection in a fragment shader to compute

the correct fragment and all its attributes under non-

pinhole projections. As a consequence, these meth-

ods cannot beneﬁt from high quality screen-space-

dependent operations built into modern graphics hard-

ware, such as mipmapping, anisotropic ﬁltering, or

screen-space derivatives.

1.2 Piecewise Perspective Projection

Overview

Piecewise perspective projections use an idea pro-

posed in (Hou et al., 2006): simplify a complex pro-

jection by a set of pieces with simpler projections.

The pieces’ projection frusta are connected but dis-

joint with their union approximating the original pro-

jection volume. (Hou et al., 2006) rely on trian-

gle cameras, simple non-pinhole projections, which

makes them capable of rendering multi-perspective

views but prevents them from exploiting hardware

functionality. We restrict the projection pieces to us-

ing perspective projections exclusively, which limits

our technique to SCOP effects.

Key advantage of our construction compared to

all other object-space approaches is the absence of

non-linearities during rasterization. All non-linear as-

pects of the non-pinhole projection are encoded into

the layout of the piecewise approximation. Con-

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

148

sequently, rasterization and all high quality screen-

space-dependent operations work with optimal qual-

ity within each piece. Similarly, existing shaders, par-

ticularly procedural textures and stylization effects,

can be used instantly. The resulting images do not

exhibit blurring artifacts and capture the non-pinhole

projection regardless of the input mesh and rendering

effect. There is no need for reﬁnement. In addition,

Z-buffer artifacts are not ampliﬁed.

The increase in image quality comes at the cost of

increased geometry processing overhead. Each prim-

itive needs to be rendered into each projection piece it

is visible in. Hence, it needs to be processed multiple

times per frame. Depending on the number of pieces

in an approximation, this can result in a substantial

overhead.

The remaining paper is organized as follows: the

next section describes the idea of piecewise perspec-

tive projections in depth and devises a real-time im-

plementation using geometry shaders. Section 3 pro-

vides two example applications. Section 4 provides

experimental results and compares them to alternative

approaches. Section 5 concludes.

2 PIECEWISE PERSPECTIVE

PROJECTION

The key idea of piecewise perspective projections is

the approximation of a non-pinhole projection vol-

ume by a set of connected but disjoint perspective pro-

jection frusta, i.e., projection pieces. Each projection

piece uses a regular perspective projection clipped to

the piece’s boundaries for image formation. Thus,

the rendering encounters no non-linearities and hard-

ware rasterization generates a correct image at opti-

mal quality for each piece. The combination of all

piece images creates an approximation of the desired

non-pinhole projection. The number of pieces deﬁnes

the quality of approximation.

For implementing this idea, three challenges need

to be addressed:

1. approximation of the non-pinhole projection with

projection pieces,

2. rendering of a primitive in all projection pieces it

is visible in, and

3. clipping of a primitive’s rendering to the projec-

tion piece’s boundaries.

Approximation. An artifact-free approximation is

only possible for SCOP effects, as other projections

lead to overlapping piece frusta. In general, each pro-

jection piece p uses an individual projection matrix

(p), such that neighboring pieces produce match-

ing renderings at their shared boundary. Matrix com-

putation depends on the particular projection and hap-

pens once in a preprocessing step. Two typical ap-

proaches are exempliﬁed in Section 3.

Rendering. A simple implementation renders the

whole model for each projection piece with the re-

spective projection matrix and clipping in effect. Ren-

dering should use additional culling to account for a

projection piece’s small screen area but does not re-

quire any change to shaders or meshes to deal with a

non-pinhole projection.

Clipping. Clipping can rely on viewport clipping

if all pieces are rectangular or on user clip planes

for convex pieces. Since both possibilities are per-

formed by the rasterization hardware, no explicit clip-

ping needs to be implemented in a shader. The result-

ing piece images are non-overlapping and thus they

can be rendered directly to the framebuffer without

the need for a dedicated composition step.

Our method can reproduce the same projection ef-

fects as the image-based approach of (Yang et al.,

2005). Their intermediate rendering uses a perspec-

tive projection described by a matrix M

. The mesh

used for deforming this rendering implicitly deﬁnes

an afﬁne transformation M(t) from the source area of

each triangle t to the screen. An equivalent piecewise

perspective projection can be constructed by clipping

a perspective projection M(t) ∗ M

to the deformed

triangle’s boundaries for all triangles t.

The simple implementation mentioned above suf-

fers from increased CPU load due to additional

culling and a large number of draw calls. At the same

time, GPU efﬁciency is reduced as each draw call ren-

ders to a small screen portion only. Thus, rendering

becomes CPU-bound and real-time performance is

limited to projection approximations with very small

piece counts.

2.1 Real-time Implementation

Our real-time implementation reverses the rendering

approach to make it GPU-friendly. Instead of deter-

mining all primitives for a projection piece, we deter-

mine all relevant, i.e., covered, pieces for a primitive.

We can then render the ﬁnal image in a single draw

call by replicating each primitive to all its relevant

pieces. Texture buffers allow for changing the pro-

jection matrix within this draw call. User clip planes

cannot be updated that way. The alternative is to de-

ﬁne a standard clip space with ﬁxed clip planes and

provide a transformation from camera space to clip

space for each projection piece.

REAL-TIME PIECEWISE PERSPECTIVE PROJECTIONS

149

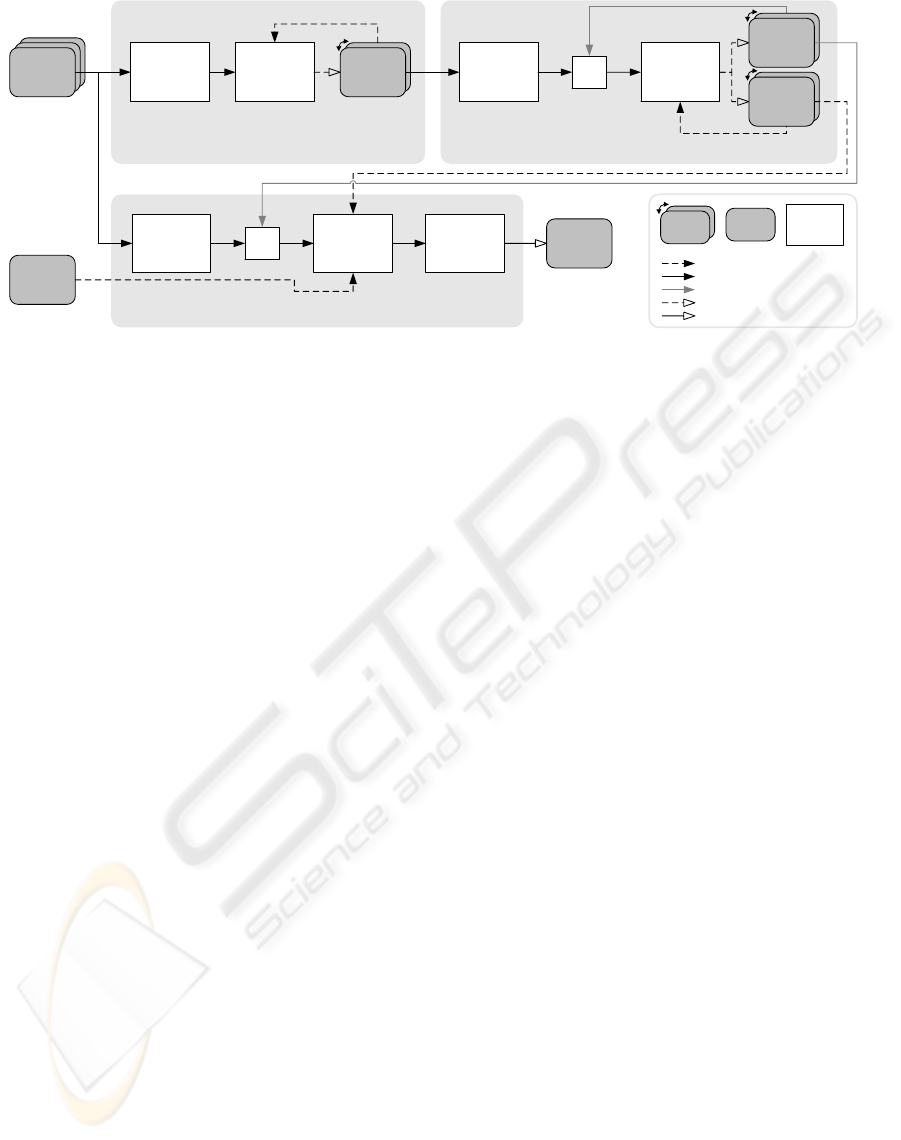
pass 3: indexed rendering

each original primitive is passed as point with all attributes into the rendering pipeline and indexed

by the primitive index; a geometry shader convertes each replication into a rendering primitive

primitive

attributes

vertex shader

geometry shader

(in: points,

out: any primitive)

vertex

cache

fragment shader

GL_POINTS

gl_PrimitiveIDIn

per-primitive

repetition

count

vertex shader

geometry shader

(in: any primitive,

out: points)

per-primitive

replication

count

pass 1: amplification calculation

calculates and writes one replication count per input primitive

gl_PrimitiveIDIn

repetition

numbers

pass 2: primitive index update

uses the existing primitive index as index into replication

counts; each copy of a replication count generates a fraction of the new primitive index

vertex

cache

primitive

index

vertex shader

geometry shader

(in: points,

out: points)

GL_POINTS

gl_PrimitiveIDIn

read as buffer texture (index at tip)

read as attribute / varying

write through transform feedback

write through raster operation

framebuffer

buffer

shader

ping-pong

buffer

read as index

projection &

clip matrices

f(replication number)

replication

numbers (e.g.

0,1,0,0,1,2,…)

primitive

index (e.g.

0,0,1,2,2,2,…)

Figure 2: Primitive replication algorithm overview and data ﬂow. Pass 3 can implement any rendering effect.

Since a primitive can ﬁll the whole screen, the

maximum replication count is the projection piece

count. Hence, a straight forward replication using

geometry shaders, which are currently limited to at

most 128 output vertices, is not possible. In (Lorenz

and D

ollner, 2008) a solution to a similar problem has

been described. They use a ﬁxed three-pass scheme

for per-primitive view-dependent tessellation on GPU

and achieve arbitrary and unbounded geometry am-

pliﬁcation without CPU intervention. Core of their

scheme is a continuously updated intermediate mesh

of barycentric subtriangles. This transforms the ge-

ometry shader’s output limit from a mesh size limit

to a per-frame growth limit. Since we only require

replicated, not tessellated, primitives, we replace their

intermediate mesh with a primitive index and accom-

panying replication numbers. Both are stored in sep-

arate ping-pong buffers. The primitive index works

similar to a traditional vertex index. The accompa-

nying replication number consecutively numbers all a

single primitive’s occurences in the index. Together,

they enable indexed access to a primitive’s vertex at-

tributes in the vertex shader (e.g., by passing all 3 po-

sitions for a triangle at once) but also allow for distin-

guishing replications of a single primitive in the ge-

ometry shader.

In the following, we provide a brief description

of the rendering process (Fig. 2). For details, re-

fer to (Lorenz and D

ollner, 2008). In the ﬁrst pass,

all original primitives are processed by a geometry

shader to determine the number of covered projec-

tion pieces. This information is stored in a buffer us-

ing transform feedback. The second pass takes the

previous frame’s primitive index and produces a new

primitive index and matching replication numbers,

such that each primitive is replicated according to the

counts calculated in pass 1. Pass 3 ﬁnally renders

all replicated primitives. It uses the primitive index

to fetch all a primitive’s vertex attributes from vertex

buffers and the replication number to select the pro-

jection piece with projection and clip matrix. Addi-

tional vertex, geometry and fragment processing can

implement any effect as if no piecewise perspective

projection was in effect. Thus, existing shaders are

easily incorporated.

This scheme applies to arbitrary “primitive soups”

of any type since no connectivity information or topo-

logical restriction is assumed. Key for rendering is

the determination of covered projection pieces (pass

1) and their enumeration (pass 3). Both depend on the

desired non-pinhole projection. Two aspects need to

be considered. First, while rendering primitives to ir-

relevant pieces does not inﬂuence image quality, it de-

grades performance since additional replications are

created and processed only to become clipped again.

Thus, the determination is not required to be exact,

but should be a good estimation. Second, given a

primitive and its replication number, the target pro-

jection piece needs to be identiﬁed in O(1) time in a

shader (function f () in Fig. 2). The mapping can be

supported by additional information generated in pass

1. In the following, we present two approaches.

3 APPLICATIONS

Our real-time implementation involves two appli-

cation-dependent parts: projection piece deﬁnition

and coverage determination/enumeration. We demon-

strate the use for two typical applications: a horizon-

tal cylindrical projection, which can be described an-

alytically, and texture-based view deformation, which

improves the camera texture technique of (Spindler

et al., 2006).

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

150

3.1 Cylindrical Projection

A horizontal cylindrical projection uses a perspective

projection in the vertical direction but a non-planar

projection horizontally. Thus, it sufﬁces to limit the

horizontal edge length to control an approximation’s

quality. The piecewise perspective projection then

splits the curved projection volume into narrow rect-

angular slices. Figure 3 sketches this setting.

cylindrical

projection volume

piecewise perspective

approximation

projection surface

projection planes

Figure 3: Top-down view of the cylindrical projection vol-

ume and its approximation with perspective projections.

Projection piece coverage determination and enu-

meration for rendering is rather simple as a single

primitive normally covers a consecutive range of pro-

jection pieces. It sufﬁces to ﬁnd the leftmost and

rightmost point of the primitive’s projection and ren-

der it to all pieces in between. A special case oc-

curs when cylinder axis and primitive intersect. In

that case, the primitive is potentially visible in all pro-

jection pieces. Finally, wrap-arounds require special

care. In the end, pass 1 outputs both the start piece

index (which can be to the right of the end index)

and piece count. Pass 3 uses a primitive’s replication

number plus the start index modulo n – the number of

projection pieces – as target projection piece.

The projection matrix M of a piece p can be de-

scribed by a series of transformations:

M(p) = M

(p) ∗ M

∗ M

(p) (1)

rotates the center axis of a projection piece about

the y axis onto the negative z axis. M

is a perspective

projection matrix with a horizontal ﬁeld of view ϕ

/n, where ϕ

denotes the cylindrical ﬁeld of view.

scales the standard postprojective space to ﬁt the

piece’s width on the screen. M

ﬁnally moves the

piece’s projection from the screen center to its actual

location on screen.

Clipping requires a standard clip space to enable

ﬁxed clip planes. The following transformation leads

to such a space:

clip

(p) = M

;1) ∗ M

(p) (2)

is a scaling operation that uses the ﬁrst (M

)

and second (M

) value from the projection matrix’s

diagonal. The complete transformation effectively

transforms into the normalized space used for per-

spective division. The corresponding four clip planes

deﬁne an inﬁnite pyramid with the tip being located in

the origin and the opening pointing down the negative

z axis with an opening angle of 90

◦

both vertically

and horizontally.

Figure 4: Rendering of a object-space 360

◦

cylindrical pro-

jection with overlayed wireframe. Piece borders are marked

with black lines.

Fig. 4 depicts a sample image with highlighted

piece boundaries and primitive edges. For clarity, it

uses only 40 pieces. Experiments show, that pieces

of width 10-20 pixels provide a good approximation.

The average replication count is less than 2, while the

maximum replication is the total piece count n.

3.2 Texture-based View Deformation

View deformation (Trapp and D

ollner, 2008) uses one

or more standard perspective views (e.g. a cube map)

and distorts them to create the ﬁnal image. The distor-

tion is either analytical, such as a paraboloid mapping,

or freely deﬁned, such as camera textures (Spindler

et al., 2006). Both approaches use a rectangular two-

dimensional grid in the perspective view(s) and map

it to a deformed mesh on the screen. The construc-

tion of a piecewise perspective projection follows the

description in Section 2. In the following, we pro-

vide details for an improved implementation of cam-

era textures. They encode the distortion as offset vec-

tors in a 2D texture (Figure 5). A point’s deformed

projection is found by using its perspective projection

for texture lookup and adding the resulting offset vec-

tor to that perspective projection. In contrast to the

original implementation, ours is independent of mesh

density. Regardless of a primitive’s projected size, all

details of the distortion are captured in the primitive’s

interior.

Piecewise perspective projections require splitting

the rectangular grid into triangles. Even though it is

possible to specify a projective mapping from a two-

dimensional rectangle to an arbitrary quadrangle, it

is not possible to guarantee a matching mapping for

REAL-TIME PIECEWISE PERSPECTIVE PROJECTIONS

151

camera

texture

input grid

distorted grid

Figure 5: Projection plane splitting and subsequent distor-

tion using a 16 × 16 pixel camera texture. The model is

rendered directly into the distorted grid.

shared edges. This property would require a bilin-

ear transformation (Heckbert, 1989) current raster-

izers cannot deal with. Splitting the rectangle into

two triangles leads to two afﬁne transformations and

a continuous approximation. Nevertheless, consider-

ing pairs of triangluar projection pieces as one cell is

beneﬁcal regarding coverage determination and enu-

meration. It enables operating on a simple rectangular

grid in pass 1. View deformation is irrelevant to pass

1 as it does not change visibility. Pass 2 replicates

primitives for cells. Pass 3 ﬁnally emits each primi-

tive twice – once for each triangle in a cell – with the

respective transformation matrices in effect.

A simple solution to determining the coverage of a

primitive is using its bounding box in the undistorted

projection plane. All cells intersected by the bound-

ing box are considered as being covered. Thus, the

output of pass 1 is the position of the lower left cell

and width w and height h of the bounding box in

cell units. For efﬁcient storage, all four values use 16-

bit integers and are packed into two 32-bit integers.

Pass 3 can map the replication number r to a cell at

position (c

.x + r mod w ; c

.y +

r/w

). This two-

dimensional index can be used for lookup in a tex-

ture containing the afﬁne transformation matrices for

both projection pieces in this cell. Since the bounding

box coverage determination is very conservative, we

added culling to pass 3 to discard invisible primitives

before rasterization setup.

The derivation of afﬁne transformation matrices

can be found in (Heckbert, 1989). During rendering,

it is applied subsequent to the original model-view-

projection matrix. Clipping uses a similar approach

as the cylindrical projection. Here, only three clip

planes are in effect, where two neighboring planes of

the pyramid described above are removed and the new

third one is a diagonal. To clip both pieces of one cell

to the same clip planes, one piece’s clip coordinates

are rotated about the z axis by 180

◦

Fig. 6 shows a 128 × 128 camera texture applied

to a view of a city model. A thin black wireframe indi-

cates the triangular projection cells, thick white lines

highlight primitive edges. Even for this moderate tex-

ture size, such a rendering easily requires 1,000,000

Figure 6: Rendering using the camera texture shown in Fig.

5 at a resolution of 128×128. Thin black lines indicate pro-

jection pieces. Thick white lines highlight primitive edges.

triangles while the model only contains about 35,000

primitives. Our implementation of texture-based view

deformation allows for animating the deformation ef-

fect, as this only involves updating the matrices.

4 RESULTS

We compare our object-space technique for both ap-

plications presented in Section 3 to their image-based

implementations. All implementations use native

OpenGL 2.0 with relevant extensions. All measure-

ments have been taken on a desktop PC running Win-

dows XP with an AMD Athlon 64 X2 4200+ proces-

sor, 2GB RAM, and an NVidia GeForce 8800 GTS

with 640 MB RAM. The tests use a path through

the textured city model data shown in Figures 4 and

6. It consists of 35,000 triangles in 14 state groups.

The viewport resolution is 1600 × 1200. In contrast

to (Lorenz and D

ollner, 2008), no latency hiding has

been used since it showed no improvements. Besides

the frame rate, we provide the number of triangles

used for rendering (av. tri count), their replication

ratio to the original triangle count (av. repl. ratio),

and the total size of all vertex buffers used for render-

ing (Vbuf). High quality (HQ) measurements use 16x

anisotropic texture ﬁltering and 16xQ antialiasing.

Table 1: Rendering statistics for the 360

◦

cylindrical cam-

era. Our piecewise perspective projection (PPP) outper-

forms the image-based implementation (IB).

Impl Fps Av. tri Av. repl. Vbuf

count ratio (kB)

IB 41.7 21,151 0.61 1,081

PPP 84.7 67,675 1.96 2,672

IB HQ 33.8 21,151 0.61 1,081

PPP HQ 54.8 67,675 1.96 2,672

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

152

The image-based implementation of the 360

◦

cylindrical camera uses a dynamic 2048 ×2048 cube-

map that is created in a single pass through lay-

ered rendering. It implements frustum and backface

culling in the geometry shader (Persson, 2007) which

explains the replication count less than 1. The piece-

wise perspective projection uses strips of 10 pixels,

i.e., 160 pieces, for approximation. On average, each

triangle is visible in only two strips. The increased

memory footprint results from the intermediate mesh,

which requires 16 bytes per rendered primitive. In

total, our method outperforms the image-based ap-

proach while providing higher image quality (Fig.

7). Even for smaller cubemaps, the image-based ap-

proach does not overtake ours, but image quality fur-

ther degrades.

Figure 7: Comparision of image quality for cylindrical pro-

jection. Closeups of screen shots for PPP (left) and IB

(right). Top: pen-and-ink style, bottom: depth-dependent

solid wireframe.

Table 2: Rendering statistics for the view deformation with

a 128 × 128 camera texture. While achieving signiﬁcantly

better image quality, performance can not compete with the

image-based approach.

Impl Fps Av. tri Av. repl. Vbuf

count ratio (kB)

IB 206.2 34,596 1 1,081

PPP 8.4 727,982 21.04 13,858

IB HQ 95.8 34,596 1 1,081

PPP HQ 8.2 727,982 21.04 13,858

For the texture-based view deformation, the

image-based technique uses only a 2D texture, no

cubemap. Therefor, it achieves higher frame rates

than for the cylindrical projection. In contrast, our

method needs to render a signiﬁcantly higher amount

of triangles, which translates to a severely reduced

speed. Each input triangle spans on average about 21

of the 32,258 projection pieces. While delivering in-

teractive frame rates, the vertex processing overhead

is substantial. The bottleneck is pass 3. Primitive

replication performed in pass 1 and 2 accounts for

only 6% of the total workload. Consequently, a more

aggressive coverage determination than the bounding

box test could signiﬁcantly improve performance. In

addition, a projection piece size of 20 × 20 pixels suf-

ﬁces for good approximations, i.e., the camera texture

resolution should be adapted to the viewport resolu-

tion. In our example, using a suitable 80 × 60 camera

texture increases the frame rate to 22.1 fps (HQ: 20.9

fps) at an av. tri count of 351,954. Figure 8 shows the

improved image quality.

Figure 8: Comparision of image quality for texture-based

view deformation. Closeups of screen shots for PPP (left)

and IB (right). Top: pen-and-ink style, bottom: depth-

dependent solid wireframe.

5 CONCLUSIONS

This paper has presented a novel object-space ap-

proach to rendering non-pinhole projections with a

single projection center. The piecewise perspective

projection technique removes non-linearities from

rendering by approximating a projection with a set

of perspective projections. The distorted image is

formed directly on screen without intermediate ren-

dering steps. As a result, all image quality opti-

mizations provided by modern graphics hardware that

assume a perspective projection continue to operate

with regular precision. Particularly, antialiasing, pro-

cedural textures, and stylization effects proﬁt from

our technique. It can be implemented on any graph-

ics hardware but requires DirectX10 features for real-

time performance. Core is on-demand replication of

primitives on the GPU using geometry shaders and

transform feedback, such that a primitive is rendered

into only those projection pieces it actually covers.

The technique’s drawback is a high geometry pro-

cessing overhead. Primitive replication itself is rather

efﬁcient. The major bottleneck is vertex processing in

pass 3 since a rendered primitive covers at most one

projection piece. In the example with a 128 × 128

REAL-TIME PIECEWISE PERSPECTIVE PROJECTIONS

153

pixel view deformation texture, up to 1,000,000 tri-

angles are needed for rendering a frame. In the fu-

ture, we seek to improve the performance of pass 3

both by better coverage determination and exploita-

tion of hardware caches during processing of repli-

cated primitives. A second direction of research is

evaluating applicability to other types of projections,

such as slit or pushbroom cameras. The rendering

scheme might also prove useful for other algorithms,

e.g., (Hou et al., 2006). Finally, future graphics

hardware will include an additional tessellation unit

(Casta

no, 2008), which might enable a single-pass

implementation of piecewise perspective projections.

ACKNOWLEDGEMENTS

This work has been funded by the German Federal

Ministry of Education and Research (BMBF) as part

of the InnoProﬁle research group “3D Geoinforma-

tion” (www.3dgi.de).

REFERENCES

Agrawala, M., Zorin, D., and Munzner, T. (2000). Artistic

multiprojection rendering. In Proc. of the Eurograph-

ics Workshop on Rendering Techniques 2000, pages

125–136. Springer-Verlag.

Bærentzen, A., Nielsen, S. L., Gjøl, M., Larsen, B. D., and

Christensen, N. J. (2006). Single-pass wireframe ren-

dering. In ACM SIGGRAPH 2006 Sketches, page 149.

ACM.

Boubekeur, T. and Schlick, C. (2008). A ﬂexible kernel for

adaptive mesh reﬁnement on GPU. Computer Graph-

ics Forum, 27(1):102–114.

Brosz, J., Samavati, F. F., Sheelagh, M. T. C., and Sousa,

M. C. (2007). Single camera ﬂexible projection. In

Proc. of NPAR ’07, pages 33–42. ACM.

Casta

no, I. (2008). Tesselation of displaced subdivision sur-

faces in DX11. In XNA Gamefest 2008.

Freudenberg, B., Masuch, M., and Strothotte, T. (2001).

Walk-through illustrations: Frame-coherent pen-and-

ink in game engine. In Proc. of Eurographics 2001,

pages 184–191.

Gascuel, J.-D., Holzschuch, N., Fournier, G., and P

eroche,

B. (2008). Fast non-linear projections using graphics

hardware. In Symposium on Interactive 3D graphics

and games SI3D ’08, pages 107–114. ACM.

Glassner, A. S. (2004a). Digital cubism. IEEE Computer

Graphics and Applications, 24(3):82–90.

Glassner, A. S. (2004b). Digital cubism, part 2. IEEE Com-

puter Graphics and Applications, 24(4):84–95.

Heckbert, P. S. (1989). Fundamentals of texture mapping

and image warping. Technical report, University of

California at Berkeley, Berkeley, CA, USA.

Heidrich, W. and Seidel, H.-P. (1998). View-independent

environment maps. In HWWS ’98: Proc. of the ACM

SIGGRAPH/EUROGRAPHICS workshop on Graph-

ics hardware, pages 39–45. ACM.

Hoppe, H. (1996). Progressive meshes. In Proc. of SIG-

GRAPH ’96, pages 99–108. ACM.

Hou, X., Wei, L.-Y., Shum, H.-Y., and Guo, B. (2006).

Real-time multi-perspective rendering on graphics

hardware. In EUROGRAPHICS Symposium on Ren-

dering. Blackwell Publishing.

Jo, K., Minamizawa, K., Nii, H., Kawakami, N., and Tachi,

S. (2008). A GPU-based real-time rendering method

for immersive stereoscopic displays. In ACM SIG-

GRAPH 2008 posters, page 1. ACM.

offelmann, H. and Gr

oller, E. (1996). Ray tracing with

extended cameras. Journal of Visualization and Com-

puter Animation, 7(4):211–227.

Lorenz, H. and D

ollner, J. (2008). Dynamic mesh reﬁne-

ment on GPU using geometry shaders. In Proc. of the

16th WSCG.

Persson, E. (2007). ATI radeon HD2000 programming

guide. Technical report, AMD, Inc.

Popescu, V. and Aliaga, D. G. (2006). The depth discon-

tinuity occlusion camera. In SI3D, pages 139–143.

ACM.

Popov, S., Gunther, J., Seidel, H.-P., and Slusallek, P.

(2007). Stackless kd-tree traversal for high perfor-

mance gpu ray tracing. Computer Graphics Forum,

26:415–424.

Rademacher, P. and Bishop, G. (1998). Multiple-center-of-

projection images. In SIGGRAPH, pages 199–206.

Sander, P. V. and Mitchell, J. L. (2005). Progressive Buffers:

View-dependent Geometry and Texture for LOD Ren-

dering. In Symposium on Geometry Processing, pages

129–138. Eurographics Association.

Spindler, M., Bubke, M., Germer, T., and Strothotte,

T. (2006). Camera textures. In Proc. of the 4th

GRAPHITE, pages 295–302. ACM.

Tatarchuk, N. (2007). Real-time tessellation on GPU. In

Course 28: Advanced Real-Time Rendering in 3D

Graphics and Games. ACM SIGGRAPH 2007.

Tatarinov, A. (2008). Instanced tessellation in DirectX10.

In GDC ’08: Game Developers’ Conference 2008.

Trapp, M. and D

ollner, J. (2008). A generalization approach

for 3d viewing deformations of single-center projec-

tions. In Proc. of GRAPP 2008, pages 162–170. IN-

STICC Press.

Wan, L., Wong, T.-T., and Leung, C.-S. (2007). Isocube:

Exploiting the cubemap hardware. IEEE Trans. on

Vis. and Comp. Graphics, 13(4):720–731.

Wei, L.-Y., Liu, B., Yang, X., Ma, C., Xu, Y.-Q., and Guo,

B. (2007). Nonlinear beam tracing on a GPU. Tech-

nical report, Microsoft, MSR-TR-2007-168.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

154

Wood, D. N., Finkelstein, A., Hughes, J. F., Thayer,

C. E., and Salesin, D. H. (1997). Multiperspective

panoramas for cel animation. In Proc. of ACM SIG-

GRAPH ’97, pages 243–250. ACM Press/Addison-

Wesley Publishing Co.

Yang, Y., Chen, J. X., and Beheshti, M. (2005). Nonlinear

perspective projections and magic lenses: 3d view de-

formation. IEEE Comput. Graph. Appl., 25(1):76–84.

Yu, J. and McMillan, L. (2004). General linear cameras. In

ECCV (2), volume 3022 of Lecture Notes in Computer

Science, pages 14–27. Springer.

REAL-TIME PIECEWISE PERSPECTIVE PROJECTIONS

155