
MULTI-PERSPECTIVE PANORAMAS OF URBAN SCENES
WITHOUT SAMPLING ERRORS
Siyuan Fang and Neill Campbell
Department of Computer Science, University of Bristol, U.K.
Keywords:
Image Based Rendering, Multi-perspective panorama, City Visualization.
Abstract:
In this paper we introduce a framework for producing multi-perspective panoramas of urban streets from
a dense collection of photographs. The estimated depth information are used to remove sampling errors
caused by depth parallax of non-planar scenes. Then, different projections are automatically combined to
create the multi-perspective panorama with minimal aspect ratio distortions, which is achieved by a two-phase
optimization: firstly, the global optimal configuration of projections is computed and then a local adjustment
is applied to eliminate visual artifacts caused by undesirable perspectives.
1 INTRODUCTION
Rendering a street usually needs to combine differ-
ent input photographs, as the field of view of a sin-
gle photograph is limited to a portion of the street.
Traditional image mosaicing techniques (Szeliski and
Shum, 1997; Shum and Szeliski, 2000) assume in-
put images are captured at a single viewpoint. In
this case, the input images can be registered based
on certain alignment models, e.g., the homography.
However, it is usually impossible to place the view-
point far enough to encompass the entire street. To
acquire more scenes, we need to change the view-
point of the camera. Generating panoramas from im-
ages captured at different viewpoints is much more
challenging as an uniform alignment model for non-
planar scenes does not exist. In this paper, we present
a framework for constructing panoramas from image
sequences captured from a moving camera.
Recently, many approaches have been proposed
to combine images captured at different viewpoints
into a panoramic mosaic. These approaches can be
grouped into the following three categories:
View Interpolation. These approaches warp pix-
els from input images to a reference viewpoint us-
ing the pre-computed 3D scene structure (Chen and
Williams, 1993; Kumar et al., 1995). There are two
main problems with these approaches: to establish an
accurate correspondence between images for stereo is
still a hard vision problem, and there will likely be
holes in the result image due to sampling issues of the
forward mapping and the occlusion problem.
Optimal Seam. These approaches (Davis, 1998;
Agarwala et al., 2006) formulate the composition into
a labeling problem, i.e., pixel values are chosen to
be one of the input images. To avoid discontinuity,
the partition of different labeling is searched to min-
imize certain cost metrics such as pixel value differ-
ence. However, for scenes with large depth variations,
it is often impossible to find such an optimal partition
that can create seamless mosaics.
Strip Mosaic. The basic idea of the strip mosaic
is to cut a thin strip from a dense collection of im-
ages and put them together to form a panorama. In
the push-broom model (Zhu et al., 2001; Zheng,
2003), the result image exhibits parallel in one direc-
tion and perspective in the other, while the crossed-
slits (Zomet et al., 2003) model is perspective in one
direction and is perspective from a different view-
point in the other direction. The aspect ratio dis-
tortion is inherent due to the different projections
along the two directions. Moreover, since the pin-
hole camera is used to capture input images, the re-
sult exhibits sampling errors due to the depth paral-
lax. By combining different projection models, multi-
perspective panoramas can be synthesized, e.g., (Ro-
man et al., 2004; Wexler and Simakov, 2005; Roman
and Lensch, 2006).
Our approach is based on the strip mosaic, as it
has many advantages. Strip mosaic are more efficient
191
Fang S. and Campbell N. (2009).
MULTI-PERSPECTIVE PANORAMAS OF URBAN SCENES WITHOUT SAMPLING ERRORS.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 191-198
DOI: 10.5220/0001785101910198
Copyright
c
SciTePress
than view interpolation, and thus can be easily scaled
to long image sequences. Furthermore, unlike the op-
timal seam approach, even for scenes with complex
depth, strip mosaic can produce satisfactory results
by removing the sampling error and minimizing the
aspect ratio distortion. In general, we have made two
contributions:
1. We propose an approach for eliminating the sam-
pling error based on the 3D scene structure. The
principle behind our approach is similar to view
interpolation, but we only perform the “interpola-
tion” along one direction, and thus avoid the fore-
mentioned problems with the classic view inter-
polation techniques.
2. We present a two-phase optimization frame-
work to create the multi-perspective panorama.
Firstly, the optimal configuration of projections is
searched to minimize the aspect ratio distortion.
Then, local adjustment is applied to eliminate ar-
tifacts caused by undesirable perspectives.
The rest of this paper is organized as: Section 2 in-
troduces the use of strip mosaic for rendering streets
and the sampling error. Section 3 presents our ap-
proach for eliminating sampling errors. Section 4
presents the framework for generating the optimal
multi-perspective panorama. Section 5 presents the
result and Section 6 concludes this paper.
2 STRIP MOSAIC AND THE
SAMPLING ERROR
In our system, street scenes are captured by a pre-
calibrated video camera mounted on a vehicle, which
is moving down a street with a slow and smooth speed
to capture it looking sideways. Strips are cut from the
captured image sequence and pasted into the result
image. From the plan view of the capturing setup,
each strip represents a sampled ray used to render
an image from a novel horizontal projection center,
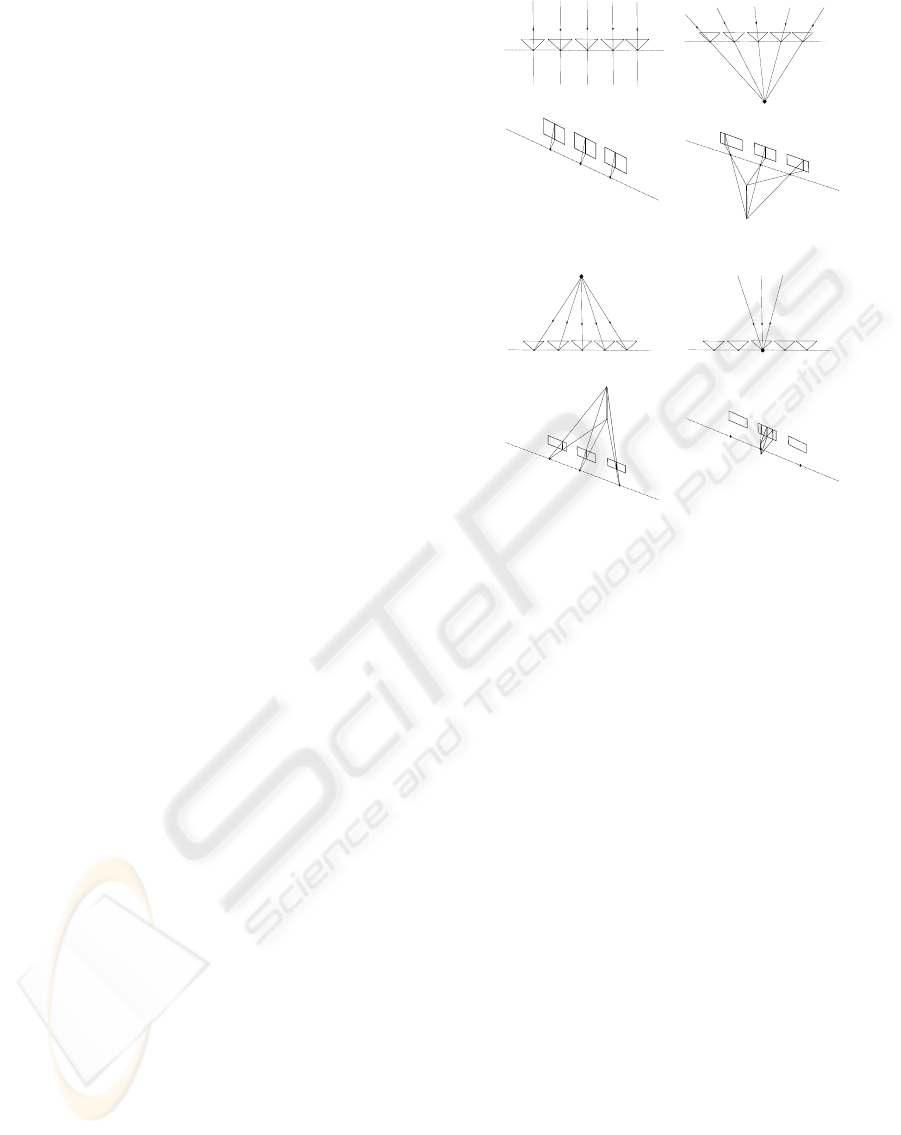
which is actually a vertical slit in the 3D view. Figure
1 illustrates projection models relevant in our applica-
tion, which are four special cases of the general linear
camera summarized in (Yu and McMillan, 2004).
Because scenes within each strip are rendered
from a particular pinhole perspective, given a cer-
tain strip width, there is a depth at which scenes
show no distortion. For a further depth, some por-
tions of the surface might be duplicately rendered,
i.e., over-sampled, while for a closer depth, some por-
tions of the surface can not be fully covered, i.e.,
under-sampled. In the literature, this kind of artifact is
named the sampling error (Zheng, 2003). Figure 2(a)
camera trajectory
camera trajectory
(a)
camera trajectory
vertical slit
vertical slit
camera trajectory
(b)
camera trajectory
vertical slit
camera trajectory
vertical slit
vertical slit
(c)
camera trajectory
vertical slit
vertical slit
camera trajectory
vertical slit
(d)
Figure 1: Projection Models. (a) The push-broom model,
where the horizontal projection center is placed at infinity.
(b) The crossed-slits model, where the horizontal projection
center is placed off the camera trajectory. (c) The inverse
perspective, where the horizontal projection center is put
behind the camera trajectory. (d) The pinhole model, where
the horizontal projection center is just placed at a camera’s
optical center.
illustrates the sampling error and Figure 2(b) gives a
real example.
3 MOSAICING WITHOUT
SAMPLING ERRORS
3.1 Single Direction Interpolation
In our system, the mosaicing result is rendered on a
picture surface, which is defined by a 3D plane π
f
.
We assume the camera trajectory lies on a plane π
c
.
If scenes are exactly located on the picture surface, a
point of the result image (p
0
, q
0
) can be mapped to a
point (p, q) of an input frame by a projective transfor-
mation, i.e., the homography:
p
q
1
= H
i
p
0
q
0
1
= P
i
G
p
0
q
0
1
(1)
where P
i
= KR
i
[I | −C
i
] is the camera matrix of the i
th
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
192

vertical slit
under-sampled
non-distortion depth
over-sampled
strip width
camera trajectory
(a)
over-sampled
under-sampled
(b)
Figure 2: The Sampling Error (a) The sampling error is
caused by the depth parallax. (b) A real example of the
sampling error.
frame. The camera parameters are extracted from the
video sequence by the structure-from-motion (SFM)
algorithm (Hartley and Zisserman, 2004). G is a 4 × 3
matrix that establishes the mappings between a 2D
point of the result image and a 3D point on the picture
surface.
We assume the horizontal projection center C
v
lies
on the camera plane and the vertical slit vl is the line
that passes through C
v
and perpendicular to the cam-
era plane. We project the camera center C
i
onto the
result image c
0
i
along the line connecting C
i
and C
v
see Figure 3. A given point of the result image is
rendered with the frame corresponding to the closest
camera center projection c
0
i
.
For scenes with complex depth structures, a pixel
from the input frame should be warped onto the result
image based on the actual 3D coordinate, which is es-
timated by an approach resembling that in (Goesele
et al., 2006). We search along the back-projected ray
of a pixel and for each depth h, we project the cor-
responding 3D coordinate onto a neighboring frame
and compute the normalized cross-correlation (NCC).
The 3D coordinate is that with the highest NCC score.
To enforce multi-view consistency, we compute the
average value of h in a set of neighboring frames and
use the robust estimation (RANSAC) to remove out-
Figure 3: The mosaic is rendered on the picture surface.
Camera centers are projected onto the picture surface and
then mapped to the final result image.
C
C
C
C
C
i
i-1
i-2
i+1
i+2
h
i, i-1
h
i, i+1
h
i, i+2
h
i, i-2
back-projected ray
inliner
outliner
Figure 4: 3D Scene coordinate reconstruction.
liers. Figure 4 illustrates the depth estimation ap-
proach.
We define a vertical center line CL
i
that passes
c
0
i
on the result image. A vertical boundary line
BL
{i↔i+1}
is drawn between any consecutive camera
center projections. The center line CL
i
is then mapped
to
c
CL
i
on the source frame I
i
. For each individual
pixel (p, q), suppose its corresponding 3D coordinate
is X
d
, its mapping onto the picture surface is the inter-
section of 3 planes: the picture surface π
f
, the plane
π
v
that contains X
d
and the vertical slit vl and the
plane π
h
that contains X
d
and the tangent line of the
camera trajectory at C
i
on the camera plane, see Fig-
ure 5. Once the intersection is recovered, it is mapped
to the result image by G
+
, the pseudo-inverse of G.
For a given input frame I
i
, we only examine pixels
within a region around
c
CL
i
. For each row of I
i
, we
take the pixel on
c
CL
i
as the starting point and search
Figure 5: A pixel from the input frame is warped to the
picture surface based on its corresponding 3D coordinate.
MULTI-PERSPECTIVE PANORAMAS OF URBAN SCENES WITHOUT SAMPLING ERRORS
193
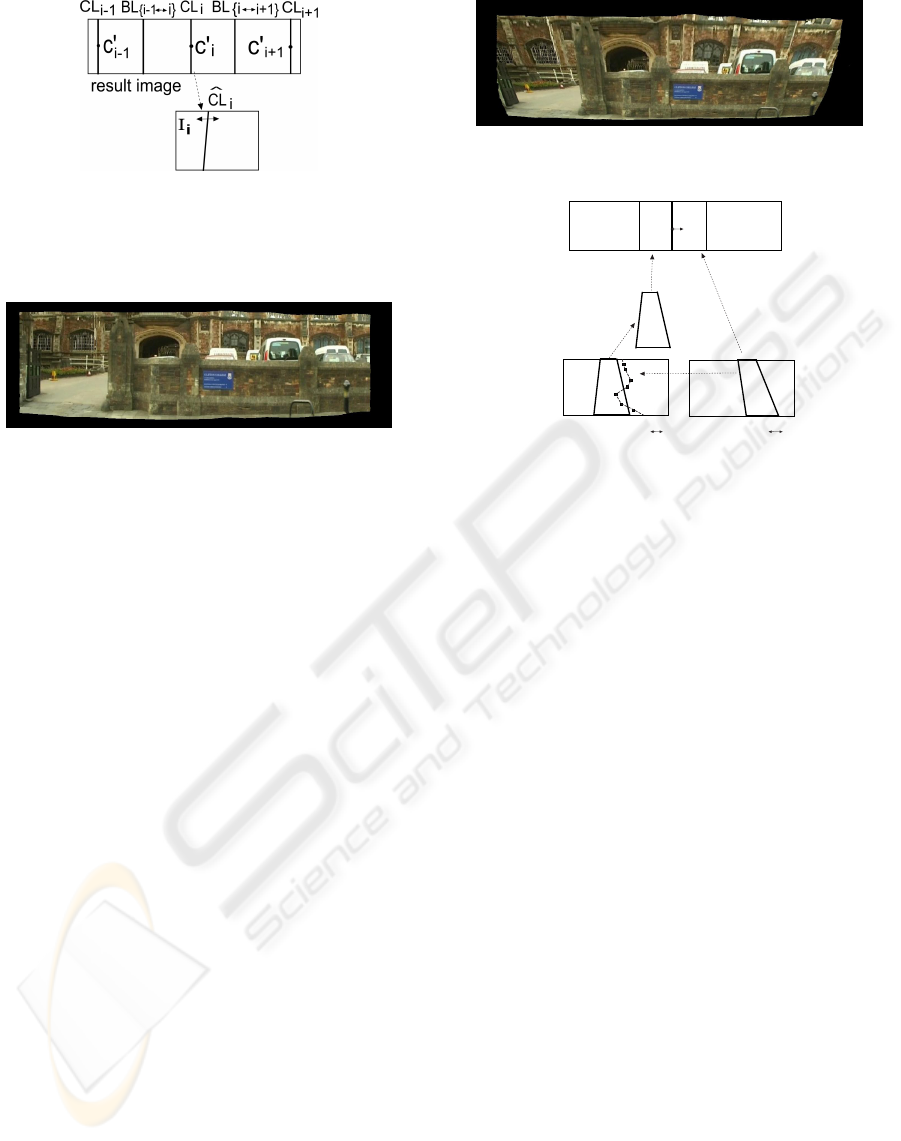
Figure 6: The center lines and boundary lines on the re-
sult image. The center line is mapped to the correspond-
ing frame. The pixel warping is carried out within a region
around the center line mapping.
Figure 7: The rendered image without sampling errors.
into both sides, once the warped point onto the re-
sult image is beyond the boundary line BL
{i↔i+1}
or
BL
{i−1↔i}
, we proceed to the next row, see Figure 6.
However, this approach is sensitive to incorrect
depth estimations. In practice, we assume the X-axis
of the camera is coincident with the tangent line of
the camera trajectory. Therefore, the value of q
0
can
be directly computed using the homograph H
i
. On the
other hand, the value of p
0
depends on the actual 3D
coordinate of (p, q). Suppose the picture surface π
f
intersects π
v
at a 3D line, and X
s
and X
t
are two points
on that 3D line, then its mapping onto the result image
is defined as:
((G
+
)
2>
X
s
)((G
+
)
3>
X
t
) − ((G
+
)
2>
X
t
)((G
+
)
3>
X
s
)
((G
+
)
3>
X
s
)((G
+
)
1>
X
t
) − ((G
+
)
3>
X
t
)((G
+
)
1>
X
s
)
((G
+
)
1>
X
s
)((G
+
)
2>
X
t
) − ((G
+
)
1>
X
t
)((G
+
)
2>
X
s
)
p
0
q
0
1
= 0
(2)
where (G
+
)
k>
denotes the k
th
row of the matrix G
+
.
By solving this equation, the value of p
0
can be de-
rived. Because with one direction the pixel warping
adopts the original projective transformation, while
the other is based on the real 3D coordinate, we name
our rendering strategy a “single direction interpola-
tion” as opposed to the full perspective interpolation.
Figure 7 shows a rendered result.
In principle, the picture surface should lie along
the dominant plane of street scenes, such as the build-
ing facet. One can fit the plane equation of the picture
surface to the 3D points discovered by the SFM al-
gorithm. However the fitting result is often a slanted
plane, which would cause an non-uniform scaling of
Figure 8: The result image is rendered on a slanted picture
surface.
CL
i
CL
i+1
BL
{ i
i+1}
CL
i
CL
i+1
BL
i+1,{ i
i+1}
BL
i,{ i
i+1}
matched points
row based warping
result image
i
i+1
^
^
^
^
H
H
I
i
I
i+1
Figure 9: The fast algorithm using depth-variant strips.
scenes, see Figure 8. Therefore, we choose the pic-
ture surface to be perpendicular to the camera plane
and parallel with the camera trajectory, i.e., fronto-
parallel. Based on this constraint, we use the least
square fit to find its plane equation.
3.2 A Fast Approximation
It is very costly to compute the actual 3D coordinate
for every warped pixel, and for large texture-less area,
the depth estimation is not reliable. Therefore, we
implement a fast approximation. Assuming
c
CL
i
and
c
CL
i+1
are mappings of the center line CL
i
and CL
i+1
,
and
c
BL
i,{i↔i+1}
and
c
BL
i+1,{i↔i+1}
are mappings of the
boundary line BL
{i↔i+1}
from the result image onto
two consecutive frames I
i
and I
i+1
, see Figure 9. We
search along the line
c
BL
i+1,{i↔i+1}
and match a set of
corresponding points on I
i
with high NCC values. By
interpolating and extrapolating these matched points,
a curved stitching line is defined on I
i
. We warp each
row based on this stitching line, then the new derived
quadrilateral is transformed to the result by H
i
. On the
other hand, the quadrilateral encompassed by
c
CL
i+1
and
c
BL
i+1,{i↔i+1}
on I
i+1
is directly transformed to
the result image by H
i+1
. The illustration is presented
in Figure 9.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
194
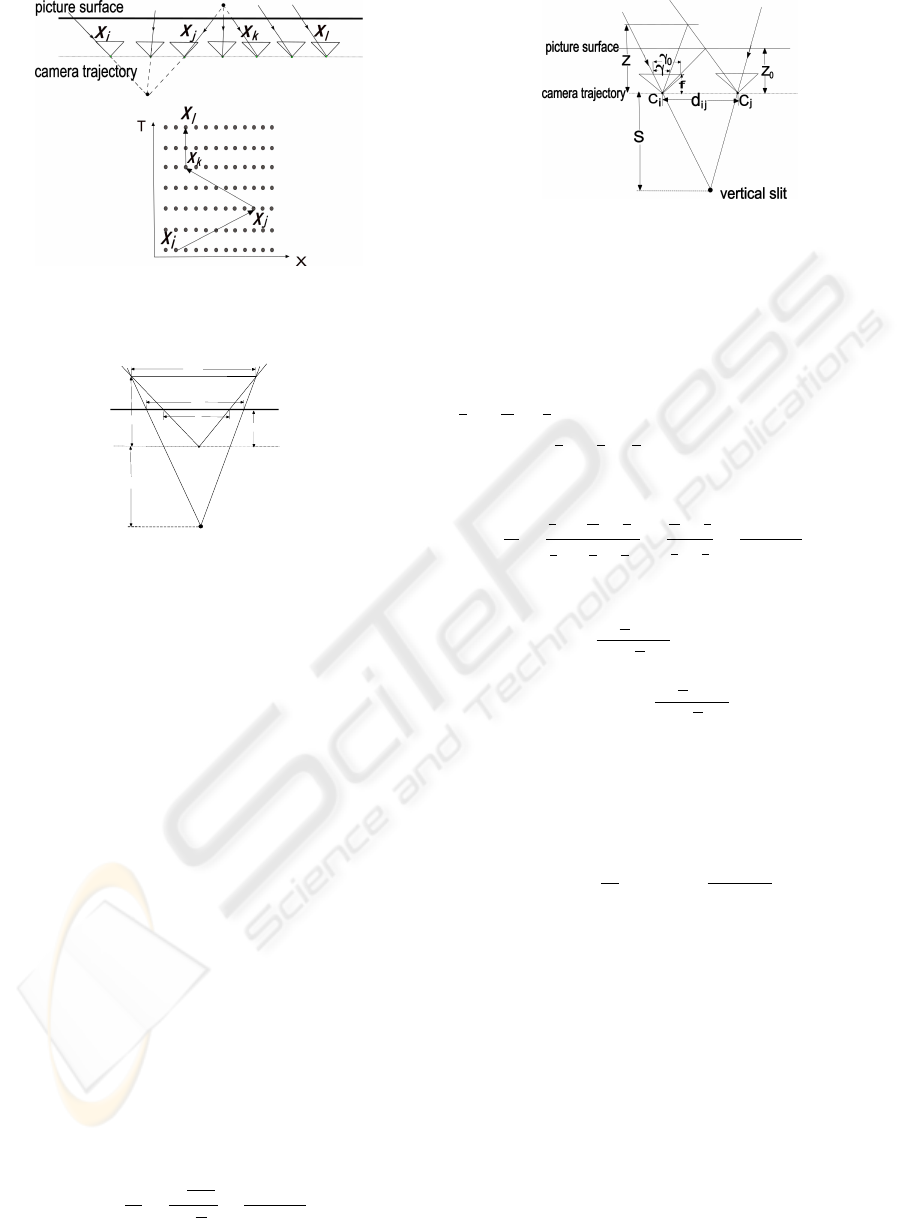
Figure 10: The multi-perspective panorama and the path on
the X-T space.
vertical slit
Z
Z
0
S
W
w
w'
C
Figure 11: The aspect ratio distortion.
4 MULTI-PERSPECTIVE
PANORAMAS
4.1 Global Optimization
This section describes how the projection models
listed in Figure 1 are automatically combined to cre-
ate a multi-perspective panorama. According to the
paradigm proposed by Wexler and Simakov (Wexler
and Simakov, 2005), the transitions of the strip loca-
tion for creating a panorama form a path through the
X-T space of the stacked volume of frames. To adopt
this paradigm, the camera trajectory is restricted to
be linear, i.e., straight. The picture surface is chosen
to be fronto-parallel. In this setup, given a particular
horizontal projection center, the center line CL
i
in the
result image is mapped to a vertical line
c
CL
i
in I
i
, so
that its X-direction location is fixed across rows. We
denote this location as x
i
. For illustration see Figure
10.
Figure 11 shows the aspect ratio distortion in this
case, defined by:
α =
w
0
w
=
W
s+z
0
s+z
W
z
0
z
=
z(z
0
+ s)
z
0
(z + s)
(3)
To search the optimal path, we need a proper cost
Figure 12: The relationship between the aspect ratio distor-
tion and strip width.
metric for strip transition. The fast approximation
algorithm gives us an intuition that the warping rate
of a row reflects the aspect ratio distortion in the re-
sult. As shown in Figure 12, if scenes are exactly
located on the picture surface the strip width γ
0
is:
1
2
d
i j
(
f
z
0
+
f
s
), while for off-plane scenes, the strip
width γ is:
1
2
d
i j
(
f
z
+
f
s
). The rate between γ
0
and γ
is equal to the aspect ratio distortion:
γ
0
γ
=
1
2
d
i j
(
f
z
0
+
f
s
)
1
2
d
i j
(
f
z
+
f
s
)
=
1
z
0
+
1
s
1
z
+
1
s
=
z(z
0
+ s)
z
0
(z + s)
= α (4)
Based on (4), we define our error metric as:
E
α
=
k
γ
0
γ
−1k
max(k
γ
0
γ
k,1)
x
i
≤ x
j
η
kx
i
−x
j
k
k
γ
0
γ
−1k
max(k
γ
0
γ
k,1)
x
i
> x
j
(5)
A backward edge (x
i
> x
j
), corresponds to an inverse
perspective, see Figure 1(c). We penalize this with
a higher cost η
kx
i
−x
j
k
, and η ≈ 1.2. Based on this
error metric, the cost function associated with a strip
transition is defined as:
E =
1
n
p
(
∑
p
E
α
) + β
kx
j
− x
i
k
d
i j
(6)
We only consider warping rates of rows with those
matched points rather than the entire strip. p denotes
such a matched point and n
p
denotes the number of
matched points involved. The second term of (6) is
used to suppress strips that are too wide, because in
this case discontinuities at strip borders are likely to
be visible. Dijkstra’s algorithm is used to find the
shortest path. After the optimal projection configu-
ration is achieved, we use the fast approximation al-
gorithm to create the sampling-error-free panorama.
We first search along the optimal path to locate all
the maximal connected forward segments and render
the result with these forward segments. Then the re-
maining backward segments are processed. Figure
13 presents an example, where some portions exhibit
MULTI-PERSPECTIVE PANORAMAS OF URBAN SCENES WITHOUT SAMPLING ERRORS
195

T
X
Forward Segment
Backward Segment
Figure 13: The result of the global optimization and the
corresponding optima path.
heavy artifacts caused by the backward segment. In
the next section, we describe how this problem can be
handled by a local adjustment step.
4.2 Local Adjustment
The idea of the local adjustment is to avoid the use
of the inverse perspective (the backward segments),
i.e., we only consider those forward segments. For
simplicity, we use the term “virtual camera” to de-
note these forward segments
1
. There are two possi-
ble spatial relationships between two adjacent virtual
cameras: their rendered areas overlap on the picture
surface Figure 14(a), or disjoint Figure 14(b). For
the latter, we need to extend the field of view of the
two virtual cameras to make them overlap, see Figure
14(c).
To make a seamless composition, we divide the
overlapping region of the two adjacent virtual cam-
eras into two parts, each of which is labeled with
pixel values from the rendered result of a single vir-
tual camera, see Figure 15. The optimal partition can
be cast into a graph cut problem. We define the cost
of a cut between any two neighboring pixels p and q
as:
C(p, q) = C
d
(p, q) + µC
g
(p, q) (7)
C
d
(p, q) is the pixel value difference and C
g
(p, q)
measures the partition cost in the gradient domain.
The weight µ is chosen to be 0.01. C
d
(p, q) is defined
1
It should be noted that the term virtual camera is only
used to denote forward segments, in fact, as shown in Fig-
ure 13, they are usually composed of several different pro-
jections.
A
start
A
end
B
start
B
end
overlapping region
(a)
A
start
A
end
B
start
B
end
empty region
(b)
A
start
A
end
B
start
B
end
overlapping region
A'
end
B'
start
(c)
Figure 14: The Spatial relationship between adjacent vir-
tual cameras. (a) Overlapping. (b) Disjoint. (c) The disjoint
virtual cameras are expanded based on the bordering pro-
jection direction.
partition line
A
start
A
end
B
start
B
end
R
A
R
B
Figure 15: The Optimal Partition.
as:
C
d
(p, q) =
∑
channel s
(NSSD(R
A
, R
B
, ω(p))+
NSSD(R
A
, R
B
, ω(q)))
(8)
where R
A
and R
B
denote the rendered images of the
two virtual cameras A and B. NSSD(R
A
, R
B
, ω(p))
is the normalized sum of squared pixel value differ-
ence between R
A
and R
B
computed in a patch around
a given pixel (ω(p)).
The gradient partition cost is the sum of two terms
measuring the gradient magnitude and similarity:
C
g
(p, q) = M
R
A
(p)+ M
R
A
(q) + M
R
B
(p)+ M
R
B
(q) +
ρ
∑
l∈{x,y}
(k∇
l
R
A
(p)− ∇
l
R
B
(p)k +
k∇
l
R
A
(q) − ∇
l
R
B
(q)k)
(9)
where M
R
A
(p) denotes the magnitude of the gradient
at a pixel, and k∇
l
· k denotes the gradient along one
dimension of the image space, x or y. We choose the
weight ρ = 0.8.
The graph cut problem is solved using the max-
flow/min-cut algorithm described in (Boykov and
Kolmogorov, 2004). Figure 16 presents the improved
panorama of Figure 13. In addition, a given portion
of the picture surface might be covered by more than
two virtual cameras. We adopt a straightforward so-
lution: virtual cameras are processed in a series and
for each incoming virtual camera, the optimal parti-
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
196

Figure 16: The multi-perspective image after local adjust-
ment. The zoom-in view shows the optimal partition line
(seam).
tion is performed on overlapping region between the
current virtual camera and areas already rendered on
the picture surface. If the incoming virtual camera has
no overlapping region with areas so far rendered, the
new virtual camera and its immediately previous one
are expanded.
5 RESULTS
We have conducted experiments on our frame-
work using image sequences captured by a digi-
tal video camcorder (Canon XM1), which captures
at 25 frames/second. Compared to existing multi-
perspective panorama generation techniques, e.g.,
(Wexler and Simakov, 2005; Roman and Lensch,
2006), the essential improvement of our approach lies
in the local adjustment as it makes our system capable
of achieving the best trade-off between the seamless
result and the maximal preservation of the human-eye
perspective. Approaches described in (Wexler and
Simakov, 2005; Roman and Lensch, 2006) are equiv-
alent to the global-optimization step in our frame-
work. In this sense, results with and without the local
adjustment shown in Figure 13 and 16 present a com-
parison between these two kinds of approaches.
We have applied our techniques to longer streets.
The result in Figure 17(a) visualizes a street that spans
around 80 meters, and the street visualized in Figure
17(b) spans around 160 meters.
For the mosaicing result in Figure 7, the cam-
era pose is extracted by Voodoo camera tracker
[http://www.digilab.uni-hannover.de/docs/manual.html]
with bundle adjustment. For long streets shown
in Figure 16, 17(a) and 17(b), we rectify the input
sequence to compensate for the camera tilt and we
assume a translational motion along the horizontal
direction at a constant speed. While, along the
(a) (b)
Figure 17: Multi-perspective panoramas. The first row of
each image set shows the partition seam and the second
without.
MULTI-PERSPECTIVE PANORAMAS OF URBAN SCENES WITHOUT SAMPLING ERRORS
197

vertical direction, the displacement is computed by
matching salient features and RANSAC is used to
remove outliers.
The optimization framework is tested on a PC
with two Xeon CPUs (2.00 GHz and 1.99 GHz) and
1.50GB ram. The global optimization of the result in
Figure 17(a) (with 980 482 × 429 input frames) takes
around 12 minutes and the result in Figure 17(b) (with
1200 395 × 227 input frames) takes around 8 minutes
2
. The local adjustment of these two results both takes
around 4 minutes.
6 CONCLUDING REMARKS
This paper presents a framework for producing multi-
perspective panoramas of street scenes. Our approach
uses an estimation of 3D scene structure to eliminate
the sampling error caused by the depth parallax. Then
an automatic optimization is performed to create the
panorama with minimal aspect ratio distortions. Af-
ter that, a further local adjustment step is applied to
remove artifacts caused by inverse perspectives. In
principle, our approach is restricted to straight cam-
era trajectories and approximately fronto-parallel pic-
ture surfaces. For non-straight camera trajectories, we
assume they are piece-wise linear. However, for tra-
jectories with abrupt direction changes, although our
rendering system can handle this situation, the result
of our global optimization is not theoretically accu-
rate, as the aspect ratio distortion in this case is not
yet clear.
REFERENCES
Agarwala, A., Agrawala, M., Cohen, M., Salesin, D., and
Szeliski, R. (2006). Photographing long scenes with
multi-viewpoint panoramas. ACM Transactions on
Graphics, 25(3):853 – 861.
Boykov, Y. and Kolmogorov, V. (2004). An experimental
comparison of min-cut/max-flow algorithms for en-
ergy minimization in vision. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 26:1124–
1137.
Chen, S. and Williams, L. (1993). View interpolation
for image synthesis. Computer Graphics, 27(Annual
Conference Series):279–288.
Davis, J. (1998). Mosaics of scenes with moving objects.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 354–360.
2
To eliminate the redundant computation of matching
points, a dense disparity map for each consecutive frame
pair is pre-computed before optimization.
Goesele, M., Curless, B., and Seitz, S. (2006). Multi-view
stereo revisited. In Proceedings of IEEE Conference
on Computer Vision and Pattern Recognition, pages
2402–2409.
Hartley, R. and Zisserman, A. (2004). Multiple view geom-
etry in computer vision. Cambridge University Press,
2 edition.
Kumar, R., Anandan, P., Irani, M., Bergen, J., and Hanna,
K. (1995). Representation of scenes from collections
of images. In Proceedings of IEEE Workshop on Rep-
resentation of Visual Scenes, pages 10–17.
Roman, A., Garg, G., and Levoy, M. (2004). Interactive
design of multi-perspective images for visualizing ur-
ban landscapes. In Proceedings of IEEE Visualization,
pages 537–544.
Roman, A. and Lensch, H. (2006). Automatic multiper-
spective images. In Proceedings of 17th Eurographics
Symposium on Rendering, pages 161–171.
Shum, H. and Szeliski, R. (2000). Construction of
panoramic image mosaics with global and local align-
ment. International Journal of Computer Vision,
36(2):101–130.
Szeliski, R. and Shum, H. (1997). Creating full view
panoramic image mosaics and environment maps. In
Proceedings of SIGGRAPH 97, Computer Graphics
Proceedings, Annual Conference Series, volume 31,
pages 251–258.
Wexler, Y. and Simakov, D. (2005). Space-time scene man-
ifolds. In Proceedings of the International Conference
on Computer Vision, volume 1, pages 858 – 863.
Yu, J. and McMillan, L. (2004). General linear cameras.
In Proceedings of European Conference on Computer
Vision, pages 14–27.
Zheng, J. (2003). Digital route panoramas. IEEE Multime-
dia, 10(3):57– 67.
Zhu, Z., Riseman, E., and Hanson, A. (2001). Parallel-
perspective stereo mosaics. In Proceedings of the
International Conference on Computer Vision, vol-
ume 1, pages 345–352.
Zomet, A., Feldman, D., Peleg, S., and Weinshall, D.
(2003). Mosaicing new views: The crossed-slits pro-
jection. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 25(6):741– 754.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
198
