
SPATIAL RECONSTRUCTION OF LOCALLY SYMMETRIC
OBJECTS BASED ON STEREO MATE IMAGES
Leonid Mestetskiy
Department of Mathematical Methods of Forecasting, Moscow State University, Moscow, Russia
Archil Tsiskaridze
Control/Management and Applied Mathematics, Moscow Institute of Physics and Technology, Moscow, Russia
Keywords: Silhouette, Stereo mate, Middle axes, Continuous skeleton, Camera calibration, Recognition of gestures,
Palm, Human body.
Abstract: Restoration of spatial objects characteristics with locally symmetric elements is proposed in this paper. An
approach based on the model of a spatial flexible object defined as a family of spheres with the centres on a
graph with a tree-like structure is proposed. A method of real time identification of such objects using the
stereo mate images of their silhouettes is introduced. Image processing comprises construction of
continuous skeletons of silhouettes. Application to real time gesture recognition is considered.
1 INTRODUCTION
Reconstruction of spatial objects using several two-
dimensional images is a well-known problem and
has many real life applications. The essence of our
approach is that two-dimensional images are
considered to be a binary image and represent only
silhouettes of a spatial object. Such statement of the
problem, in particular, arises in recognition of
gestures by means of standard inexpensive
equipment. We suppose the initial data are low
resolution (480×640) images received from standard
WEB-cameras. In 3D pose estimation of object, such
as human hand or body, texture is less important and
much of the information can be extracted from the
silhouettes alone. Recognition of a gesture requires
reconstruction of the spatial form of such a complex
and variable object as a human palm or body. The
relevance of such statement of a problem is caused
by the fact that the range of potential users of
gesture recognition systems includes a great number
of people (disabled, hard of hearing, etc.) not
capable of obtaining expensive equipment but still
deeply needing real-time gesture understanding
systems. There are works devoted to creation of deaf
alphabet understanding software (Burger and
Caplier, 2007) as well as to developing gesture-
driven computer systems (Keshkin, 2005).
The lack of texture details makes it impossible to
analyse images at texture level and apply well
known object reconstruction methods based on
automatic identification of matching points on stereo
mate images. Obviously, the boundary points are the
only points that may be reliably identified on the
silhouette images. The problem is that the boundary
points of a silhouette on one of the stereo mate
images have, as a rule, no matching points on the
boundary of the silhouette on the other image. Thus,
it is impossible to directly identify the matching
points on the stereo mate silhouette images.
One can still try to identify the matching points
making some assumptions on the nature of the
original object. As far as gesture recognition deals
with images of a human palm or body we propose to
approximately represent these objects as a union of
several "cylindrical" elements having local axial
symmetry and solve the problem using a well known
notion of a planar image skeleton. Such objects are
also called “generalised cylinders” or “tubular
objects”. To be more precise a cylindrical element is
a spatial body formed by a family of spheres with
the centres on some curve. Such objects are called
spatial fat curves. We are interested in objects that
can be represented as a union of several fat curves.
Such locally symmetric objects can be used as
models for the description of a human palm or body.
443
Mestetskiy L. and Tsiskaridze A. (2009).
SPATIAL RECONSTRUCTION OF LOCALLY SYMMETRIC OBJECTS BASED ON STEREO MATE IMAGES.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 443-448
DOI: 10.5220/0001769104430448
Copyright
c
SciTePress

It is natural that the accuracy of such description
of a human body or palm that uses generalized
cylinders is very low. Therefore, the proposed
approach cannot be used for the high-precision
reconstruction of shape and surface of 3D objects,
as, for instance, in (German Cheung Baker, 2003).
But for the recognition of gestures or poses the high
accuracy of the description of shapes and surfaces is
not required. It is sufficient to recognise only
substantial changes in the shape of these objects,
which characterise gestures. This approach makes it
possible to obtain solution of the problem with the
use of simple and inexpensive equipment under the
normal conditions.
2 THE PROPOSED METHOD
The proposed approach is based on the revealing the
of symmetry axes of the locally symmetric objects.
Although, these axes are invisible on the stereo mate
images, they still can be calculated for each image
by processing a silhouette presented on it.
We assume that the observed object does not
have occlusion. This means that all elements of the
object, for example, the fingers of a palm are visible
in the silhouette image. For objects with occlusions
it is intended to use a sequential segmentation of
initial grey scaled image to reveal overlapped parts.
Considering the silhouettes of stereo mate
images as projections of the spatial fat curves onto
the corresponding planes, we can expect that the
projections of the axes of the fat curves coincide
with the middle axes of the silhouettes.
In reality, the silhouette of a sphere is an ellipsis.
For the simplified case, when a radius of a sphere is
constant, there is a precise method of restoration
based on one silhouette image analysis
(Caglioti, 2006). For the images which we deal with,
the difference between this ellipsis and a circle is so
small, that it can be neglected.
We shall consider some (invisible) points which
are not the boundary points of the silhouettes as the
common matching points of stereo mate images.
Such reference points are provided by middle axes
of the silhouettes constituting its skeleton.
Implementation of the proposed approach poses
several problems. First we need to build the
skeletons of the silhouettes in a way that allows
identification of the points of different skeletons.
Then we have to restore the spatial form of the
whole object using the results of the identification of
the pair of skeletons. It is worth mentioning that all
calculations should be performed in the framework
of the computer vision system in real time which
requires processing of several stereo mate images
per second. This demands developing highly
efficient computational algorithms.
The notion of a flat flexible object is introduced
in (Mestetskiy, 2007) and an effective method of
comparing flexible objects on the basis of a
boundary-skeletal model is proposed. In the present
paper, we propose a generalisation of the notion of a
flat flexible object to the spatial case.
We define spatial flexible object as a set of
spheres of various sizes with centres on a spatial
tree. Stereo mate image processing allows
reconstructing the spatial structure of the object.
Reconstructing spatial characteristics of the
object allows monitoring the displacement dynamics
of the elements constituting the object, as well as the
changes in the object's shape. Applied to the human
palm or body this allows tracking their gestures or
movements.
Implementation of the proposed approach
includes solving of several subtasks.
2.1 Silhouette Acquisition
It is assumed that there is a pair of video cameras
which allows receiving synchronized images of an
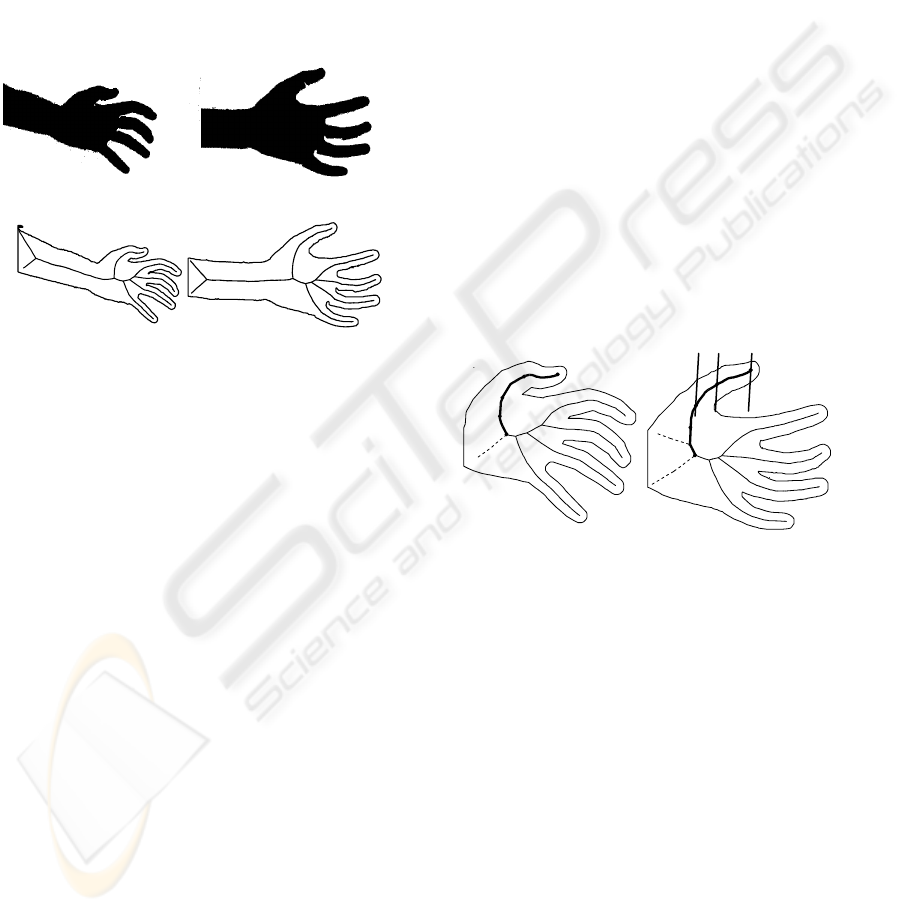
object. An example of such stereo mate images is
presented on fig.1. In our experiments the standard
web-cameras connected to the desktop computer
were used. Each image is separately segmented, then
a silhouette is extracted and represented as a binary
raster image. There are different ways of
segmentation. All of them depend on specific
applications. One can note that in gestures
recognition the requirements to the quality of
silhouette images are not very demanding. Figure 2
shows the result of palm segmentation obtained
using the background subtraction method. In this
example a simple method of background subtraction
and thresholding was used.
Figure 1: The palm stereo mate.
2.2 Continuous Skeleton
Construction of the silhouette skeletons (fig. 3) is
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
444
carried out by a method described in (Mestetskiy,
2008). A skeleton represents a geometric locus of
the centres of the circles inscribed in a silhouette.
The main advantage of the skeleton method used is
that the skeleton is represented as a graph with edges
as continuous lines. As we show later, this feature
allows successfully resolving the problem of
identification of skeleton points on different images.
Additionally, the method has the advantage of high
computing efficiency which allows solving the
problem in real time in the framework of computer
vision system.
Figure 2: The silhouettes received from two cameras.
Figure 3: Skeletons of obtained silhouettes.
2.3 Camera Calibration
Each point in the space is characterised by the
coordinates in a fixed orthogonal system which we
call a laboratory system. At the same time each
camera has its own orthogonal coordinate system,
with the centre located in the centre of the camera, z
axis is directed along the optical axis of the camera
and the two others are parallel to the coordinate axes
of the image. This camera model is called central
projection and despite its simplicity it often
constitutes an acceptable approximation to the
process of image acquisition. Camera calibration
process implies the problem of determining the
camera location in a certain laboratory coordinate
system and adjusting its internal parameters.
Another calibration method is based directly on
processing the stereo mate images, which requires
the identification of 5-8 points depending on the
method chosen (Brückner, 2008). The most
complicated part of this approach is allocation and
identification of the distinguishable points on the
images. Solving this problem with traditional
methods require a large amount of computations and
is inevitably accompanied by plenty of errors. Thus,
such approach is unacceptable when the problem
needs to be solved in real time and with the use of
web-cameras. The quality of obtained images, due to
their low resolution, does not allow reliably
detecting and identifying required number of points
on the stereo mate images. However, for locally
symmetric objects the use of skeletons makes this
problem essentially simpler. The skeleton nodes can
be used as the reference points. Thus, the problem is
reduced to identification of the nodes of two stereo
mate image skeletons.
2.4 Identification of the Reference
Points on the Skeleton
We assume that the projection of the axes of a
locally symmetric object approximately coincides
with a skeleton of the silhouette and this allows to
calculate these axes. Let
C be a point on one of the
stereo mate images. There is a straight line in the
space which is projected in this point. The image of
this straight line on the other picture is a so called
epipolar line of the point
C . For a given point on a
skeleton its stereo mate coincides with the point of
intersection of the other skeleton and the epipolar
line of this point. (fig. 4).
Figure 4: Stereo mate points found on skeletons.
2.5 Spatial Object Reconstruction
Having constructed axes on the basis of
identification of stereo mate points, it is possible to
calculate a spatial structure of a skeleton of the
object. Then, using the information on the width of
the object, with respect to the middle axes, we
restore a surface of the spatial object.
3 SKELETON POINTS
IDENTIFICATION
We describe our method of model construction for a
human palm example. We will consider stereo mate
images of a human palm (fig. 1) and the
corresponding axial graphs (fig. 4). Obviously,
fingers are locally symmetric objects. We assume
O
A
B
D
α
β
A`
B`
D`
C`
α
β
Epipolar
O`
C
SPATIAL RECONSTRUCTION OF LOCALLY SYMMETRIC OBJECTS BASED ON STEREO MATE IMAGES
445
that the projection of a spatial axis of a finger
coincides with a skeleton of a finger silhouette (fig.
4, curves
AB and
B
A
′′
).
Experiments show that the centres of the big
circles on both silhouettes (points
O and O
′
) are
the stereo mates with sufficient accuracy. Hence, it
can be assumed that the set of stereo mate points on
the sub-tree
OA
of the axial graph of the silhouette
coincides with the sub-tree
AO
′′
of the other
silhouette's axial graph. This allows constructing a
curve in the space.
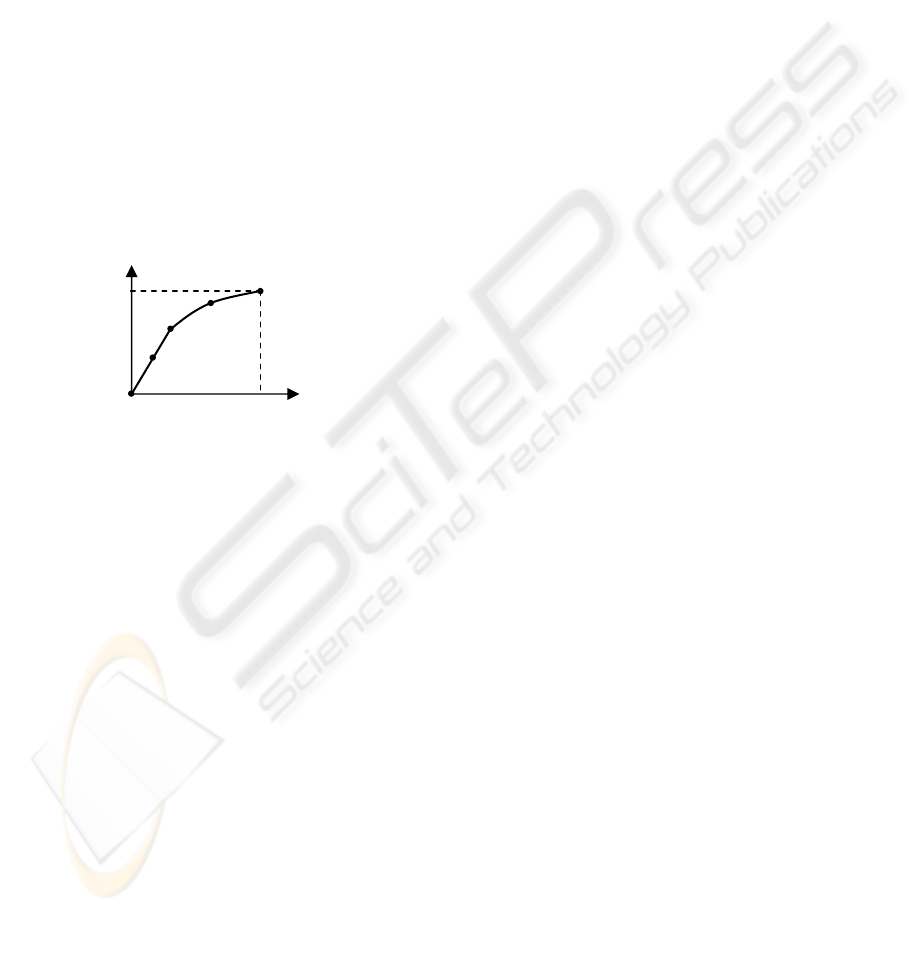
If we consider the curve
OA as a continuous
mapping
2
]1,0[: Rf →
, and the curve AO
′
′
as
2
]1,0[: Rg →
, the problem reduces to finding a
mapping
]1,0[]1,0[: →w which maps each point
)(tf into its stereo mate ))(( twg . (fig 5). Obviously,
there are restrictions imposed on
w : the mapping
should be monotonous and continuous.
Figure 5: Dependence w(t).
Let
C
be a point on one of the stereo mate
images. For a given point
)(tfC = on the curve
OA , its stereo mate
))(( twgC
=
′
is located at the
intersection of the curve
AO
′′
and the epipolar of
C . Thus, using the epipolar lines, it is possible to
identify the stereo mate points on axial graphs and
determine the spatial arrangement of the axes of the
fat lines.
However, the difficulty arises when the
intersection angel
)(t
θ
of the curve
AO
′
′
and the
epipolar line is small, and therefore
C
′
is defined
with great inaccuracy. We can avoid this, by
imposing the following restriction
mi
n
)(
θθ
>t . The
value of
w(t) can be calculated only if
min
θ>θ(t) . In order to determine w(t) when
min
θθ(t) ≤ we interpolate using already obtained
values of
w . The application of the linear
interpolation is quite comprehensible to our
problem.
In figure 5, restriction
mi
n
θθ(t) > is violated on
curve
OB
, thus this curve is a segment.
Based on identification of the skeleton points we
obtain complete spatial configuration of the axes of
the given locally symmetric object. In many cases,
this representation is enough to handle the problems
of gesture recognition. However, the method of
skeletal representation contains not only the
information on the mid-axes of an object, but also
the information on the width of an object, since the
radii of inscribed circles with the centres on the mid-
axes are known. This information on the width of
the object makes it possible to visualise a
constructed spatial model.
4 VISUALIZATION
Having constructed spatial axes and calculated the
sizes of spheres with the centres on these axes, we
can reconstruct a spatial image of the object. For
each point
γ
of the spatial axial graph we define a
corresponding sphere in the following way: let
Q
be a point of the axial graph of one of the silhouettes
which is the image of
γ
. There exists a
corresponding maximal sized circle S with the centre
in
Q which is inscribed in the silhouette. The given
circle is the image of a sphere
r
S with the centre in
γ
and radius
r
. Let's choose an arbitrary point
),(, vuPSP
=
∈
. It determines a ray l which
starts in the centre of the first camera and is tangent
to the sphere
r
S . Then
r
is a distance between the
point
γ
and the ray l .
Thus, the sphere radius can be calculated. The
model of the object is a surface enveloping the set of
these spheres. An example of a human palm model
visualization obtained from the stereo mate images
is presented on fig. 6.
One can see from this example that the
visualization is not quite realistic, since in the model
not only the fingers are described as the fat curves,
but also a palm part between the fingers and a wrist
is considered as a fat curve. This fault of
visualization can be easily eliminated because the
spatial position of the fingers makes it possible to
calculate the plane where this palm part is located
and slightly flatten the sphere towards this plane.
The result of such an improvement is presented on
fig. (7).
(1, 1)
t
(0, 0)
A
C
B
D
w(t)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
446
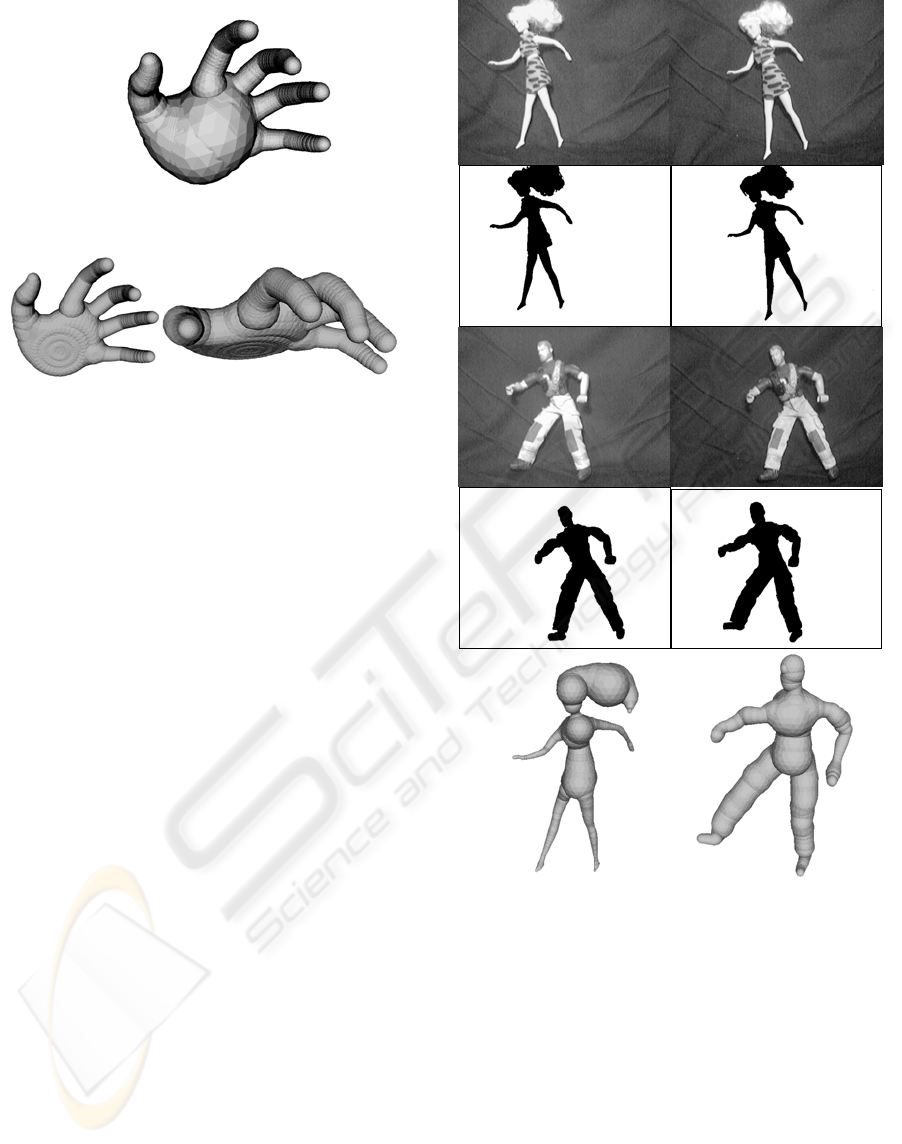
Figure 6: Spatial model visualization.
Figure 7: Corrected spatial model.
5 EXPERIMENTAL RESULTS
Experiments with the reconstruction of the spatial
model of a human body were conducted with dolls
of a size of 30 cm. The only purpose of using the
dolls was to simplify the process of taking photos in
the laboratory conditions. The results can easily be
extrapolated for a case of a real human body. Figure
7 shows the initial stereo mate images, their
silhouettes and the resulting spatial objects.
The experimental estimation of the accuracy of
restoration of human body shape can be obtained
with the use of "Kung-Fu Girl" data, presented by
Graphics-Optics-Vision group at the Max-Planck
Institute for Informatics (MPII). These data consist
of synthetic scenes (size 240×320) obtained from the
virtual cameras, for which the precise values of the
calibration parameters are known. The results of the
experiments are shown on figure 9. Visual analysis
shows that the accuracy of restoration of body shape
and surface is very poor. But, this accuracy looks
like completely sufficient for restoring poses and
gestures. We intend to investigate the formal
quantitative criterion of accuracy and the methods
for its calculation.
The performance of the algorithm implemented
on Intel Pentium IV, Core 2 Duo, 2800 Mhz, 1Gb
RAM computer is more than 5 frames per second.
This makes it possible to use the proposed method as
a real time tool in the framework of the computer
vision systems.
Figure 8: Stereo mate of initial images, their silhouettes
and the received spatial objects.
SPATIAL RECONSTRUCTION OF LOCALLY SYMMETRIC OBJECTS BASED ON STEREO MATE IMAGES
447

Figure 9: Stereo mate of initial images and received spatial
objects for “Kungfu girl”.
ACKNOWLEDGEMENTS
Authors are grateful to the Russian Foundation of
Basic Researches, which has supported this work
(grant 05-01-00542).
REFERENCES
Mestetskiy, L., 2007. Shape comparison of flexible objects
-similarity of palm silhouettes.
International
conference on computer vision theory and
applications. (VISAPP 2007)
, Volume IFP/IA,
Barcelona, Spain, 2007, p.390-393.
Mestetskiy, L., Semenov, A., 2008. Binary image skeleton
- continuous approach.
International conference on
computer vision theory and applications (VISAPP
2008)
, Volume 1, Funchal, Madeira, Portugal, 2008,
p.251-258.
Caglioti, V., Giusti A., 2006. Reconstruction of canal
surfaces from single images under exact perspective.
European Conference on Computer Vision.
German, K.M., Cheung, S., Baker and T. Kanade. Visual
Hull Alignment and Refinement Across Time: A 3D
Reconstruction Algorithm Combining Shape-From-
Silhouette with Stereo,
in Proceedings of IEEE
Conference on Computer Vision and Pattern
Recognition 2003 (CVPR'03)
, Vol. 2, pages 375-382
Forsyth, A., Ponce, J., 2003.
Computer Vision: A Modern
Approach
, Prentice Hall
Burger, T., Caplier, A., Mancini, S., 2007, Cued speech
hand gestures recognition tool.
International
Conference on Computer Vision Theory and
Applications
.
Keskin, C., Aran, O., Akarun, L., 2005. Real time gestural
interface for generic applications.
European Signal
Processing Conference
, EUSIPCO 2005.
Brückner, M., Bajramovic, F., Denzler, J., 2008.
Experimental evaluation of relative pose estimation
algorithms.
International Conference on Computer
Vision Theory and Applications
.
Hartley, R., Zisserman, A., 2004.
Multiple View Geometry
in Computer Vision
. Cambridge University Press, 2
nd
edition
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
448
