
SEMI-SUPERVISED DISTANCE METRIC LEARNING FOR VISUAL
OBJECT CLASSIFICATION
Hakan Cevikalp
Eskisehir Osmangazi University, Eskisehir, Turkey
Roberto Paredes
Universidad Politecnica de Valencia, Valencia, Spain
Keywords:
Dimensionality reduction, Image segmentation, Metric learning, Pairwise constraints, Semi-supervised learn-
ing, Visual object classification.
Abstract:
This paper describes a semi-supervised distance metric learning algorithm which uses pairwise equivalence
(similarity and dissimilarity) constraints to discover the desired groups within high-dimensional data. As op-
posed to the traditional full rank distance metric learning algorithms, the proposed method can learn nonsquare
projection matrices that yield low rank distance metrics. This brings additional benefits such as visualization
of data samples and reducing the storage cost, and it is more robust to overfitting since the number of esti-
mated parameters is greatly reduced. Our method works in both the input and kernel induced-feature space,
and the distance metric is found by a gradient descent procedure that involves an eigen-decomposition in each
step. Experimental results on high-dimensional visual object classification problems show that the computed
distance metric improves the performance of the subsequent clustering algorithm.
1 INTRODUCTION
Learning distance metrics is very important for var-
ious vision applications such as object classification,
image retrieval, and video retrieval (Chen et al., 2005;
Cevikalp et al., 2008; Hertz et al., 2003; Hadsell
et al., 2006), and this task is much easier when the
target values (labels) associated to the data samples
are available. However, in many vision applications,
there is a lack of labeled data since obtaining labels
is a costly procedure as it often requires human effort.
On the other hand, in some applications, side informa-
tion - given in the form of pairwise equivalence (sim-
ilarity and dissimilarity) constraints between points -
is available without or with less extra cost. For in-
stance, faces extracted from successive video frames
in roughly the same location can be assumed to repre-
sent the same person, whereas faces extracted in dif-
ferent locations in the same frame cannot be the same
person. Side information may also come from human
feedback, often at a substantially lower cost than ex-
plicit labeled data. Our motivation in this study is that
using side information effectively in metric learning
can bridge the semantic gaps between the low-level
image feature representations and high-level semantic
concepts in many visual applications, which enables
us to select our preferred characteristics for distinc-
tion. A typical example is organizing image galleries
in accordance to the personal preferences. For exam-
ple, one may want to group the images as outdoors or
indoors. Similarly, we may want to group face images
by race or gender. In most of these cases, typical dis-
tance functions employed in vision community such
as Euclidean distance or Gaussian kernels do not give
satisfactory results.
Recently, learning distance metrics from side in-
formation has been actively studied in machine learn-
ing. Existing distance metric learning methods re-
vise the original distance metric to accommodate the
pairwise equivalence constraints and then a cluster-
ing algorithm with the learned distance metric is
used to partition data to discover the desired groups
within data. In (Xing et al., 2003), a full pseudo
distance metric, which is parameterized by positive
semi-definite matrices, is learned by means of convex
programming using side information. The metric is
learned via an iterative procedure that involves projec-
tion and eigen-decomposition in each step. Relevant
Component analysis (RCA) (Bar-Hillel et al., 2003) is
introduced as an alternative to this method. But it can
315
Cevikalp H. and Paredes R. (2009).
SEMI-SUPERVISED DISTANCE METRIC LEARNING FOR VISUAL OBJECT CLASSIFICATION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 315-322
DOI: 10.5220/0001768903150322
Copyright
c
SciTePress

exploit only similarity constraints. (Kwok and Tsang,
2003) formulate a metric learning problem that uses
side information in a quadratic optimization scheme.
Using the kernel trick, the method is also extended
to the nonlinear case. Although the authors claim
that the learned metric is a pseudo-metric, there is no
guarantee that the resulting distance metric yields a
positive semi-definite matrix. (Shalev-Shwartz et al.,
2004) proposed a sophisticated online distance met-
ric learning algorithm that uses side information. The
method incorporates the large margin concept and the
distance metric is modified based on two successive
projections involving an eigen-decompsoition. Note
that all semi-supervised distance metric learning algo-
rithms mentioned above attempt to learn full rank dis-
tance metrics. In addition to these methods, there are
some hybrid algorithms that unify clustering and met-
ric learning into a unique framework (Bilenko et al.,
2004).
In this paper we are interested in semi-supervised
visual object classification problems. In these tasks,
the quality of the results heavily relies on the cho-
sen image representations and the distance metric
used to compare data samples. The imagery data
samples are typically represented by pixel intensi-
ties, multi-dimensional multi-resolution histograms
or more sophisticated “bag-of-features” based repre-
sentations using patch-based shape, texture and color
features. Unfortunately, these representations usu-
ally tend to be high-dimensional and most of the dis-
tance metric learning techniques fail in these situa-
tions. This is due to the fact that most dimensions
in high-dimensional spaces do not carry information
about class labels. Furthermore, learning an effec-
tive full rank distance metric by using side informa-
tion cannot be carried out in such high-dimensional
spaces since the number of parameters to be estimated
is related to the square of the dimensionality and there
is insufficient side information to obtain accurate es-
timates (Cevikalp et al., 2008). A typical solution
to this problem is to project the data onto a lower-
dimensional space and then learn a suitable metric
in the resulting low-dimensional space. There is a
large number of dimensionality reduction methods in
the literature (Goldberger et al., 2004; Globerson and
Roweis, 2005; Torresani and Lee, 2006; Turk and
Pentland, 1991). But most of them cannot be used
in our case since they are supervised methods that re-
quire explicit class labels. On the other hand, relying
on an unsupervised dimensionality reduction method
is also problematic since important discriminatory in-
formation may be lost during a completely unsuper-
vised dimensionality reduction. A better approach
would be to use a semi-supervised dimensionality re-
duction method to find a low-dimensional embedding
satisfying the pairwise equivalence constraints as in
(Cevikalp et al., 2008). In this paper we propose such
an algorithm that works in both the input and kernel
induced-feature space. In contrast to the traditional
full rank distance metric learning methods, the pro-
posed method allows us to learn nonsquare projec-
tion matrices that yield low rank pseudo metrics. This
brings additional benefits such as visualization of data
samples and reducing the storage cost and it is more
robust to overfitting since the number of estimated pa-
rameters is greatly reduced. The proposed method
bears similarity to the semi-supervised dimension re-
duction method introduced in (Cevikalp et al., 2008),
but it does not assume that samples in a sufficiently
small neighborhood tend to have same label. Instead
we focus on improving the local margin (separation).
The remainder of the paper is organized as fol-
lows: In Section 2, we introduce the proposed method
and extend it to the nonlinear case. Section 3 de-
scribes the data sets and experimental results. Finally,
we present conclusions in Section 4.
2 METHOD
2.1 Problem Setting
Let x
i
∈ IR
d
, i = 1,...,n, denote the samples in the
training set. We are given a set of equivalence con-
straints in the form of similar and dissimilar pairs. Let
S be the set of similar pairs
S =
(x
i
,x
j
)|x
i
and x
j
belong to the same class
and let D be the set of dissimilar pairs
D =
(x
i
,x
j
)|x
i
and x
j
belong to different classes
.
Assuming consistency of the constraints, the con-
straint sets can be augmented using transitivity and
entailment properties as in (Basu et al., 2004).
Our objective is to find a pseudo-metric that satis-
fies the equivalence constraints and at the same time
reflects the true underlying relationships imposed by
such constraints. We focus on pseudo-metrics of the
form
d
A
(x
i
,x
j
) = ||x
i
− x
j
||
A
=
q
(x
i
− x
j
)
>
A(x
i
− x
j
),
(1)
where A ≥ 0 is a symmetric positive semi-definite
matrix. In this case there exists a rectangular pro-
jection matrix W of size q × d (q ≤ d) satisfying
A = W
>
W such that
||x
i
− x
j
||
2
A
= ||Wx
i
− Wx
j
||
2
. (2)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
316

From this point of view the distance between two
points under metric A can be interpreted as linear pro-
jection of the samples by W followed by Euclidean
distance in the projected space. As a result, optimiz-
ing with respect to W rather than A allows us to re-
duce the dimensionality of the data and find low rank
distance metrics. In the following, we will first show
how to find a (potentially) full rank distance metric
A using side information and then extend the idea to
allow low rank metrics.
2.2 Learning Full Rank Distance
Metrics
Intuitively, the learned distance metric must pull sim-
ilar pairs closer and push the dissimilar pairs apart.
Additionally, it should generalize well to unseen data.
To this end, we minimize the following differentiable
cost function defined based on sigmoids
J(A) =
1
N
∑
i, j∈S
1
1 + exp[−β(||x
i
− x
j
||
2
A
−t
s
)]
+
1
M
∑
i, j∈D
1
1 + exp[β(||x
i
− x
j
||
2
A
−t
d
)]
, (3)
where N is the number of similar pairs, M is the num-
ber of dissimilar pairs, β is a design parameter that
controls the slope of the sigmoid functions, and t
s
and
t
d
are the selected thresholds. This cost function has
two competing terms as illustrated in Fig. 1. The first
term encourages pulling similar points closer, and the
second term penalizes small distances between dis-
similar pairs. The dissimilar pairs which are closer to
each other contribute more to the loss function than
the ones which are further from each other for well
chosen β (In fact if the dissimilar pairs are too far
from each other they do not contribute to the los func-
tion at all). Therefore, just as in the Support Vector
Machine’s hinge loss, the second term of the above
loss function is only triggered by dissimilar pairs in
the vicinity of decision boundary which participate in
shaping the inter-class decision boundaries. From a
dimensionality reduction point of view, this can be
thought as paying more attention to the displacement
vectors between the dissimilar pairs where classes ap-
proach each other since these are good candidates for
discriminant directions preserving inter-class separa-
bility. Although recent supervised distance learning
techniques take the margin concept into consideration
during learning (Torresani and Lee, 2006; Weinberger
et al., 2005), this issue is largely ignored in semi-
supervised distance metric learning methods (Kwok
and Tsang, 2003; Xing et al., 2003).
It should be noted that we need at least one active
dissimilar sample pair (the closer dissimilar samples
(a) (b)
Figure 1: Visualization of sigmoidal functions used in op-
timization. The first function (a) handles similar pairs, and
it takes higher values as the distances between similar pairs
increase. The second function (b) is used with dissimilar
pairs and it takes higher values if the distances between dis-
similar pairs are smaller than the selected threshold.
contributing to the lost function) since simply min-
imizing the above loss function over the set of all
similar pairs leads to a trivial solution. Therefore in-
cluding dissimilar pairs is crucial in our method
1
.We
would like to find a positive semi-definite distance
matrix that minimizes the above criterion. To do so,
we can apply a gradient descent based approach. Let
u = (x
i
−x
j
)
>
A(x
i
−x
j
) and dx
i j
= (x
i
−x
j
). Differ-
entiating J(A) with respect to the distance matrix A
gives the following gradient for the update rule
∂J(A)
∂A
=
1
N
∑
i, j∈S
βexp[−β(u −t
s
)]
(1 + exp[−β(u −t
s
)])
2
dx
i j
dx
>
i j
−
1
M
∑
i, j∈D
βexp[β(u −t
d
)]
(1 + exp[β(u −t
d
)])
2
dx
i j
dx
>
i j
. (4)
To optimize the cost function we iteratively take a
small step in the direction of the negative of this gra-
dient. However, this updating rule does not guaran-
tee positive semi-definiteness on matrix A. To do
so, the matrix A must be projected onto the positive
semi-definite cone at each iteration. This projection is
performed by taking the eigen-decomposition of the
computed distance matrix and removing the compo-
nents with negative eigenvalues if exist any. At the
end, the resulting distance matrix is shaped mostly
by the displacement vectors between closer dissimilar
pairs and the displacement vectors between far-away
similar pairs. The algorithm is summarized below:
Initialization. Initialize A
0
to some positive defi-
nite matrix.
Iterate. Do the following steps until convergence:
1
If the dissimilarity information is not available, we
need an additional constraint such as
∑
i, j
|A
i j
| > 0 in or-
der to avoid a trivial solution. But, we will not consider
this case here since dissimilarity information is available in
most applications.
SEMI-SUPERVISED DISTANCE METRIC LEARNING FOR VISUAL OBJECT CLASSIFICATION
317

• Set
e
A
t+1
= A
t
− η
∂J(A)
∂A
.
• Apply eigen-decomposition to
e
A
t+1
and recon-
struct it using positive eigenvalues and corre-
sponding eigenvectors A
t+1
=
∑
k
λ
k
e
k
e
>
k
.
2.3 Learning Low Rank Distance
Metrics
As we mentioned earlier, distance between two sam-
ples under positive semi-definite distance matrix A
can be interpreted as linear projection of the samples
followed by Euclidean distance in the projected space,
i.e., d
A
(x
i
−x
j
) = ||Wx
i
−Wx
j
||. Therefore low rank
distance metrics satisfying equivalence constraints
also allow low-dimensional projections which reduce
the dimensionality of the original input space. Re-
ducing the dimensionality offers several advantages:
First, projection of samples onto a lower-dimensional
space reduces the storage requirements. Secondly,
projections onto 2 or 3-dimensional space allow us
visualization of data, so we can devise an interactive
constraint selection tool and verify the effects of our
selections visually.
Unfortunately, optimization of J(A) subject to
rank-constraints on A is not convex and difficult to
solve (Globerson and Roweis, 2005; Torresani and
Lee, 2006). One way to obtain a low rank distance
matrix is to solve for full rank matrix A using the al-
gorithm described earlier, and then obtain a low rank
projection by using its leading eigevalues and corre-
sponding eigenvectors as in (Globerson and Roweis,
2005). A more elaborate way to obtain low rank dis-
tance matrix is to formulate the optimization problem
with respect to nonsingular projection matrix W of
size q×d rather than A. Here q ≤ d represents the de-
sired rank of the distance matrix. This formulation is
more efficient and robust to overfitting since the num-
ber of unknown parameters (elements of W) is sig-
nificantly reduced. The rank of the resulting distance
matrix A is at most q since the equation A = W
>
W
holds and the projected samples Wx
i
lie in IR
q
.
Our original cost function can be written in terms
of W as
J(W) =
1
N
∑
i, j∈S
1
1 + exp[−β(||Wx
i
− Wx
j
||
2
−t
s
)]
+
1
M
∑
i, j∈D
1
1 + exp[β(||Wx
i
− Wx
j
||
2
−t
d
)]
, (5)
Now let u = (x
i
− x
j
)
>
W
>
W(x
i
− x
j
). If we differ-
entiate J(W) with respect to W, we obtain
∂J(W)
∂W
=
2W
N
∑
i, j∈S
βexp[−β(u −t
s
)]
(1 + exp[−β(u −t
s
)])
2
dx
i j
dx
>
i j
−
2W
M
∑
i, j∈D
βexp[β(u −t
d
)]
(1 + exp[β(u −t
d
)])
2
dx
i j
dx
>
i j
. (6)
As in the first case we have to ensure that the re-
sulting distance matrix is positive semi-definite. To
this end, we construct A from W and apply eigen-
decomposition on A. This computation can be effi-
ciently done by performing a thin singular value de-
composition on W instead of performing a full eigen-
decomposition on A. After removing the negative
eigenvalues and corresponding eigenvectors we re-
construct the projection matrix as
W = Λ
1/2
E, (7)
where Λ is a diagonal matrix of nonzero eigenvalues
of positive semi-definite matrix A, and E is the matrix
whose columns are the corresponding eigenvectors.
The algorithm is summarized as follows:
Initialization. Initialize W
0
to some rectangular
matrix such that W
>
0
W
0
is positive semi-definite.
Iterate. Do the following steps until convergence:
• Set
f
W
t+1
= W
t
− η
∂J(W)
∂W
.
• Construct
e
A
t+1
=
f
W
t+1
f
W
>
t+1
and apply eigen-
decomposition to
e
A
t+1
and reconstruct it using
positive eigenvalues and corresponding eigenvec-
tors
e
A
t+1
=
∑
k
λ
k
e
k
e
>
k
.
• Reconstruct the projection matrix as W
t+1
=
Λ
1/2
t+1
E
t+1
.
3 EXTENSIONS TO NONLINEAR
CASES
Here we consider the case where the data samples are
mapped into a higher-dimensional feature space and
the distance metric is sought in this space. We re-
strict our analysis to nonlinear mappings φ : IR
d
→
F where the dot products in the mapped space can
be obtained by using a kernel function such that <
φ(x
i
),φ(x
j
) >= k(x
i
,x
j
) for some kernel k(.,.).
Let Φ = [φ(x
1
) ... φ(x
n
)] denote the matrix whose
columns are the mapped samples in F . We define
k
x
= Φ
>
φ(x) = [k(x
i
,x]
n
i=1
as n×1 kernel vector of x
against training samples. As in Kernel Principal Com-
ponents Analysis (Scholkopf et al., 1998), we con-
sider parametrizations of W of the form W = ΩΦ
>
,
where Ω ∈ IR
q×n
is some matrix allowing to write W
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
318

as a linear combinations of the mapped samples. In
this setting, the distance matrix A can be written as
A = W
>
W = ΦΩ
>
ΩΦ
>
. (8)
By defining the positive semi-definite matrix as
b
A =
Ω
>
Ω, the original problem can be converted into
looking for a positive semi-definite matrix
b
A since the
distance in the mapped space under the distance ma-
trix A can be written as
(k
x
i
− k
x
j
)
>
b
A(k
x
i
− k
x
j
) =
ˆ
dx
i j
>
ΦΩ
>
ΩΦ
>
ˆ
dx
i j
,
(9)
where
ˆ
dx
i j
= φ(x
i
) − φ(x
j
). As can be seen in the
equation above, the distance between two samples
in the mapped space depends only on dot products
which are computed in the original input space. This
is equivalent to transformation of the input data into n-
dimensional feature space through Φ
>
φ(x
i
) followed
by the distance metric learning in the transformed
space. Thus, by using the proposed algorithms de-
scribed earlier, we can search a full rank matrix
b
A
or low-dimensional projection matrix Ω in the trans-
formed kernel feature space.
Nonlinear distance metric learning is not very use-
ful for visual object classification tasks since the orig-
inal input space is already high-dimensional. But, it
may be useful for some other applications where the
input space is typically low-dimensional and finding
a distance metric satisfying all pairwise equivalence
constraints is not be feasible, e.g., exclusive-or prob-
lem.
4 EXPERIMENTS
We perform experiments on three different computer
vision applications and attempt to discover the de-
sired unknown groups in these. The proposed Semi-
Supervised Distance Metric Learning (SSDML) al-
gorithm is compared to the full rank distance metric
learning algorithm followed by dimensionality reduc-
tion and the Constrained Locality Preserving Projec-
tion (CLPP) method of (Cevikalp et al., 2008). The
k-means and spectral clustering methods are used as
clustering algorithm with the learned distance metric,
and pairwise F-measure is used to evaluate the cluster-
ing results based on the underlying classes. The pair-
wise F-measure is the harmonic mean of the pairwise
precision and recall measures. To demonstrate the
effect of using different number of equivalence con-
straints, we gradually increased the number of simi-
lar and dissimilar pairs. In all visual object classifi-
cation experiments, constraints are uniformly random
selected from all possible constraints induced by the
true data labels of the training data, and clustering per-
formance is measured using only the test data. We
used the same value for both thresholds t
s
and t
d
, and
it is chosen to be 0.1µ
S
, where µ
S
is the averages of
distances between similar pairs under the initial dis-
tance metric.
4.1 Experiments on Gender Database
Here we demonstrate how the proposed method can
be used to organize image galleries in accordance to
the personal preferences. In these applications we de-
termine a characteristic for distinction and group im-
ages based on this selection. In our case we group
images by gender and use the gender recognition
database used in (Villegas and Paredes, 2008). This
database consist of 1892 images (946 males and 946
females) coming from the following databases: AR,
BANCA, Caltech Frontal face, Essex Collection of
Facial Images, FERET, FRGC version 2, Georgia
Tech and XM2VTS. Only the first frontal image of
each individual was taken, however because all of the
databases have more male subjects than females, the
same number of images is taken for both male and
female subjects. All images are cropped based on
the eye coordinates and resized to 32 × 40 yielding
a 1280-dimensional input space. Then, images are
converted to gray-scale followed by histogram equal-
ization. Some samples are shown in Fig. 2.
Figure 2: Some male and female samples from Gender
database.
We used 50% of the images as training data and
the remaining for testing. The dimensionality d =
1280 of the input space is too high, thus we learned
a projection matrix of size 10 × d yielding a low rank
distance matrix. Since we cannot directly apply the
other full rank distance metric learning techniques
in this high-dimensional space, we first applied di-
mensionality reduction methods, Principal Compo-
nent analysis (PCA) and Locality Preserving Pro-
jections (LPP) (He and Niyogi, 2003), to the high-
dimensional data, and learned a distance metric in the
reduced space. The size of the reduced space is cho-
sen such that 99% of the overall energy (sum of the
eigenvalues) is retained. To learn the distance met-
ric in the reduced space, we used the method pro-
SEMI-SUPERVISED DISTANCE METRIC LEARNING FOR VISUAL OBJECT CLASSIFICATION
319
50
55
60
65
70
75
80
0 100 200 300 400 500 600 700 800
F-Measure
Number of Constraints
SSDML
PCA+MetricLearning
LPP+MetricLearning
CLPP
50
55
60
65
70
75
80
0 100 200 300 400 500 600 700 800
F-Measure
Number of Constraints
SSDML
PCA+MetricLearning
LPP+MetricLearning
CLPP
(a) (b)
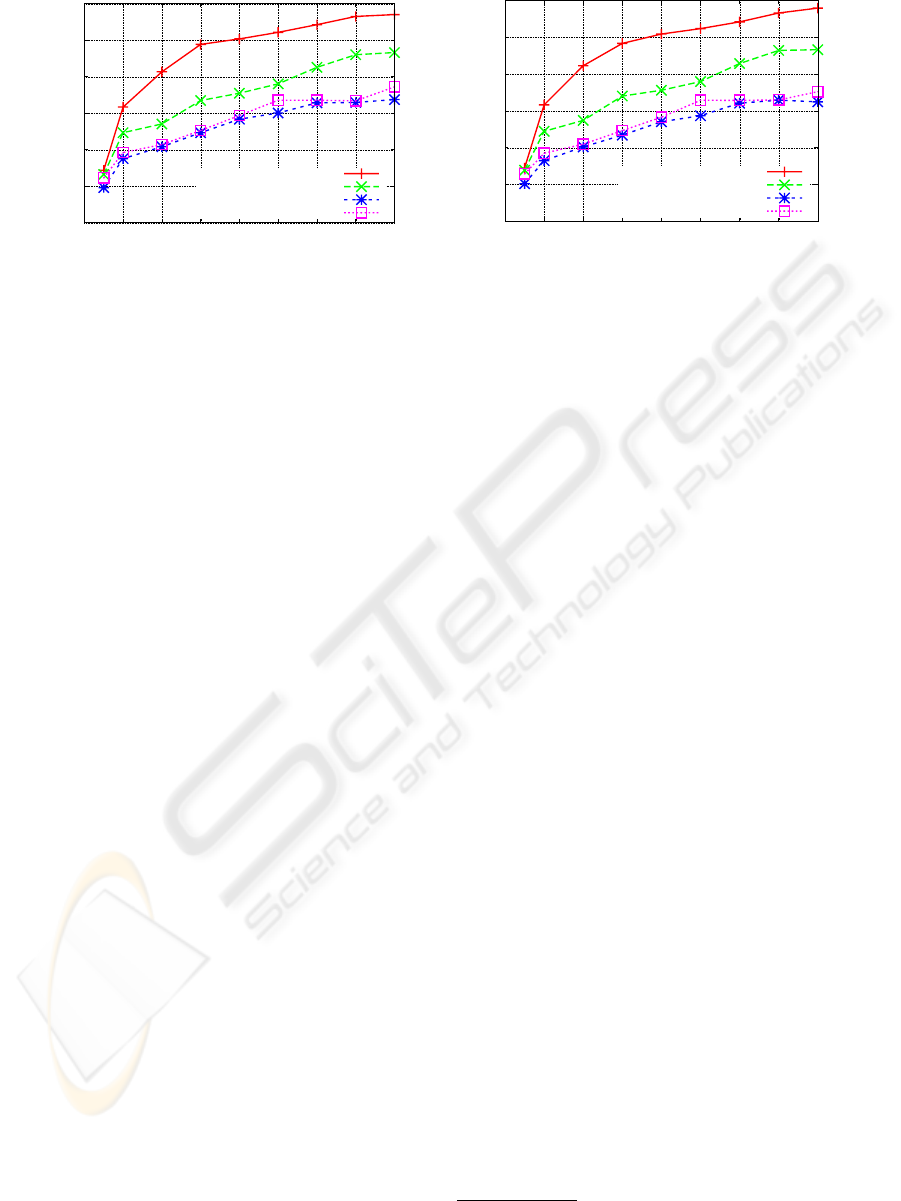
Figure 3: F-measure as a function of number of constraints for (a) k-means clustering, (b) spectral clustering on Gender
database.
posed in (Kwok and Tsang, 2003). The reported
clustering performances are averages over 10 random
test/training splits.
Clustering accuracies as a function of constraints
are shown in Fig. 3. As can be seen, the proposed
method outperforms competing methods for both k-
means and spectral clustering in all cases. PCA fol-
lowed by the distance metric learning comes the sec-
ond and LPP followed by the distance metric learn-
ing performs the worst. CLPP method yields simi-
lar accuracies to LPP followed by the distance met-
ric learning. The poor performance of CLPP suggests
that the samples coming from male and female sub-
jects in small neighborhoods do not have the same la-
bel. Both clustering algorihtms, k-means and spectral
clustering, yield similar results.
4.2 Experiments on Birds Database
The Birds database (Lazebnik et al., 2005) contains
six categories, each having 100 images. It is a chal-
lenging database since the birds appear against highly
cluttered backgrounds and images have large intra-
class, scale, and viewpoint variability. We used a “bag
of features” representation for the images as they are
too diverse to allow simple geometric alignment of
their objects. In this method, patches are sampled
from the image at many different positions and scales,
either densely, randomly or based on the output of
some kind of salient region detector. Here we used a
dense grid of patches. Each patch was described using
the robust visual descriptor SIFT assignment against
a 2000 word visual dictionary learned from the com-
plete set of training patches. The dimensionality of
the input space is still high, thus we learned a non-
square projection matrix with rank 10 and we reduced
the dimensionality before applying the full distance
metric learning technique as in the first experiment.
We used 50% of the images as training data and re-
maining for testing. Results are again averages over
10 random test/training splits.
Results are shown in Fig. 4. Initially, PCA fol-
lowed by the full rank distance metric learning per-
forms better than the proposed method. As the num-
ber of the constraints increases, the proposed method
takes the lead and outperforms competing methods.
CLPP comes the second and LPP followed by the dis-
tance metric learning again performs the worst. This
time, k-means clustering yields better results than
spectral clustering.
4.3 Image Segmentation Applications
We also tested proposed method on image segmen-
tation applications where the dimensionality of the
sample space is relatively small compared to the vi-
sual object classification problems. We experimented
with images chosen from the Berkeley Segmentation
dataset
2
. Centered at every pixel in each image we ex-
tracted a 20 ×20 pixel image patch for which we com-
puted the robust hue descriptor of (van de Weijer and
Schmid, 2006). This process yields a 36-dimensional
feature vector which is a histogram over hue values
observed in the patch, where each observed hue value
is weighted by its saturation. We compared our pro-
posed method to the image segmentation based on
Normalized Cuts (NCuts) (Shi and Malik, 2000). The
Heat kernel function using Euclidean distance is used
as kernel in NCuts segmentation. As in (Cevikalp
et al., 2008), we set the number of clusters to two, one
cluster for the background and another for the object
of interest.
The pairwise equivalence constraints are chosen
2
Available at http://www.eecs.berkeley.edu/
Research/Projects/CS/vision/grouping/segbench/
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
320
35
40
45
50
55
60
65
70
75
100 200 300 400 500 600 700 800 900
F-Measure
Number of Constraints
SSDML
PCA+MetricLearning
LPP+MetricLearning
CLPP
30
35
40
45
50
55
60
65
70
100 200 300 400 500 600 700 800 900
F-Measure
Number of Constraints
SSDML
PCA+MetricLearning
LPP+MetricLearning
CLPP
(a) (b)
Figure 4: F-measure as a function of number of constraints for (a) k-means clustering, (b) spectral clustering on Birds database.
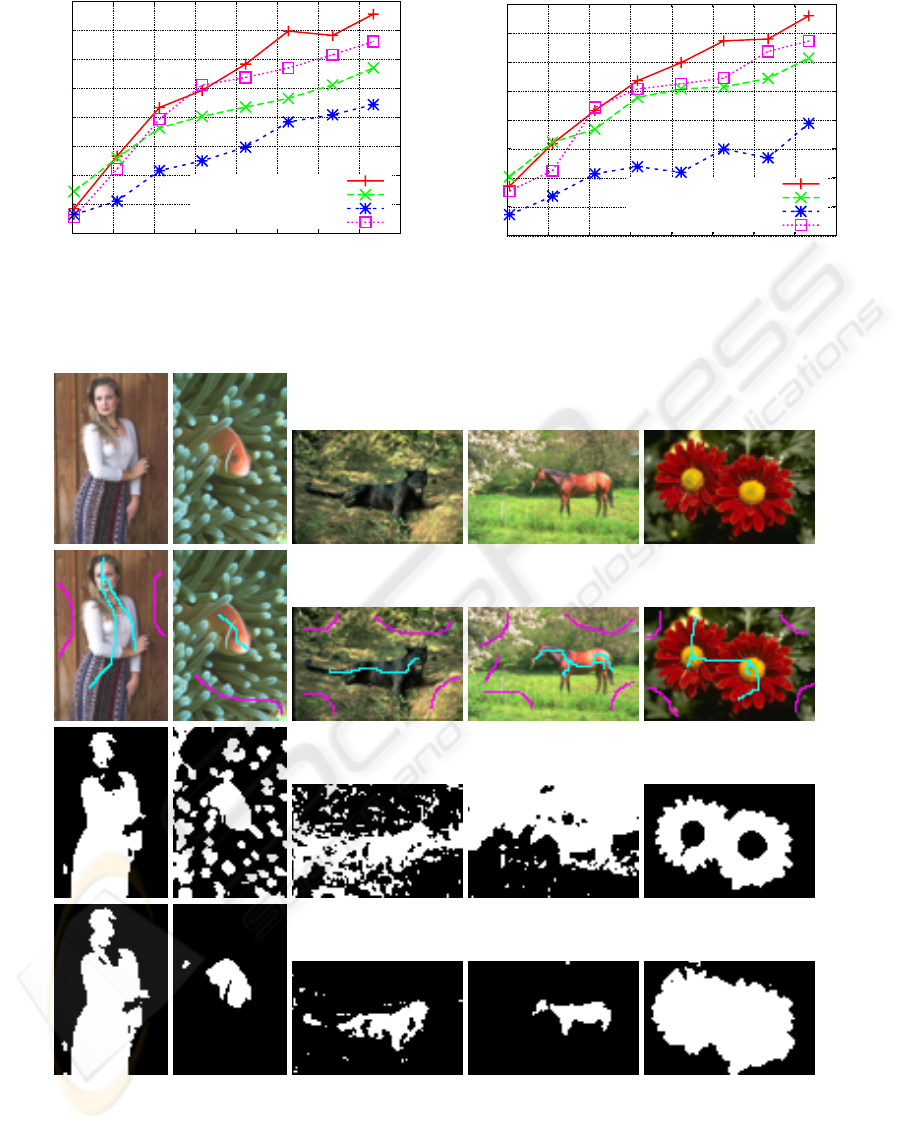
Figure 5: Original images (top row), pixels used for equivalence constraints (second row), segmentation results without
constraints (third row), and segmentation results using constraints (bottom row). Figure is best viewed in color.
from the samples corresponding to pixels shown with
magenta and cyan in the second row of Fig. 5. We
first segmented the original images without any su-
pervision using NCuts algorithm. Then, we used the
proposed method with the selected constraints to learn
a projection matrix W with rank 10 and then used
SEMI-SUPERVISED DISTANCE METRIC LEARNING FOR VISUAL OBJECT CLASSIFICATION
321

NCuts segmentation in the learned space. As can be
seen in the figures, simple used added equivalence
constraints can improve the segmentations.
5 SUMMARY AND
CONCLUSIONS
In this paper we proposed a semi-supervised distance
metric learning method, which uses pairwise equiv-
alence constraints to discover the desired groups in
high-dimensional data. The method works in both
the input and kernel induced-feature space and it
can learn nonsquare projection matrices that yield
low rank distance metrics. The optimization proce-
dure involves minimizing two terms defined based on
sigmoids. The first term encourages pulling simi-
lar sample pairs closer while the second term max-
imizes the local margin. The solution is found by
a gradient descent procedure that involves an eigen-
decomposition.
Experimental results show that the proposed
method increases performance of subsequent cluster-
ing and classification algorithms. Moreover, it yields
better results than methods applying unsupervised di-
mensionality reduction followed by full rank metric
learning.
ACKNOWLEDGEMENTS
Roberto Paredes is supported by the grant from Span-
ish project TIN2008-04571.
REFERENCES
Bar-Hillel, A., Hertz, T., Shental, N., and Weinshall, D.
(2003). Learning distance functions using equivalence
relations. In International Conference on Machine
Learning.
Basu, S., Banerjee, A., and Mooney, R. J. (2004). Active
semi-supervision for pairwise constrained clustering.
In the SIAM International Conference on Data Min-
ing.
Bilenko, M., Basu, S., and Mooney, R. J. (2004). Integrat-
ing constraints and metric learning in semi-supervised
clustering. In the 21st International Conference on
Machine Learning.
Cevikalp, H., Verbeek, J., Jurie, F., and Klaser, A. (2008).
Semi-supervised dimensionality reduction using pair-
wise equivalence constraints. In Computer Vision The-
ory and Applications.
Chen, H. T., Liu, T. L., and Fuh, C. S. (2005). Learning ef-
fective image metrics from few pairwise examples. In
IEEE International Conference on Computer Vision.
Globerson, A. and Roweis, S. (2005). Metric learning by
collapsing classes. In Advances in Neural Information
Processing Systems.
Goldberger, J., Roweis, S., Hinton, G., and Salakhutdinov,
R. (2004). Neighbourhood component analysis. In
Advances in Neural Information Processing Systems.
Hadsell, R., Chopra, S., and LeCun, Y. (2006). Dimension-
ality reduction by learning and invariant mapping. In
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition.
He, X. and Niyogi, P. (2003). Locality preserving direc-
tions. In Advances in Neural Information Processing
Systems.
Hertz, T., Shental, N., Bar-Hillel, A., and Weinshall, D.
(2003). Enhancing image and video retrieval: Learn-
ing via equivalence constraints. In IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition.
Kwok, J. T. and Tsang, I. W. (2003). Learning with ideal-
ized kernels. In International Conference on Machine
Learning.
Lazebnik, S., Schmid, C., and Ponce, J. (2005). A max-
imum entropy framework for part-based texture and
objcect recognition. In International Conference on
Computer Vision (ICCV).
Scholkopf, B., Smola, A. J., and Muller, K. R. (1998). Non-
linear component analysis as a kernel eigenvalue prob-
lem. Neural Computation, 10:1299–1319.
Shalev-Shwartz, S., Singer, Y., and Ng, A. Y. (2004). Online
and batch learning of pseudo metrics. In International
Conference on Machine Learning.
Shi, J. and Malik, J. (2000). Normalized cuts and image
segmentation. IEEE Transactions on PAMI, 22:885–
905.
Torresani, L. and Lee, K. C. (2006). Large margin com-
ponent analysis. In Advances in Neural Information
Processing Systems.
Turk, M. and Pentland, A. P. (1991). Eigenfaces for recog-
nition. Journal of Cognitive Neuroscience, 3:71–86.
van de Weijer, J. and Schmid, C. (2006). Coloring local fea-
ture extraction. In European Conference on Computer
Vision (ECCV).
Villegas, M. and Paredes, R. (2008). Simultaneous learn-
ing of a discriminative projection and prototype for
nearest-neighbor classification. In IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition.
Weinberger, K. Q., Blitzer, J., and Saul, L. K. (2005). Dis-
tance metric learning for large margin nearest neigh-
bor classification. In Advances in Neural Information
Processing Systems.
Xing, E. P., Ng, A. Y., Jordan, M. I., and Russell, S. (2003).
Distance metric learning with application to clustering
with side-information. In Advances in Neural Infor-
mation Processing Systems.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
322
