CACHED MULTI-BOUNCE SOLUTION AND RECONSTRUCTION
FOR VOXEL-BASED GLOBAL ILLUMINATION
Łukasz Piwowar
Institute of Computer Science, University of Wrocław, Poland
R
´
emy Malgouyres
∗
Univ. Clermont 1, LAIC, EA2146, IUT Campus des C
´
ezeaux, BP 86 63172 Aubi
`
ere cedex, France
Keywords:
Realistic Rendering, Global Illumination, Voxel, Reconstruction, Multi-bounce.
Abstract:
We address the main shortcomings of the voxel-based multi-bounce global illumination method of Chatelier
and Malgouyres (2006), by introducing an iterated cached method which allows increasing sampling coarse-
ness at each bounce for improved efficiency, and by introducing a ray-tracing based reconstruction process for
a better final image quality. The result is a competitive accurate multi-bounce global illumination method with
octree voxel-based irradiance caching.
1 INTRODUCTION
Comprehensive multi-bounce methods for global il-
lumination have been extensively studied, and find-
ing the right balance of speed vs accuracy is always
painful. The most widely used approach consists in
one step of coarse computation of a global illumi-
nation solution followed by a step of reconstruction
by gathering the light by ray-tracing to provide good
quality images.
In (Malgouyres, 2002) and (Chatelier and Malgo-
uyres, 2006), a new to global illumination and a dis-
cretization of the diffuse illumination, based on voxel
approximation of surfaces by voxels is proposed. The
interest of the method is that visibility is determined
in linear time with respect to the number of rays.
Moreover, it directly provides a voxel-based irradi-
ance lookup octree. However, the method presented
in (Chatelier and Malgouyres, 2006) has two weak-
nesses: first, solid angle sampling is the same for each
bounce, and in particular, direction sampling from
light sources is insufficient while the cost of direc-
tion sampling after one or two bounces is very expen-
sive. Second, no reconstruction process is presented
and direct display of the voxel solution requires many
voxels, which also increases the runtime.
∗
This work was supported by the French National Re-
search Agency under contract GEODIB ANR-06-BLAN-
0225
In this paper, we address these two shortcomings
by proposing an iterated cached coarse global illu-
mination solution, in which direction sampling de-
creases after each bounce, followed by a reconstruc-
tion phase based on light cuts (Walter et al., 2005). It
results in a competitive accurate multi-bounce global
illumination method with a voxel irradiance cache oc-
tree.
In section 2, we have presented previous work
and outline the method of (Chatelier and Malgouyres,
2006). In Section 3, we present the iterated cached
global illumination method, and in Section 4, we ex-
plain our reconstruction process. In Section 5, we
present experimental results. Finally, in Section 6 we
present some perspectives for future works.
2 PREVIOUS WORK
The most widely used global illumination techniques
consist in a first phase of computation of a coarse
solution, for example by photon mapping (Jensen,
1996), (Jensen, 1997), (Jensen, 2001). This method
traces random rays from light sources, and at each
intersection, traces a new random ray with a prob-
ability that depends on the BRDF according to rus-
sian roulette. Then, a second phase consists in a
viewpoint-dependant ray-tracing for computing good
173
Piwowar Ł. and Malgouyres R. (2009).
CACHED MULTI-BOUNCE SOLUTION AND RECONSTRUCTION FOR VOXEL-BASED GLOBAL ILLUMINATION.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 173-178
DOI: 10.5220/0001768301730178
Copyright
c
 SciTePress

quality images. Instant radiosity ((Keller, 1997)) was
the first of such methods to be introduced. Other
methods for final gather steps have been produced
(Granier and Drettakis, 2004), (Arikan et al., 2005).
In all of these methods, determining visibility by
ray-object intersection is a very important time cost
factor. Attempts at getting rid of visibility problems
altogether have been made (Dachsbacher et al., 2007),
however at a cost of increased memory and reintro-
ducing hierarchical radiosity difficult problems of re-
finement and meshing (Sillion and Puech, 1994). For
accelerating the gather step, photon splatting (Lav-
ignotte and Paulin, 2003), (Dachsbacher and Stam-
minger, 2006) can by used, but it neglects some occlu-
sions for indirect light and uses rough approximations
for speedup.
In (Chatelier and Malgouyres, 2006), a new global
illumination approach is considered, with a cost
which is linear with respect to the number of visibility
rays. This is a promising result, but there are short-
comings. The goal of this paper is to provide solution
to these, to obtain a competitive global illumination
technique. Up to the end of this section, we outline
the method of (Chatelier and Malgouyres, 2006).
In (Malgouyres, 2002), the (Lambertian) global il-
lumination equation
B(x) = E(x) + ρ(x)
Z
S
B(y)
cos θ
π
d
−→
σ
is discretized as
B(x) = E(x) +ρ(x)
∑
−→
σ ∈D
B(I(x,
−→
σ ))
cosθ(x,I(x,
−→
σ ))
π
∆Ω(
−→
σ )
where x is now a voxel, D is a set of discrete di-
rections in space, I(x,
−→
σ ) is the first point y viewed
from x in the direction of
−→
σ (as in a ray-object
intersection), and ∆Ω(
−→
σ ) is the fraction of a solid
angle associated to the direction
−→
σ . In (Chatelier
and Malgouyres, 2006), a solution of the discrete
equation is obtained with a linear complexity with
respect to the number of rays. We remind the reader
the main ideas of the method. More details can be
found in (Chatelier and Malgouyres, 2006).
Given a direction vector (a,b,c) ∈ Z
3
with a ≥
b ≥ c, a notion of a 3D line has been proposed
(Debled-Rennesson, 1995), as the set of points
(x,y,z) ∈ Z
3
such that
µ ≤ cx − az < µ + ω and µ
0
≤ bx − ay < µ
0
+ ω
0
where µ,µ
0
,ω,ω
0
are integers. Other cases can be
deduced by symmetry. Let us denote by Z
3
∗
the set
Z
3
\{(0,0,0)}. Given an integer vector
−→
v ∈ Z
3
∗
, the
set Z
3
can be partitioned into 3D discrete lines, whose
direction vector is
−→
v (see Figure 1).
Figure 1: Partition of the space into parallel discrete lines.
Moreover, given a voxel x ∈ Z
3
, finding out which
3D discrete line in the partition the point x belongs to
can be done in constant time.
Now, to transfer energy from one voxel x to the
first voxel y visible from x in a direction σ, for some
finite set of sample directions σ, if we consider some
fixed direction σ and a partition of the voxel space
Z
3
into discrete lines parallel to σ, then the voxels of
the discretized surface (say mesh or implicit surface)
that lie on the same discrete line can be arranged in
an ordered list. In this ordered list, the first visible
voxel is the next voxel in the list. So, once the lists
are sorted, we can propagate the energy in linear time
O(N), where N is the number of voxels.
Now, the idea of the method is that by going over
the set of all surface voxels in a lexicographic order
(lexicographic orders are precomputed by radix sort),
we can build all the sorted lists in linear time O(N).
We do this for each of the D sample directions and
for each of the I Gauss-Seidel iteration, and we get a
numerical solution of the global illumination equation
in time O(N × I × D).
3 SHOOTING FROM LIGHT
SOURCES AND BOUNCE
CACHE METHOD
Although the method of (Chatelier and Malgouyres,
2006) has a linear complexity with respect to the num-
ber of rays, one of its drawbacks is that it doesn’t sam-
ple solid angles according to power importance. We
consider small light sources which emit much light
per unit of area, as we can find in many applications,
first the voxel size needs to be small enough to ap-
proximate light source shapes, thus many voxels are
required, and second, the solid angle sampling must
be fine enough to avoid artifacts. A natural solution
to this problem is the use of the raytracing instead of
discrete shooting in this step. We proceed as follows:
First we choose number of initial photons on light
sources with the random normal distribution that de-
pends on light power and area. The energy of each
sample is equal to
overall energy
number of samples
. Then we shoot
from each initial photon n rays into n directions, with
energy equal to E/n. For each intersection point we
store the given energy and compute the correspond-
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
174

(a) Direct photons shooting (b) Initial voxel power
Figure 2: Photons shooting and voxels initialization.
ing irradiance. The set of indirect photons is used as
initial voxel setup (the initial voxel irradiance is equal
to the sum of the irradiance of the photons inside the
voxel). We propagate this light using the linear voxel
method of (Chatelier and Malgouyres, 2006).
After each bounce of Lambertian surface, the en-
ergy amount is reduced significantly, and is getting
lower frequency (i.e. more smooth). We can use that
property by using less directions at each intersection
level, thus reducing the cost of multi-bounce simula-
tion. At each bounce we propagate only the light that
was created during previous shooting phase, summing
all the light in a global accumulation cache after each
iteration. We split computations into sets of indepen-
dent i to i + 1 bounces, and we use different (e.g. di-
vided by 2 at each bounce) number of directions at
each level. The algorithm can be sketched as follows:
• We shoot photons from light sources by raytracing
at path length one (only first intersections).
• We sum the irradiance in the corresponding vox-
els and use the result as initialization of the linear
method of (Chatelier and Malgouyres, 2006). We
store this in currentCache.
• for each iteration
we propagate currentCache and store new
values into CachePlus
we add the energy from CachePlus to
GlobalCache
we swap CachePlus and currentCache
we clear CachePlus
4 RECONSTRUCTION METHOD
We present two approaches to light gathering for
voxel-based global illumination: one similar to in-
stant radiosity (Keller, 1997) and one based on light-
cuts (Walter et al., 2005).
4.1 Random Sample Voxels
Our first reconstruction is inspired from instant ra-
diosity (Keller, 1997). Of course, the principle must
be substantially adapted to voxels. The intensity of
the voxels is proportional to their radiosity as ob-
tained in the output of the method of (Chatelier and
Malgouyres, 2006) improved by the iterated cached
method. However, in order to reduce the number of
point lights, and to take into account the nature of ra-
diosity (power per unit of steradian per unit of area)
we select the voxels randomly according to a proba-
bility proportional to their area, as defined below, and
multiplied by a solid angle.
The area of a voxel is the sum for all boundary
voxel of an object of the dot product of the normal to
the faces of the voxel with the normal to the underly-
ing surface.
∆A(x) =
∑
y∈N
6
(x)∩O
−→
xy.
−→
N (1)
So, we make a raytracing phase by tracing rays
from the viewpoint through the pixels. For each pixel,
we compute the ray hit point I that we must shade. In
order to shade the hit point I, we use the sample vox-
els y, randomly selected with probability proportional
to ∆A(y), as point light sources with light contribu-
tion:
C
y
(I) = B(y)
cos θ(I,y)cos θ(y,I)
||I − y||
2
V (I,y) (2)
In fact, we select two random samples sets of vox-
els by monte-carlo sampling. We can use progres-
sive raytracing that allows the user to get approximate
results after a few seconds. This method generated
nice images, but its complexity is dependent on O(n)
where n is number of virtual point lights.
4.2 Reconstruction based on Lightcuts
In order to reduce the dominant reconstruction cost,
we use the lightcuts method (Walter et al., 2005). This
method enables us to render massive (thousands to
millions) number of point lights in a reasonable (sub-
linear) time. The only drawback is a small pixel po-
tential error value (determined by a user-set param-
eter, e.g. 2%) . A cluster is a set of point light
sources which are approximated by a single represen-
tative light source. A common lightcut tree, the nodes
of which are clusters, is created which unifies illumi-
nation and enables transparent tradeoffs between ade-
quate components. During the reconstruction process,
at a ray hit point, the largest clusters compatible with
CACHED MULTI-BOUNCE SOLUTION AND RECONSTRUCTION FOR VOXEL-BASED GLOBAL
ILLUMINATION
175

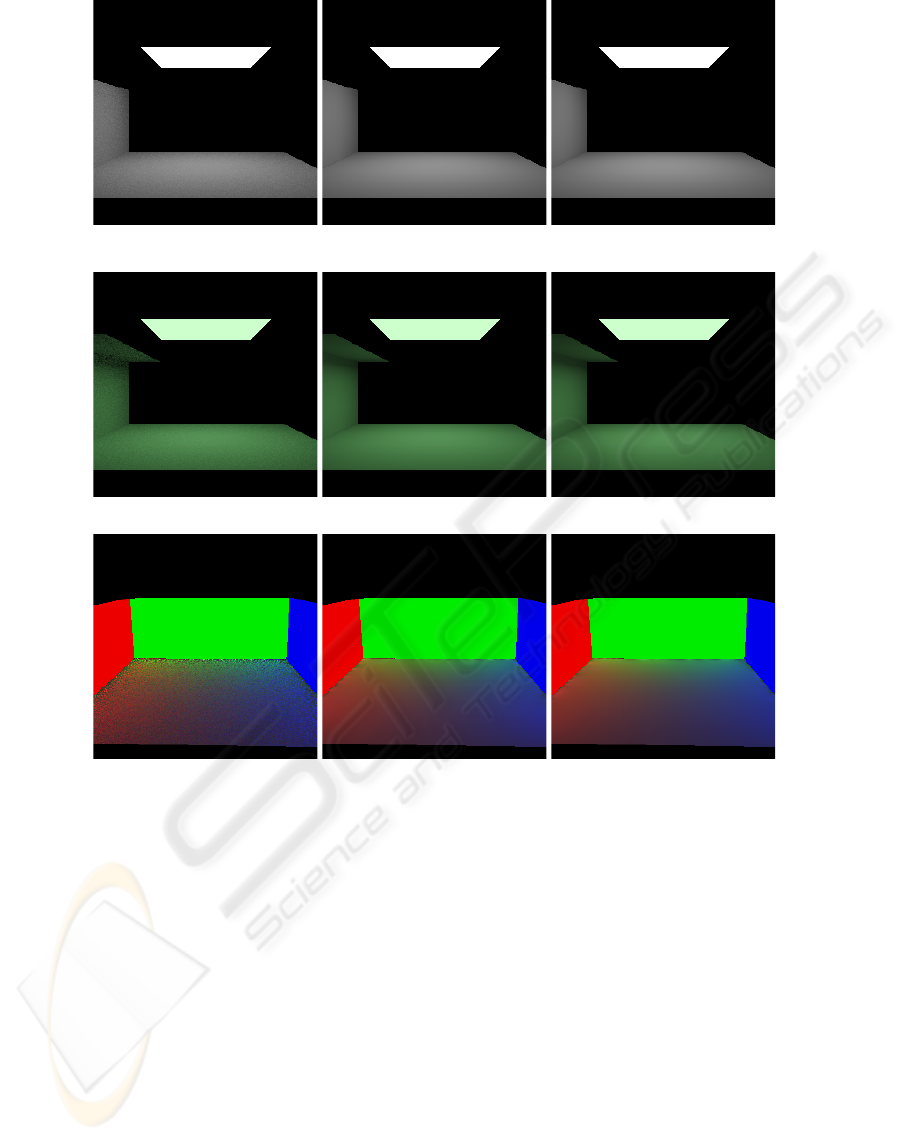
(a) 13.5 sec (b) 11.2 sec (c) 9.0 sec
(d) 14.3 sec (e) 13.1 sec (f) 11.5 sec
(g) 18.0 sec (h) 20.6 sec (i) 21.0 sec
Figure 3: Comparison tests. the left column was computed by monte carlo path tracing (50 samples per pixel), the middle
column is photon mapping with lightcuts for reconstruction, and the right column is the voxel-based method with lightcut
reconstruction. All pictures were computed using 1600 direct photons. We used 1600 indirect photons for photon mapping.
We used 128 directions in the linear voxel propagation, and 2 iterations. The discretization resolution was 64 ×64×64 voxels.
the error criterion is selected, and summed to obtain
the irradiance value. This method allows us, instead
of using a random sample of voxels, to consider all the
voxels. This simplifies the voxel selection process, at
a cost of constructing lightcuts trees.
Our implementation of lightcuts is based on (Mik-
sik, 2007). We divide direct and indirect virtual light
points and create separate trees, and combine them
in a root node as described in (Miksik, 2007). The
direct tree is based on light source photons and the
first irradiance cache (for direct light) of the method
of Section 3. The indirect tree is based on the indirect
accumulation voxel cache.
5 RESULTS
Tests were done on PC with Intel Core 2 Duo 6300
(1.86GHz). Only one core was used (single thread
with Widows Vista).
The first test compares the method with a refer-
ence solution computed by path tracing. In Figure 3,
a quality comparison with other classical methods is
provided. The results shows that the method is accu-
rate and without noise. We computed path-tracing at
a constant rate samples per pixel (50) thus the time
is sometimes better, but the noise is strongly visible.
This test shows that the method is accurate.
In Table 1, we can see the statistics for runtime.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
176

Table 1: Statistics for Scene 1.
Scene 1 Scene 2
Antialiasing off on
number of triangles 1,176 67,462
number of voxels 108,455 22,615
Light path length 4 6
Voxel directions 146 256
Primary photons 650 4000
Direct photons 200 256
Continuous Rays 87,913,202 184,834,570
Discrete Rays 26,637,785 10,146,637
Rays/sec (continuous) 140,819 68,983
Rays/sec (discrete) 5,122,651 5,176,855
Propagation Time 6.1 sec 4.15 sec
Linear method Time 5.2 sec 1.96 sec
Reconstruction Time 624.3 sec 2679.27 sec
Overall Time 630.5 sec 2684.43 sec
The ratio of number of rays per seconds for continu-
ous rays (KD-tree accelerated ray-object intersection)
and discrete rays in 2.75%, For Scene 2, the ratio of
number of rays per seconds for continuous rays and
discrete rays in 1.33%. This result shows the rele-
vance of the discrete linear method, even more so for
complex scenes. Moreover, the discrete number of
rays per seconds is little dependant on the scene com-
plexity.
In (Hasan et al., 2007) Hasan et al. render sim-
ilar views of the Sponza atrium in about 8s, but we
can not compare that directly since it uses hardware
acceleration vs our fully software single thread based
raytracer, Moreover we used area light to simulate day
light, which is slower than a single ray sunlight. Qual-
ity of the image of (Hasan et al., 2007) may be also
lower since it uses the same set of lights for whole
image, contrary to the lightcuts which selects lights
adaptatively.
6 CONCLUSIONS AND FUTURE
WORK
Our results show that our voxel based method can
be competitive and accurate for precise multi-bounce
global illumination. It provides very large numbers
of rays per seconds for discrete rays, which make
the technique promising. To improve the method, we
could possibly find a method with linear complexity
with respect to the number of rays for the reconstruc-
tion process also, which could result in dramatic re-
duction of the reconstruction time, which is the dom-
inant term. Then, a GPGPU acceleration for the dis-
crete linear method could result in a very low-time
propagation phase, and should be considered. The
current version of the method works only for Lam-
(a) Scene 1: Polygonal scene with 1.176 triangles. Shooting
and multicache methods combined are 6.1 sec. The recon-
structions phase lasted 630 sec. We used 108,455 voxels and
146 directions.
(b) Scene 2: Sponza atrium. Highly textured scene with
67,462 triangles. We used huge area light to simulate day
light. Shooting and multicache methods combined lasted
4.15 sec. We used 22, 615 voxels and 256 directions.
Figure 4: Test scenes.
bertian material, and a method for general BRDF’s
should be developed, by storing a more complex rep-
resentation of outgoing light in voxels. Finally, we
could find a method for fast animation by enabling to
add an object into the scene without recomputing the
whole solution by the use of antiradiance (Christensen
and Batali, 2004).
REFERENCES
Arikan, O., Forsyth, D. A., and O’Brien, J. F. (2005).
Fast and detailed approximate global illumination
by irradiance decomposition. ACM Trans. Graph.,
24(3):1108–1114.
Chatelier, P. Y. and Malgouyres, R. (2006). A low-
CACHED MULTI-BOUNCE SOLUTION AND RECONSTRUCTION FOR VOXEL-BASED GLOBAL
ILLUMINATION
177

complexity discrete radiosity method. Computers &
Graphics, 30:37–45.
Christensen, P. H. and Batali, D. (2004). An irradiance atlas
for global illumination in complex production scenes.
In Rendering Techniques, pages 133–142.
Dachsbacher, C. and Stamminger, M. (2006). Splatting in-
direct illumination. In SI3D, pages 93–100.
Dachsbacher, C., Stamminger, M., Drettakis, G., and Du-
rand, F. (2007). Implicit visibility and antiradiance for
interactive global illumination. ACM Trans. Graph.,
26(3):61.
Debled-Rennesson, I. (1995).
´
Etude et reconnaissance des
droites et plans discrets. PhD thesis, Universit
´
e Louis
Pasteur, Strasbourg. PhD thesis.
Granier, X. and Drettakis, G. (2004). A final reconstruction
approach for a unified global illumination algorithm.
ACM Trans. Graph., 23(2):163–189.
Hasan, M., Pellacini, F., and Bala, K. (2007). Matrix row-
column sampling for the many-light problem. ACM
Trans. Graph., 26(3):26.
Jensen, H. W. (1996). Global Illumination Using Photon
Maps. In Rendering Techniques ’96 (Proceedings of
the Seventh Eurographics Workshop on Rendering),
pages 21–30, New York, NY. Springer-Verlag/Wien.
Jensen, H. W. (1997). Rendering caustics on non-
Lambertian surfaces. Computer Graphics Forum,
16(1):57–64.
Jensen, H. W. (2001). Realistic image synthesis using pho-
ton mapping. A. K. Peters, Ltd., Natick, MA, USA.
Keller, A. (1997). Instant radiosity. In Proceedings of
the ACM SIGGRAPH Conference (SIGGRAPH-97),
pages 49–56, New York. ACM Press.
Lavignotte, F. and Paulin, M. (2003). Scalable photon splat-
ting for global illumination. In GRAPHITE, pages
203–210.
Malgouyres, R. (2002). A discrete radiosity method. In
Braquelaire, A. J.-P., Lachaud, J.-O., and Vialard, A.,
editors, DGCI, volume 2301 of Lecture Notes in Com-
puter Science, pages 428–438. Springer.
Miksik, M. (2007). Implementing lightcuts. In In Cen-
tral European Seminar on Computer Graphics for stu-
dents.
Sillion, F. and Puech, C. (1994). Radiosity and Global Il-
lumination. Morgan Kaufmann Publishers, San Fran-
cisco.
Walter, B., Fernandez, S., Arbree, A., Bala, K., Donikian,
M., and Greenberg, D. P. (2005). Lightcuts: a scal-
able approach to illumination. In SIGGRAPH ’05:
ACM SIGGRAPH 2005 Papers, pages 1098–1107,
New York, NY, USA. ACM Press.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
178