PARALLEL LOSSY COMPRESSION FOR HD IMAGES

A New Fast Image Magnification Algorithm for Lossy

HD Video Decompression Over Commodity GPU

Luca Bianchi, Riccardo Gatti, Luca Lombardi

Computer Vision Lab, University of Pavia, Via Ferrata 1, Pavia, Italy

Luigi Cinque

Department of Computer Science, University of Roma “La Sapienza”, Via Salaria 113, Roma, Italy

Keywords: GPU, Image compression, Parallel algorithms.

Abstract: Today High Definition (HD) for video contents is one of the biggest challenges in computer vision. The

1080i standard defines the minimum image resolution required to be classified as HD mode. At the same

time bandwidth constraints and latency don’t allow the transmission of uncompressed, high resolution

images. Often lossy compression algorithms are involved in the process of providing HD video streams,

because of their high compression rate capabilities. The main issue concerned to these methods, while

processing frames, is that high frequencies components in the image are neither conserved nor

reconstructed. Our approach uses a simple downsampling algorithm for compression, but a new, very

accurate method for decompression which is capable of high frequencies restoration. Our solution Is also

highly parallelizable and can be efficiently implemented on a commodity parallel computing architecture,

such as GPU, obtaining extremely fast performances.

1 INTRODUCTION

From the beginning of multimedia era bandwidth

and memory issues, together with poor video

resolution for TV screens, constrained all standards

for digital video to a resolution of 720x540 pixels.

Broadband internet connections and affordable

prices for memories and displays made available

higher resolutions for video contents in the last few

years. Today the request for higher resolution

content is rising at an amazing rate. Due to the

incredible low cost of consumer electronics, HD

devices for playback are now really inexpensive, but

still many challenges have to be faced: a lots of

standard definition videos are still available and

need to be displayed on HD displays, high resolution

cameras prices still remain high and bandwidth

constraints don’t allow uncompressed transmission.

This means that both decompression and

magnification methods are involved in the process.

Another significant issue, concerned to these

solutions is that often lossy methods are employed to

achieve best compression, taking final images to

poor quality and aliasing effects. Several works

demonstrate that this accuracy reduction is mainly

due to high frequencies loss. We focused our

attention to downsampled images, accounting the

compression step only by a simple algorithm for

image size reduction. We decided not to involve

complex compression methods maintaining as

compressed image a file which still has some

similarities with original image. This choice was due

to the need for flexibility: using as compressed

image a downsampled version of real one, makes

our solution suitable for future works in pre-filtering

or feature extraction without any needing for

decompression. Another interesting aspect of this

approach is that compressed images from HD

streams and legacy low resolution movies are treated

in the same way, making them both a suitable input

for our system. The key phase of this proposed

method is obviously the image magnification

algorithm. We then developed a fast, accurate

magnification algorithm, able to reconstruct high

frequency components (i.e. edges) of original image.

Bianchi L., Gatti R., Lombardi L. and Cinque L. (2009).

PARALLEL LOSSY COMPRESSION FOR HD IMAGES - A New Fast Image Magniﬁcation Algorithm for Lossy HD Video Decompression Over

Commodity GPU.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 16-21

DOI: 10.5220/0001767900160021

 SciTePress

We started our work considering one of the most

employed magnification methods is bilinear

interpolation but, as is shown in the next paragraph,

resultant images are often blurry and the quality is

not acceptable for our purposes, because no adaption

is performed to manage edge crossing.

Paragraph 2 presents the state of the art in image

magnification for video contents, discussing about

usually employed algorithms. In section 2.2 some

interesting results providing acceptable quality are

presented, but their computational cost makes them

unusable for real time video. Paragraph 3 introduces

SIMD architecture and presents some useful results

in HPC which can help looking for a solution and

explains why they can’t be used in known

algorithms. In paragraph 4 our solution, which can

address both accuracy and speed issues, is shown.

After this, paragraph 5 presents algorithm speed and

quality performances. Also an error estimation

method is proposed to evaluate the effective

capabilities of the algorithm against bilinear

interpolation, the only one which could compute in

real-time. Last paragraph reports conclusion and

some ideas we would like to investigate in the near

future.

2 STATE OF THE ART

Usually we have to face with a common drawback

which puts magnification accuracy on one side and

speed on the other. In this paragraph the two

different approaches are shown. In the last section

some words about High Performance Computing

(HPC) techniques are spent to present a way that,

under certain hypothesis, could fulfil all our

requests.

It’s important to clarify that, independently from

the algorithm, image magnification means we have

to estimate colour values for new pixels inserted

between two or more following points in the source

image. Pixel estimation is fundamental because

impacts significantly on the resultant image. A

scarce and imprecise estimation, can introduce

components in colour space that doesn’t exist,

making decompressed image look like a distorted

version the original one. This process, means that,

given an unknown function (1) which represents

pixel value P, for a source image, a magnification

algorithm gives an estimation of  starting from

some random generated samples.











,



,



,





(1)

2.1 Fast but not Accurate

Only two magnification algorithms are usually

employed for everyday real-time magnification:

bilinear (Yan, 1977) and bicubic (Gonzales, 1977)

interpolation. The first one is a fast and naive

approach which uses the approximation described in

(1), given an image expressed as a function I, and

considering only the x coordinate. This is a naive

approach capable of fast computation, but its main

drawback is the lack of precision, which provides

poor quality images introducing many blurring

artefacts.









,

















(2)

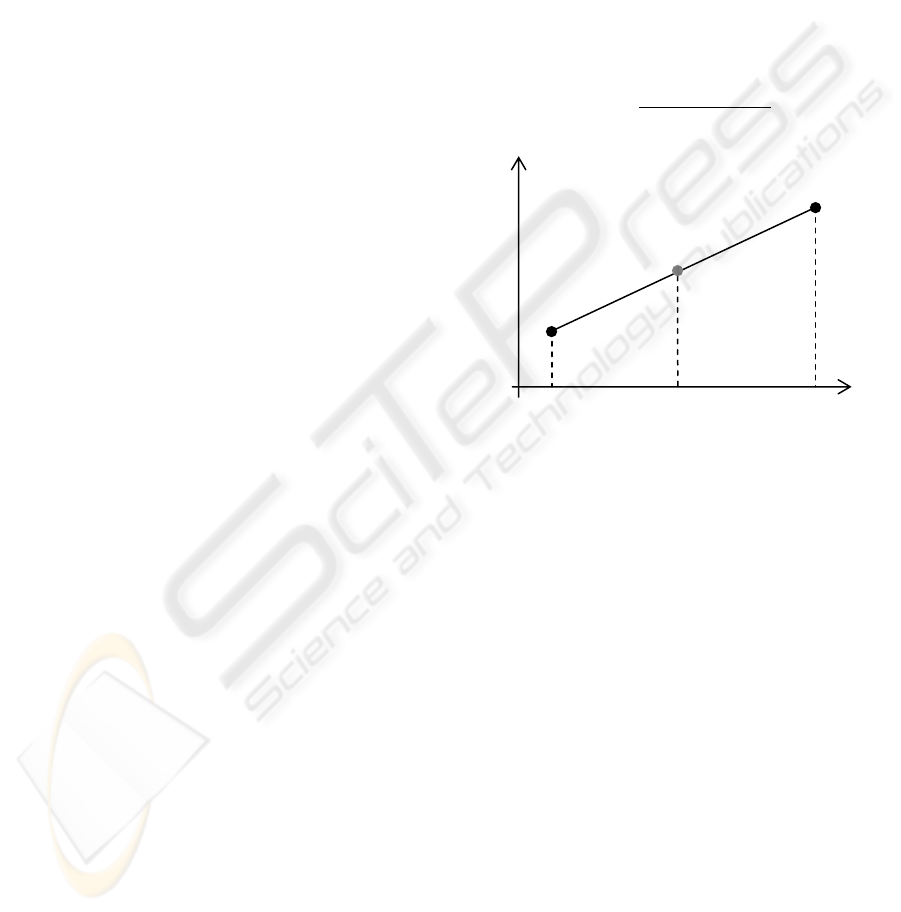
Figure 1: Bilinear interpolation scheme: every new pixel is

defined using a linear function.

Bilinear interpolation uses the very strong

assumption of linear variation of pixel color

intensity in the magnified image (Figure 1). If we

consider colour space This is often inadequate in a

lot of real cases and shows its limits especially when

we have discontinuities in color intensity variation.

By this way the strong variation implied by an edge

inside the original image, is distributed during

magnification on every new inserted pixel in a

uniform fashion. This takes to strong reduction of

image frequency, where a discontinuity is

approximated by a linear function. The result is that

we introduce many unwanted smoothing artefacts,

due to imperfect estimation. This algorithm works

fine for quite uniform or for gradient varying

images.

Bicubic interpolation, takes to slightly

improvements because image spectrum is not but

again no knowledge about edge position is used.

Instead, bicubic interpolation uses a higher

neighbourhood than bilinear and a third order

interpolating function. Results are still unacceptable

for HD purposes.

I(x

B+1

)

k

k+1

I(x

)

PARALLEL LOSSY COMPRESSION FOR HD IMAGES - A New Fast Image Magnification Algorithm for Lossy HD

Video Decompression Over Commodity GPU

Using algorithms such these ones many relevant

features such as edges have their frequency reduced

are inadequate because act as a low-pass filter over

the image, introducing the aliasing effect shown in

figure 2.a and 2.b. The proposed algorithm is also

compared with the nearest neighbor technique for

image magnification in terms of proposed distortion

measure and similarity measure. Nearest-neighbor is

the simplest method of digital magnification. Given

an image of size w×w, to magnify it by a factor k,

every pixel in the new image is assigned the gray

value of the pixel in the original image which is

nearest to it. This is equivalent to repeating the gray

values k×k times to obtain the magnified image. The

resultant image for large magnification factors will

have prominent block like structures due to lack of

smoothness. This sure can in some way preserve

high frequencies, but edge distortions often occurs,

as shown in figure 2.c.

Figure 2: Image magnification (4X) using traditional

algorithms: original image (a), the aliasing effect produced

by bilinear algorithm (b) and the edge distortion

introduced by nearest neighbor (c).

2.2 Accurate and Expensive Image

Magnification

As edges are high spatial frequency features, they

strongly affect perceived image sharpness and

quality. If we assume that the low resolution image

is a sub-sampled version of the high resolution one,

an estimation of edge position is possible,

considering derives for a couple of pixels. This

spatial information can be used to reconstruct edges

and preserve high frequency points. Therefore, edge

estimation must be sub-pixel and the reconstruction

of the HR image must take into account the

estimation results. The idea consists of modifying a

common interpolation scheme, e.g. bilinear or

bicubic interpolation, to prevent interpolation across

edges.

Some solutions in literature involve iterative

algorithms such as fractals (Cheung-Ming, 2004) or

statistical methods (Sang, 2007) to detect edge

position. Unfortunately these methods aren’t capable

of a fast computation, especially due to their non

locality nature. This makes them unsuitable for real

time purposes.

The main idea behind these approaches is that an

edge, which could exist between two neighbor pixels

of the original image, can be easily estimated by an

iterative method. After this, magnified image pixels

values can be easily estimated with good accuracy.

These solutions produce less blurry images than

bilinear or bicubic interpolation, but usually require

a lot of time and can’t take advantage of efficient

parallel computation on commodity hardware.

Estimating edge positions without iterative

methods, then performing a reconstruction seems to

be the best choice for good accuracy and fast

computation.

In literature several magnification methods are

proposed (Keys, 1981) (Allebach, 1996) (Schults,

1992), but everyone uses edge information from low

resolution images. One significant result towards

accurate edge estimation is achieved by (Biancardi,

2001). In this work a method for edge estimation is

given by a convolution filter mask. The main idea

behind this solution is using an accurate center-on-

surround-off filter, which is equal to a mask

developed by the difference of two Gaussians.

Mask uniformity along every possible axis can

take to a convolution result which is direction-

independent. After this operation, considering two

following points in the original image, we will be

able to detect if moving from one to another, an edge

is crossed. This information is used to approximate

the edge by a sigmoid curve and, with knowledge

about derives value in the two original points, the

non-subsampled image is reconstructed. With these

result, an easy sampling process takes to magnified

image. If no edge is found, a bilinear interpolation is

performed.

The main issue concerned by this approach is

about computation performances. The algorithm is

very slow while performing enhancement. The most

of computation time is spent performing convolution

and calculating derives for sigmoid function.

Unfortunately, computational time of more than a

second per frame for a standard DVD image

resolution makes this method unsuitable for real

time purposes.

Performances could be improved using a parallel

computing approach (Cannataro, 2002) (Luebke,

2004), a well known technique in High Performance

Computing (HPC). The most interesting thing about

that is a speedup gain for computation which often

can be hundreds time faster than equivalent run over

CPU. Unfortunately for our needs, parallel

computing involves some strong constraints which

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

cannot be broken without heavily compromising

computation gain. One of the most important of

these constraints is the use of local data for

processing. Localization is meant both in reading

and writing data. This is not true for (Biancardi,

2001) where 4 points neighbourhood is not enough

for derives estimation, so image cannot be broken

into n four points subset. We started from this point

to develop our magnification algorithm which was

required to fulfil every parallel computing

constraint.

3 GPGPU FOR MAGNIFICATION

Since many years GPUs have evolved toward a

general purpose architecture. This idea was

supported by the adoption of a stream processing

SIMD architecture which could perform a single

instruction on multiple data in a single execution

step (Akenine-Moller & Haines, 2002).

GPGPU figures out how to use the graphical unit

for general elaborations, in an efficient way. Parallel

image elaborations were one of the first algorithms

developed using graphic cards for general purposes.

The advent of Computer Unified Device

Architecture (CUDA) allowed a more efficient

approach to image elaboration and important

improvements such as separable convolution

(Podlozhnyuk, 2007) were found to provide even

faster computation than traditional GPGPU

approach.

One of the most significant limits of GPGPU

efficiency is that it is still constrained by graphics

concepts and computing is done using graphic

hardware as a black box. This takes to the fact that

each stream processor (a SIMD module on the GPU)

should work alone without sharing data from another

processor.

4 A FAST ALGORITHM FOR

IMAGE DECOMPRESSION

Efficient algorithm parallelization is very difficult

and often not possible. The proposed solution is

developed starting from (Biancardi, 2001) moving to

a SIMD architecture. We preserved the main idea of

edge estimation, to detect pixels colour and built an

algorithm suitable for our real-time purposes. Our

algorithm, named IMAF, uses a convolution edge

detection which performs convolution with two

uniform radial mask. Each mask has a defined

weight, different size and opposite sign.

Using two different convolution masks allow

efficient parallelization of filtering algorithm and

takes to improved efficiency. Following the idea

exposed in (Podlozhnyuk, 2007), each mask has

been expressed splitted into two array, to define a

separable filter mask. This technique made our

double convolution to compute in a more efficient

way, performing coalesced sequential accesses to

image, stored in shared memory. Coalesced memory

accesses are the best solution to reach optimization

over a SIMD architecture (nVidia, 2008).

Separable filters are a special type of filter that

can be expressed as the composition of two one-

dimensional filters, one on the rows on the image,

and one on the columns. A separable filter can be

divided into two consecutive one-dimensional

convolution operations on the data, and therefore

requires only n + m multiplications for each output

pixel. Using this approach the requirement for data

locality, fundamental in SIMD algorithms has been

addressed.

The other critical part in image magnification is

non sub-sampled image reconstruction and data

interpolation. The proposed solution takes account

of high frequency components preserving, by using

two different interpolation functions. The Sigmoid

Function, proposed in (Biancardi, 2001) was

discarded due to its computational costs in derives

estimation. Our algorithm simply detect if an edge is

highlighted by filtered image. This is easily

performed because considering two following

pixels, their corresponding value in our filtered

image is retrieved. If the product of these values is

negative, we can assert that in the original,

uncompressed image an edge is between them. Also

the position of this edge can be estimated, supposing

that pixel distance is constant and that between two

samples no more than an edge is crossed. If no edge

is crossed, corresponding pixels have the same sign

and a simple bilinear interpolation can be performed

with acceptable results. After edge position is

known, an interpolation function, accounting this

information has to be used. For this reason, we

defined a function for pixel colour estimation before

the edge and another after. Two first order functions

can be used, because no continuity in colour space

has to be addressed if an edge is crossed. Given two

following pixels A, B in compressed image and an

edge point between them detected by our filter, we

can describe our reconstruction function as follows.

We can define 



and 



respectively A and B

coordinates along one direction, 



and 



their

PARALLEL LOSSY COMPRESSION FOR HD IMAGES - A New Fast Image Magnification Algorithm for Lossy HD

Video Decompression Over Commodity GPU

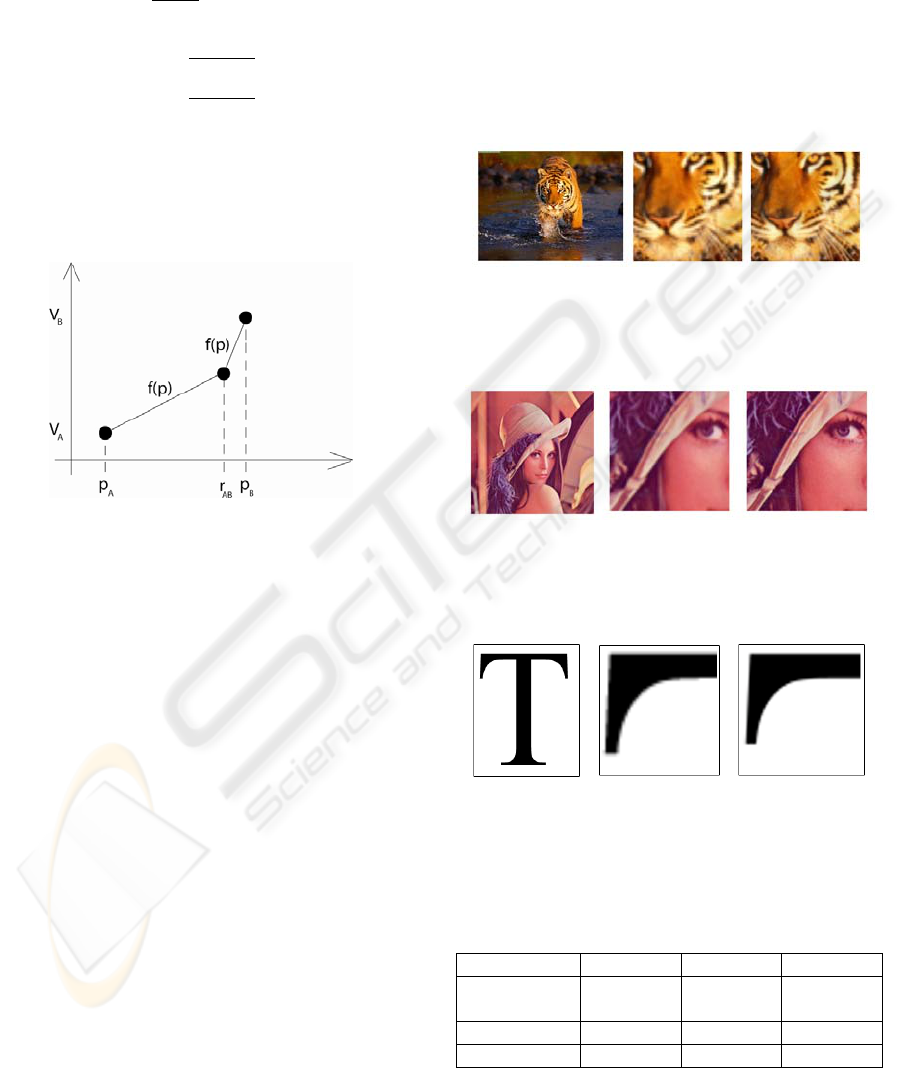
values in color space and 



detected edge point

coordinate along the same given direction. Colour

value 



in 



, is defined by equation (3) and

interpolating function is expressed by (4).

















(3)



























,



























,



(4)

This function performs a linear interpolation

between A and edge point and from edge point to B,

respecting discontinuity of derives in colour space

due to high frequency components in edges as

described in Figure 3.

Figure 3: Interpolating function for high frequency

reconstruction.

This function performs interpolation first on

image rows and after on columns. These steps can

be easily parallelized because there are no data

constraints between them. A further parallelization is

done by processing many image pixel subsets at

same time. By this way a two level parallelization is

introduced, which should give best performances.

5 PERFORMANCE ANALYSIS

Evaluation has been computed on still images,

measuring correctness and execution time. To

demonstrate the capabilities of our method we chose

three particular test images, reported in figure 4, 5

and 6. The first two are substantially common

images, while the third one is a particular interesting

case where traditional approaches show their limits.

This is due to the presence in the image of high

frequency components. Original Image is assumed

to be the compressed data received from our stream.

In order to evaluate algorithms performances on

useful cases, an enhancement factor of 4X has been

considered. This is necessary to consider a solution

capable of providing HD content from highly

compressed images or standard 720x570 frames.

Algorithm efficiency can be measured by

evaluating execution time. The noticeable

improvement of the proposed algorithm respect to

bilinear interpolation is shown in Table 1.

We propose a method for precision estimation in

enhanced images. Starting from a high resolution

image, a 4x sub sampling is applied, then images are

magnified using both bilinear and IMAF algorithms.

Figure 4: subsampled image of 400x300 pixels is shown

in(a), a 4x magnification, using bilinear algorithm(b) and

our method which produces more defined images(c).

Figure 5: subsampled image of 512x512 pixels is shown in

(a), a 4x magnification, using bilinear algorithm (b) and

our method which produces more defined images (c).

Figure 6: An image of 400x500 pixels, with many high

frequency components (a), a 4x bilinear magnification

introduces many artifacts. IMAF algorithmprovides better

results (c).

Table 1: Execution times.

ure 4 Fi

ure 5 Fi

ure 6

Bilinear

interpolation

102 ms 112 ms 88 ms

IMAF CPU 111 ms 124 ms 98 ms

IMAF GPU 35 ms 38 ms 22 ms

b c

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

Table 2: Error Rates.

ure 4 Fi

ure 5 Fi

ure 6

Bilinear

interpolation

48,32% 36,95% 11,2%

IMAF CPU 37,9% 28,4% 5,8%

IMAF GPU 37,7% 28,3% 6,1%

Then error is computed subtracting original

image from magnified one and evaluating it respect

to source image. The evaluation results clearly

shows the quality of our approach. We are capable

of providing fast image magnification algorithm

with a quality noticeable higher than bilinear

method. Another interesting results is that

computation time for GPU implementation doesn’t

grow linearly with image size. This suggest that

hardware utilization is far from 100% and more

efficiency can be obtained using bigger images. This

fact is beyond the scopes of our works, because we

would like using smaller images, but means that

more computational power of the GPU is available

for improvements or different algorithm execution.

6 CONCLUSIONS AND FUTURE

WORKS

The results presented in the above paragraph point

out some interesting conclusions. First of all the

proposed method is suitable for real-time

computation and could be used for stream

processing. A second and more interesting

consideration comes out directly from paragraph 4

and is concerned to hardware utilization due to our

method which uses a small input image. If we could

use a more flexible SIMD architecture, capable of

running more than one program, probably different

algorithms could be executed at the same time: for

example image filtering and interpolation.

Unfortunately GPUs can’t provide this feature. For

this reason, we’re looking interested to other SIMD

solution, such as IBM CELL processor. A future

work taking this method to CELL BE, will be done

because this could represent an interesting solution

also for embedded devices. Although the proposed

algorithm is intended for video stream processing,

no assumptions are done for inter-frame processing.

Matching our method with different lossless

compression algorithms, also accounting inter-frame

analysis could take to different advances and

produce a system for compression at rates higher

than 4-8X. This work is essentially a preliminary

results, and our attention was focused on

magnification method. Further optimization are

thought to be introduced in future works, together

with extensive evaluation on large streams.

ACKNOWLEDGEMENTS

This work has been partially supported by FIRB

Project RBIN043TKY.

REFERENCES

Yan J.K., Sakrison DJ, 1977. Encoding of images based

on a two component source model, IEEE Trans. on

Communications. vol. COM-25, no.11, pp.1315-1322.

Gonzales R.C., P. Wintz, 1977. Digital Image Processing,

MA Addison-Wesley

Cheug-Ming, Lai et al. 2004. An efficient fractal-based

algorithm for image magnification. Proceedings of

2004 International Symposium on Intelligent

Multimedia, Video and Speech Processing, 2004.

Sang Soo, Kim, Il Kyu, Eom, and Yoo Shin Kim, 2007.

Image Interpolation Based on Statistical Relationship

Between Wavelet Subbands. IEEE International

Conference on Multimedia and Expo. pp. 1723 - 1726.

Keys, R.G. 1981. Cubic convolution interpolation for

digital image processing. IEEE Trans. ASSP.

Allebach, J. and Wong, P. W. 1996. Edge-Directed

Interpolation. Lausanne CH : IEEE Press, Proceedings

of the ICIP-96. Vol. III.

Schults, R. R. and Stevenson, R. L. 1992. Improved

definition of image expansion. San Francisco.

Proceedings of the 1992 International Conference.

Biancardi A., Lombardi L., Cinque L. 2001. Improvements

to image magnification. Elseviere Science.

Cannataro, M., Talia, D. Srimani, Pradip 2002. Parallel

data intensive computing in scientific and commercial

applications. Amsterdam, The Netherlands, The

Netherlands: Elsevier Science Publishers B. V., May

Parallel data-intensive algorithms and applications,

Vol. 28. ISSN: 0167-8191.

Luebke, David, et al. 2004. GPGPU: general purpose

computation on graphics hardware. ACM

SIGGRAPH 2004 Course Notes, International

Conference on Computer Graphics and Interactive

Techniques.

Podlozhnyuk, Victor. Image Convolution with CUDA.

http://developer.download.nvidia.com. [Online] June

2007. [Cited: April 24, 2008.]

http://developer.download.nvidia.com/.../1_1/Website/

projects/convolutionSeparable/doc/convolutionSepara

ble.pdf.

nVidia Corporation. CUDA Programming Guide. nVidia

CUDA Web Site. [Online] February 2008.

Akenine-Moller, T., & Haines, E. (2002). RealTime

Rendering. A. K. Peters.

PARALLEL LOSSY COMPRESSION FOR HD IMAGES - A New Fast Image Magnification Algorithm for Lossy HD

Video Decompression Over Commodity GPU