SYMMETRY-BASED COMPLETION

Thiago Pereira

, Renato Paes Leme

, Luiz Velho

and Thomas Lewiner

Visgraf, IMPA, Brazil

Department of CS, Cornell, U.S.A.

Matmidia, PUC–Rio, Brazil

Keywords:

Image completion, Inpainting, Symmetry detection, Structural image processing.

Abstract:

Acquired images often present missing, degraded or occluded parts. Inpainting techniques try to infer lacking

information, usually from valid information nearby. This work introduces a new method to complete missing

parts from an image using structural information of the image. Since natural and human-made objects present

several symmetries, the image structure is described in terms of axial symmetries, and extrapolating the sym-

metries of the valid parts completes the missing ones. In particular, this allows inferring both the edges and

the textures.

1 INTRODUCTION

Acquired images are generally incomplete, either due

to the degradation of the media, like old paintings,

pictures or ﬁlms, due to occlusion of scene parts from

undesired objects or due to channel losses in digital

image transmission. To overcome those issues, in-

painting techniques try to complete missing regions

of an image. Since the ground truth is unknown in

real applications, the inferred content must be consis-

tent with the image as a whole.

This implies two steps in the inpainting pipeline:

analysis and synthesis. The analysis step determines

the characteristics of the image relevant to comple-

tion. The synthesis step then uses the gathered knowl-

edge to extend the valid region. Local methods ana-

lyze the boundary of the invalid region and the synthe-

sis is usually performed by diffusion-like processes to

propagate the boundary’s color. However, the diffu-

sion step may blur the inpainted region, harming the

texture coherency. Other methods segment the image

in texture-coherent regions and synthesize a new tex-

ture to ﬁll the hole, based on the closest match with

the boundary texture. Although this solves the blur

problem, it may not respect the global structure of the

image. In particular, completing very curved shapes

or big holes remains an issue.

In this work, we propose to exploit the global

structure of the image for inpainting (see Figure 7).

More precisely, we estimate the image’s symmetries

and complete the missing part by their valid symmet-

ric match. Since symmetry is an important coherency

criterion both for natural and human-made objects, its

analysis reveals much of the relevant image structure.

The present paper restricts to axial symmetries of the

image’s edges, and may be easily extended to entail

more general transformations and features. However,

nice results, including textures, can already be ob-

tained with these restrictions. This research started

as a project for the course ”Reconstruction Methods”

at IMPA in fall 2007.

2 RELATED WORK

Since this work applies symmetry detection to inpaint

missing regions of an image, we’ll ﬁrst review pre-

vious method of image restoration followed by works

on symmetry, both from computer vision and geomet-

ric modelling.

2.1 Image Restoration

Inpainting methods can be categorized according to

the extent of the region the analysis and synthesis op-

erations work on. Early approaches use local analysis

to extend the valid image from a small neighborhood

around the missing region. In particular, (Bertalmio

et al., 2000) propagate image lines (isophotes) into

the missing part using partial differential equations,

interleaving propagation steps with anisotropic dif-

fusion (Perona and Malik, 1990). This extends the

smooth regions while still respecting image edges.

(Petronetto, 2004) created an inpainting algorithm

inspired by heat diffusion to improve propagation.

These local methods work very well for small holes

Pereira T., Paes Leme R., Velho L. and Lewiner T.

SYMMETRY-BASED COMPLETION.

DOI: 10.5220/0001655900390045

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications (VISIGRAPP 2009), page

ISBN: 978-989-8111-67-8

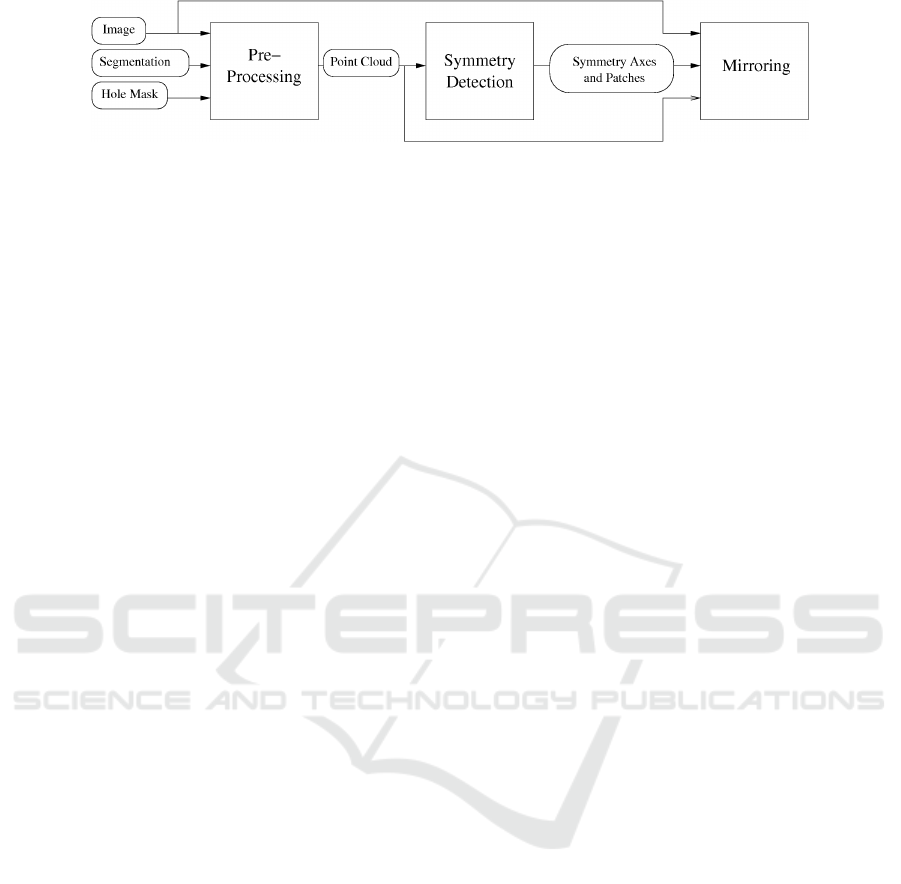
Figure 1: The input image is pre-processed to extract a sampling of the edges. The symmetry detection extracts the structure

of this point cloud, and these symmetries are used for completing the missing parts by mirroring adequate valid parts.

but introduce blur when dealing with large regions,

which harms the quality of results on regions with

high frequencies and texture. Global analysis try to

locate relevant regions in the entire image, or even

in a large image database (Hays and Efros, 2007) to

handle very large missing regions if similar objects

are present in the database.

On the synthesis side, several approaches consider

completion as a texture synthesis problem: instead

of completing at a pixel level, these methods iden-

tify small regions of the hole to be ﬁlled ﬁrst and

search for a best match throughout the image. The

matched region is copied and blended with the sur-

roundings. In particular, (Efros and Freeman, 2001)

create new textures by putting together small patches

from the current image. (Drori et al., 2003) and (Cri-

minisi et al., 2003) complete the holes by propagat-

ing texture and contours. These methods preserve lo-

cal structure of the image, but may fail to propagate

global structure of the image like bending curves. In

this work, we propose a technique that identiﬁes the

object structure and boundaries and incorporate this

information in the completion process. We argue that

structure from object symmetry can be used for in-

painting in more complex examples.

2.2 Symmetry Detection

Early works in symmetry detection deal with global

and exact symmetries in point sets (Wolter et al.,

1985) based on pattern-matching algorithms. This

restricts their applicability to image processing since

most symmetries found in nature or human-made are

not exact or might be slightly corrupted by noise.

(Zabrodsky et al., 1995) measures the symmetry of a

shape by point-wise distance to the closest perfectly

symmetric shape. The level of symmetry can also

be measured by matching invariant shape descriptors,

such as the histogram of the gradient directions (Sun,

1995), correlation of the Gaussian images (Sun and

Sherrah, 1997) or spherical functions (Kazhdan et al.,

2004). Such symmetry measures work well for de-

tecting approximate symmetry, although they are de-

signed for global symmetry detection.

Recently, (Loy and Eklundh, 2006) used the

Hough Transform to identify partial symmetries, i.e.,

symmetries of just one part of the object. Such partial

symmetries can also be obtained by partial matching

of the local geometry (Gal and Cohen-Or, 2006). In

particular, (Mitra et al., 2006) accumulates evidences

of larger symmetries using a spatial clustering tech-

nique in the symmetry’s space. The technique used in

this paper is close to (Mitra et al., 2006). However,

we focus on incomplete symmetries due to occlusion

in images, and thus adapted their symmetry detection

for 2D shapes.

Symmetries have been used to complete shapes

in different contexts. For example, (Thrun and Weg-

breit, 2005) detects symmetries in 3D range image to

complete based on a search in the symmetry space,

and complete the whole model by a global reﬂection.

(Zabrodsky et al., 1993) uses a symmetrization pro-

cess to enhance global symmetry, even with occluded

parts. (Mitra et al., 2007) achieves similar results for

3D shapes. However, these techniques do not handle

partial symmetries or affect parts of a 2D image that

are not missing.

3 METHOD

We start this section with a brief overview of the pro-

posed method followed by the details of our process.

3.1 Overview

The proposed method is composed of two main steps:

symmetry detection, corresponding to the image anal-

ysis, and mirroring for synthesis of lacking informa-

tion. The interactions between these steps is schema-

tized in Figure 1 and illustrated in Figure 2. The in-

put image contains a user-deﬁned mask around the in-

valid region. A simple pre-processing extracts from

the image a structured sampling of its edges (see Fig-

ure 2(a)-(d)) from which the normal and curvature is

computed. Then, the symmetry detection step identi-

ﬁes the many symmetry axes present in the object, as

seen in 2(f). Finally, the completion step chooses the

symmetry axis that best ﬁts the missing region and

mirrors the texture and edges of the valid parts into

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

(a) Input texture. (b) Segmentation. (c) Hole mask. (d) Edge image.

(e) Edge’s points. (f) Axes and patches. (g) Mirroring. (h) Final image.

Figure 2: Illustration of the pipeline of Figure 1.

the hole (Figure 2(g)-(h)). These steps are detailed

below.

3.2 Pre-processing: Object Extraction

Object identiﬁcation is a well studied problem. Many

algorithms have been proposed to segment images.

While extremely relevant to our method, segmenta-

tion is not the focus of this work. As such, we assume

receiving a segmented image as input. Symmetry ex-

traction should ideally take into account the border as

well as the interior of the image’s objects. We use

here only the border (edge) information for the sake

of simplicity. Moreover, we represent those edges by

points. Although it may lose some connectivity infor-

mation, it permits a versatile representation and ﬁts

better for adapting geometric modeling techniques for

symmetry detection. Therefore, we perform an edge

detection on the input image through a difference of

Gaussians implemented in the GIMP package (Mattis

and Kimball, 2008), and remove the artiﬁcial edges

generated from the user-deﬁned hole mask. We then

perform a stochastic sampling of the edges taking the

gray values of the edge image as probability. This

generates a point set representation of the edges. Fi-

nally, we compute the normal and the local curvature

at each point of the point set.

3.3 Analysis: Symmetry Detection

We are interested in approximate and partial symme-

tries, since the image has incomplete information in

the hidden regions and since the image content may

present several inexact symmetries. Therefore, our

approach is largely based on the method proposed by

(Mitra et al., 2006). However, in this paper, we will

restrict the space of symmetries to axial symmetries.

Using the point set representation described above,

valid partial symmetries should map a substantial sub-

set of the points to another one. In its basic form, the

symmetry detector stores for each pair of points their

bisector as a candidate symmetry axis (see Figure 3).

Then it returns the clusters of candidates with their

associated matching regions. The clustering allows

detecting approximate symmetries.

To improve robustness and efﬁciency of this ba-

sic scheme, we have enhanced this basic scheme as

follows. On the one hand, we can observe that the

sampling of the edges does not guarantee that a point

p of the set is the exact symmetric of another sample

point q. However, their normals should be mapped

even with random sampling. Therefore, we deﬁne for

each pair pq the candidate reﬂection axis T

as the

line passing through the midpoint of pq and parallel

to the bisector of the normals at p and q (see Figure

3). The normals are then symmetric by T

, although

the points p, q may not be. On the other hand, reduc-

ing the number of candidate axes would accelerate the

clustering. Notice that pairing points outputs O(N

)

axes. Therefore, we only accept a pair p,q if their

curvatures are similar (0.5 < |K

| < 2), since the

curvature is covariant with reﬂections. We also reject

a candidate axis T

deﬁned above if points p and the

reﬂection of q are farther than 3.5% of the image’s

diagonal.

Figure 3: Symmetry axis robustly deﬁned from normals.

SYMMETRY-BASED COMPLETION

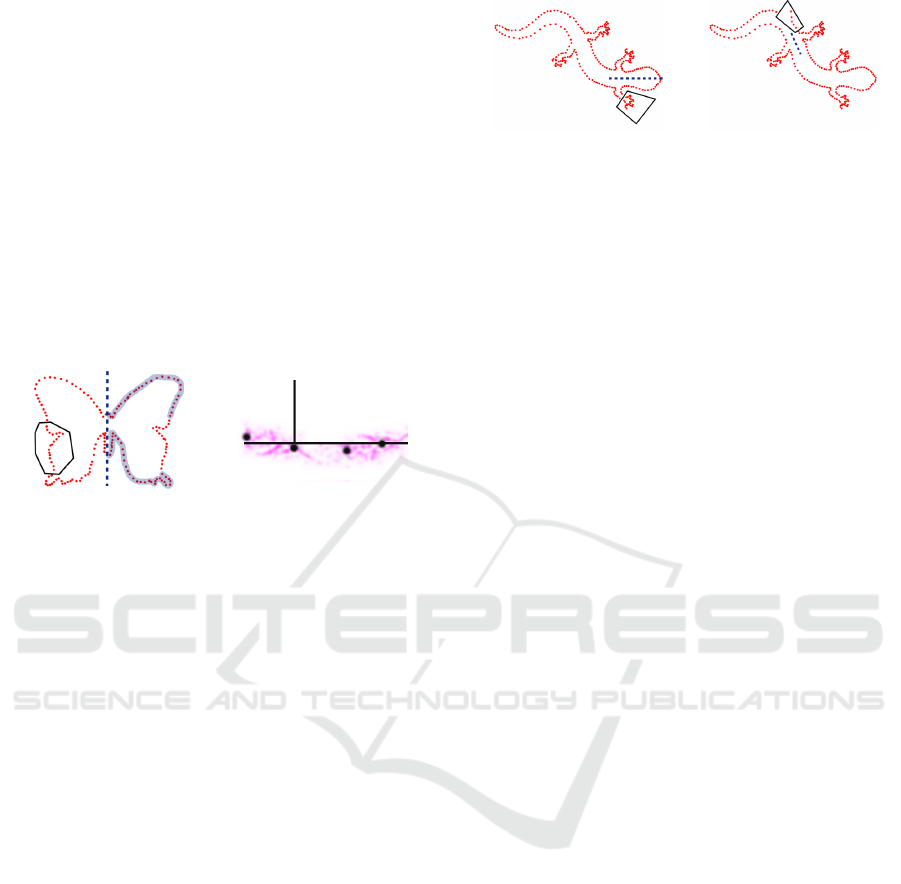
The ﬁltered candidate axes are then represented by

their distance to the origin and their angle φ ∈ [0, π[

with respect to the horizontal line (see Figure 4).

Clustering is performed in this two-dimensional pa-

rameter space using Mean-Shift Clustering (Comani-

ciu and Meer, 2002), taking into account the inver-

sion at φ = π. Given a candidate axis T

at the cen-

ter of a cluster, we deﬁne its matching region to be

the set of point pairs invariant by reﬂection through

. We compute it by propagating from the initial set

S = {p,q}: a neighbor r of a point s ∈ S is added

if its reﬂection through T

is either close to some

point of the object boundary or inside the hole mask.

This last condition allows detecting incomplete sym-

metries, which are crucial for completion.

(a) Symmetry axis. (b) Axis density.

Figure 4: Clustering of candidate symmetry axis.

3.4 Synthesis: Texture Generation

The completion process ﬁrst identiﬁes from the ob-

ject structure which of the detected symmetries to use,

and then reﬂects the image’s texture from visible re-

gions into the occluded one. The ideal situation for

our structural completion occurs when a single sym-

metry’s matching region traverses the hole. In that

case, the sampled points around the hole clearly de-

ﬁne which visible region of the image is to be re-

ﬂected. More precisely, the ﬁlled boundary must ﬁt

the known object boundary. In Figure 5(b) there was

a discontinuity. We thus choose among all detected

symmetries the one that best ﬁts the created points

with the known boundary.

However, in many real cases, in particular those

with large missing parts, no mapping with a sin-

gle symmetry axis would create a continuous object

boundary (see Figure 5). To overcome this issue, we

complete the boundary from the hole border inwards.

To do so, we look for the symmetry that maps the

most points while enforcing continuity in the neigh-

borhood of the hole border (see Figure 9). This pro-

cess repeats itself until either we arrive at a closed

boundary or no symmetry axis satisﬁes the continuity

requirement.

Once the axes have been deﬁned and the valid

structures have been mapped to the hole, we proceed

to the image-based completion. For each pixel i of

(a) Successful. (b) Failed.

Figure 5: A single axis achieves continuity on both sides of

the hole.

the hole, we look for the closest point p of the ﬁlled

boundary. This point p has been reﬂected by a sym-

metry T which is used to ﬁnd the symmetric pixel j of

i. The color of j is simply copied into i. This approach

is very simple and may be enhanced in future works

by more advanced texture synthesis and insertion.

4 RESULTS

In this section we ﬁrst detail the implementation, fol-

lowed by a description and analysis of the experi-

ments.

4.1 Implementation Details

The method described at the previous section can

be implemented with different algorithmic optimiza-

tions. During many steps of our algorithm, proximity

queries were required. Therefore, we build a Delau-

nay triangulation at pre-processing in order to sup-

port k-nearest-neighbors queries. Among other al-

ready mentioned uses, these queries serve the normal

and curvature approximations by a local second de-

gree polynomial Monge form. In order to choose efﬁ-

ciently the best axis that maps a valid structure to the

hole’s edge, we build a proximity graph. The vertices

of this graph are the valid structure points that are mir-

rored into the hole. A link between vertices is created

when they have a common symmetry axis T and when

their reﬂection by T are close-by. The longest path in

that graph determines the best symmetry axis T .

4.2 Experiments

We experimented our technique in different contexts

using images from public domains. Table 1 presents

the execution times including the entire pipeline. The

symmetry detection step accounts for 85% of total

time. The butterﬂy image of Figure 7 has symmetric

structures and background with the same axis. The

eagle image of Figure 6 has symmetric structures for

the main shape, but the background has a different

symmetry. On the contrary, the turtle image of Figure

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

8 has a symmetric background but the animal’s sym-

metry is artiﬁcial, although very coherent with the im-

age. The lizard structure of Figure 5 was tested in two

opposite conﬁguration: perfect symmetric and lack of

symmetry. Our method runs in quadratic time, but is

very sensitive to the pruning step.

Table 1: Timings (seconds) on a 2.8 GHz Pentium D.

Model #Points #Symmetries Timing

Butterﬂy 506 12 44

Eagle 765 9 83

Turtle 575 8 46

Lizard hand 271 10 87

Lizard body 294 10 122

4.3 Discussion

We achieve good results even by considering only ax-

ial symmetries and simply copying the image texture

in the unknown region. When the symmetry struc-

tures traverses the holes, the completion of the fore-

ground is neat (see Figure 7 and 8). The quality ob-

tained in Figure 7(d) is a consequence of symmetry

being present in the background also. Only in a de-

tailed inspection, seams can be detected between the

visible and the reconstructed region. These seams can

only be noted in the texture, not in the background.

Our method completes images based on symme-

tries from the image’s edges, and supposes that the

object’s texture is likely to follow the same transfor-

mation. However, this may not be the case. For exam-

ple in Figure 6, the missing wing of the eagle was well

reconstructed from the visible one, although the syn-

thesized background differs in the tone of blue from

the original one. Blending would solve this case.

Our method only works with images where sym-

metry is present. As most objects have symmetries,

this is not a big restriction. In fact coherent results

were found only when one symmetry axis dominated

the hole. The completed objects above are all seen

from well behaved view points. An object can be

symmetric from a point of view while not being from

others. One simple extension is to ask the user to

mark four points deﬁning the plane where the sym-

metry holds. We would then work on a transformed

space where the symmetry axis is contained in the im-

age plane. One advantage of the method is that the

user knows before hand if it will work since he can

usually see the symmetries himself.

5 CONCLUSIONS

In this work, we propose to incorporate global struc-

tural information of an image into inpainting tech-

niques. In particular, we present a method for inpaint-

ing images that deals with large unknown regions by

using symmetries of the picture to complete it. This

scheme is fully automated requiring from user only

the speciﬁcation of the hole. The current technique

restricts itself to the analysis of axial symmetries of

the image’s edges, focusing on structure rather than

texture. On the one hand, the transformation space

can be easily extended using the same framework, in-

corporating translations, rotations and eventually pro-

jective transformations at the cost of using a higher

dimensional space of transformations. On the other

hand, texture descriptors could be used to improve

both the symmetry detection and the image synthesis

(see Figure 10). Moreover, the insertion of the synthe-

sized parts into the image can be improved by exist-

ing inpainting techniques. Another line of work, fol-

lowing (Hays and Efros, 2007), is to build a database

of object boundaries. Completion would proceed by

matching the visible part of the object with those in

the database.

REFERENCES

Bertalmio, M., Sapiro, G., Caselles, V., and Ballester, C.

(2000). Image inpainting. In SIGGRAPH. ACM.

Comaniciu, D. and Meer, P. (2002). Mean shift: a robust

approach toward feature space analysis. PAMI.

Criminisi, A., P

erez, P., and Toyama, K. (2003). Object

removal by examplar-based inpainting. In CVPR.

Drori, I., Cohen-Or, D., and Yeshurun, H. (2003).

Fragment-based image completion. TOG.

Efros, A. A. and Freeman, W. T. (2001). Image quilting for

texture synthesis and transfer. In SIGGRAPH. ACM.

Gal, R. and Cohen-Or, D. (2006). Salient geometric features

for partial shape matching and similarity. TOG.

Hays, J. and Efros, A. (2007). Scene completion using mil-

lions of photographs. In SIGGRAPH, page 4. ACM.

Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2004).

Symmetry descriptors and 3d shape matching. In

SGP. ACM/Eurographics.

Loy, G. and Eklundh, J.-O. (2006). Detecting symmetry

and symmetric constellations of features. In European

Conference on Computer Vision, pages 508–521.

Mattis, P. and Kimball, S. (2008). Gimp, the GNU Image

Manipulation Program.

Mitra, N., Guibas, L., and Pauly, M. (2006). Partial and ap-

proximate symmetry detection for 3d geometry. TOG.

Mitra, N., Guibas, L., and Pauly, M. (2007). Symmetriza-

tion. TOG, 26(3):63.

SYMMETRY-BASED COMPLETION

Perona, P. and Malik, J. (1990). Scale-space and edge de-

tection using anisotropic diffusion. PAMI.

Petronetto, F. (2004). Retoque digital. Master’s thesis,

IMPA. oriented by Luiz-Henrique de Figueiredo.

Sun, C. (1995). Symmetry detection using gradient infor-

mation. Pattern Recognition Letters, 16(9):987–996.

Sun, C. and Sherrah, J. (1997). 3d symmetry detection using

the extended gaussian image. PAMI, 19(2):164–168.

Thrun, S. and Wegbreit, B. (2005). Shape from symmetry.

In ICCV, pages 1824–1831. IEEE.

Wolter, J., Woo, T., and Volz, R. (1985). Optimal algorithms

for symmetry detection in two and three dimensions.

The visual computer, 1(1):37–48.

Zabrodsky, H., Peleg, S., and Avnir, D. (1993). Completion

of occluded shapes using symmetry. In CVPR. IEEE.

Zabrodsky, H., Peleg, S., and Avnir, D. (1995). Symmetry

as a continuous feature. PAMI, 17(12):1154–1166.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

(a) Input image (b) Input image (c) Point cloud and Symme-

tries

(d) Completed image

Figure 6: Eagle example: although the foreground is well completed, the background texture needs further or separate pro-

cessing.

(a) Hole. (b) Axis. (c) Completed image. (d) Completion detail.

Figure 7: Completion of a butterﬂy image: the marked missing region 7(a), in gray, is identiﬁed in the global structure of the

image through axial symmetries 7(b). It can be completed with texture from its symmetric part 7(c),7(d).

(a) Input image (b) Completed image (c) Ground truth

Figure 8: Turtle example: although the completion differs from the original model, it is very coherent.

(a) Input image (b) Half completed image (c) Ground truth

Figure 9: Fish example: a single axis may not ensure boundary coherency on both sides.

(a) Input image (b) Completed image (c) Ground truth

Figure 10: Flower example: texture elements are not yet considered in the analysis.

SYMMETRY-BASED COMPLETION