
VARIABLE SUBSET SELECTION FOR BRAIN-COMPUTER
INTERFACE
PCA-based Dimensionality Reduction and Feature Selection
N. S. Dias
1
, M. Kamrunnahar
2
, P. M. Mendes
1
, S. J. Schiff
2
and J. H. Correia
1
1
Dept. of Industrial Electronics, University of Minho, Campus Azurem, 4800-058 Guimaraes, Portugal
2
Dept. of Engineering Sciences and Mechanics, The Pennsylvania State University, University Park, PA 16802, U.S.A.
Keywords: BCI, EEG, Feature selection.
Abstract: A new formulation of principal component analysis (PCA) that considers group structure in the data is
proposed as a Variable Subset Selection (VSS) method. Optimization of electrode channels is a key problem
in brain-computer interfaces (BCI). BCI experiments generate large feature spaces compared to the sample
size due to time limitations in EEG sessions. It is essential to understand the importance of the features in
terms of physical electrode channels in order to design a high performance yet realistic BCI. The VSS
produces a ranked list of original variables (electrode channels or features), according to their ability to
discriminate between tasks. A linear discrimination analysis (LDA) classifier is applied to the selected
variable subset. Evaluation of the VSS method using synthetic datasets selected more than 83% of relevant
variables. Classification of imagery tasks using real BCI datasets resulted in less than 16% classification
error.
1 INTRODUCTION
Brain-Computer Interfaces (BCI) enable people to
control a device with their brain signals (Wolpaw et
al., 2000). BCIs are expected to be a very useful
tool for impaired people both in invasive and non-
invasive implementations. Non-invasive BCI
operation commonly uses electroencephalogram
(EEG) from human brain for the ease of
applicability in laboratory set ups as well as in
patient applications. Datasets are generally high-
dimensional, irrespective of the types of features
(frequency band power, event-related
desynchronization (ERD), movement-related
potentials (MRP), event-related potentials (e.g.
P300), etc.) extracted from EEG, if no previous
knowledge about those features is considered. The
low ratio of the number of samples to the number of
variables is described as the curse of dimensionality
(Duda et al., 2000). Frequently, in a BCI experiment,
it is not easy to increase the number of samples to
compensate for high-dimensionality. On the other
hand, a variable subset calculation is feasible when
few variables are relevant.
The variables in a dataset can be divided into
irrelevant, weakly relevant and strongly relevant
variables (John et al., 1994). A good subset should
include all the strongly relevant variables and some
of the weakly relevant ones. The variable subset to
choose should minimize the generalization error (i.e.
cross-validation error). Typically, the term ‘feature’
is used in the literature (Yu and Liu, 2004) instead of
‘variable’. Nevertheless, we here use the latter to
avoid confusion about the dimensions of the dataset
(electrode channels) and the characteristic features
(e.g. band power, MRP) extracted from EEG raw
signals.
This work proposes a feature selection method
based on a different formulation of Principal
Component Analysis (PCA), introduced in (Dillon,
1989) that accommodates the group structure of the
dataset. In the PCA framework, data dimensionality
reduction methods typically use the selected
principal components (PC) as a lower-dimensional
representation of original variables, for
discrimination purposes (Dillon et al., 1989;
Kamrunnahar et al., 2008). However, the proposed
work suggests that the dimensionality reduction
should take place on the original variable space
instead of the components, since it becomes more
obvious which original variables are really relevant.
The datasets from each subset of variables undergo
35
Dias N., Kamrunnahar M., Mendes P., Schiff S. and Correia J. (2009).
VARIABLE SUBSET SELECTION FOR BRAIN-COMPUTER INTERFACE - PCA-based Dimensionality Reduction and Feature Selection.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 35-40
DOI: 10.5220/0001533200350040
Copyright
c
SciTePress

linear discriminant analysis (LDA) for classification.
The best subset in discriminating between task
performances, for each subject, is evaluated by a
cross-validation error.
We evaluated the proposed VSS method through
both synthetic and real datasets. A synthetic dataset
enabled us to evaluate this method in a controlled
environment and simulated the 3 levels of variable
relevance mentioned above. The real datasets were
generated from movement-related potentials (MRP)
as EEG responses to movement imagery tasks
(Babiloni et al., 1999). Four subjects were submitted
to these experiments and no subject had previous
BCI experience. The lowest cross-validation error
for each subject and the corresponding number of
variables selected were assessed.
2 EXPERIMENTAL DESIGN
2.1 Symthetic Data
Among all variables p in the synthetic dataset, q
relevant and p-q irrelevant Gaussian distributed
variables were generated. All the generated variables
had the same standard deviation σ. In order to best
simulate a typical multivariate dataset, the relevant
features were generated in pairs with correlation
between variables. In this way, the variables are
more discriminative if considered together. The first
variable in each pair is considered as the
predominant variable since its mean has distance d
between groups. The distribution parameters were
set similarly to (Lai et al., 2006). Pairs of correlated
variables were generated until the quantity of
relevant variables is reached. The remaining p-q
variables (i.e. discrimination irrelevant) were
generated from the same Gaussian distribution (no
mean difference) for both groups. Four different
datasets were generated with 80 samples: p=79 and
q=6; p=79 and q=12; p=40 and q=6; p=40 and q=12.
The first 2 datasets were intended to simulate the
high dimensional/low sample size problem. The last
2 represent a lower high-dimensional space. The
standard deviation σ was set to 2.5 in all datasets.
The mean difference d was set to be equal to σ to
simulate group overlapping. The values of both
distribution parameters were set to best approximate
the real variables extracted from the EEG data
collected.
2.2 EEG Data
Four healthy human subjects, 25 to 32 years old,
three males and one female, were submitted to 1
session each of motor imagery. The experiments
were conducted under Institutional Review Board
(IRB) approval at Penn State University.
Each session had 4 runs of 40 trials each. Each
subject was instructed to perform one of 4 tasks in
each trial. The tasks were tongue, feet, left hand and
right hand movement imageries. The following 2
imagery task discrimination cases were considered
for VSS algorithm evaluation: tongue vs. feet; left
hand vs. right hand. After the first 2 s of each trial, a
cue warned the subject to be prepared and 1 s later, a
cue about the required mental task was presented to
the subject. The subject was instructed to perform
the task in the 4 s after the cue.
Data were acquired from 9 electrodes according to
the standard 10-20 system (F3, Fz, F4, C3, Cz, C4,
P3, Pz, P4). All electrodes were referenced to linked
earlobes. Data were digitized at 256 Hz and passed
through a 4th order 0.5-60 Hz band-pass filter. Each
channel’s raw EEG signal was epoched from the cue
time point (0 s) to 4 s after the cue. The epoch was
subdivided in 1 s time windows with no overlap (4
time windows). Each epoch was low-pass filtered at
4 Hz with an 8th order Chebyshev type I filter.
Then, the filtered 256 points time series was down
sampled to be 10 points long. The Matlab
“decimate” function was used to accomplish both
the filtering and down sampling. Only the 1
st
-8
th
data
points of the resultant time series form the feature
vector for each time window. The last 2 points of the
time series were discarded because they seemed to
be irrelevant on previous analyses. The feature
matrix of each time window had 72 variables (8
features from each of the 9 electrodes) and 80
samples.
3 VARIABLE SUBSET
SELECTION
The proposed VSS algorithm can be partitioned in 3
sequential procedures. Initially, the dataset
dimensionality is reduced through a formulation of
PCA that accommodates the group structure of the
dataset (Dillon, 1989). Once the number of variables
is reduced, the remaining variables are ranked
according to their discrimination ability. Finally a
cross-validation procedure is applied in order to
determine the optimum subset of variables to select.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
36

3.1 Dimensionality Reduction
The original feature matrix Y has samples in rows
(n) and variables (p) in columns (p < n-1). The PCs
are linear projections of the variables onto the
orthogonal directions that best describe the dataset
variance independent of any group structure that
might be present in the data. Initially, the p PCs in
U
n×p
are calculated through singular value
decomposition (SVD) of Y. Although the PCs are
already organized by decreasing order of total
variance accounted for, this order is optimized for
orthogonality rather than discrimination between
groups. In order to compensate for this and take the
data group structure into account, the components
should be ordered according to the across group
variance (AGV) score (Dias, 2007), instead of the
eigenvalues λ
i
order that account for the total
variance. The AGV score is used to rank each
component in terms of the between group variance
instead of the total variance. The AGV score is
calculated according to (1) and its implementation is
detailed in the appendix.
T
i Between i
i
i
vv
AGV
λ
Ψ
=
(1)
Ψ
Between
represents the between group covariance
matrix (see appendix for calculation details) and v
i
represents the i
th
eigenvector of Ψ.
The dimensionality reduction results from the
truncation of the component matrix (U), previously
ordered according to the AGV scores. The
truncation criterion was set to 80% (unless otherwise
noted) of the cumulative sum (in decreasing order of
the AGV scores) of every component’s AGV. The
truncated version of U (U
n×k
), with k < p
components, is a lower dimensional representation
of the original variable space in Y and is often used
as a reduced feature matrix (Kamrunnahar, 2008).
Although each component in U is a linear
combination of all the original variables in Y, it is
not always evident what each component means in
the original variable space (Jolliffe, 2002). Hence,
the original k variables (Y
n×k
) which have the most
variance accounted for in the truncated component
space (U
n×k
) are used as a representation of the
original variable space Y. The vector sub keeps the
indices of the k variables that were kept after this
dimensionality reduction (see appendix for details).
Therefore, at the end of this stage, the
dimensionality of the dataset has been reduced from
p to k.
3.2 Variable Ranking
On the one hand, 2 different variables might have
the same variance accounted for the k PCs but have
different importance as discriminators (predictor in
LDA). We indeed found in the current analyses, for
both synthetic and real BCI datasets, that variables
with high variance accounted for the k PCs were
poor discriminators. On the other hand, a variable
that is a good discriminator is expected to have high
variance in the k PCs that were kept in the previous
subsection. Therefore, in this 2
nd
procedure, a ranked
list of the variables in sub is calculated according to
their discrimination ability. The rank, in (2),
computes the multivariate distance penalization
observed when each variable at a time is removed
from the subset of k variables.
()
j
j
rank Y D D
−
=
−
, jsub∈
(2)
The multivariate distance D is calculated as in (3).
Μ
1
and Μ
2
are the multivariate means of groups 1
and 2 respectively, and Ψ
k
is the covariance matrix
of the k selected variables. D
-j
is calculated by
excluding the variable j to calculate the multivariate
distance.
1
2
12 12
()()
T
k
D
⎡
⎤
=Μ−Μ ΨΜ−Μ
⎣
⎦
(3)
The output of this procedure is the reorganized
version of sub with variables in descending order
according to rank(Y
j
).
In order to show the importance of the
dimensionality reduction step in eliminating non-
relevant variables, all the p variables in Y were
ranked and classified in a separate cross-validation
step where the 1
st
procedure (i.e. dimensionality
reduction) was omitted (figures 1 and 3).
3.3 Cross-Validation
Once the subset of variables sub is ordered
according to (2), an LDA classifier is applied
iteratively on each feature matrix Y
sub(f)
containing
the f top most ranked variables in sub, for f=1,…,k.
The leave-one-out error rate (LOOR) is calculated in
each iteration. The lowest LOOR value achieved
determines which subset of variables opt (opt ⊂ sub)
is optimal according to this approach (results in
figures 1 and 3).
A different approach of Fisher Discriminant
Analysis (Schiff, 2005) that was robust on
spatiotemporal EEG pattern discrimination was
applied. The canonical discrimination functions Z
i
are the result of a linear transformation of original
VARIABLE SUBSET SELECTION FOR BRAIN-COMPUTER INTERFACE - PCA-based Dimensionality Reduction and
Feature Selection
37
data Y according to (4). The discrimination
coefficients of each i
th
canonical discrimination
function are denoted by the columns of b
i
T
.
()
T
isubji
Z
Yb=
(4)
The group membership prediction was based on
the posterior probability π
gz
as the probability that
the data of a given value z came from group g
(Dias, 2007). The highest π
gz
value (g ∈ {1,2}: only
left vs. right hand movements and tongue protrusion
vs. feet movement imagery discriminations were
assessed) was the predicted group membership for
posterior calculations.
The discrimination quality was assessed by
LOOR and Wilks’ statistic W. Further details on the
classification method can be found in (Dias, 2007).
4 RESULTS
The feature selection process on the synthetic data
was evaluated for 4 different cases of number of
features p and different number of relevant features
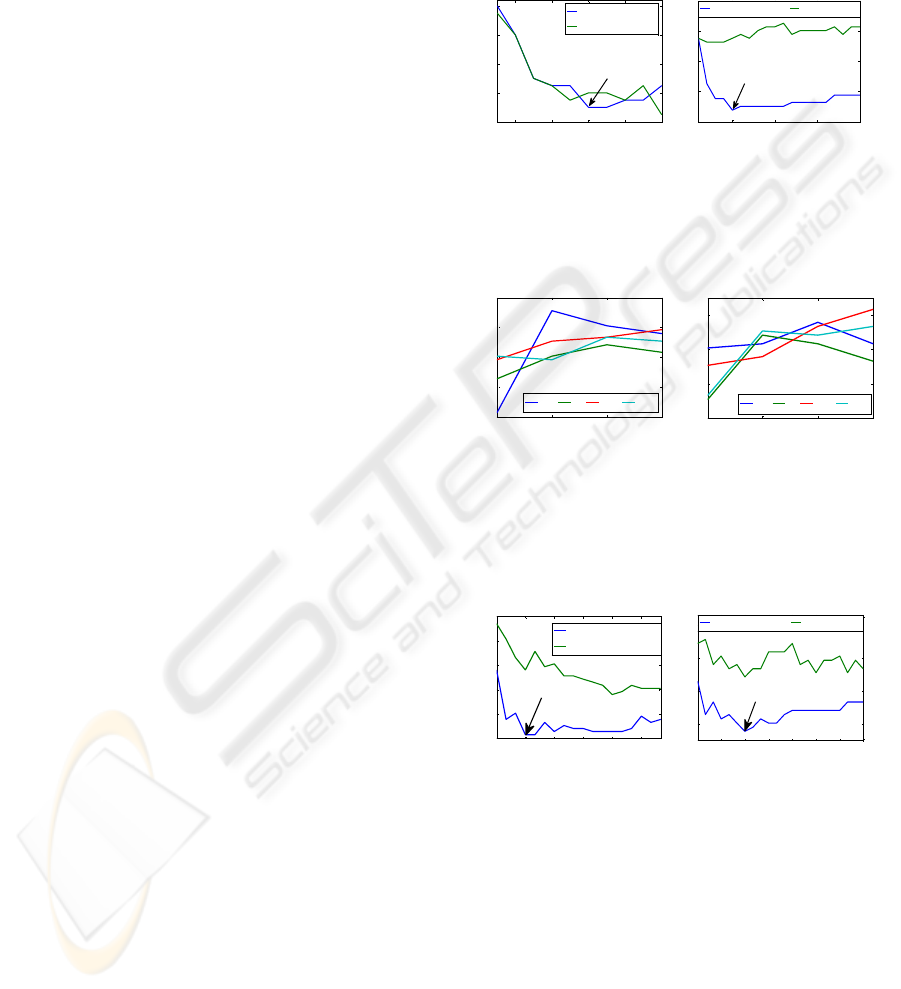
q. Two cases are illustrated in figure 1. The 1
st
case
(p=40; q=6) at figure 1 left plot achieved 7.5 % of
LOOR and Wilks’ statistic W=0.33 which is very
significant since the 99 % confidence value W99 (W
is chi-squared distributed with p×(n-1) degrees of
freedom) for this statistic is 0.74. All 6 relevant
variables were selected for the optimal subset
(minimum LOOR). The 2nd case (p=40; q=12)
achieved 0 % LOOR for 10 variables (10 relevant
features out of 12 were selected and all the
predominant ones were selected) and W=0.16
(W99=0.75). The 3rd case (p=79; q=6) at figure 1
right plot reached 3.7 % LOOR for 5 variables (all
the predominant variables were selected) and
W=0.23 (W99=0.83). Finally the 4th case (p=79;
q=12) reached 3.7% LOOR for 14 variables (all
relevant variables were selected plus 2 irrelevant
ones) and W=0.14 (W99=0.69).
The FSS algorithm was also tested in real data
from 4 subjects which achieved between 11.4 % and
29.1 % LOOR (each subject’s best time window) for
left vs. right imagery (figure 2 left plot). During
tongue vs. feet imagery performance, the LOOR was
between 15.2 % and 30.4 % (0-1 s time window), as
seen on figure 2. The best occurrence from each
discrimination case is depicted on figure 3. In both
cases 4 variables were selected as the optimal subset.
In JF’s left vs. right performance (figure 3 left plot)
analyses, features from C4, Pz, F3 and Fz channels
were selected. In JI’s tongue vs. feet performance
(figure 3 right plot) analyses, features from P3, C3,
Cz and Pz channels were selected. On figure 1 as
well as figure 3, the variables selected until the
minimum LOOR is reached (opt) are considered
relevant and all the following variables selected are
considered irrelevant.
2 4 6 8 1
0
0.05
0.1
0.15
0.2
0.25
#variables selected j
LOOR(%)
p=40 q=6
VSS steps 1+2
VSS step 2
opt
δ
=
85%
5 10 15 20
0
0.1
0.2
0.3
0.4
#variables selected j
LOOR(%)
p=79 q=6
VSS steps 1+2 VSS step 2
opt
Figure 1: Plots of LOOR vs. number of variables selected
from sub for both the VSS algorithm (blue line) and VSS
2nd step separately (green line). Two different cases were
illustrated for q relevant variables out of p variables.
1 2 3 44
0.1
0.2
0.3
0.4
0.5
window last time point (s)
LOOR(%)
left vs. right performance
JF JI JM SS
1 2 3 4
0.1
0.2
0.3
0.4
window last time
p
oint
(
s
)
LOOR(%)
tongue vs. feet performance
JF JI JM SS
Figure 2: LOOR variation through 4 time windows (1-4 s
after cue) for all 4 subjects (JF, JI, JM and SS) for left vs.
right movement imagery performance (left plot) and
tongue vs. feet movement imagery performance (right
plot).
1 4 7 10 13 16 1
8
1
8
0,1
0,3
0,5
#variables selected j
LOOR(%)
JF left vs. right (window 0-1 s)
VSS steps 1+2
VSS step 2
opt
1 4 7 10 13 16 19 22
0.2
0.3
0.4
0.5
#variables selected j
LOOR(%)
JI tongue vs. feet (window 0-1 s)
VSS steps 1+2 VSS step 2
opt
Figure 3: LOOR vs. number of variables selected for JF
(left plot) and JI (right plot) in time window 1.
5 DISCUSSION
AND CONCLUSIONS
The goal of this VSS approach is to find few
relevant variables for discrimination in a high-
dimensional variable space. The results with
synthetic datasets reveal that this goal is feasible: at
least 83% of the relevant variables were selected for
the optimal subsets; 100% of the predominant
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
38

variables were selected for all optimal subsets; all
the discriminations reached less than 7.5% LOOR
and were very significant. The 1
st
and 2
nd
cases show
that this approach is also applicable for lower
dimensional variable spaces (p=40;N=80) as well as
high-dimensional ones (3
rd
and 4
th
cases). As shown
in figure 1 for p=79 and figure 3 the LOOR is much
larger when only the 2
nd
step of VSS is applied alone
(green line) to all original variables, than the LOOR
achieved when both steps are applied jointly (blue
line). Although the LOOR increase in the absence of
the 1
st
step is less evident for p=40 (figure 1), the
optimal solution is still achieved when both steps are
applied jointly. Therefore, it can be concluded from
these results that the proposed algorithm reduces the
number of variables efficiently as well as decreases
the discrimination error.
Real BCI data results, on figure 2, show three
good discrimination cases (LOOR lower than 16%)
for three different subjects. The presence of just few
relevant variables in these BCI datasets seems likely
once 4 (subject JF) and 7 (subject JI) variables out of
72 were selected for the optimal subset in figure 3.
As suggested in the literature (Babiloni, 1999), for
all cases but one in figure 2, the best time window
for classification appears to be the first second after
cue.
Our findings show a novel mean to down-select
variables in BCI that accomplishes both
discriminative power and dimensionality reduction.
Such a strategy is valuable in decreasing the
computational complexity of neural prosthetic
applications.
ACKNOWLEDGEMENTS
N. S. Dias is supported by the Portuguese
Foundation for Science and Technology under Grant
SFRH/BD/21529/2005 and Center Algoritmi. S. J.
Schiff and M. Kamrunnahar were supported by a
Keystone Innovation Zone Grant from the
Commonwealth of Pennsylvania, and S. J. Schiff by
NIH grant K02MH01493.
REFERENCES
Babiloni, C., Carducci, F., Cincotti, F., Rossini, P.M.,
Neuper, C., Pfurtscheller G., Babiloni, F., 1999.
Human movement-related potentials vs
desynchronization of EEG alpha rhythm: A high-
resolution EEG study. In NeuroImage, vol. 10, pp.
658-665.
Dias, N.S., Kamrunnahar, M., Mendes, P.M., Schiff, S.J.,
Correia, J.H. Customized Linear Discriminant
Analysis for Brain-Computer Interfaces. In Proc.
CNE '07 IEEE/EMBS 2-5 May 2007, pp. 430-433.
Dias, N.S., Kamrunnahar, M., Mendes, P.M., Schiff, S.J.,
Correia, J.H. Comparison of EEG Pattern
Classification Methods for Brain-Computer Interfaces.
In Proc.29th EMBC 22-26 Aug 2007, pp.2540-2543.
Dillon, W.R., Mulani, N., Frederick, D.G., 1989. On the
Use of Component Scores in the Presence of Group
Structure. JOURNAL OF CONSUMER RESEARCH,
vol. 16, pp. 106-112.
Duda, R.O., Hart, P.E., Stork, D.G., 2000. Pattern
Classification. Wiley.
John, G.H., Kohavi, R., Pfleger, K., 1994. Irrelevant
Features and the Subset Selection Problem. In Proc.
11th Int. Conf. Machine Learning, 121-129.
Jolliffe, I.T., 2002. Principal Component Analysis,
Springer 2
nd
edition.
Kamrunnahar, M., Dias, N.S., Schiff, S.J. Model-based
Responses and Features in Brain Computer Interfaces.
In Proc. 30
th
IEEE EMBC 20-25 Aug 2008, pp.4482-
4485.
Lai, C., Reinders, M.J.T., Wessels, L., 2006. Random
subspace method for multivariate feature selection.
Pattern Recognition Letters, no.27, pp.1067-1076.
Schiff, S.J., Sauer, T., Kumar, R., Weinstein, S.L., 2005.
Neuronal spatiotemporal pattern discrimination: The
dynamical evolution of seizures. NEUROIMAGE, 28
ed, pp. 1043-1055.
Wolpaw, J.R., McFarland, D.J., Vaughan, T.M., 2000.
Brain–Computer Interface Research at the Wadsworth
Center. IEEE TRANSACTIONS ON REHAB.
ENGINEERING, vol. 8, no. 2, pp. 222-226.
Yu, L., Liu, H., 2004. Efficient feature Selection via
Analysis of Relevance and Redundancy. Journal of
Machine Learning, no. 5, pp. 1205-1224.
APPENDIX
This section details the dimensionality reduction
implemented on the proposed variable selection
algorithm. The algorithm presented on the bottom of
this section enumerates every command of this
procedure.
On the line 1 of the algorithm, Y is decomposed
through SVD into 3 matrices: U
n×p
(component
orthogonal matrix), S
p×p
(singular value diagonal
matrix) and V
p×p
(eigenvector orthogonal matrix).
The eigenvalues vector
λ
is calculated on line 2 as
the diagonal of S
2
. The AGV score is calculated for
every PC through lines 4 to 6.
Once it is considered that both groups to
discriminate have the same covariance matrix, the
pooled covariance matrix should be calculated as the
within group covariance matrix Ψ
Within
:
VARIABLE SUBSET SELECTION FOR BRAIN-COMPUTER INTERFACE - PCA-based Dimensionality Reduction and
Feature Selection
39

112 212
(1) ( 1) 2
Within
nnnnΨ=−Ψ+−Ψ−−
Ψ
i
and n
i
are respectively the covariance matrix and
number of samples belonging to the i
th
group.
Considering Ψ as the total covariance matrix, the
between groups covariance matrix Ψ
Between
is
calculated as:
B
etween Within
Ψ=Ψ−Ψ
On line 7, the vector rAGV is a version of AGV
in descending order. On lines 8 and 9,
λ
and the
columns of V are similarly reordered in r
λ
and rV
respectively, to match rAGV. Note that AGV is
originally ordered according to the descending order
of the eigenvalues
λ
i
(line 5). The reordered AGV
indices are kept in dpc, which stands for
‘discriminative PCs’, where rAGV=AGV
dpc
.
Each component’s percentage of the sum of all
AGV scores is calculated on line 10. The number of
components k out of p to maintain determines the
truncation to be performed in U. k is calculated on
line 11 as the number of elements of %rAGV whose
cumulative sum is higher than the component
selection criterion (δ).
Considering the spectral decomposition
property of the covariance matrix:
1
p
T
iii
i
vv
λ
=
Ψ=
∑
The columns of V are the eigenvectors v
i
. The
diagonal values of Ψ give the variance of the
variables in Y accounted for the p PCs, as well as
TruncVar
j
gives the ‘truncated’ variance of variable j
accounted for the k PCs that were kept for
dimensionality reduction.
On lines 15 and 16, the vector rTruncVar is a
descending ordered version of TruncVar and the
indices of the k top most variables in rTruncVar are
copied into the subset of variables sub.
Input Data: Y, Ψ
BETWEEN
, δ
Output Data: sub
1. [U,S,V
T
] = SVD(Y);
2. λ = diag(S
2
);
3. p = # columns of Y;
4. for i=1 to p do
5. AGV
i
= V
i
T
×Ψ
BETWEEN
×V
i
/λ
i
6. end for
7. [rAGV,dpc] = sort AGV in
descending order
8. rλ = λ
dpc
{λ is reordered to
match rAGV}
9. rV = V
dpc
{V is reordered to
match rAGV}
10. %rAGV = 100*rAGV / Σ
i=1,..,p
rAGV
i
11. k = number of first %rAGV
elements whose cumulative sum > δ
12. for j=1 to p do
13. TruncVar
j
= Σ
i=1,..,k
rλ
i
×rV
ji
2
14. end for
15. [rTruncVar,Index] = sort
TruncVar in descending order
16. sub = 1st k elements in Index
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
40
