A WAY FOR PREDICTING AND MANAGING THE GLYCAEMIC
INSTABILITY OF THE DIABETIC PATIENT
Farida Benmakrouha, Christiane Hespel
IRISA-INSA,20 Avenue des Buttes de Coesmes, 35043 Rennes cedex, France
Mikhail V. Foursov
IRISA-Universite de Rennes-1, 35042 Rennes cedex, France
Jean-Pierre Hespel
Centre Hospitalier Universitaire de Rennes, 35000 Rennes, France
Keywords:
Dynamical system, Bilinear model, Regulation, Stability, Insulin perfusion.
Abstract:
We study the Bounded-Input-Bounded-Output (BIBO) stability of the system modeling the behavior “insulin
delivery/glycaemia” of the diabetic patient, under continuous insulin infusion, continuous glucose monitoring,
in order to point out that the patient is entering in a period of stable/unstable equilibrium.
The model is a bilinear dynamical system predicting for an interval of 15 minutes, with an average error of
15%. In case of stable equilibrium, the prediction will be valid for a longer time interval, when in case of
unstable equilibrium, it will leads one to reduce the time intervals.
The BIBO stability is studied by computing the generating series G of the model. This series, generalization
of the transfer fuction, is a tool for analyzing the stability of bilinear systems. It is a rational power series in
noncommutative variables and by evaluating it, a formal expression of the output in form of iterated integrals
is provided. Three cases arise: firstly, the output can be explicitly computed; secondly, the output can be
bounded/unbounded if the input is bounded; thirdly, no conclusion seems available about the BIBO stability
by using G. We propose a stabilizing constant input η by studying the univariate series G
η
.
1 INTRODUCTION
Among the different medical possibilities to adminis-
ter insulin, the sub-cutaneous route is most secure and
easy to implement, but it lacks reliability. The intra-
venous route is the most rapidly responding method,
but it may cause vascular complications. The in-
traperitoneal route seems to be the most physiological
one.
In order to carry out a glycaemic regulation by an in-
traperitonal infusion of insulin, it is necessary to pre-
dict the glycaemia as a function of the insulin infu-
sion rate, for a given patient and a given insulin. The
first closed-loop regulation method was developed by
A. Albisser back in 1974 (A. M. Albisser, ). Among
other methods, we can mention (J. L. Selam, 1992).
But, in spite of many positive aspects of these meth-
ods, none of them was unanimously accepted by the
medical community. This is partly due to insufficient
frequency of glycaemic sampling and the difficulty to
vary rapidly the insulin infusion rates.
Recent technical progress made it possible to over-
come these difficulties. In 2000 appeared the first
holter glycaemic device: the CGMS (Continuous
Glucose Monitoring System) which allows one to
measure the glycaemia every 3 minutes. A first reg-
ulation system based on the CGMS was developed in
2001 by E. Renard of CHU of Montpellier in collab-
oration with Medtronic Minimed (Renard, 2003). In
2006, E. Renard (E. Renard, 2006), analyzes the im-
plantation of three components: a pump for peritoneal
insulin delivery, a central intravenous glucose sensor
and a controller. Meals are preceded by a handheld
programmed bolus calculed for pre-meals. A prob-
lem remains in case of unstability of the glycaemia
close to a meal, a stress, a physical effort.
335
Benmakrouha F., Hespel C., Foursov M. and Hespel J. (2009).
A WAY FOR PREDICTING AND MANAGING THE GLYCAEMIC INSTABILITY OF THE DIABETIC PATIENT.
In Proceedings of the International Conference on Biomedical Electronics and Devices, pages 335-338
DOI: 10.5220/0001121003350338
Copyright
c
 SciTePress

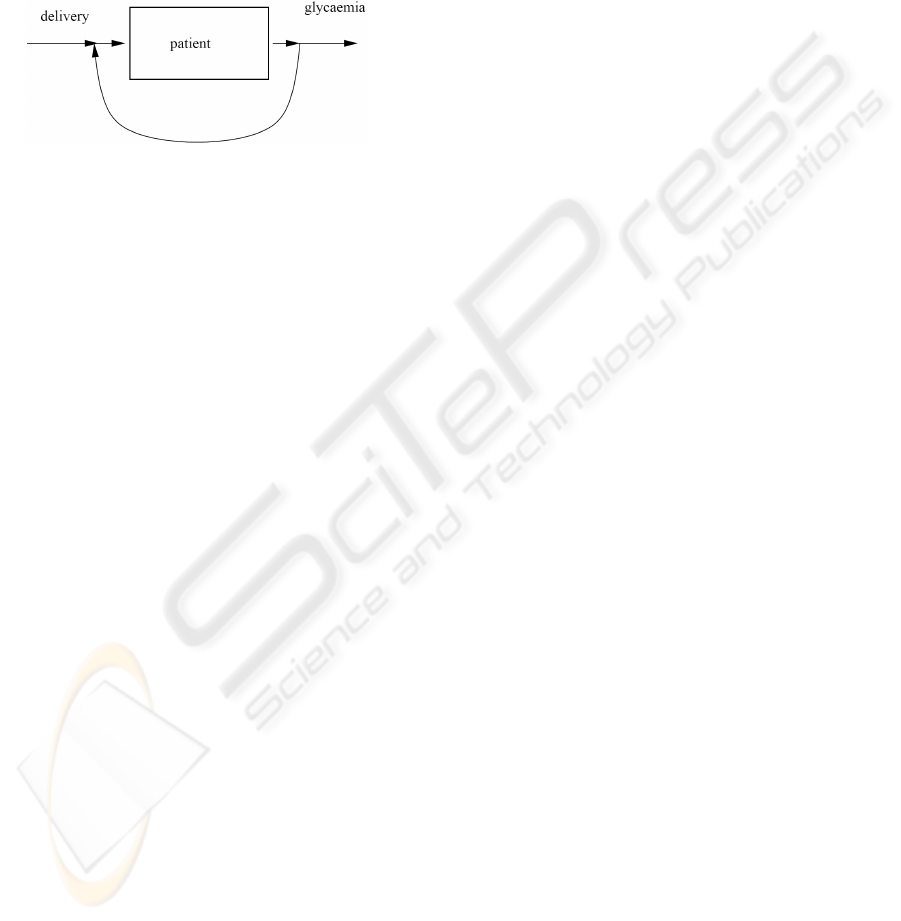
Then we proposed a bilinear modeling giving a
good approximation of the behavior “insulin deliv-
ery/glycaemia” on an interval of 15 minutes, in stan-
dard conditions (C. Hespel, 2000).
Once the model is known, the regulation consists
in inverting the input/output behavior of the system
(M. V. Foursov, 2003; M. V. Foursov, 2004). One has
to calculate the input in terms of the output function
one wishes to obtain (Fig.1). This regulation is par-
Figure 1: Regulation.
tially closed-loop because the glycaemic values are
only used every 15 minutes in order to compute the in-
sulin delivery. On constant intervals of time [t
i
,t
i+1
]
i
,
we compute some model M
i
and function insulin de-
livery u
i
(t) in order to follow an ideal trajectory y
i
(t)
for the glycaemia. On every time interval, the trajec-
tory is recalculed because of the variation between the
ideal trajectory and the true trajectory.
The crucial point consists in determining the size of
the time intervals, i.e. the frequency of the changes of
the insulin delivery. The study of the stability leads
us to reduce the size of the interval when the system
is unstable.
2 PRELIMINARIES: MODELING,
REGULATION
Two techniques are used to achieve this goal:
Phenomenological modeling requires a knowledge of
the equations governing the evolution of the process.
Such models of the glycaemic behavior of diabetics
were developed (Albisser, ).
In the behavioral modeling, the system is regarded as
a black box (J. Sjoberg, 1995). The goal is to con-
struct a model that approximates the system with a
desired precision (Chen and Chen, ). The parame-
ters involved in the obtained system of equations have
no practical significance, but their number depends on
the required precision.
A commonly-used class of models is formed by linear
dynamical systems. Linear-model-based regulation is
simple to implement and it gives quite satisfactory re-
sults in many cases. It did not seem to be sufficient
for regulating the glycaemia of diabetics.
Another class of models consists of bilinear systems.
A bilinear system is quite similar to a linear one: it is
additionally linear as a function of the input. One has
thus more leeway to approximate the real system with
a better precision. We choose to model the system by
a bilinear system whose dimension is not fixed.
Since a diabetic does not respond in the same way to
equal doses of insulin at different times of the day, we
suppose that she is described by different systems at
different time instants. So we construct a collection
of models that describe the behavior of the glycaemia
under certain conditions. Each model is thus valid
only for a certain period of time (at least 15 minutes).
Mathematically, the problem is to identify locally
(near t
0
) up to a given order k, a single input sys-
tem with drift considered as a black box, when only a
sample of the input/output data is known. Our method
involves the identification up to order k of the gener-
ating series G of the unknown system and the con-
struction of a bilinear system (B
k
) approximating the
unknown system up to k.
An advantage of this method is the possibility to pro-
vide, in terms of the order k, a system (B
k
) approxi-
mating the unknown system. (B
k
) is chosen so that its
output and the output of the unknown system coincide
up to k. The problem of identification of dynamical
systems in a neighborhood of t
0
is the following: to
determine the generating series of the unknown sys-
tem, up to a given order k, given the Taylor series of
the input and corresponding output functions.
The identification involves the following 3 steps. Dur-
ing the first step, one obtains a system of linear equa-
tions that express the relationship between the deriva-
tives of the input and the output. The unknown pa-
rameters are certain linear combinations of the coeffi-
cients of the generating series. On the next step, these
linear combinations of the coefficients are identified
from the available data, by choosing appropriate in-
put/output sets. Finally, the coefficients are identified
by solving another system of linear equations.
A bilinear system corresponding to a rational series of
minimal rank is constructed providing a local model.
2.1 The Bilinear Model
A bilinear system (B) with a single input u
1
(t) and a
drift u
0
(t) ≡ 1 is given by its state equations
(B)

x
(1)
(t) = (M
0
+ u
1
(t)M
1
)x(t)
y(t) = λ.x(t)
(1)
x(t) ∈ an R−vector space Q, M
0
, M
1
, λ are R−linear.
We consider the alphabet Z = {z
0
, z
1
}, where z
0
codes
the drift and z
1
codes the input. The expansion of the
generating series G built on Z, by noting w a word
∈ Z
∗
, is G =
∑
w∈Z
∗
hG|wiw.
BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices
336

G is a rational series defined from (1) by:
G = λ.x(0) +
∑
ν≥0
1
∑
j
0
,···, j
ν
=0
λ.M
j
0
·· ·M
j
ν
x(0)z
j
0
·· ·z
j
ν
(2)
We compute the rational expression associated with
(2), by generalizing the Schutzenberger’s method
(Schutzenberger, 1961).
By “evaluating” the expression of G, we obtain a for-
mal expression of the output (Fliess, 1981)
y(t) =
∑
w∈Z
∗
hG|wi
Z
t
0
δ(w) =
Z
t
0
δ(G) = ε(G) (3)
where the iterated integrals are recursively defined by:
Z
t
0
δ(w) =

1 i f w = 1
Z
R
t
0
(
R
τ
0
δv)u
i
(τ)dτ i f w = vz
i
(4)
And we compute the iterated integral
R
t
0
δ(G).
2.2 The Regulation Method
Once the model is known, the regulation consists in
inverting the input/output behavior. One has to cal-
culate the input in terms of the output function one
wishes to obtain. This regulation is partially closed-
loop, since the glycaemic values are used to recalcu-
late the insulin infusion rates every 15 minutes.
In a previous paper (M. V. Foursov, 2002) we have
shown that we are capable of finding the Taylor se-
ries expansion of the command from the Taylor series
expansion of the desired output trajectory, using gen-
erating series techniques similar to those used during
the identification and the modeling. The algorithm
consists in sequential solving a system of polynomial
equations. If the model of a diabetic were an ex-
act one, this would be sufficient to regulate the gly-
caemia. But since our bilinear model is an approxi-
mation of the actual one, the glycaemic behavior will
eventually deviate from the chosen trajectory. Then,
the trajectory has to be recalculated in order to com-
pensate for these deviations and the insulin infusion
device has to be reprogrammed accordingly.
An important point is to determine the frequency of
change of the insulin infusion rates. The first tests of
our modeling method (C. Hespel, 2000) showed that
we can predict the glycaemia over 15-minute inter-
vals with an error of about 10% or 15%. We need to
provide a new data to the pump every 15 minutes.
3 STUDY OF THE BIBO
STABILITY
A dynamical system is Bounded-Input-Bounded-
Output (BIBO) stable if its output y(t) is defined and
bounded for every bounded input u(t).
The output of a bilinear dynamical system can be
computed in evaluating its generating series. This
evaluation consists in integrating every term of this
series and in summing. We use the theorem of Hoang
(Hoang, 1990) :
Theorem 1. ∀k, let us suppose that G
k
is exchange-
able and let us denote ε(G
k
) by g
k
(ξ(t))
g
k
(ξ(t)) = g
k
(t, ξ
1
(t), ··· , ξ
m
(t)) (5)
where ξ
j
(t) is the primitive of the input u
j
(t) can-
celling for t = 0. Then, ∀k, the series
S
k
= G
0
z
i
1
G
1
·· · z
i
k
G
k
(6)
where z
i
1
, · · · , z
i
k
∈ Z, has the following evaluation:
ε(S
k
) = y(t) =
R
t
0
R
τ
k
0
·· ·
R
τ
2
0
g
0
(ξ(τ
1
))g
1
(ξ(τ
2
) − ξ(τ
1
))· · ·
g
k
(ξ(t)− ξ(τ
k
))dξ
z
i
1
(τ
1
)· · · dξ
z
i
k
(τ
k
)
(7)
Three cases occur: In some cases, this process is easy
and y(t) can be explicitly computed. In other cases, if
we assume that u(t) is bounded by 2 values Min, Max,
then we can know if so is y(t), without computing
explicitly y(t). Lastly, in some difficult cases, we only
try to find some stabilizant constant inputs u(t) = η
such that the output remains bounded, if it is possible.
We prove that the output of the bilinear system for the
input u(t) = η consists in evaluating some univariate
series G
η
. This series being rational, can be written
as a quotient of 2 polynomials. We can then use 2
propositions (F. Benmakrouha, 2007) dealing with the
poles of G
η
in order to decide that a stability exists for
u(t) = η
Proposition 1. A necessary condition for the BIBO
stability of (B), is that, for every η ∈ R, the real part
of the poles of G
η
is ≤ 0 and the imaginary poles of
G
η
are single.
Proposition 2. If there exists η such that every pole
of G
η
has a negative real part and if every imaginary
pole is single, then u(t) = η is a stabilizing input
3.1 Example 1
For an insulin delivery u(t), a glycaemia y(t), the state
equations of the system (B
2
) are



x
(1)
(t) = (

0 0
a b

+ u(t)

0 0
1 0

)x(t)
y(t) = (1.5 1) x(t)
(8)
The generating series is :
G
2
= (z
1
+ az
0
)(bz
0
)
∗
+ 1.5 (9)
G
2
= G
21
+ G
22
+ 1.5 and y(t) = ε(G
2
)
with G
21
= z
1
(bz
0
)
∗
, G
22
= az
0
(bz
0
)
∗
A WAY FOR PREDICTING AND MANAGING THE GLYCAEMIC INSTABILITY OF THE DIABETIC PATIENT
337

We obtain an explicit expression of y(t):
ε(G
21
) = e
bt
R
t
0
e
−bτ
1
dξ
1
(τ
1
)
ε(G
22
) = ae
bt
Z
t
0
e
−bτ
1
dτ
1
(10)
For u(t) = η then ξ
1
(τ
1
) = ητ
1
, we get :
y
2,η
(t) =
η+a
b
(e
bt
− 1) + x(0)
This system is not BIBO for b > 0.
This system is BIBO for b < 0 (if M
1
≤ u(t) ≤ M
2
then y(t) is bounded)
For instance, for a > 0, b < 0, 0 ≤ u(t) ≤ M, then
y(t) ≤ x(0) +
M+a
−b
3.2 Example 2
The state equations of the bilinear system (B
3
) are

























x
(1)
(t) = (


0 0 0
a b c
0 a 0


+u(t)


0 0 0
1 0 0
0 1 0


)x(t)
y(t) = (1.5 1 0) x(t)
(11)
The generating series is
G
3
= (z
1
+ az
0
)(bz
0
+ (z
1
+ az
0
)cz
0
)
∗
+ 1.5 (12)
We compute G
3,η
by substituting ηz
0
to z
1
in G
3
:
G
3,η
= 1.5 +
(a+η)z
0
1−bz
0
−(a+η)cz
2
0
.
If η 6= −a then we decompose G
3,η
in partial fractions
for studying the constant stabilizing inputs
u(t) = η depending on the parameters a, b, c.
4 CONCLUSIONS AND FUTURE
WORKS
The BIBO stability of a bilinear system cannot be
generally studied by considering its state equation. In
this paper, we use the “evaluation” of its generating
series G. If the rational expression of G is simple or
obtained by concatenating some simple rational ex-
pressions, then the use of the generating series of the
system provides an answer about the stability and a
bound for the output. Otherwise, we can look for a
stabilizant constant input u(t) = η by using the uni-
variate series G
η
.
By applying this method to the bilinear model approx-
imating the behavior “insulin delivery/glycaemia”,
we expect an information about the stability of the
system describing really this behavior.
A specific surveillance depending on whether the sys-
tem is stable/unstable will be set. Rather than take
constant interval of 15 minutes for recalculate the
ideal trajectory of the glycaemia, we propose that the
time intervals depend on this information about the
stability. In case of unstability, the varying size of the
intervals of time would be defined in order to keep the
glycaemia between some moderate bounds.
REFERENCES
A. M. Albisser, B. S. Leibel, T. G. E. e. a. An artificial
endocrine pancreas. Diabetes, 23:389–396.
Albisser, A. M. Intelligent instrumentation in diabetes man-
agement. CRC Crit. Rev. Biomed. Eng., 17:1–24.
C. Hespel, J. P. Hespel, E. M. G. J. G. F. B. (2000). Al-
gebraic identification: Application to insulin infusion.
ISGIID’2000 Evian.
Chen, T. and Chen, H. IEEE T.Neur.Net.
E. Renard, G. Costalat, H. C. J. B. (2006). Artifi-
cial beta-cell: clinical experience toward an im-
plantable closed-loop insulin delivery system. Dia-
betes Metabolism, pages 497–502.
F. Benmakrouha, C. H. (2007). Generating formal power
series and stability of bilinear systems. 8th Hellenic
European Conference on Computer Mathematics and
its Applications (HERCMA 2007).
Fliess, M. (1981). Fonctionnelles causales non lin
´
eaires et
ind
´
etermin
´
ees non commutatives. Bull . Soc . Math.
France, 109:3–40.
Hoang, N. M. (1990). Contribution au d
´
eveloppement
d’outils informatiques pour r
´
esoudre des probl
`
emes
d’automatique non lin
´
eaire. Master’s thesis, Univer-
sit
´
e de LilleI.
J. L. Selam, P. Micossi, F. L. D. e. a. (1992). Clinical trial
of programmable implantable insulin pump for type i
diabetes. Diabetes Care, 15:877–885.
J. Sjoberg, Q. Zhang, L. L. e. a. (1995). Nonlinear
black-box modeling in system identification: a unified
overview. Automatica, 31:1691–1724.
M. V. Foursov, C. H. (2002). On formal invertibility of the
input/output behavior of dynamical systems. preprint
IRISA, 1439.
M. V. Foursov, C. H. (2003). On algebraic modeling and
regulation of the behavior of diabetics. Innovative
Technologies for Insulin Delivery and Glucose Sens-
ing.
M. V. Foursov, C. Hespel, D. B. J. H. (2004). Nouvelle
m
´
ethode de mod
´
elisation alg
´
ebrique et de r
´
egulation
de la glyc
´
emie. Infu-Syst
`
emes 21, 3:22–24.
Renard, E. (2003). Closed-loop system with implantable
pump and iv sensor. proceedings of the symposium
”Looking to the future”, pages 78–79.
Schutzenberger, M. P. (1961). On the definition of a family
of automata. Inform. Contr., 4:245–270.
BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices
338