IMPROVING ENERGY CONSUMPTION IN LARGE SCALE

WIRELESS SENSOR NETWORKS WITH MULTIPLE MOBILE

SINKS DEPLOYMENT

Ines Slama, Badii Jouaber and Djamal Zeghlache

Wireless Networks and Multimedia Services Department, Institut National des Télécommunications

9, rue Charles Fourier - 91011 Evry, France

Keywords: Large-Scale Wireless Sensor Networks, multiple sinks, design parameters, energy efficiency, graph

partitioning.

Abstract: In this paper, we consider the multiple sinks placement problem in energy constrained large-scale Wireless

Sensor Networks (WSN). First, some fundamental design parameters in WSNs such as nodes deployment,

the network architecture, sink velocity and transmission range, are investigated. Each of these parameters is

analysed and discussed according to its influence on the energy consumption in a WSN. Second, a simple

and efficient approach for the placement of multiple sinks within large-scale WSNs is proposed. The

objective is to determine optimal sinks’ positions that maximize the network lifetime by reducing energy

consumption related to data transmissions from sensor nodes to different sinks. Balanced graph partitioning

techniques are used to split the entire WSN into connected sub-networks. Smaller sub-networks are created,

having similar characteristics and where energy consumption can be optimized independently but in the

same way. Therefore, different approaches and mechanisms that enhance the network lifetime in small-size

WSN can be deployed inside each sub-network. Performance results show that the proposed technique

significantly enhances the network lifetime.

1 INTRODUCTION

A stationary sensor network is a static ad hoc

network composed of hundreds or thousands of

sensor nodes. Each sensor node is equipped with a

sensing device, a low computational capacity

processor, a short-range wireless transmitter-receiver

and a limited battery-supplied energy. Sensors

monitor some surrounding environmental

phenomenon, process the sensed data and forward it

towards a “close” a sink. This latter collects the data

from the different sensor nodes and transmits this

data to some remote control station where the data

will be exploited at the application level.

Achieving maximum lifetime in stationary

WSNs by optimally using the energy within sensor

nodes has been the subject of significant researches

in the last recent years. In this field, radio

transmission and reception operations are being

identified as the most energy consuming features.

On the other hand, the development of large-

scale sensor networks has drawn a lot of attention.

One of the main challenges is to set up new

architectures and mechanisms that can efficiently

scale up with the growing number of nodes that may

be required to ensure adequate coverage of large

areas of interest. At the same time, these new

architectures and mechanisms should maintain low

energy consumption per node so as to get by with

energy guaranty acceptable network lifetime.

Most of known existing protocols and

mechanisms are not scalable. They are mostly

conceived and adapted to relatively small networks

(i.e. reduced number of nodes) and/or when the

amount of data being gathered and transmitted is

small. In particular, centralised approaches, where

data from each sensor is sent to a central base

station, are not efficient and can not scale for large

wireless sensor networks.

The use of multiple mobile base stations is one

possible solution for large-scale WSNs. The idea is

to shorten the path (distance) between each sensor

node and the nearest base station, leading to save

energy consumption for transmission operations. To

achieve this efficiency, the multiple base stations

should be optimally placed within the sensed area.

Slama I., Jouaber B. and Zeghlache D. (2008).

IMPROVING ENERGY CONSUMPTION IN LARGE SCALE WIRELESS SENSOR NETWORKS WITH MULTIPLE MOBILE SINKS DEPLOYMENT.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 29-37

DOI: 10.5220/0002024700290037

 SciTePress

Our contributions in this paper include:

1. We present an interesting analysis of the

fundamental design parameters in large scale WSNs

with multiple, mobile sinks. A brief related work of

the existing techniques of multiple sinks deployment

in WSNs is also provided.

2. We propose to use graph theory techniques and in

particular graph partitioning in order to determine a

balanced partition of large-scale WSNs and then to

optimize the placement of the different sinks over

the obtained smaller sub-networks to minimize the

energy consumed for data transmissions.

The remaining of this paper is organized as

follows:

After discussing the design parameters analysis

and related work in section 2, the proposed scheme

is described and explained in section 3. Simulations,

performance results and analysis are presented and

discussed in section 4. Finally, concluding remarks

are given in section 5.

2 DESIGN PARAMETERS IN

ENERGY CONSTRAINED

WSNS: DESCRIPTION AND

RELATED WORK

In the following, we propose to discuss and analyse

some fundamental techniques and parameters that

should be seriously taken into account when

designing WSNs. We show through the analysis

presented below how important is their impact and

influence on the performance of such networks and

the way they should be investigated to face the

energy consumption challenge in WSNs.

2.1 Network Architecture for WSNs

Scalability of methods, algorithms and protocols

used in WSNs mostly depends on the

interconnection topologies of sensor nodes. Two

main architectures are proposed and studied in the

literature: Hierarchical and Flat topologies.

Hierarchical topologies allow easier scalable

mechanisms. A hierarchical (multi-tiered)

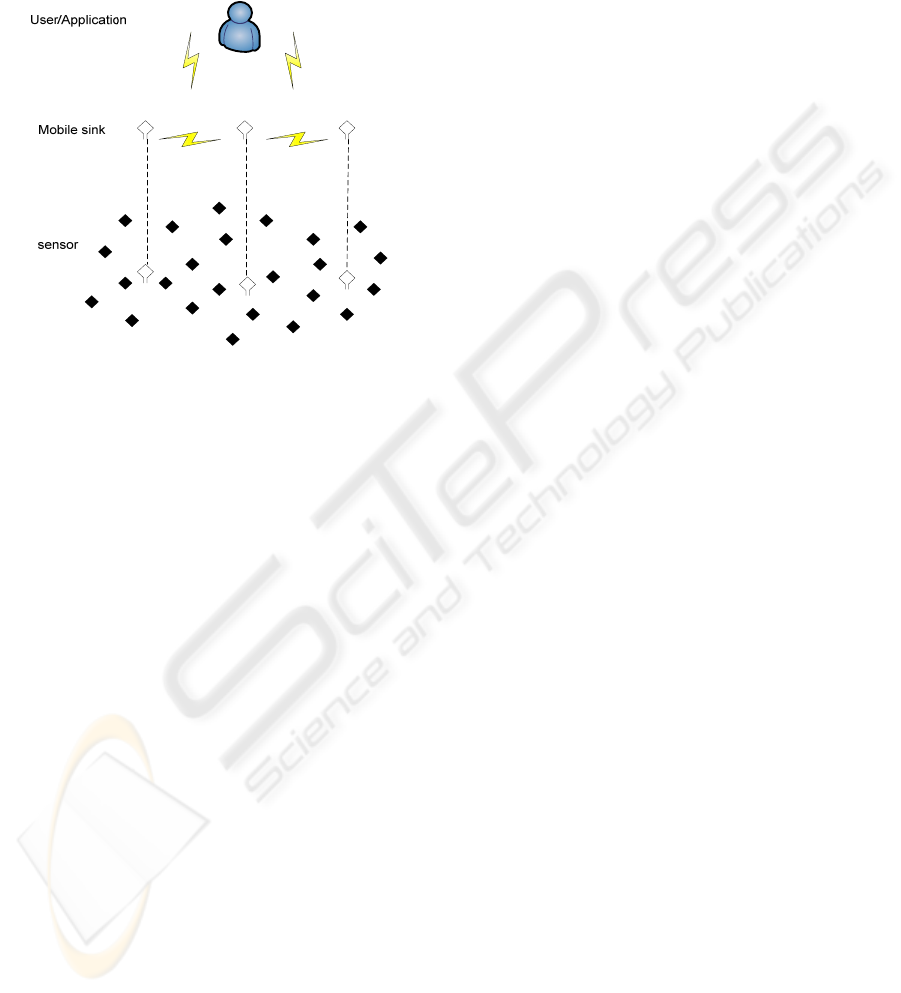
architecture comprising multiple tiers is depicted in

fig.1:

• The lowest tier: represented by a dense

deployment of low cost and low power static

sensor devices. Each sensor is equipped with a

micro controller, a flash memory and a radio.

Their main task is to collect information about

specific phenomena and send it to a higher tier.

• The middle tier: formed by mobile sinks which

have significant computation, memory and

storage resources and no power constraints.

These mobile sinks act as relays for information

gathering.

• The highest tier: it is the application which

queries the sensor network through a query

interface and the final information fusion point

that provides to the manager the data in interest.

Another example of hierarchical topologies is the

clustered two tier architecture where a single cluster

head handles several member nodes in its

neighbourhood (i.e. its cluster). The cluster heads

form a separate top layer communication structure.

Network protocols designed for these architectures

are highly scalable. However, they require the

definition of specific roles and mechanisms for

cluster heads as well as specific signalling

mechanisms.

As opposed to these hierarchical topologies, flat

distributed topologies are easier to deploy but more

difficult to scale. Here, nodes are connected in a

complete ad-hoc fashion. All sensing nodes have

equivalent roles with no specific hierarchy between

them. The main advantages of flat topologies are

their easy deployment and reduced cost. However,

such a topology are difficult to scale up since

communications between thousands or perhaps

millions of nodes in a ad hoc fashion lead to

degraded performances and hence higher energy

consumption. For instance, routing protocols are a

prominent factor of the scalability of sensor

networks. In recent researches, the proposed routing

protocols require that some of the sensors have

knowledge of the topology of the entire network at

every point in time. This requires a lot of signalling

and do not scale well with a high number of nodes.

Different solutions are proposed in the literature to

overcome these weaknesses. For instance, a

distributed protocol for large-scale WSNs is

proposed in (Tilak, 2003). It is based on localized

interactions and does not require global knowledge

such as the current network topology. In

(Grossglauser, 2001), authors proposed to use

specific mobility patterns in order to achieve higher

capacity in large scale WSNs.

In these studies, the evaluation of the scalability

of the proposed protocols is mainly based on a well

known metric for WSNs which is the network

lifetime. The objective is to avoid significant

degradations of the network lifetime when the

number of nodes composing the WSN increases.

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

Through the analysis of the above sited studies, it

appears that no single architecture can be adopted to

face the scalability issues. Different solutions should

be envisaged since the performances of the WSN

may also depend on the type of applications for

which they have been conceived.

Figure 1: Architecture of a multi-tiered wireless sensor

network.

2.2 Nodes Deployment

It is important to consider the distribution of the

sensors within the phenomena area according to the

needs of the application. We can distinguish three

deployment strategies. The self organization feature

of sensors makes possible to deploy them randomly

over the observed area. In such a case, sensors might

be distributed in a random uniform way, like

dropped from an aircraft. The sensors can also be

regularly deployed in the field as placed on a

predetermined geometric grid. Finally, they can be

placed in a planned manner in order to provide

higher sensor density in a region where the

phenomenon is concentrated.

Random deployment is usually preferred because

more realistic but regular deployment can offer in

some specific cases some advantages. In fact, many

applications require sensors location information to

achieve the desired functionality and since using a

GPS system is not a feasible solution, we choose to

place the sensors over a grid points to have a prior

knowledge of sensors location information. In some

other researches, location estimation techniques are

proposed to get over the problem (Bulusu, 2000),

(Doherty, 2001), (Savvides, 2002), (Nasipuri, 2002).

2.3 Energy Model

Energy consumption in a sensor node has in general

the following components:

a) Sensing energy:

It represents the energy consumed when

activating the sensing circuitry and collecting data

from the environment. The amount of this energy

depends on the task that is assigned to the sensor.

b) Transmission energy:

It represents the energy consumed by the

transmitter and the receiver circuitry of the sensor.

The energy consumption due to transmissions

between node i and node j can be modelled as

jir

jit

rijE

rjiE

.),(

Where:

• E

(i,j) is the energy consumed at node i when

transmitting to node j with a bit rate equal to r

i,j

• E

(j,i) is the energy consumed at node j when

receiving from node i with a bit rate equal to r

i,j

• d

i,j

is the distance between node i and node j.

•

dba +=

•

c) Computation energy

It represents the energy consumed to activate the

sensor’s processing unit in order to operate the

transmitter and receiver circuitry.

Compared to the transmissions energy, the

sensing and computing energies are relatively low.

2.4 Single Hop vs. Multi Hop

When the sensor nodes use single hop

communication, each node sends its data directly to

the sink. In such case, the sensor nodes located

farthest from the sink have to spend the maximum

amount of energy and hence are the first to be dead

whereas in multi-hop communication, the nodes

located closest from the sink are the first to be dead

because they have to relay the farther nodes data.

Moreover, since the communication is directly

between the sensor nodes and the sink, only one

node transmits at the same time and then a

contention less MAC is used.

Multi-hop communication has been vastly

favoured over long-range single-hop links to provide

a large coverage area. The use of multi-hop is

essentially to combat the rapid decay of the received

IMPROVING ENERGY CONSUMPTION IN LARGE SCALE WIRELESS SENSOR NETWORKS WITH MULTIPLE

MOBILE SINKS DEPLOYMENT

signal strength as communication distance increases.

However, multi-hop transmission is not always

better than single-hop transmission in perspective of

energy conservation. In fact, we knew from previous

works that it depends on the distance between the

sensor and the sink node, the number of hop and

each hop distance. A careful investigation ((Chen,

2006), (Bhardwaj, 2001), (Mhatre, 2004)) has

proved that the energy consumption rate is

minimized only when using an optimal hop number

opt

of identical hop distances named characteristic

distance

bad

char

/2=

. We can write

charopt

dDN /=

(D the distance between the

source and the sink node). Consequently, the most

energy efficient scheme is to use single hop if the

distance between the sensor and the sink is no

greater than d

char

, else multi-hop with hop distance

of d

char

2.5 Multiple Mobile Sinks

2.5.1 Why Multiple Sinks?

In recent researches, energy efficient usages of

multiple and/or mobile sinks to increase the network

lifetime were proposed (Gandham, 2003), (Kim,

2005), (Oyman, 2004), (Vincze, 2006). The idea

behind this is to decrease the distance between each

sensor node and the nearest sink. In fact, when a

higher number of sinks are distributed within the

WSN, the path lengths from any sensor node to its

nearest sink is decreased leading to lower energy

consumption and therefore to higher network

lifetime.

However the cost of a sink is more expensive

than the sensor and then the number of sink nodes is

financially constrained. In (Oyman, 2004), the

authors proposed to find the minimum number of

sinks while maximizing the network lifetime by

connecting the budget reserved for the sink nodes

with the lifetime of the sensor nodes.

2.5.2 Why Moving Sink?

In a wireless sensor network where a multi-hop

communication is used, the nodes which are one hop

from the sink drain their energy faster than other

nodes because they have to relay messages

originating from many other nodes in addition to

delivering their own messages. In the case of one-

hop communication, the nodes send directly their

messages to the sink and the nodes farthest from the

sink are the first to drain their energy. In doing so

and in the both cases, many sensor nodes will

become quickly unable to communicate with the

base station and the network becomes inoperational.

Several researches have then demonstrated

analytically and with experimental results that using

multiple mobile sinks increases the network lifetime

(Vincze, 2006), (Luo, 2005).

We note that the sink trajectory can be rather

controlled by the application; it can be mounted on a

remote controlled robot and can be moved from one

point to an other like in (Gandham, 2003). Else, it

can follow a specific mobility model in which case

an estimation of its position can be computed like in

(Chen, 2006).

2.5.3 Existing Approaches

Deploying multiple mobile base stations in WSNs

has been investigated in a dynamically growing

number of papers. We mention hereafter some of the

most relevant.

In (Luo, 2005), the authors have developed an

analytical model that describes the communication

load distribution in WSNs and proved that base

station mobility is a strategy that deserves to be

considered when optimizing the network lifetime.

They have further shown that the optimum

movement strategy for a mobile base station is to

follow the periphery when the deployment area is

circular.

Network lifetime elongation using mobile base

station has also been investigated in (Wang, 2005).

The author gave a novel linear programming

formulation for the joint problem of determining the

movement of the sink and the sojourn time at

different points in the network. The simulations have

shown that lifetime maximizing solutions are

achieved by nonuniform sojourn time distributions

among grid points depending on the shape of the

deployment area.

In (Gandham, 2003), authors propose to divide

time into rounds and to dynamically relocate

multiple sinks, at different positions along the

periphery of the sensed field, at the beginning of

each of these rounds. An integer linear program is

used to determine the new locations of the different

base stations. Results have shown that the energy

consumption of individual sensors is better balanced

and the overall energy consumption of all sensors is

minimized. In (Kim, 2005), authors propose another

approach to find the optimal locations of multiple

stationary sink nodes. The proposed scheme allows

sensor nodes to communicate with one or multiple

sinks through multiple paths in order to improve the

network lifetime. In (Oyman, 2004), authors claim

that finding the optimal placement for a given

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

number of sinks is equivalent to the clustering

problem and should be solved using a clustering

algorithm. Another approach to solve the problem of

multiple mobile base station placements is proposed

in (Vincze, 2006). An electrostatic model is applied

to determine sinks’ locations and to coordinates the

movements of these sinks considering the network

state.

Unfortunately, most of the above strategies are

proposed and evaluated over small to medium size

wireless sensor networks (typically less than 100

nodes). For large scale wireless sensor networks,

where hundreds or thousands of nodes can be

deployed, the placement of multiple sinks still

requires advanced studies. For instance, and as

illustrated on Fig. 2, if we consider the case where

the sinks are located along the periphery as stated in

(Gandham, 2003), the paths between each node and

its nearest sink is relatively short when the number

of nodes is limited. However, the more the area size

increases and/or the number of nodes within it

increases, the longer this path is and the shorter the

sensor nodes lifetime will be.

2.5.4 Sink Velocity Influence

A mobile sink can move in two different regimes

(Luo, 2006), a fast mobility regime and a slow

mobility regime. In the fast mobility regime, the sink

moves in a continuous form with a velocity v along

the time without any stop or pause in a particular

position. In the slow mobility regime, the sink

moves in a discrete form and the sink’s trajectory is

a sequence of anchor points between which the sink

moves with a velocity v and at which it pauses

during a period of time (epoch). The slow mobility

regime is considered more realistic and is adopted in

a big number of researches.

However, it is very important to carefully choose

the value of the sink velocity. In fact, when the

mobile sink velocity is high, the sink will more

frequently change its position and visit more the

different regions over the area in interest during the

network lifetime. Therefore, the energy consumption

is efficiently distributed over the sensors and the

network lifetime extended. This can be much more

efficient in the particular case where the sensors

buffer the data sensed and wait until sink approaches

to deliver it (Chen, 2006) which reduces

unnecessarily packet forwarding actions since

sensors are sure of sink arrival before loosing the

data (because of buffer size limitation or packet

deadline expiration). Besides, the high speed moving

sink produces a tolerable data delivery delay

especially in the case of fast mobility regime, which

can be very important for some specific applications.

However, the mobile sink high velocity can have

negative effects. In fact, it can make the session

interval too short to successfully exchange a long

data packet and hence the packet loss rate will

increase. In slow mobility regime, it is preferred that

the epoch be long enough to guaranty long messages

exchange.

(a) Single sink in a small network

(b) Multiple sinks

in a small network

Figure 2: Multiple sink placement.

2.6 Overhead Problem

Using a moving sink to collect the information in a

static wireless sensor network is a strategy that has

been adopted by several researchers because of its

efficiency in increasing the network lifetime.

However, it seems obvious that the mobility of the

sink will inevitably incur additional overhead in data

exchanges since the nodes will continuously need to

be informed of the sink location. This can be much

more dramatic when the number of sensors is very

large. In (Luo, 2006), the authors evaluated the

performances of MobiRoute, a routing protocol that

supports sink mobility. They proved that when using

a slow mobility regime with an epoch much longer

than the sink moving time, the overhead introduced

by the mobility of the sink became negligible

because amortized across a long epoch. Hence, to

avoid that the overhead offsets the benefits brought

by sink mobility, such a scenario should be adopted.

2.7 Buffering Data

In a static wireless sensor network where the sink is

mobile, the sensors can send the sensed data

IMPROVING ENERGY CONSUMPTION IN LARGE SCALE WIRELESS SENSOR NETWORKS WITH MULTIPLE

MOBILE SINKS DEPLOYMENT

immediately to the sink by direct transmission if the

sink is in the transmission range of the sensor or by

multi-hop communication over the different relay

sensors. In some proposals like (Chen, 2006),

(Chakrabarti, 2003) and (Rahul, 2003), the sensors

hold the data they sense in their buffer until they

encounter the mobile sink. The authors proved that it

represents the most economic way in terms of

energy. However, if the time between two

successive sensor-sink meetings is too long, packets

loss is expected because of the buffer size limitation

or packet deadline expiration as well as an

intolerable delay of data delivery. Hence, an optimal

choice of the value for these parameters is very

important to guaranty the best results in terms of

network lifetime.

2.8 Transmission Range Influence

In wireless sensor networks with moving sinks, the

transmission range is one of the fundamental design

parameter. In fact, depending on if it increases or

decreases, the network topology changes since the

number of one hop neighbours of a sensor as well as

the path length from a sensor to the sink varies

(Youssef, 2002). Besides, when the transmission

range increases, the connectivity of the network

increases and hence the network lifetime is

improved. However, there is a threshold of the

transmission range value over which the

connectivity of the network is no more influenced

whereas the energy consumption becomes dominant

resulting in the network lifetime degradation

(Gandham, 2003). This threshold obviously depends

on the other parameters of the network (number of

sinks, size of the network, transmission energy

model, the initial energy of each sensor…).

Analytical studies in (Chen, 2006) have also shown

that the transmission range can also influence the

data delivery delay, the sensor-sink meeting delay

and the outage or unsuccessful packet transmission

probability. The lager it is, the lower they are.

Through the analysis presented above, it is

obvious that deploying multiple, mobile sinks in

WSNs efficiently reduces the energy consumption

level and further lengthens the network lifetime.

However, as stated before, most of the existing

solutions are appropriate and efficient over small to

medium size wireless sensor networks (typically less

than 100 nodes). Therefore, further investigations

should be conducted in order to optimize multiple

mobile sink placement in large scale wireless sensor

networks, where hundreds or thousands of nodes can

be deployed. Moreover, the fundamental design

parameters discussed previously and which have a

serious influence on the energy consumption should

be carefully chosen in order to let them contribute in

optimizing the network behaviour and extending its

lifetime duration.

3 MULTIPLE SINKS LACEMENT

IN LARGE SCALE WSNS:

PROPOSED APPROACH

We propose in this work to enhance sink placement

in large scale WSNs. An intuitively appropriate

solution is to decompose the underlying sensor

network and then optimize energy usage in each of

the sub-networks independently. The objective is to

take advantage of the powerful and efficient sink

placement techniques proposed for small scale

WSNs. In order to apply these techniques over large

scale WSNs, we propose to first divide the network

into sub-networks according to specific criteria. An

adequate sink placement technique can then be

applied independently within each of the defined

sub-networks.

Graph partitioning is a promising approach to

split a large sensor network into balanced sub-

networks. In practice, different criteria can be

considered in order to partition a large scale wireless

sensor network. One simple objective is to create

balanced sub-networks (in terms of number of

sensors) that group the sensors according to their

neighbourhood. This allows creating smaller sub-

networks with similar characteristics that can be

easily optimized, independently but in the same way.

In graph theory related literature, different

approaches and techniques are proposed for

balanced graph partitioning.

3.1 Existing Graph Partitioning

Techniques

In (Even, 1997), a fast approximate graph

partitioning algorithm is proposed. The authors

unified the problems of b-balanced cuts and k-

multiway separators using a new approach called

minimum capacity ρ-separators. They studied the

graph partitioning problems on graphs with edge

capacities and vertex weights and described a simple

approximation algorithm for minimum capacity ρ-

separators leading to a fast approximation algorithm

both for b-balanced cuts and k-multiway separators.

They define a ρ-separator as a sub-set of edges

whose removal partitions the vertex set into

connected components such that the sum of the

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

vertex weights in each component is at most ρ times

the weight of the graph. In (Ito, 2006), authors

considered three problems to find an (l, u)-partition

of a given graph. They proposed to partition a graph

G into connected components by deleting some

edges from G making the total weight of each

component equal at least to l and at most to u. The

minimum partition problem is to find an (l, u)-

partition with the minimum number of components,

the maximum partition problem is defined in the

same way and the p-partition problem is to find an

(l, u)-partition with a fixed number p of components.

Authors proved that the three problems are NP-

complete or NP-hard. In (Chlebikova, 1996), authors

studied the approximation of the Maximally

Balanced Connected Partition problem (MBCP).

They first presented the optimization problem that

finds the maximally balanced connected partition for

a graph G. It results in a partition (V

, V

) of V

composed of disjoint sets V

and V

such that both

sub-graphs of G induced by V

and V

are

connected, and maximize an objective function

“balance”, B

, V

) = min(w(V

), w(V

)).

Authors proved that the problem is NP-hard.

In this work, this last approach will be adapted

and applied to large scale Wireless Sensor

Networks. Our choice is mainly motivated by the

practical approach provided in (Chlebikova, 1996)

and based on the use of a polynomial-time algorithm

that gives an approximate solution.

In the following the Maximally Balanced

Connected Partition (MBCP) technique (Chlebikova,

1996) is adapted and formulated for partitioning a

large WSN. A corresponding approximate resolution

algorithm is then presented.

3.2 Model Formulation

Assume that G = (V, E) is a connected graph where

V is a set of nodes and E is the set of all links

connecting two nodes of V.

In our case, V represents the set of sensors and E

represents the set of all links connecting two sensors

belonging to V.

The objective is to partition G into connected

balanced sub-graphs (in terms of number of nodes).

We assume that all sensors have the same initial

energy.

To achieve this objective, let w be a non-

negative vertex-weight function representing the

balancing criteria. In this case, w will reflect the

number of nodes. Hence w(V’) = |V’|.

This MBCP problem can then be formulated as

follow:

Maximize B

, V

) = min ( w(V

), w(V

))

Subject to

1. (V

, V

) is a partition of V into

nonempty disjoints sets V

and V

such

that sub-graphs of G induced by V

and

are connected.

(

)

(

)

VVvwVw

⊆∀=

∑

∈

The resolution of this model will result into two

balanced sub-networks. Each of them can be

partitioned again using the same process.

This partitioning technique should be applied as

much as required according to the targeted size for

the sub-networks and taking into account the number

of available sinks to be placed. The final result

should be 2

equivalent smaller sub-networks where

n is the number of partitioning iterations.

3.3 Problem Resolution

To solve this model, we used the polynomial

approximation algorithm presented in (Chlebikova,

1996) that finds an approximate solution for the

MBCP problem.

In order to select neighbouring sensors within the

same sub-networks, we adapted the algorithm by

sorting the list of candidates for each partition

according to their distance (vicinity).

The algorithm can be written as follow:

Input: G = (V, E).

V= {v

, v

… v

} where

|V|.

0. Initialize V

={v

}, V

= V\V

such v

node near the periphery.

1. If | V

| >= 1/2 | V| then Step 3

else Step 2.

2 .Let V

= {u Є V / (V

U {u}, V

\{u})

is a connected partition of G}.

Choose u of V

such that u the closest

element to V

If |u| < |V| - 2|V

then V

:= V

U {u}, V

:= V

\ {u},

Step 1

else Step 3

3. Return (V

, V

4 SIMULATION RESULTS AND

ANALYSIS

The effect of the proposed partitioning technique on

the WSN lifetime is investigated using numerical

simulations over Matlab environment. A circular

large scale wireless sensor network, with a radius R

= 500m is considered. 1000 nodes are randomly

(uniformly) deployed over the network area. Sensors

are similar with a communication range r= 80m and

IMPROVING ENERGY CONSUMPTION IN LARGE SCALE WIRELESS SENSOR NETWORKS WITH MULTIPLE

MOBILE SINKS DEPLOYMENT

an initial energy of 1000J unit. The cost of sending

and receiving operations is 1mJ per packet. Sinks are

assumed to have no energy constraints because they

have larger batteries or their batteries are

rechargeable. Sensors communicate with the sinks in

a multi-hop manner. We assumed that the shortest

path routing algorithm is used to find the shortest

route to the sink. The network lifetime is defined as

the moment at which the first sensor runs out of

energy. Time is divided into rounds. Each round is

composed of T=100 timeframes. Each sensor node

generates one data packet every timeframe.

To evaluate the efficiency of the proposed graph

partitioning technique in elongating the network

lifetime, the following scenario is considered:

Comparative Scenario:

Case 1: The entire network is considered. N sinks

are deployed randomly on the periphery of the

network. Then, the sinks start to move along the

periphery. In one round each sink moved 60 m.

Case 2: The graph partitioning algorithm is used to

define N smaller sub-networks. One single sink is

randomly deployed on the periphery of each sub

network. Then each sink moves 60m each round on

the periphery.

200

400

600

800

1000

1200

248

number of sinks

lifetime duration (rounds)

case1

case2

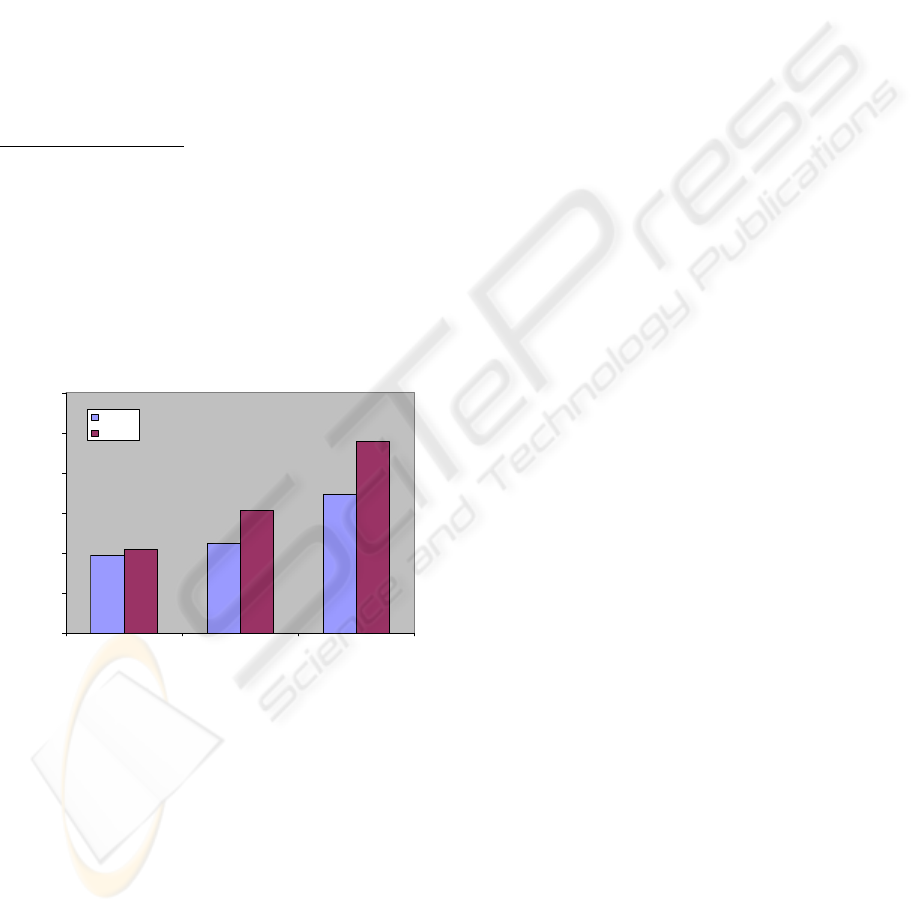
Figure 3: The network lifetime in the comparative

scenario.

Several simulations are then run to compare the

network lifetime in the two different cases of

described scenario.

Simulation results are presented in figure 3. First,

let’s notice that the simple use of multiple sinks

enhances the network lifetime (with and without

partitioning). Indeed, the network lifetime increases

proportionally to the number of sinks because the

distance between the sensors and their correspondent

sinks decreases.

Second, enhancements of the network lifetime

can be observed in the case of partitioned large-scale

WSNs compared to non partitioned ones. This was

expected as when one sink is moving along the

periphery of each sub-network, the energy

consumption is obviously much more distributed

over the sensors than when all the sinks are moving

along the periphery of the whole network. The nodes

that are the closest to the sinks are logically the ones

who die first because they not only send their own

data but also relay the data of all the nodes in the

network. In this scenario, the nodes who die first in

the case of non partitioned network are the nodes

situated all along the periphery whereas in the case

of partitioned network, they are the ones situated

along the peripheries of the different sub-networks.

Then, using the graph partitioning technique to

deploy the sinks distributes the load relay and

decreases the average distance between the sensors

and the sinks. Indeed, the improvement of the

network lifetime of the partitioned network is much

more important when the number of sinks (or sub-

networks) increases.

For interested readers, other comparative

scenarios are investigated and provided with all

details in (Slama, 2008).

5 CONCLUSIONS AND FUTURE

WORK

The use of multiple sinks in large scale wireless

sensor networks is necessary in order to cover large

areas and to minimize energy consumption for data

transmission operations. In this paper, we discussed

the fundamental design parameters considered in

WSNs with multiple sinks and which have a

considerable influence on the energy consumption.

We have shown that they should be carefully chosen

in order to let them contribute in optimizing the

network behaviour and extending its lifetime

duration. We also proposed the use of graph

partitioning techniques to obtain smaller and

balanced sub-networks over which existing sink

placement techniques that are optimized for small to

medium scale WSNs can be used.

Performance results show that the proposed

technique considerably enhances the network

lifetime particularly when the sinks are moving

along the periphery.

This first step using graph partitioning approach

to improve energy consumption in large-scale WSNs

is promising. We will focus in complementary and

future work on more elaborated approaches for

optimal multiple sinks placement and WSN

partitioning. In addition, efficient tools should be

proposed to determine the optimal number of

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

partitions and sinks to be used according to the WSN

characteristics, applications’ requirements and

financial costs.

REFERENCES

Tilak, S., Murphy, A. & Heinzelman, W., 2003. Non-

Uniform Information Dissemination for Sensor

Networks. In ICNP '03, Proceedings of the

International Conference on Network Protocols.

Grossglauser, M. & Tse, D., 2001. Mobility increases the

capacity of ad hoc wireless networks. ACM\IEEE

Transactions on Networking; 10(4):477-486.

Bulusu, N., Heidemann, J. & Estrin, D., 2000. GPS-less

Low Cost Outdoor Localization for Very Small

Devices. IEEE Personal Communications Magazine,

Vol. 7, No. 5, pp. 28-34.

Doherty, L., Pister, K. S. J. & Ghaoui, L. E., 2001.

Convex Position Estimation in Wireless Sensor

Networks. In INFOCOM’01, Proceedings of the 20th

Annual Joint Conference of the IEEE Computer and

Communications Societies pp. 1655-1663, Anchorage,

Alaska, USA.

Savvides, A., Park, H., & Srivastava, M. B., 2002. The

Bits and Flops of the N-hop Multilateration Primitive

for Node Localization Problems. In ACM WSNA’02,

Proceedings of the First ACM International Workshop

on Wireless Sensor Networks and Applications, pp.

112-121, Atlanta, USA.

Nasipuri, A., & Li, K., 2002. A Directionality based

Location Discovery Scheme for Wireless Sensor

Networks. In ACM WSNA’02, Proceedings of the First

ACM International Workshop on Wireless Sensor

Networks and Applications, pp. 105-111, Atlanta,

USA.

Chen, C., Ma, J., & Yu, K., 2006. Designing Energy-

Efficient Wireless Sensor Networks with Mobile

Sinks. In WSW’06 at Sensys’06, Boulder, Colorado,

USA.

Bhardwaj, M., et al., 2001. Upper Bounds on the Lifetime

of Sensor Networks. In ICC’01, Proceedings of the

IEEE international conference on communications,

pp. 785 - 790, Helsinki, Finland.

Mhatre, V. & Rosenberg, C., 2004. Design guidelines for

wireless sensor networks: communication, clustering

and aggregation. In Elsevier Ad Hoc Networks, pp.

45-63, issue 2, 2004.

Gandham, S. R. & al., 2003. Energy Efficient Schemes for

Wireless Sensor Networks With Multiple Mobile Base

Stations. In GLOBECOM’03, Proceeding of the IEEE

Global Communication conference.

Kim, H., Seok, Y., Choi, N., Choi, Y. & Kwon, T., 2005.

Optimal Multi-sink Positioning and Energy-efficient

Routing in Wireless Sensor Networks. In LNCS’05,

Lecture Notes in Computer Science, Vol.3391, pp.264-

274.

Oyman, E. I. & Ersoy, C., 2004. Multiple Sink Network

Design Problem in Large Scale Wireless Sensor

Networks. In ICC’04, Proceeding of the IEE

international conference on communications.

Vincze, K., Fodor, R., Vida, and Vidacs, A., 2006.

Electrostatic Modelling of Multiple Mobile Sinks in

Wireless Sensor Networks. In proceeding of IFIP

Networking Workshop on Performance Control in

Wireless Sensor Networks, pp. 30-37, Coimbra,

Portugal.

Luo, J. & Hubaux, J.-P., 2005. Joint Mobility and Routing

for Lifetime Elongation in Wireless Sensor Networks.

In IEEE Infocom’05, Proceeding of the 28th

Conference on Computer Communications.

Wang, Z. M. & al., 2005. Exploiting Sink Mobility for

Maximizing Sensor Networks Lifetime. In Proceeding

of the 38th Hawaii Intel. Conf. Sys. Sci.

Luo, J., Panchard, J., Piorkowski, M., Grosglausser, M. &

Hubaux, J-P., 2006. Mobiroute: Routing towards a

Mobile Sink for Improving Lifetime in Sensor

Networks. In DCOSS'06, International Conference on

Distributed Computing in Sensor Systems (Systems

track).

Chakrabarti, & al., 2003. Predictable Observer Mobility

for Power Efficient Design of Sensor Networks. In

IPSN’03, Proceedings of ACM/IEEE International

Conference on Information Processing in Sensor

Networks Palo Alto, California, USA.

Rahul, C., Shah, & al., 2003. Data MULEs: Modeling a

Three-tier Architecture for Sparse Sensor Networks. In

Elsevier Ad Hoc Networks, vol. 1, issues 2-3, pp. 215-

233.

Youssef, M.A., Younis, M.F. & Arisha, K.A., 2002. A

Constrained Shortest- Path Energy-Aware Routing

Algorithm for Wireless Sensor Networks. In Wireless

Communication and Networking Conference, 2:794 –

799.

Even, G., Naor, J., Rao, S., & Schieber. B., 1997. Fast

approximate graph partitioning algorithms. In Proc.

8th Ann. ACM-SIAM Symp. on Discrete Algorithms,

ACM-SIAM, pages 639 – 648, 1997.

Ito, T., Zhou, X. & Nishizeki, T., 2006. Partitioning a

graph of bounded tree-width to connected subgraphs

of almost uniform size. Journal of discrete algorithms,

Volume 4, Issue 1, March 2006, Pages 142-154.

Chlebikova, J., 1996. Approximability of the Maximally

balanced connected partition problem in graphs.

Inform. Process. Lett., 60:225 – 230, 1996.

Slama, I., Jouaber, B. & Zeghlache, D., 2008. Energy

Efficient Scheme for Large Scale Wireless Sensor

Networks with Multiple Sinks”, In WCNC’08, Proc.

IEEE Wireless Communications and Networking

conference, Pages 2367-2372.

IMPROVING ENERGY CONSUMPTION IN LARGE SCALE WIRELESS SENSOR NETWORKS WITH MULTIPLE

MOBILE SINKS DEPLOYMENT