A NOVEL FRONT-END NOISE POWER AND SNR ESTIMATION

USING WAVELET-PACKETS IN OFDM SYSTEMS

Rana Shahid Manzoor, Varun Jeoti, Nidal Kamel and Muhammad Asif

Electrical & Electronic Engineering Department, Universiti Teknologi PETRONAS (UTP)

Bandar Seri Iskandar, 31750 Tronoh, Perak Darul Ridzuan, Malaysia

Keywords: SNR, Noise power estimation, Adaptive modulation, OFDM.

Abstract: In this paper, a noise power estimator based on one OFDM preamble is proposed. The estimator, unlike

others, performs noise power estimation at the front-end of the receiver. The proposed estimator takes into

consideration the different noise power levels over the OFDM sub-carriers. The OFDM band is divided into

several sub-bands using wavelet packet and noise in each sub-band is considered white. The second-order

statistics of the transmitted OFDM preamble are calculated in each sub-band and the noise power is

estimated. The proposed estimator is compared with Reddy’s estimator for colored noise in terms of mean

squared error (MSE).

1 INTRODUCTION

Signal-to-noise ratio (SNR) is defined as the ratio of

the desired signal power to the noise power. Noise

variance, and hence SNR estimates of the received

signal, are very important parameters for quality

control in communication systems (Xiaodong et al.,

2005). The search for a good SNR estimation

technique is motivated by the fact that various

algorithms require knowledge of the SNR for

optimal performance. For instance, in OFDM

systems, SNR estimation is used for power control,

adaptive coding and modulation, turbo decoding etc.

SNR estimation indicates the reliability of the

link between the transmitter and receiver. In

adaptive system, SNR estimation is commonly used

for measuring the quality of the channel and

accordingly for changing the system parameters. For

example, if the measured channel quality is low, the

transmitter may add some redundancy or complexity

to the information bits (more powerful coding), or

reduce the modulation level (better Euclidean

distance), or increase the spreading rate (longer

spreading code) for lower data rate transmission.

Therefore, instead of implementing fixed

information rate for all levels of channel quality,

variable rates of information transfer can be used to

maximize system resource utilization with high

quality of user experience (Reddy and Arslan, 2003).

Many SNR estimation algorithms have been

suggested in the last ten years (Kamel and Joeti,

2006), (Bournard, 2003), (Pauluzzi and Norman,

2000) and many have been successfully

implemented in OFDM systems at the back-end of

receiver using the system pilot symbols. The

essential requirement for an SNR estimator in

OFDM system is of low computational load. This is

in order to minimize hardware complexity as well as

the computational time.

In contrast to other SNR estimators, the proposed

technique operates on data collected at the front-end

of the receiver, imposing no restriction on ISI. This

will improve the SNR estimates in severe ISI

channels and also help extending the implementation

of SNR estimators towards systems that require SNR

estimates at the input of the receiver. One such

application is antenna diversity combining, where at

least two antenna signal paths are communicably

connected to a receiver. The combiner can use the

SNR estimates obtained from each antenna signal to

respectively weight them and thereby generate a

combined output signal.

In many SNR estimation techniques, noise is

assumed to be uncorrelated or white. But, in wireless

communication systems, where noise is mainly

caused by a strong interferer, noise is colored in

nature.

In this paper, a front-end noise power and SNR

estimator for the colored noise in OFDM system is

140

Shahid Manzoor R., Jeoti V., Kamel N. and Asif M. (2008).

A NOVEL FRONT-END NOISE POWER AND SNR ESTIMATION USING WAVELET-PACKETS IN OFDM SYSTEMS.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 140-144

DOI: 10.5220/0002023301400144

 SciTePress

proposed. The algorithm is based on the two

identical halves property of time synchronization

preamble used in some OFDM systems. The OFDM

band is divided into several sub-bands using wavelet

packet and noise in each sub-band is considered

white. The second-order statistics of the transmitted

OFDM preamble are calculated in each sub-band

and the power noise is estimated. Therefore, the

proposed approach estimates both local (within

smaller sets of subcarriers) and global (over all sub-

carriers) SNR values. The short term local estimates

calculate the noise power variation across OFDM

sub-carriers. When the noise is white, the proposed

algorithm works as well as the conventional noise

power estimation schemes, showing the generality of

the proposed method.

The remainder of the paper is organized as

follows. In Section 2, the proposed technique is

presented. Section 3 provides the overview of

Reddy’s estimator. Section 4 presents simulation

results and discussion. Section 5 concludes the

paper.

2 FRONT-END BASED

NOISE POWER AND SNR

ESTIMATION TECHNIQUE IN

OFDM SYSTEM

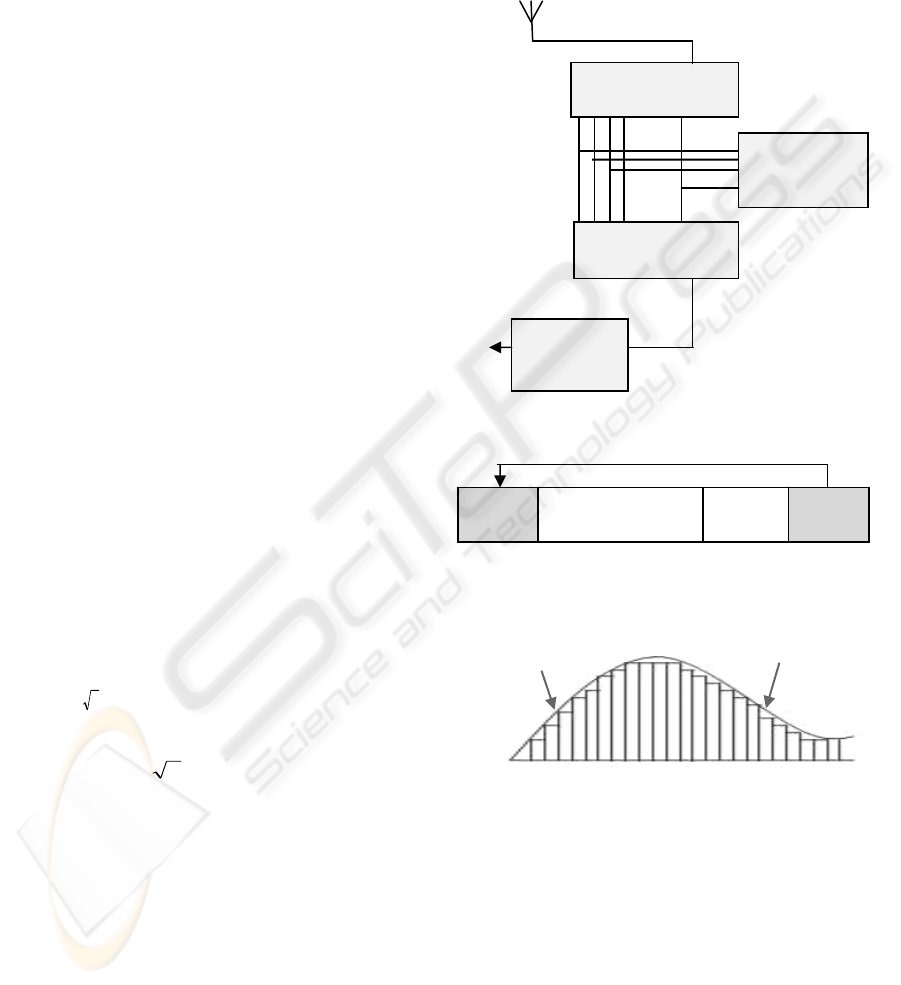
The methodology of the estimator is depicted in the

Fig.1. The synchronization preamble of an OFDM

system - the preamble which has two identical

halves property, is obtained by loading constellation

(QPSK) points with a PN sequence (P

seq

) at even

sub-carriers using eq.1 (IEEE, 2004).

2N21m

12mk 0

2mk m P 2

k P

seq

even

/,....,

)(.

)( =

⎪

⎩

⎪

⎨

⎧

(1)

where the factor of

is related to the 3 dB extra

boost to preamble as compared to data and

''k shows the sub-carriers index. This OFDM

training/synchronization data of length ‘N

OFDM

’ is

sent from the transmitter (T

). Inverse Fourier

transform (IFFT) of transmitted OFDM data is

performed to convert it into time domain. To avoid

intersymbol interference (ISI) cyclic prefix (CP) is

added as shown in Fig 2, so that the total length of

OFDM data becomes L

total

OFDM

+CP.

After adding cyclic prefix, OFDM data is divided

into 2

sub-bands using wavelet packets where ‘n’

shows the number of levels. The length of each sub-

band is L

sub

+ CP

sub

, where Nsub= N

OFDM

and CP

sub =

CP/2

. It inherits the two identical halves

property of synchronization preamble. The noise in

each sub-band is considered white as shown in

Fig.3. The system’s parameters and the structure of

wavelet packet used for the simulations are given in

Table1.

Figure 1: Methodology of proposed technique.

Figure 2: OFDM training symbol with cyclic prefix.

Figure 3: The spectrum of colored noise with approximate

white noise over the sub-bands.

2.1 Signal Power and Noise Power

Estimation

The autocorrelation function of the received signal at

the front-end of receiver in each sub-band, r

(m) has

the following relationship to the autocorrelation of

the transmitted sub-band signal, r

(m) and the noise,

(m):

)()()( mrmrmr

nnssxx

(2)

1 N/2 N

SNR

Estimation

Wavelet Packet

Synthesis

Wavelet Packet

Analysis

OFDM

Demodulator

Colored noise

White noise

A NOVEL FRONT-END NOISE POWER AND SNR ESTIMATION USING WAVELET-PACKETS IN OFDM

SYSTEMS

141

The noise in channel is modeled as additive white

Gaussian noise, thus its autocorrelation function can

be expressed as

)()( mmr

δσ

(3)

where δ(m) is the discreet delta sequence and σ

the

power of noise in the subband.

A study of the OFDM signal shows that, as all the

sub-carriers are present with equal power over the

signal bandwidth, the power spectrum of an OFDM

signal is nearly white and hence its autocorrelation is

also given by

)()( mPmr

sss

(4)

Hence, at zero lag the autocorrelation contains

both the signal power estimate and noise power

estimate indistinguishable from each other.

However, because of the identical halves nature of

the preamble the autocorrelation also has peaks

where cyclic prefix matches with itself and also

where one half matches with other half on both sides

of the zero delay. The autocorrelation of the

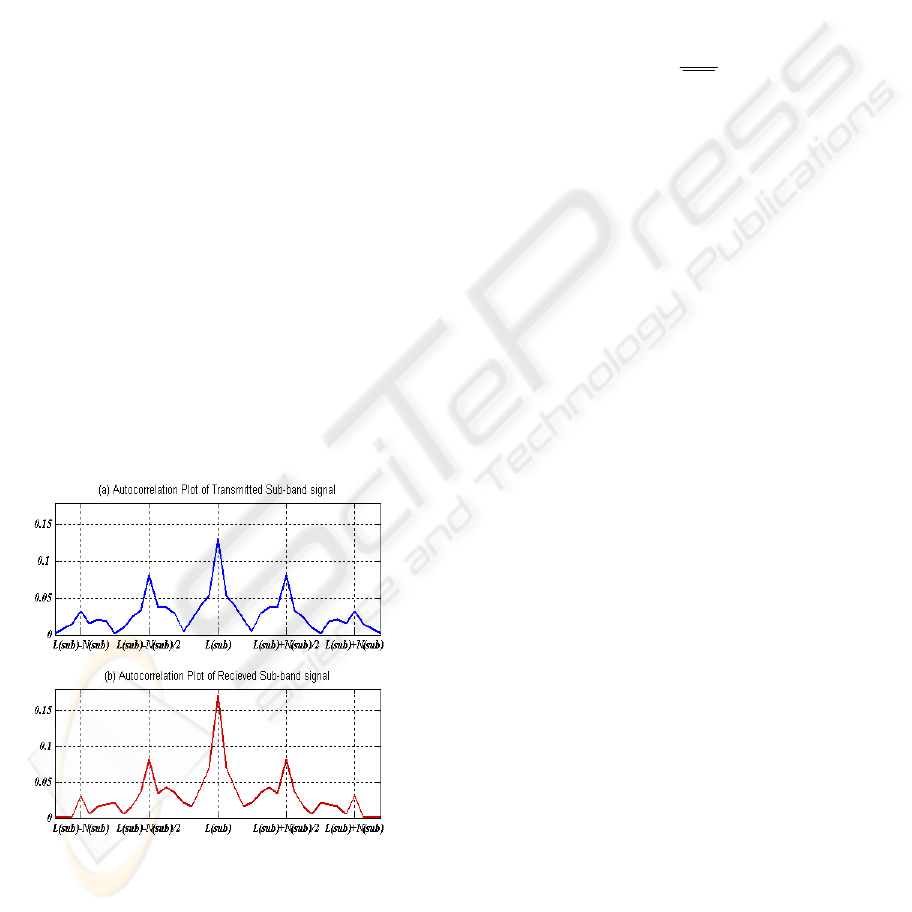
transmitted and received 5

sub-band signal at SNR

= 7 dB are shown in Fig.4(a) and Fig.4(b),

respectively. It is clear that the autocorrelation

values apart from the zero-offset are unaffected by

the AWGN, so one can find the signal and noise

powers from the zero-lag autocorrelation value.

Figure 4: (a) Autocorrelation of transmitted signal. (b)

Autocorrelation of received signal

Taking into consideration the autocorrelation values

for L

sub

-N

sub

/2 and L

sub

-N

sub

lags or L

sub

/2 and

sub

, signal power is given as

(

)

)()/(

subsubxxsubsubxxss

NLr2NLr2P −−−=

(5)

(

)

)()/(

subsubxxsubsubxxss

NLr2NLr2P +−+=

(6)

Having obtained the power of signal in certain sub-

band, noise power can be calculated as

sssubxx

PLr

)(

−=

(7)

Finally we can find the SNR estimates in the sub-

band by using equation (5 or 6) and equation (7).

RNS

(8)

where

∧

SNR

is the estimated value for SNR.

3 REDDY’S SNR ESTIMATOR

FOR COLORED NOISE

In this method channel estimation is performed in

the first realization of the channel, using pilot

symbols and this estimate is used to estimate the

signal noise power. The suggested method can be

used Additive white Gaussian noise (AWGN)

channel and for color dominated channel, in which

the noise power varies across the frequency

spectrum.

The system model is described in the frequency

domain, where a signal is transmitted to obtain the

estimated channel frequency response after which

the instantaneous noise power mean square is

determined. The transmitted signal includes white

noise which is added by the channel of unknown

amplitude. This is modelled in the frequency domain

by the equation:

)()()()( kmkmkmkm

NHXY +=

(9)

where

)(km

= Transmitted signal

)( km

= Received signal

)( km

= Channel white noise

The channel frequency response is estimated by

transmitting preamble and performing division in the

frequency domain of the received signal by the

transmitted signal. When performing the division,

the effect of noise is ignored. The pilot symbols are

then used as the transmitted signal and the received

signal in the pilot sub-carriers is used for the

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

142

received signal and the estimated transfer function

inserted in the equation to determine the noise power

estimate. The noise power estimation is found by

finding the difference between the noisy received

signal and the noiseless signal.

kmkmkm

HXYE

)(

)()()(

ˆˆ

−=

(10)

The difference between the actual channel frequency

response and the estimated is the channel estimation

error.

4 RESULTS AND DISCUSSION

The proposed technique is compared with Reddy’s

estimator for colored noise in OFDM system with

parameters given in Table 1. Wavelet packet 4-level

decomposition is performed with Daubechies-3

wavelet.

SNR is varied from 1 dB to 25 dB for each sub-

band and in order to be statistically accurate, the

mean-squared error (MSE) is derived for the

estimated SNR from 2000 trials according to the

following formula

∑

−=

2000

SNRiRNS

2000

MSE

)

)(

(

(11)

Bias is derived for the estimated SNR using eq.12.

∑

−=

2000

SNRiRNS

2000

Bias ))(

(

(12)

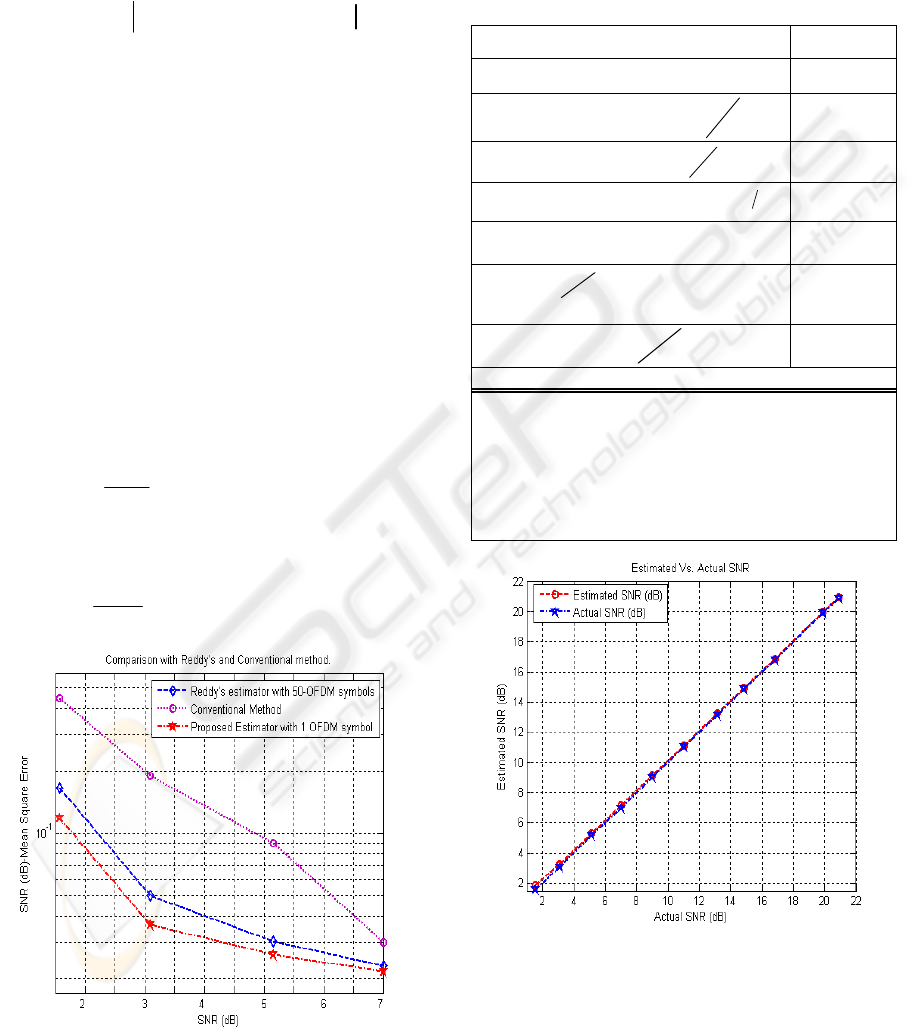
Figure 5: Mean-square-error performance of the proposed

technique.

Fig.5 shows the MSE values for the proposed

algorithm compared with Reddy as a function of

SNR. Fig.6 and Fig.7 shows the actual SNR vs.

estimated SNR comparison and Bias vs. Actual SNR

over all OFDM symbol respectively.

Table1: Parameters for proposed technique.

Figure 6: Actual SNR vs. Estimated SNR of colored noise.

The results show that the proposed estimator gives

better performance in SNR estimation as compared

to Reddy estimator. Thus, for a given SNR, the

proposed technique has lower MSE at all SNRs. It is

also observed that, by using wavelet packet analysis

Ifft size

256

Sampling Frequency =

.20MHz

Sub Carrier Spacing=

Ifft

=Δ

101×

Useful Symbol Time =

101

−

CP Time =

where

41=G

105.2

−

OFDM Symbol Time =

TTT

gbs

1025.1

−

(Because ¼ CP

makes the sampling faster by 5/4 times)

1056.1

−

sub

108.9

−

Wavelet Packet Object Structure

Wavelet Decomposition Command : wpdec

Size of initial data : [1 320]

Order= 2 and Deptth=: 4

Terminal nodes : [15 16 17 18 19 20 21 22 23 24

25 26 27 28 29 30]

--------------------------------------------------

Wavelet Name : Daubechies (db3) ,

Entropy Name : Shannon

A NOVEL FRONT-END NOISE POWER AND SNR ESTIMATION USING WAVELET-PACKETS IN OFDM

SYSTEMS

143

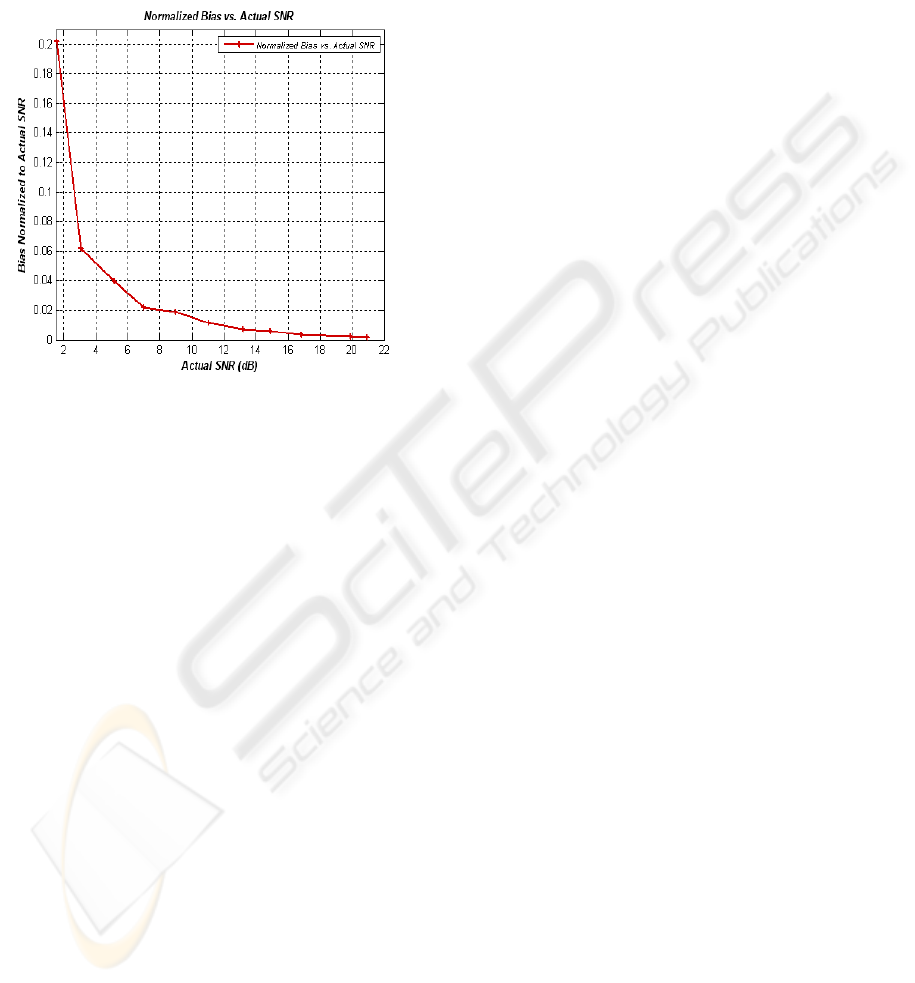
technique, the proposed technique can estimate local

statistics of the noise power when the noise is

colored. The proposed estimator fulfills the criteria

of a good SNR estimator because it is unbiased (or

exhibits the smallest Bias) and has the smallest

variance of SNR estimates as shown from results

clearly.

Figure 7: Olot of Normalized Bias vs. Actual SNR.

The proposed front-end estimator has relatively low

computational complexity (~2N

) because it makes

use of only one OFDM preamble signal and relies on

the autocorrelation of the same to find the SNR

estimates. Reddy’s estimator has relatively more

computational complexity (~50N

) as compared to

proposed estimator as its works after FFT and makes

use of 50 OFDM symbols to find the SNR estimates.

5 CONCLUSIONS

In this paper, a novel front-end noise power and

SNR estimation technique using wavelet-packets is

presented. Also, variation of the noise power across

OFDM sub-carriers is allowed. Therefore, the

proposed approach estimates both local (within

smaller sets of subcarriers) and global (over all sub-

carriers) SNR values. The short term local estimates

calculate the noise power variation across OFDM

sub - carriers. These estimates are specifically very

useful for diversity combining, adaptive modulation,

and optimal soft value calculation for improving

channel decoder performance. Its performance has

been evaluated via computer simulations using

AWGN and multipath fading channels and

implemented in OFDM systems. The results show

that the current estimator performs better than other

conventional methods. Complexity to find SNR

estimates is lower because the current estimator

makes use of only one OFDM preamble signal. The

current estimator fulfills the criteria of good SNR

estimator as it is unbiased and has the smallest

variance of SNR estimates.

REFERENCES

Xiaodong X., Ya Jing. and Xiaohu Y.,2005 “Subspace-

Based Noise Variance and SNR Estimation for OFDM

Systems”, IEEE Wireless Communications and

Networking Conference.

Reddy, S. and Arslan H., 2003 “Noise Power and SNR

Estimation for OFDM Based Wireless Communication

Systems”, Wireless Communication and Signal

Processing Group.

Kamel N.S. and Joeti V., 2006 “Linear prediction based

approach to SNR estimation in AWGN channel”, 23

Biennial Sympiosium on Communications.

Bournard, S., 2003 “Novel Noise Variance and SNR

Estimation Algorithm for Wireless MIMO OFDM

Systems”, IEEE GLOBECOM.

Pauluzzi D.R. and Norman C.B., 2000 “A Comparison of

SNR Estimation techniques for the AWGN Channel”,

IEEE Transactions on Communications, Vol. 48.

IEEE 802.16-2004., 2004”IEEE Standard for Local and

Metropolitan Area Networks Part 16: Air Interface for

Fixed Broadband Wireless Access Systems”.

Prasad, R., 2004, OFDM for Wireless Communications

Systems, Boston, Artech House Inc.

H. Van Trees, 1968 “Detection, Estimation, and

Modulation Theory”, vol.1, New York, Wiley.

H. Hayes, 1996, Statistical Digital Signal Processing and

Modeling, JohnWiley,

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

144