
IMPROVEMENT OF THE SIMPLIFIED FTF-TYPE ALGORITHM
Madjid Arezki, Ahmed Benallal, Abderezak Guessoum
LATSI Laboratory - Department of Electronics, Faculty of Engineering-University of Blida, Algeria
Daoud Berkani
Signal & Communications Laboratory - (ENP), Algiers, Algeria
Keywords: Fast RLS, NLMS, FNTF, Adaptive Filtering, Convergence Speed, Tracking capability.
Abstract: In this paper, we propose a new algorithm M-SMFTF which reduces the complexity of the simplified FTF-
type (SMFTF) algorithm by using a new recursive method to compute the likelihood variable. The
computational complexity was reduced from 7L to 6L, where L is the finite impulse response filter length.
Furthermore, this computational complexity can be significantly reduced to (2L+4P) when used with a
reduced P-size forward predictor. Finally, some simulation results are presented and our algorithm shows an
improvement in convergence over the normalized least mean square (NLMS).
1 INTRODUCTION
In general the problem of system identification
involves constructing an estimate of an unknown
system given only two signals, the input signal and a
reference signal. Typically the unknown system is
modelled linearly with a finite impulse response
(FIR), and adaptive filtering algorithms are
employed to iteratively converge upon an estimate
of the response. If the system is time-varying, then
the problem expands to include tracking the
unknown system as it changes over time (Haykin,
2002) and (Sayed, 2003). There are two major
classes of adaptive algorithms. One is the least mean
square (LMS) algorithm, which is based on a
stochastic gradient method (Macchi, 1995). Its
computational complexity is of O(L), L is the FIR
filter length. The other class of adaptive algorithm is
the recursive least-squares (RLS) algorithm which
minimizes a deterministic sum of squared errors
(Treichler, 2001). The RLS algorithm solves this
problem, but at the expense of increased
computational complexity of O(L
2
). A large number
of fast RLS (FRLS) algorithms have been developed
over the years, but, unfortunately, it seems that the
better a FRLS algorithm is in terms of computational
efficiency, the more severe is its problems related to
numerical stability (Treichler, 2001). The fast
transversal filter (FTF) (Cioffi, 1984) algorithm is
derived from the RLS by the introduction of forward
and backward predictors. Its computational
complexity is of O(L). Several numerical solutions
of stabilization, with stationary signals, are proposed
in the literature (Benallal, 1988), (Slock, 1991) and
(Arezki, 2007). Another way of reducing the
complexity of the fast RLS algorithm has been
proposed in (
Moustakides, 1999) and (Mavridis,
1996). When the input signal can be accurately
modelled by a predictor of order P, the fast Newton
transversal filter (FNTF) avoids running forward and
backward predictors of order L, which would be
required by a FRLS algorithm. The required
quantities are extrapolated from the predictors of
order P (P << L). Thus, the complexity of the FNTF
falls down to (2L+12P) multiplications instead of
8L. Recently, the simplified FTF-type (SMFTF)
algorithm (Benallal, 2007) developed for use in
acoustic echo cancellers. This algorithm derived
from the FTF algorithm where the adaptation gain is
obtained only from the forward prediction variables.
The computational complexity of the SMFTF
algorithm is 7L. In this paper, we propose more
complexity reduction of the simplified FTF-type
algorithm by using a new recursive method to
compute the likelihood variable. The computational
complexity of the proposed algorithm is 6L and this
computational complexity can be significantly
reduced to (2L+4P) when used with a reduced P-size
forward predictor. At the end, we present some
simulation results of the M-SMFTF algorithm.
156
Arezki M., Benallal A., Guessoum A. and Berkani D. (2008).
IMPROVEMENT OF THE SIMPLIFIED FTF-TYPE ALGORITHM.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 156-161
DOI: 10.5220/0001940001560161
Copyright
c
SciTePress
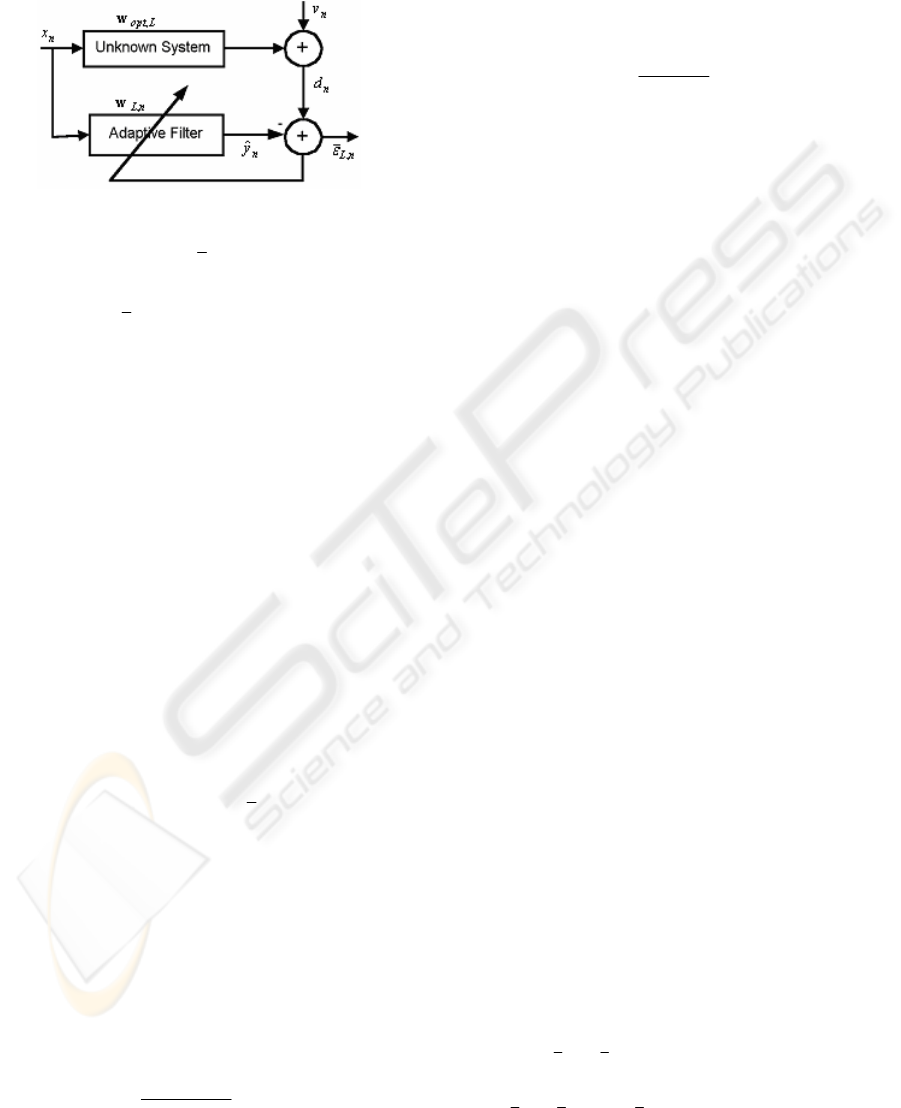
2 ADAPTIVE ALGORITHMS
The main identification block diagram of a linear
system with finite impulse response (FIR) is
represented in
Figure 1.
Figure 1: Main block diagram of an adaptive filter.
The output a priori error
nL,
ε
of this system at time
n is:
nnnL
yd
ˆ
,
−
=
ε
(1)
where
nLnLn
y
,
T
1,
ˆ
xw
−
= is the model filter output,
[]
T
121,
...,,,
+−−−
=
LnnnnL
xxxx is a vector containing
the last L samples of the input signal
n
x ,
[]
T
1,1,21,11,
...,,,
−−−−
=
nLnnnL
wwww is the coefficient
vector of the adaptive filter and L is the filter length.
The desired signal from the model is:
nLLoptnn
vd
,
T
,
xw+=
(2)
where
[]
T
,2,1,
,
...,,,
Loptoptopt
Lopt
www=w represents
the unknown system impulse response vector and
n
v is a stationary, zero-mean, and independent noise
sequence that is uncorrelated with any other signal.
The superscript (.)
T
describes transposition. The
filter is updated at each instant by feedback of the
estimation error proportional to the adaptation gain,
denoted as
nL,
g
, and according to
nLnLnLnL ,,1,,
ε
gww
+
=
−
(3)
The different algorithms are distinguished by the
gain calculation.
2.1 The NLMS Algorithm
The Algorithms derived from the gradient (Macchi,
1995), for which the optimization criterion
corresponds to a minimization of the mean-square
error. For the normalized LMS (NLMS) algorithm,
the adaptation gain is given by:
nL
nx
nL
cL
,
0,
,
xg
+
=
π
μ
(4)
where
μ
is referred to as the adaptation step and
0
c
is a small positive constant used to avoid division by
zero in absence of the input signal. The stability
condition of this algorithm is 0<
μ
<2 and the fastest
convergence is obtained for
μ
= 1 (Slock, 1993).
The power of input signal
nx,
π
is given by:
L
nL
nL
nx
,
T
,
,
xx
=
π
(5a)
It can alternatively be estimated using following
recursive equation (Gilloire, 1996):
2
1,,
)1(
nnxnx
x
γπγπ
+−=
−
(5b)
where
γ
is a forgetting factor ( L/1≈
γ
). The
computational complexity of the NLMS algorithm is
2
L multiplications per sample for the version with
the recursive estimator (5b).
2.2 The SFRLS Algorithm
The filter
nL,
w is calculated by minimizing the
weighted least squares criterion according to
(Haykin, 2002):
(
)
∑
=
−
−=
n
i
iL
T
nLi
in
n
dJ
1
2
,,
)( xww
λ
(6)
where
λ denotes the exponential forgetting factor
(0
<λ≤1). The adaptation gain is given by:
FRLS
,,
RLS
,
1
,,
~
nLnLnLnLnL
kxRg
γ
==
−
(7)
where
nL,
R is an estimate of the correlation matrix
of the input signal vector. The variables
nL,
γ
and
nL,
~
k respectively indicate the likelihood variable
and normalized Kalman gain vector. The calculation
complexity of a FRLS algorithm is 7
L. This
reduction of complexity has made all FRLS
algorithms numerically unstable. The numerical
stability is obtained by using some redundant
formulae of the FRLS algorithms (Benallal, 1988),
(Slock, 1991) and (Arezki, 2007). The numerical
stability is obtained by using a control variable,
called also a divergence indicator
n
ξ
(Arezki,
2007), theoretically equals to zero. Its introduction
in an unspecified point of the algorithm modifies its
numerical properties. This variable is given by:
⎩
⎨
⎧
≠
=
−=
practical0
theory0
f
,
,
nL
nL
n
rr
ξ
(8)
where
nL
r
,
,
0
f
,nL
r and
1
f
,nL
r are the backward a priori
prediction errors calculated differently in tree ways.
IMPROVEMENT OF THE SIMPLIFIED FTF-TYPE ALGORITHM
157

We define three backward a priori prediction errors
(
γ
nL
r
,
,
β
nL
r
,
,
b
,nL
r ), theoretically equivalents, which
will be used to calculate the likelihood variable
nL,
γ
,
the backward prediction error variance
nL,
β
and the
backward prediction
nL,
b
. We introduce these
variables into the algorithm, and we use suitably the
scalar parameters
),,(
b
μμμ
βγ
and
s
μ
, in order to
obtain the numerical stability. For appropriate
choices, we selected the following control
parameters:
1,0 ===
b
μμμ
βγ
;
s
μ
=0.5
(9)
It can be shown that the variance of the numerical
errors in the backward predictor, with the
assumption of a white Gaussian input signal, is
stable under the following condition (Arezki, 2007):
5.32
1
1
74
54
+
−=
+
+
>
LL
L
λ
(10)
These conditions can be written in another simpler
form
pL/11−=
λ
, where the parameter p is a real
number strictly greater than 2 to ensure numerical
stability. The resulting stabilized FRLS (SFRLS)
algorithms have a complexity of 8L; it is given in
Table 1. Note that numerical stabilization of the
algorithm limits the range of the forgetting factor
λ
(condition (10)) and consequently their
convergence speed and tracking ability.
Table 1: SFRLS (8L) algorithm.
Initialization:
100/
2
0
LE
x
σ
≥ ;
00,00,0,
;;1 EE
L
L
LL
===
βλαγ
;
LLLLL
0
~
0,0,0,0,
==== kbaw
Variables available at the discrete-time index n:
1,1,1,1,1,1,1,
;;;;
~
;;
−−−−−−− nLnLnLnLnLnLnL
wkba
βαγ
New information:
n
x ,
n
d
Modeling of
n
x ,
Ln
x
−
1,
T
1,, −−
−=
nLnLnnL
xe xa
;
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
−
−
−
+
+
+
+
+
1,
1,
,
1,
,1
,
,1
1
~
0
~
~
~
nL
nL
nL
nL
nL
nL
nL
e
k
ak
k
k
λα
;
1,1,,1,,
~
−−−
+=
nLnLnLnLnL
e kaa
γ
;
2
,1,1,,
nLnLnLnL
e
−−
+=
γλαα
;
nLnLLnnL
xr
,
T
1,,
xb
−−
−=
;
+
+−
=
nLnLnL
kr
,11,
0
f
,
~
λβ
;
+
+−−
+−
=
nLnLnL
L
nL
kr
,11,1,
1
1
f
,
~
αγλ
])1[(
1
f
,
0
f
,, nLsnLsnLn
rrr
μμξ
+−−=
;
nnLnL
rr
ξμ
γγ
+=
,,
;
nnLnL
rr
ξμ
ββ
+=
,,
;
n
b
nL
b
nL
rr
ξμ
+=
,,
;
1,,1,,
~
~
~
−
+
+
+
+=
nLnLnLnL
k bkk
;
1,
2
,,
1,
,
)(
−
−
−
=
nL
nL
L
nL
nL
nL
r
γ
λα
λα
γ
γ
;
nLnL
b
nLnLnL
r
,,,1,,
~
kbb
γ
+=
−
;
2
,,1,,
)(
β
γλββ
nLnLnLnL
r+=
−
;
nLnLnnL
d
,
T
1,,
xw
−
−=
ε
;
nLnLnLnLnL ,,,1,,
~
kww
γε
+=
−
2.3 The SMFTF Algorithm
The Simplified FTF-type (SMFTF) algorithm
(Benallal, 2007) derived from the FTF algorithm
where the adaptation gain is obtained only from the
forward prediction variables. The backward
prediction variables, which are the main source of
the numerical instability in the FRLS algorithms
(Benallal, 1988), (Slock, 1991) and (Arezki, 2007),
are completely discarded. By using only forward
prediction variables and adding a small
regularization constant
a
c and a leakage factor
η
,
we obtain a robust numerically stable adaptive
algorithm that shows the same performances as
FRLS algorithms.
Discarding the backward predictor does not
mean that the last components
nL,
w
are not updated,
but they are updated by components coming from
lower positions of
nL,
~
k . To avoid the instability of
the algorithm, we append a small positive constant
a
c to the denominator )/(
1,, anLnL
ce +
−
λα
, and it
might be preferable to have the forward predictor
nL,
a
return back to zero by doing
nL,
a
η
, where
η
is a close to one constant (Slock, 1993). The
computational complexity of the SMFTF algorithm
is 7L; it is given in Table 2.
Table 2: SMFTF (7L) algorithm.
Initialization:
LLLL
0
~
0,0,0,
=== kaw ; ;;1
00,0,
E
L
LL
λαγ
== 100/
2
0
LE
x
σ
≥
Variables available at the discrete-time index n:
1,1,1,1,1,
;;;
~
;
−−−−− nLnLnLnLnL
wka
αγ
New information:
n
x ,
n
d
1,
T
1,, −−
−=
nLnLnnL
xe xa
;
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
− 1,
1,
,
1,
,
1
~
0
*
~
nL
anL
nL
nL
nL
c
e
ak
k
λα
;
{
}
1,1,,1,,
~
−−−
+=
nLnLnLnLnL
e kaa
γη
;
2
,1,1,, nLnLnLnL
e
−−
+=
γλαα
nLnL
nL
,
T
,
,
~
1
1
xk+
=
γ
;
nLnLnnL
d
,
T
1,,
xw
−
−=
ε
;
nLnLnLnLnL ,,,1,,
~
kww
γε
+=
−
3 PROPOSED ALGORITHMS
3.1 The M-SMFTF Algorithm
We propose more complexity reduction of the
simplified FTF-type (M-SMFTF) algorithm by using
a new recursive method to compute the likelihood
variable. Let us replace the quantity (*), that has not
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
158

been used in
nL,
~
k of the MSFTF algorithm (Table
2), by the variable
nL
c
,
, we obtain:
⎥
⎦
⎤
⎢
⎣
⎡
−
+
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
− 1,
1,
,
1,
,
,
1
~
0
~
nL
anL
nL
nL
nL
nL
c
e
c
ak
k
λα
(11)
By exploiting certain invariance properties by
shifting the vector input signal extended to the order
(L +1), we obtain two writing manners of input
vector:
[]
T
T
,
,1
,
LnnL
nL
x
−
+
= xx
(12a)
[]
T
T
1,
,1
,
−
+
=
nLn
nL
x xx
(12b)
By multiplying on the left, the members of left and
right of the expression (11) by equations (12a) and
(12b) respectively, the following equality is
obtained:
=+
−LnnLnLnL
xc
,,
T
,
~
kx
anL
nL
nLnL
c
e
+
+
−
−−
1,
2
,
1,
T
1,
~
λα
kx
(13)
By manipulating the relation (13), we obtain a new
recursive formula for calculating the likelihood
variable as given below:
1,,
1,
,
1
−
−
+
=
nLnL
nL
nL
γδ
γ
γ
(14)
LnnL
anL
nL
nL
xc
c
e
−
−
−
+
=
,
1,
2
,
,
λα
δ
(15)
After a propagation analysis of the numerical
errors of the 1
st
order and an asymptotic study of the
equations of errors propagation, we approximate the
errors in the forward variables (
nL,
aΔ ,
nL,
α
Δ ) and
the Kalman variables (
1,
~
−
Δ
nL
k ,
1, −
Δ
nL
γ
) by the
linear first order models deduced from
differentiating (
nL,
a
,
nL,
α
) and (
nL,
~
k ,
nL,
γ
)
respectively. We can thus say that the system is
numerically stable, in the mean sense, for
λ
and
η
between zero and one. It can be shown that the
variance of the numerical errors in the forward
predictor, with the assumption of a white Gaussian
input signal, is stable under the following condition:
)2(
)2(1
1
11
1
2
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−++
−>
L
L
η
λ
(16)
We notice that the lower bound of this condition
is always smaller than the lower bound of condition
(10) of the original numerically stable FRLS
algorithm, which means that we can choose smaller
values for the forgetting factor for the proposed
algorithm and consequently have faster convergence
rate and better tracking ability. The computational
complexity of the M-SMFTF algorithm is 6L; it is
given in Table 3.
Table 3: M-SMFTF (6L) algorithm.
Initialization:
LLLL
0
~
0,0,0,
=== kaw ; ;;1
00,0,
E
L
LL
λαγ
== ; 100/
2
0
LE
x
σ
≥
Variables available at the discrete-time index n:
1,1,1,1,1,
;;;
~
;
−−−−− nLnLnLnLnL
wka
αγ
New information:
n
x ,
n
d .
1,
T
1,, −−
−=
nLnLnnL
xe xa
;
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
− 1,
1,
,
1,
,
,
1
~
0
~
nL
anL
nL
nL
nL
nL
c
e
c
ak
k
λα
;
{
}
1,1,,1,,
~
−−−
+=
nLnLnLnLnL
e kaa
γη
;
2
,1,1,, nLnLnLnL
e
−−
+=
γλαα
LnnL
anL
nL
nL
xc
c
e
−
−
−
+
=
,
1,
2
,
,
λα
δ
;
1,,
1,
,
1
−
−
+
=
nLnL
nL
nL
γδ
γ
γ
nLnLnnL
d
,
T
1,,
xw
−
−=
ε
;
nLnLnLnLnL ,,,1,,
~
kww
γε
+=
−
3.2 The Reduced M-SMFTF Algorithm
The Reduced size predictors in the FTF algorithms
have been successfully used in the FNTF algorithms
(
Moustakides, 1999), (Mavridis, 1996) and (Benallal,
2007). The proposed algorithm can be easily used
with reduced size prediction part. If we denote P the
order of the predictor and L the size of adaptive
filter, the normalized Kalman gain is given by:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
−
PL
nP
anP
nP
nL
nL
nL
c
e
c
0
1
~
0
~
1,
1,
,
1,
,
,
a
k
k
λα
(17)
where P is much smaller than L. The first (P+1)
components of the
nL,
~
k are updated using the
reduced size forward variables, the last components
are just a shifted version of the (P+1)
th
component of
nL,
~
k . For this algorithm, we need two likelihood
variables: the first one
nP,
γ
, is used to update the
forward prediction error variance
nP,
α
, where
nP
c
,
is (P+1)
th
component of
nL,
~
k . The second likelihood
variable
nL,
γ
, is used to update the forward predictor
nP,
a of order P and the transversal filter
nL,
w
.
The computational complexity of this algorithm
is (2L+4P); it is given in Table 4.
IMPROVEMENT OF THE SIMPLIFIED FTF-TYPE ALGORITHM
159
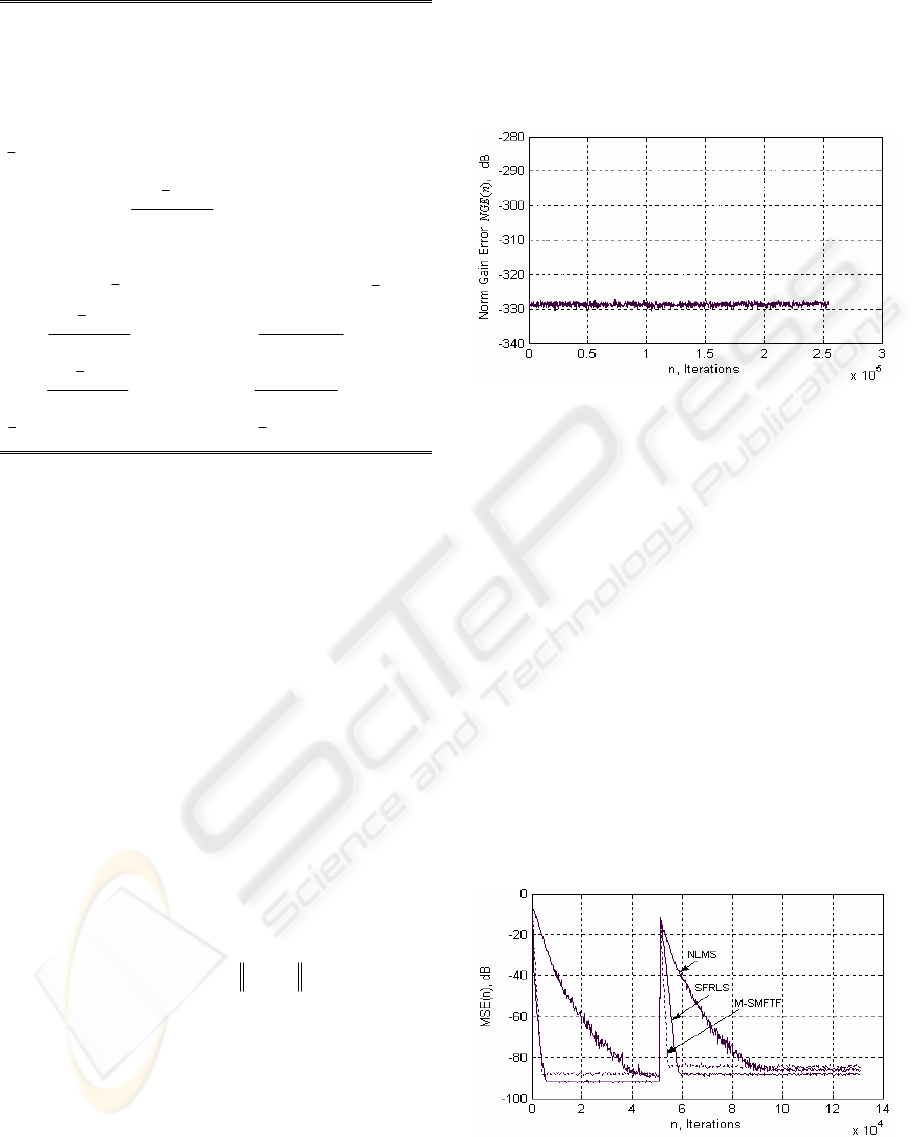
Table 4: Reduced M-SMFTF (2L+4P) algorithm.
Initialization:
100/
2
0
PE
x
σ
≥ ;
00,0,
;1 E
P
PP
λαγ
== ;
1
0,
=
L
γ
;
LLL
0
~
0,0,
== kw ;
PP
0
0,
=a
.
Variables available at the discrete-time index n:
1,1,1,1,1,
;;;
~
;
−−−−− nLnLnLnLnL
wka
αγ
;
New information:
n
x
,
n
d
.
1,
T
1,, −−
−=
nPnPnnP
xe xa
;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
−
PL
nP
anP
nP
nL
nL
nL
c
e
c
0
1
~
0
~
1,
1,
,
1,
,
,
a
k
k
λα
;
):1(
~
~
1,1,
P
nLnP −−
= kk
;
)1(
~
,,
+= Pc
nLnP
k
;
{
}
1,1,,1,,
~
−−−
+=
nPnLnPnPnP
e kaa
γη
;
2
,1,1,, nPnPnPnP
e
−−
+=
γλαα
PnnP
anP
nP
nP
xc
c
e
−
−
−
+
=
,
1,
2
,
,
λα
δ
;
1,,
1,
,
1
−
−
+
=
nPnP
nP
nP
γδ
γ
γ
;
LnnL
anP
nP
nL
xc
c
e
−
−
−
+
=
,
1,
2
,
,
λα
δ
;
1,,
1,
,
1
−
−
+
=
nLnL
nL
nL
γδ
γ
γ
;
nLnLnnL
d
,
T
1,,
xw
−
−=
ε
;
nLnLnLnLnL ,,,1,,
~
kww
γε
+=
−
4 SIMULATION RESULTS
To confirm the validity of our analysis and
demonstrate the improved numerical performance,
some simulations are carried out. For the purpose of
smoothing the curves, error samples are averaged
over 256 points. The forgetting factor
λ
and the
leakage factor
η
for the M-SMFTF algorithm are
chosen according to (16) with the stationary input. In
our experiments, we have used values of
a
c
comparable with the input signal power.
4.1 The M-SMFTF Case
We define the norm gain-error by )(nNGE . This
variable is used in our simulations to check the
equality of the expressions of the likelihood
variables. It is calculated by:
{
}
⎟
⎠
⎞
⎜
⎝
⎛
Δ=
2
,10
Elog10)(
nL
nNGE g
(18)
where
(
)
nL
f
nL
nL
d
nLnL ,
,
,,,
~
~
kkg
γγ
−=Δ is gain-error
vector,
d
nL,
γ
and
f
nL,
γ
are likelihood variables
calculated by SMFTF and M-SMFTF algorithms
respectively. We have simulated the algorithms to
verify their correctness. The input signal
n
x used in
our simulation is a white Gaussian noise, with mean
zero and variance one. The filter length is L=32, we
run the SMFTF and M-SMFTF algorithms with a
forgetting factor (
)/11( L
−
≥
λ
)
λ
=0.9688, the
leakage factor
η
=0.98 and
a
c =0.1. In Figure 2, we
give the evolution in decibels of the norm gain-
error
)(nNGE , we can see that the round-off error
signal stays constant. The M-SMFTF and the
SMFTF algorithms produce exactly the same
filtering error signal.
Figure 2: Evolution of the norm gain-error )(nNGE ;
L=32,
λ
=0.9688,
η
=0.98,
a
c =0.1, E
0
=0.5.
We used a stationary correlated noise with a
spectrum equivalent to the average spectrum of
speech, called USASI noise in the field of acoustic
echo cancellation. This signal, with mean zero and
variance equal to 0.32, sampled at 16 kHz is filtered
by impulse response which represents a real impulse
response measured in a car and truncated to 256
samples. We compare the convergence speed and
tracking capacity of the M-SMFTF algorithm with
SFRLS and NLMS algorithms. The NLMS (
μ
=1)
and SFRLS (
L3/11
−
=
λ
) algorithms are tuned to
obtain fastest convergence. We simulated an abrupt
change in the impulse response by multiplying the
desired signal by 1.5 in the steady state at the
51200
th
samples. Figure 3 shows that better
performances in convergence speed are obtained for
the M-SMFTF algorithm.
Figure 3: Comparative performance of the M-SMFTF,
SFRLS and NLMS for USASI noise, L=256, M-SMFTF:
λ
=0.9961,
η
=0.985,
a
c =0.5, E
0
=1; SFRLS:
λ
=0.9987;
NLMS:
μ
=1.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
160
The differences in the final
)(nMSE for the M-
SMFTF and SFRLS algorithms are due to the use of
different forgetting factors
λ
.
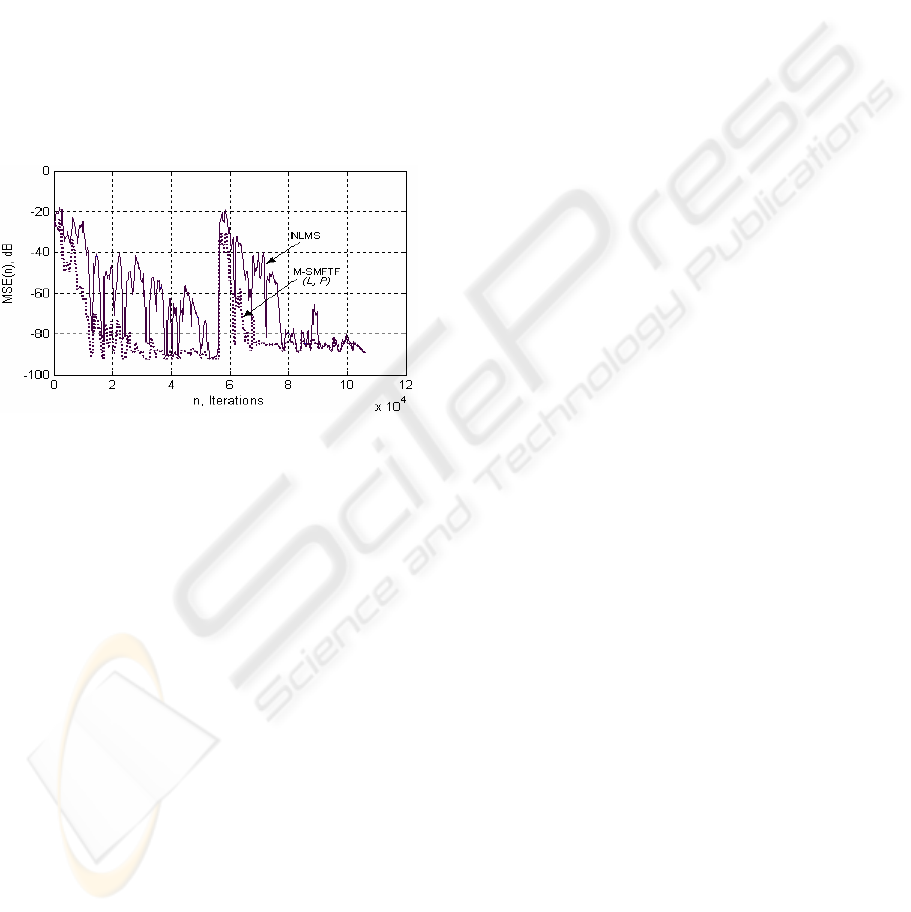
4.2 The Reduced M-SMFTF Case
In this simulation, we compare the convergence
performance of reduced size predictor M-SMFTF
algorithm and the NLMS algorithm. Figure 4
presents the results obtained with the speech signal,
sampled at 16 kHz, for the filter order L=256. We
simulated an abrupt change in the impulse response
at the 56320
th
samples. We use the following
parameters: the predictor order is P=20, the
forgetting factor is
P/11
−
=
λ
. From this plot, we
observe that the re-convergence of M-SMFTF is
again faster than NLMS.
Figure 4: Comparative performance of the M-SMFTF and
NLMS with speech input, L=256, M-SMFTF: P=20,
λ
=0.950,
η
=0.99,
a
c =0.1, E
0
=1; NLMS:
μ
=1.
Different simulations have been done for
different sizes L and P, and all these results show
that there is no degradation in the final steady-
state
)(nMSE of the reduced size predictor algorithm
even for P<<L. The convergence speed and tracking
capability of the reduced size predictor algorithm
can be adjusted by changing the choice of the
parameters
λ
,
η
and
a
c .
5 CONCLUSIONS
We have proposed more complexity reduction of
SMFTF (M-SMFTF) algorithm by using a new
recursive method to compute the likelihood variable.
The computational complexity of the M-SMFTF
algorithm is 6L operations per sample and this
computational complexity can be significantly
reduced to (2L+4P) when used with a reduced P-size
forward predictor (P<<L). The low computational
complexity of the M-SMFTF when dealing with
long filters and it a performance capabilities render
it very interesting for applications such as acoustic
echo cancellation. The simulation has shown that the
performances of M-SMFTF algorithm are better
than those of NLMS algorithm. The M-SMFTF
algorithm outperforms the classical adaptive
algorithms because of its convergence speed which
approaches that of the RLS algorithm and its
computational complexity which is slightly greater
than the one of the NLMS algorithm.
REFERENCES
Arezki, M., Benallal, A., Meyrueis, P., Guessoum A.,
Berkani, D., 2007. Error Propagation Analysis of Fast
Recursive Least Squares Algorithms. Proc. 9th
IASTED International Conference on Signal and
Image Processing, Honolulu, Hawaii, USA, August
20–22, pp.97-101.
Benallal, A., Gilloire, A., 1988. A New method to stabilize
fast RLS algorithms based on a first-order model of
the propagation of numerical errors. Proc. ICASSP,
New York, USA, pp.1365-1368
Benallal, A., Benkrid, A., 2007. A simplified FTF-type
algorithm for adaptive filtering. Signal processing,
vol.87, no.5, pp.904-917.
Cioffi, J., Kailath, T., 1984. Fast RLS Transversal Filters
for adaptive filtering. IEEE press. On ASSP, vol.32,
no.2, pp.304-337.
Gilloire, A., Moulines, E., Slock, D., Duhamel, P., 1996.
State of art in echo cancellation. In A.R. Figuers-vidal,
Digital Signal processing in telecommunication,
Springer, Berlin, pp.45–91
Haykin, S., 2002. Adaptive Filter Theory, Prentice-Hall.
NJ, 4
th
edition.
Macchi, O., 1995. The Least Mean Squares Approach with
Applications in Transmission, Wiley. New York.
Mavridis, P.P., Moustakides, G.V., 1996. Simplified
Newton-Type Adaptive Estimation Algorithms. IEEE
Trans. Signal Process, vol.44, no.8.
Moustakides, G.V., Theodoridis, S., 1999. Fast Newton
transversal filters - A new class of adaptive estimation
algorithms. IEEE Trans. Signal Process, vol.39, no.10,
pp.2184–2193.
Sayed, A.H., 2003. Fundamentals of Adaptive Filtering,
John Wiley & Sons. NJ,
Slock, D.T.M., Kailath, T., 1991. Numerically stable fast
transversal filters for recursive least squares adaptive
filtering,” IEEE transactions on signal processing,
vol.39, no.1, pp.92-114.
Slock, D.T.M., 1993. On the convergence behaviour of the
LMS and the NLMS algorithms. IEEE Trans. Signal
Processing, vol.42, pp.2811-2825.
Treichler, J.R., Johnson, C.R., Larimore, M.G., 2001.
Theory and Design of Adaptive Filter, Prentice Hall,
IMPROVEMENT OF THE SIMPLIFIED FTF-TYPE ALGORITHM
161
