
APPROXIMATION OF 5-LIMIT JUST INTONATION
Computer MIDI Modeling in Negative Systems of Equal Divisions of the Octave
Mykhaylo Khramov
Independent researcher, 53-2, Plekhanova street, 91005, Lugansk, Ukraine
Keywords: Intonation, just, music, score, tuning.
Abstract: The article matter is related with music processing by MIDI protocol during computer modeling of fixed
scales with non-traditional equal temperaments. Are touched negative temperaments, which based on closed
series of fifths, compressed relative conventional tuning. Is marked, that such systems, can better approach
to just intonation. They give sensation out of tuning during listening to music performed by scores with
mistaken using of accidentals, which inaccessible in a conventional temperament system. Is given a
subprogram example of the automatic Pitch Bend change in MIDI protocol for modeling of negative system
of equal divisions of the octave.
1 INTRODUCTION
1.1 Purpose of the Paper
Author imparts about applying of negative systems
of equal divisions of the octave and how they was
obtained by means of MIDI protocol.
1.2 5-limit Just Intonation (5LJI) and
Natural Scale (NS)
5LJI is an ideal infinite graded system of fixed
tuning which provide:
1. for all pairs of grades, correlation of sound
frequencies between grades of each pair with
rational number factorable to primes no more 5
by value;
2. for each grade existence of all other grades,
with anyone ratios of frequencies, which
satisfy the condition 1.
Everywhere in this paper a music which allow
5LJI is supposed. Compositions by J. S. Bach can be
such examples (Asmussen, 2001).
NS is a set of sounds of defined frequencies with
correlations, which proper to natural numbers.
Frequency of the 1-st element of NS is lowest, 2-nd
in 2 times higher of lowest, 3-rd in 3 times higher of
lowest, and so on.
In 5LJI is possible to build not full NS from any
grade. In such ones there will be no elements with
numbers which contain prime factors more 5 by
value. Numbers 7, 11, 13, 14, … will be absent.
1.3 System of Equal Divisions of the
Octave (EDO), Evaluations and
Initial Values
The EDO system is graded finite fixed tuning
ensuring:
1. for each grade possbility or existence of other
grades, with interval of a perfect octave up
and/or down;
2. for all intervals of a perfect octave existence
of an identical quantity of grades inside each
octave;
3. for all pairs of an identical interval between
grades of each pair.
Conventional 12EDO system has so called
semitone between adjacent grades. 1/100 of
semitone named cent, is adopted as a basis of
evaluations in this paper. The values cited without
verifying calculations, are obtained in the software
Scala (Op de Coul, 2004).
1.4 Negative EDO System
R. H. M. Bosanquet has offered a method of
deriving of other EDO systems from an accepted for
initial system 12EDO (E. T. at Bosanquet):
«…Let a regular system of fifths start from c. If they
181
Khramov M. (2008).
APPROXIMATION OF 5-LIMIT JUST INTONATION - Computer MIDI Modeling in Negative Systems of Equal Divisions of the Octave.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 181-184
DOI: 10.5220/0001932001810184
Copyright
c
SciTePress
are positive, then at each step the pitch rises further
from E. T. It can only return to c by sharpening an E.
T. note.
Suppose that b is sharpened one E. T. semitone,
so as to become c; then the return may be effected at
the first; b in 5 fifths, at the second b in 17 fifths, at
the third b in 29 fifths; and so on. Thus we obtain the
primary positive systems…
If the fifths are negative, the return may be
effected by depressing c# a semitone in 7, 19, 31...
fifths; we thus obtain the primary negative
systems…» (Bosanquet, 1875)
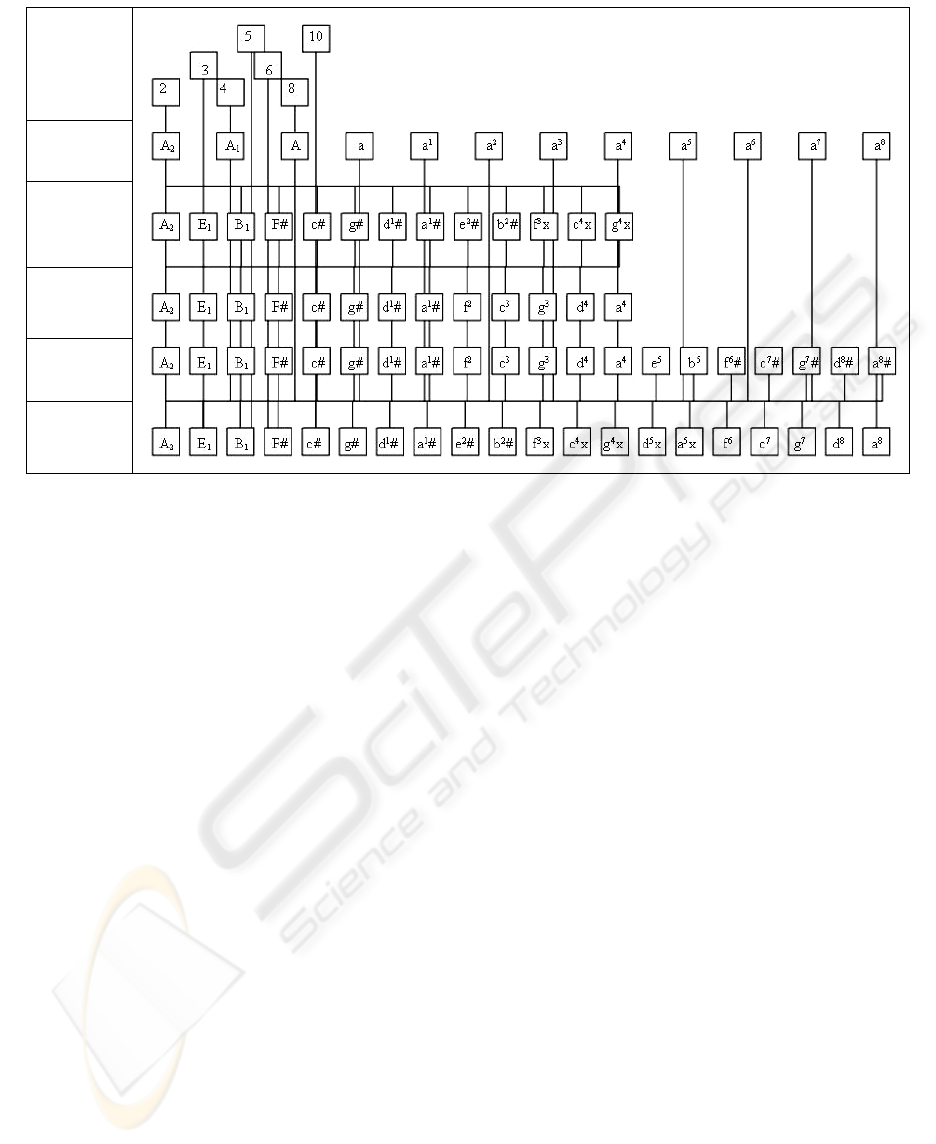
The Figure 1 illustrates application of this
method from note A
2
as origin.
Initial system is created by uniform compressing
of a series of 12 perfect fifths with a small interval,
which is known as comma of Pythagoras (CP). In a
scale of Pythagoras (SP) are used fifths absolutely
coincident with interval between 2-nd and 3-rd
elements of NS or perfect fifth.
The octave of all EDO systems is exactly equal
to an interval between 2-nd and 4-th elements of NS
or perfect octave. 12 fifths of SP exceed 7 octaves
on CP by size 23.46 cent.
Uniform compression of all 12 fifths SP with the
goal to eliminate CP gives 12 fifths of the most
spreaded 12EDO system. A fifth of this system
approximates perfect fifth with an error -1.955 cent,
and is adopted as initial for a further building.
19 fifths of a 12EDO system exceed 11 octaves
by one semitone of a 12EDO system. After uniform
compression (for elimination of this semitone) all 19
fifths of a 12EDO system, are obtained 19 fifths of a
19EDO system.
A fifth of 19EDO system has departure -5.263
cent from an initial value and approximates perfect
one with an error -7.218 cent.
A fifth of the next after 19EDO negative 31EDO
system approximates perfect one with an error -
5.181 cent.
The useful paradox of negative EDO systems:
the impairment of approximation of perfect fifth of
an initial 12EDO system, may automatically
improve approximation of major third of 5LJI
(interval between 8-th and 10-th elements of NS on
Figure 1).
«… For if we take 4 negative fifths up, we have a
third with negative departure (-4δ) which can
approximately represent the departure of the perfect
third. Thus c# is either the third to a, or four fifths
up from a, in accordance with the usage of
musicians…» (Bosanquet, 1875).
1.5 Approximation 5LJI in 19/31EDO
Systems and Simplicity of
Transposing of Music, from 12EDO
System to Them
The attractiveness of such approximation becomes
noticeable from a Table 1.
Natural
Scale of
5LJI
Octave
Scale
12 Fifts
of Pyhago-
rean Scale
12 Fifths of
12EDO
System
19 Fifths of
12EDO
System
19 Fifths of
19EDO
System
Figure 1: Scheme of Building of 19EDO System from Note A of Subcontraoctave (A
2
) as Origin.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
182

19EDO system is less preferable, as in
polyphony of instruments, rich by upper overtones
(harpsichord, piano), it can give noticeable sensation
out of tuning. It can not arise in same system, for
timbres of flute for example. The most probable
reason of it, is in a too large error of perfect fifth.
The Table 2 demonstrates simplicity of the
correspondences between all possible designations
of the notes and numbers of grades of these systems.
In it the accidental n indicates a lack or cancellation
of operation of other ones, i. e. neutral pitch of the
note.
Application of additional accidentals actually is
not required and direct using of scores for 12EDO
system is possible for playing in 19/31EDO ones.
2 SUBJECT OF RESEARCH
2.1 Possibility of Computer Modeling
of 19/31EDO Systems
Practically each modern computer has a sound
synthesizer, supporting protocol MIDI. Such
synthesizer has a set of channels.
Each channel is polyphony 12EDO system with
independent control, providing changed Pitch Bend
(PB).
PB works similarly to accidental, but shifts
pitches of all notes in the channel, as sounding, as
well consequent. Therefore its application for
retuning of the musical pieces from a 12EDO system
to other ones, requires in each channel only one
voice. A polyphony in each channel also is possible,
but the octaves and unisons only are admissible
between voices.
Any grades of 19EDO and 31EDO systems can
be obtained from suited 12EDO grades equipped by
an appropriate PB value from the Table 2.
PB value for each note can be added to software
Sibelius 4 (Eastwood and Others, 2005), allowing to
transpose conventional scores to MIDI versions:
//(c)Mykhaylo Y. Khramov, 2006
switch (NameOfNote)
{
case ("Gx"){PB = "-48¢~B 66,48";}
case ("G#"){PB = "-26¢~B 95,55";}
case ("Gn"){PB = "-3¢~B 124,62";}
case ("Gb"){PB = "+19¢~B 25,70";}
case ("Gbb"){PB = "+42¢~B 54,77";}
:
Table 1: Comparison of Three Variants of 5LJI Approximation by EDO systems.
5LJI Approximation
NS 12EDO 19EDO 31EDO
Cents Cents Cents
System
Interval
El-ts Cents
Size Abs. error Size Abs. error Size Abs. error
Major Third 10/8 386.314 400.000 13.686 378.947 7.367 387.096 0.782
Perfect Fifth 3/2 701.955 700.000 1.955 694.737 7.218 696.774 5.181
Octave 4/2 1200.000 1200.000 0.000 1200.000 0.000 1200.000 0.000
The average absolute error of approximation 5.214
4.862
1.988
Table 2: Modeling of 19EDO and 31EDO Systems by Evaluation for All Possible Notes of PB of Protocol MIDI.
Note Designation System Grade from Origin at Cn
12EDO, initial 19EDO 31EDO
Cents Cents
Name Accidental
Number PB
Cents
(Pitch)
PB
Depart. Pitch
Number PB
Depart. Pitch
Number
x 9 8192 900.000 4959 -78.947 821.053 13 6210 -48.387 851.613 22
# 8 8192 800.000 6467 -42.105 757.895 12 7135 -25.806 774.194 20
n 7 8192 700.000 7976 -5.263 694.737 11 8060 -3.226 696.774 18
b 6 8192 600.000 9485 31.579 631.579 10 8985 19.355 619.355 16
G
bb 5 8192 500.000 10994 68.421 568.421 9 9910 41.935 541.935 14
:
: : : : : : : : : : : :
x 11 8192 1100.000 4527 -89.474 1010.526 16 5946 -54.839 1045.161 27
# 10 8192 1000.000 6036 -52.632 947.368 15 6871 -32.258 967.742 25
n 9 8192 900.000 7545 -15.789 884.211 14 7796 -9.677 890.323 23
b 8 8192 800.000 9054 21.053 821.053 13 8720 12.903 812.903 21
A
bb 7 8192 700.000 10563 57.895 757.895 12 9645 35.484 735.484 19
APPROXIMATION OF 5-LIMIT JUST INTONATION - Computer MIDI Modeling in Negative Systems of Equal
Divisions of the Octave
183

Figure 2: Prepared MIDI Version of Score.
case ("Ax"){PB = "-55¢~B 58,46";}
case ("A#"){PB = "-32¢~B 87,53";}
case ("An"){PB = "-10¢~B 116,60";}
case ("Ab"){PB = "+13¢~B 17,68";}
case ("Abb"){PB = "+35¢~B 45,75";}
default {PB = "±00¢~B 0,64";}
}
return PB;
Such simple subprogram allows to retune
automatically the musical pieces and to get audible
models of their sounding. Some from them are freely
offered for listening to and discussion (Khramov,
2004, 2006).
On Figure 2, the subprogram has added above
each note in ossias the text, which is seen from an
initial quotation marks up to a tilde, and is hidden,
since a tilde and up to a completing quotation marks.
The visible text shows to observer the departure of
each note pitch, and hidden one transmits
appropriate PB to a MIDI device. It calls a required
departure of each note pitch for a selected 31EDO
2.2 Modeling of Negative Systems,
Indicates Mistakes in Scores
If in a context 12EDO major third A-C# for example
is in score mistakenly designated as A-Db, the
playing by this score in 31EDO will cause obvious
sensation out of tuning, completely inaccessible
during the playing in a system 12EDO. The
respelling of mistakenly notation removes sensation
out of tuning also during the playing in 31EDO.
The verification of scores by hearing plays the
important role in the process of transposing of
12EDO scores for the performance of them in
positive by Bosanquet (22EDO, 53EDO) systems
(Khramov, 2008).
REFERENCES
Asmussen, R., 2001. Periodicity of sinusoidal frequencies
as a basis for the analysis of Baroque and Classical
harmony: a computer based study. The University of
Leeds. School of Music.
http://www.terraworld.net/c-jasmussen/
Bosanquet, R. H. M., 1875. On the theory of the division
of the octave. In Proceedings of the Royal Society. No.
161. http://geocities.com/kmy180753/downloads/
EnhrmArticleOfBosnquet.pdf, http://geocities.com/
kmy180753/downloads/EnhrmArticleOfBosnquet.doc
Op de Coul, M., 2004. Scala Software. Netherlands,
version 2.2p. http://www.xs4all.nl/~huygensf/scala
Eastwood, M., Spreadbury, D., Finn, B., Finn, J., 2005.
Sibelius 4. Reference. http://www.sibelius.com/buy
Khramov, M., 2004. My music. From http://
members.sibeliusmusic.com/commator
Khramov, M., 2006. Another tuning. Audio CD. http://
geocities.com/commator/CDPages/AnotherTuning.htm
Khramov, M., 2008. Project Commator and Sonantometry.
In Proceedings of the FRSM-2008 International
Symposium Frontiers of Research on Speech and
Music. Jadavpur University, Kolkata.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
184
